Greatest element and least element

수학(mathematic), 특히 순서 이론(order theory)에서, 부분적으로 순서화된 집합(partially ordered set, 포셋(poset))의 부분집합 $S$ 의 최대 원소(greatest element)는 $S$ 의 모든 각 다른 원소보다 큰 $S$ 의 원소입니다. 용어 최소 원소(least element)는 이중적(dually)으로 정의됩니다. 즉, 그것은 $S$ 의 모든 각 다른 원소보다 작은 $S.$ 의 원소입니다.

Definitions

$(P,\leq )$ 를 준순서화된 집합(preordered set)이라고 놓고 $S\subseteq P$ 라고 놓습니다. 원소 $g\in P$ 는 만약 $g\in S$ 이고 다음을 만족시키면 $S$ 의 최대 원소(greatest element of $S$ )라고 말합니다:

s\leq g

for all

s\in S.

위의 정의에서 $\,\leq \,$ 대신 $\,\geq \,$ 를 사용함으로써, $S$ 의 최소 원소의 정의가 얻습니다. 명시적으로, 원소 $l\in P$ 는 만약 $l\in S$ 이고 그것이 다음을 만족시키면 $S$ 의 최소 원소(least element of $S$ )라고 말합니다:

l\leq s

for all

s\in S.

만약 $(P,\leq )$ 는 심지어 부분적으로 순서화된 집합(partially ordered set)이면, $S$ 는 많아야 하나의 최대 원소를 가질 수 있고 많아야 하나의 최소 원소를 가질 수 있습니다. $S$ 의 최대 원소가 존재하고 고유할 때마다, 이 원소는 $S$ 의 그 최대 원소라고 불립니다. 용어 $S$ 의 그 최소 원소는 유사하게 정의됩니다.

만약 $(P,\leq )$ 가 최대 원소 (각각, 최소 원소)를 가지면 이 원소는 $(P,\leq )$ 의 꼭대기(top) (각각, 밑바닥(bottom))이라고도 불립니다.

Relationship to upper/lower bounds

최대 원소는 위쪽 경계(upper bounds)와 밀접하게 관련되어 있습니다.

$(P,\leq )$ 를 준순서화된 집합(preordered set)이라고 놓고 $S\subseteq P$ 라고 놓습니다. $(P,\leq )$ 에서 $S$ 의 위쪽 경계(upper bounds)는 $u\in P$ 이고 모든 $s\in S$ 에 대해 $s\leq u$ 임을 만족하는 원소 $u$ 입니다. 중요하게, $P$ 에서 $S$ 의 위쪽 경계는 $S$ 의 원소일 필요는 없다는 것입니다.

만약 $g\in P$ 이면 $g$ 가 $S$ 의 최대 원소인 것과 $g$ 가 $(P,\leq )$ 에서 $S$ 의 위쪽 경계이고 $g\in S$ 인 것은 필요충분 조건입니다. 특히, $S$ 의 임의의 최대 원소는 ( $P$ 에서) $S$ 의 위쪽 경계이기도 하지만 $P$ 에서 $S$ 의 위쪽 경계는 $S$ 의 최대 원소인 것과 그것이 $S$ 에 속하는 것은 필요충분 조건입니다. $P=S$ 인 특별한 경우에서, " $u$ 는 $S$ 에서 $S$ 의 위쪽 경계이다"라는 정의는 다음과 같이 됩니다: $u$ 는 $u\in S$ 이고 모든 $s\in S$ 에 대해 $s\in S,$ 임을 만족하는 원소이며, 이는 이전에 주어진 최대 원소의 정의와 완전하게 동일합니다. 따라서 $g$ 가 $S$ 의 최대 원소인 것과 $g$ 가 $S$ 에서 $S$ 의 위쪽 경계인 것은 필요충분 조건입니다.

만약 $u$ 가 $S$ 에서 $S$ 의 위쪽 경계가 아닌 $P$ 에서 $S$ 의 위쪽 경계이면 (이것이 발생하는 것과 $u\not \in S$ 인 것은 필요충분 조건), $u$ 는 $S$ 의 최대 원소가 될 수 없습니다 (어쨌든, 어떤 다른 원소가 $S$ 의 최대 원소일 가능성이 있습니다). 특히, $S$ 가 동시에 최대 원소를 가지지 않고 $P$ 에서 $S$ 의 위쪽 경계가 존재하는 것이 가능합니다.

심지어 집합이 일부 위쪽 경계를 가지더라도, 음의 실수의 예제에서 볼 수 있듯이 최대 원소를 가질 필요는 없습니다. 이 예제는 역시 최소 위쪽 경계 (이 경우 숫자 0)의 존재가 최대 원소의 존재를 의미하지 않는다는 것을 보여줍니다.

Contrast to maximal elements and local/absolute maximums

준순서화된 집합의 부분집합의 최대 원소는 집합에서 임의의 다른 원소보다 엄격하게 작지 않은 원소인 집합의 최대한의 원소(maximal element)와 혼동해서는 안 됩니다.

$(P,\leq )$ 를 준순서화된 집합(preordered set)이라고 놓고 $S\subseteq P$ 라고 놓습니다. 원소 $m\in S$ 은 만약 다음 조건이 만족되면 $S$ 의 최대한의 원소(maximal element of $S$ )라고 말합니다:

s\in S

가

m\leq s

를 만족시킬 때마다, 반드시

s\leq m

이다.

만약 $(P,\leq )$ 가 부분적으로 순서화된 집합(partially ordered set)이면, $m\in S$ 은 $S$ 의 최대한의 원소인 것과 $m\leq s$ 이고 $s\neq m$ 임을 만족하는 임의의 $s\in S$ 가 존재하지 않는 것은 필요충분 조건입니다. $(P,\leq )$ 의 최대한의 원소(maximal element of $(P,\leq )$ )는 부분집합 $S:=P$ 의 최대한의 원소를 의미하는 것으로 정의됩니다.

집합은 최대 원소 없이 여러 개의 최대한의 원소를 가질 수 있습니다. 위쪽 경계 및 최대한의 원소와 마찬가지로, 최대 원소가 존재하지 않을 수 있습니다.

전체적으로 순서화된 집합(totally ordered set)에서, 최대한의 원소와 최대 원소는 일치합니다; 그리고 그것은 역시 최댓값(maximum)이라고도 불립니다; 함수 값의 경우에서, 그것은 역시 지역적 최댓값(local maximum)과의 혼동을 피하기 위해 절대 최댓값(absolute maximum)이라고도 불립니다.^[1] 이중 용어는 최솟값(minimum)과 절대 최솟값(absolute minimum)입니다. 함께 그것들은 절대 극단값(absolute extrema)이라고 불립니다. 유사한 결론이 최소 원소에 대해 유지됩니다.

Role of (in)comparability in distinguishing greatest vs. maximal elements

준순서화된 집합 $(P,\leq )$ 의 최대 원소 $g$ 와 최대한의 원소 $m$ 사이의 가장 중요한 차이점 중 하나는 비교할 수 있는 원소와 관련이 있습니다. 두 원소 $x,y\in P$ 는 $x\leq y$ 또는 $y\leq x$ 이면 비교-가능(comparable)이라고 말합니다; 그것들은 만약 비교-가능이 아니면 비-비교가능(incomparable)이라고 불립니다. 준순서가 반사적(reflexive)이기 때문에 (이는 $x\leq x$ 가 모든 원소 $x$ 에 대해 참임을 의미함), 모든 각 원소 $x$ 는 항상 자신과 비교-가능입니다. 결과적으로, 비-비교가능이 될 수 있는 유일한 원소의 쌍은 구별되는(distinct) 쌍입니다. 일반적으로, 어쨌든, 준순서화된 집합 (및 심지어 방향화된 부분적으로 순서화된 집합)은 비-비교가능인 원소를 가질 수 있습니다.

정의에 의해, 원소 $g\in P$ 는 만약 모든 각 $s\in P$ 에 대해 $s\leq g$ 이면 $(P,\leq )$ 의 최대 원소입니다; 따라서 그 정의에 따라, $(P,\leq )$ 의 최대 원소는, 특히, $P$ 에서 모든 각 원소와 비교-가능이 되어야 합니다. 이것은 최대한의 원소에 요구되지 않습니다. $(P,\leq )$ 의 최대한의 원소는 $P$ 에서 모든 각 원소와 비교-가능이 됨을 요구하지 않습니다. 이것은 "최대 원소"의 정의와 달리, "최대한의 원소"의 정의는 중요한 if 문을 포함하고 있기 때문입니다. $m\in P$ 에 대해 $(P,\leq )$ 의 최대한의 원소가 되어야 하는 정의하는 조건은 다음과 같이 다시 바꿀 수 있습니다:

s\in P

에 대해, 만약

m\leq s

(따라서

m

과 비-비교가능인 원소는 무시됨)이면

s\leq m

입니다.

Example where all elements are maximal but none are greatest

$S$ 가 적어도 두 개의 (구별되는) 원소를 포함하는 집합이고 $i\leq j$ 인 것과 $i=j$ 인 것이 필요충분 조건이라고 선언함으로써 $S$ 위의 부분 순서 $\,\leq \,$ 를 정의한다고 가정합니다. 만약 $i\neq j$ 가 $S$ 에 속하면 $i\leq j$ 도 $j\leq i$ 도 유지되지 않으며, 이는 $S$ 에서 모든 구별되는 (즉, 같지 않은) 원소의 쌍이 비-비교가능임을 보여줍니다. 결과적으로, $(S,\leq )$ 는 최대 원소를 가질 수 없습니다 (왜냐하면 $S$ 의 최대 원소가, 특히, $S$ 의 모든 각 원소와 비교-가능이어야 하지만 $S$ 는 그러한 원소를 가지지 않기 때문입니다). 어쨌든, 모든 각 원소 $m\in S$ 는 $(S,\leq )$ 의 최대한의 원소인데 왜냐하면 $S$ 에서 $m$ 및 $\geq m$ 과 비교-가능 둘 다인 정확하게 하나의 원소가 있고, 해당 원소는 $m$ 자체 (물론 $\leq m$ 임)이기 때문입니다.^{[note 1]}

대조적으로, 만약 준순서화된 집합(preordered set) $(P,\leq )$ 이 우연히 최대 원소 $g$ 를 가지게 되면 $g$ 는 반드시 $(P,\leq )$ 의 최대한의 원소가 될 것이고 더욱이, 최대 원소 $g$ 의 결론이 $P$ 의 모든 각 원소와 비교-가능이라는 것이기 때문에, 만약 $(P,\leq )$ 도 부분적으로 순서화되면 $g$ 가 $(P,\leq )$ 의 유일한 최대한의 원소라는 결론을 내릴 수 있습니다. 어쨌든, 고유성의 결론은 만약 준순서화된 집합 $(P,\leq )$ 도 부분적으로 순서화되지 않으면 더 이상 보장되지 않습니다. 예를 들어, $R$ 이 비-빈 집합이고 $i\leq j$ 가 항상 모든 $i,j\in R$ 에 대해 성립한다고 선언함으로써 $R$ 위에 준순서 $\,\leq \,$ 를 정의한다고 가정합니다. 방향화된 준순서화된 집합 $(R,\leq )$ 이 부분적으로 순서화된 것과 $R$ 이 정확하게 하나의 원소를 가지는 것은 필요충분 조건입니다. $R$ 로부터 모든 원소의 쌍은 비교-가능이고 $R$ 의 모든 각 원소는 $(R,\leq )$ 의 최대 원소 (및 따라서 역시 최대한의 원소)입니다. 따라서 특히, 만약 $R$ 이 적어도 두 개의 원소를 가지면 $(R,\leq )$ 은 여러 개의 구별되는 최대 원소를 가집니다.

Properties

전체에 걸쳐, $(P,\leq )$ 를 부분적으로 순서화된 집합(partially ordered set)으로 놓고 $S\subseteq P$ 라고 놓습니다.

집합 $S$ 는 많아야 하나의 최대 원소를 가질 수 있습니다.^{[note 2]} 따라서 만약 집합이 최대 원소를 가지면 그것은 반드시 고유합니다.
만약 그것이 존재하면, $S$ 의 최대 원소는 $S$ 에도 포함된 $S$ 의 위쪽 경계(upper bound)입니다.
만약 $g$ $g$ 가 $S$ $S$ 의 최대 원소이면 $g$ $g$ 는 역시 $S$ $S$ 의 최대한의 원소이고^{[note 3]} 게다가, $S$ $S$ 의 임의의 다른 최대한의 원소는 반드시 $g.$ $g.$ 와 같을 것입니다.^{[note 4]}
- 따라서 집합 $S$ 가 여러 개의 최대한의 원소를 가지면 그것은 최대 원소를 가질 수 없습니다.
만약 $P$ 가 오름 체인 조건(ascending chain condition)을 만족시키면, $P$ 의 부분집합 $S$ 가 최대 원소를 가지는 것과 그것이 하나의 최대한의 원소를 가지는 것은 필요충분 조건입니다.^{[note 5]}
$S$ $S$ 에 대한 $\,\leq \,$ $\,\leq \,$ 의 제한이 전체 순서일 때 (맨 위 그림에서 $S=\{1,2,4\}$ $S=\{1,2,4\}$ 가 예제임), 최대한의 원소와 최대 원소의 개념이 일치합니다.^{[note 6]}
- 어쨌든, 이것은 $S$ 가 최대 원소를 가질 때마다 위에서 언급한 것처럼 개념도 일치하기 때문에 필요 조건이 아닙니다.
만약 최대한의 원소와 최대 원소의 개념이 $P$ 의 모든 각 2-원소 부분집합 $S$ 에서 일치하면, $\,\leq \,$ 는 $P$ 의 전체 순서입니다.^{[note 7]}

Sufficient conditions

유한 체인(chain)에는 항상 가장 큰 원소와 가장 작은 원소가 있습니다.

Top and bottom

부분적으로 순서화된 전체 집합의 최소 원소와 최대 원소는 특별한 역할을 하고 각각 맨바닥(bottom, ⊥)과 꼭대기(top, ⊤), 또는 영(zero, 0)과 단위(unit, 1)라고도 불립니다. 만약 둘 다 존재하면, 그 포셋은 경계진 포셋(bounded poset)이라고 불립니다. 0과 1의 표기법은 포셋이 여집합된 격자(complemented lattice)일 때, 그리고 혼동이 없을 때, 즉 맨바닥과 꼭대기와 다른 원소 0과 1을 이미 포함하고 있는 숫자의 부분 순서에 대해 이야기하지 않을 때 바람직하게 사용됩니다. 최소 원소와 최대 원소의 존재는 부분 질서의 특별한 완비성 속성(completeness property)입니다.

추가 입문 정보는 순서 이론(order theory)에 대한 기사에서 찾을 수 있습니다.

Examples

정수(integers)의 부분집합은 실수(real numbers)의 집합 $\mathbb {R}$ 에서 위쪽 경계를 가지지 않습니다.
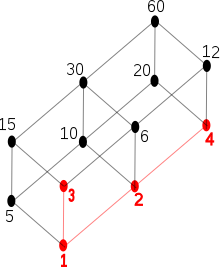
$\{a,b,c,d\}$ 위에 관계 $\,\leq \,$ 를 $a\leq c,$ $a\leq d,$ $b\leq c,$ $b\leq d$ 에 의해 주어졌다고 놓습니다. 집합 $\{a,b\}$ 는 위쪽 경계 $c$ 와 $d$ 를 가지지만, 최소 위쪽 경계를 가지지 않고, 최대 원소를 가지지 않습니다 (참조. 그림).
유리수(rational numbers)에서, 제곱이 2보다 작은 숫자의 집합은 위쪽 경계를 가지지만 최대 원소와 최소 위쪽 경계를 가지지 않습니다.
$\mathbb {R}$ 에서, 1보다 작은 숫자의 집합은 최소 위쪽 경계, 즉, 1을 가지지만, 최대 원소를 가지지 않습니다.
$\mathbb {R}$ 에서, 1보다 작거나 같은 숫자의 집합은 최대 원소, 즉, 1을 가지며, 이는 역시 최소 위쪽 경계입니다.
곱 순서(product order)를 갖는 $\mathbb {R} ^{2}$ 에서, $0<x<1$ 을 갖는 쌍 $(x,y)$ 의 집합은 위쪽 경계를 가지지 않습니다.
사전식 순서(lexicographical order)를 갖는 $\mathbb {R} ^{2}$ 에서, 이 집합은 위쪽 경계, 예를 들어, $(1,0)$ 을 가집니다. 그것은 최소 위쪽 경계를 가지지 않습니다.

Notes

^ Of course, in this particular example, there exists only one element in $S$ that is comparable to $m,$ which is necessarily $m$ itself, so the second condition "and $\geq m,$ " was redundant.
^ If $g_{1}$ and $g_{2}$ are both greatest, then $g_{1}\leq g_{2}$ and $g_{2}\leq g_{1},$ and hence $g_{1}=g_{2}$ by antisymmetry.
^ If $g$ is the greatest element of $S$ and $s\in S,$ then $s\leq g.$ By antisymmetry, this renders ( $g\leq s$ and $g\neq s$ ) impossible.
^ If $M$ is a maximal element, then $M\leq g$ since $g$ is greatest, hence $M=g$ since $M$ is maximal.
^ Only if: see above. — If: Assume for contradiction that $S$ has just one maximal element, $m,$ but no greatest element. Since $m$ is not greatest, some $s_{1}\in S$ must exist that is incomparable to $m.$ Hence $s_{1}\in S$ cannot be maximal, that is, $s_{1}<s_{2}$ must hold for some $s_{2}\in S.$ The latter must be incomparable to $m,$ too, since $m<s_{2}$ contradicts $m$ 's maximality while $s_{2}\leq m$ contradicts the incomparability of $m$ and $s_{1}.$ Repeating this argument, an infinite ascending chain $s_{1}<s_{2}<\cdots <s_{n}<\cdots$ can be found (such that each $s_{i}$ is incomparable to $m$ and not maximal). This contradicts the ascending chain condition.
^ Let $m\in S$ be a maximal element, for any $s\in S$ either $s\leq m$ or $m\leq s.$ In the second case, the definition of maximal element requires that $m=s,$ so it follows that $s\leq m.$ In other words, $m$ is a greatest element.
^ If $a,b\in P$ were incomparable, then $S=\{a,b\}$ would have two maximal, but no greatest element, contradicting the coincidence.