Confidence interval

Original article: w:Confidence interval

통계학(statistics)에서, 신뢰 구간(confidence interval, 줄여서 CI)은 관측된 데이터의 통계량으로부터 계산된 추정(estimate)의 유형입니다. 이것은 미지수 매개-변수(parameter) (예를 들어, 평균)에 대해 그럴듯한 값의 범위의 제안입니다. 구간은 참 매개-변수가 제안된 범위 안에 있다는 결합된 신뢰 수준을 가집니다. 관측 $x_{1},\ldots ,x_{n}$ 및 신뢰 수준 $\gamma$이 주어지면, 유효한 신뢰 구간은 참 놓여-있는 매개-변수를 포함하는 $\gamma$ 확률을 가집니다. 신뢰의 수준은 조사자에 의해 선택될 수 있습니다. 일반 용어에서, 미지수 매개-변수에 대해 신뢰 구간은 해당하는 추정기(estimator)의 분포(distribution)를 표본화하는 것에 기초됩니다.

보다 엄격하게 말해서, 신뢰 수준은 미지수 모집단 매개-변수의 참 값을 포함하는 가능한 신뢰 구간의 빈도(frequency) (즉, 비율)를 나타냅니다. 다시 말해서, 만약 신뢰 구간이 독립 표본 통계량의 무한 숫자로부터 주어진 신뢰 수준을 사용하여 구성되면, 매개-변수의 참 값을 포함하는 그들 구간의 비율은 신뢰 수준과 같을 것입니다. 예를 들어, 만약 신뢰 수준 (CL)이 90%이면 가상의 명확하지 않은 데이터 모음에서, 표본의 90%에서 구간 추정은 모집단 매개-변수를 포함할 것입니다.

신뢰 수준은 데이터를 검사하기 전에 지정됩니다. 가장 공통적으로, 95% 신뢰 수준이 사용됩니다. 어쨌든, 90%와 99%의 신뢰 수준은 역시 종종 분석에서 사용됩니다.

신뢰 구간의 폭에 영향을 미치는 요인은 표본의 크기, 신뢰 수준, 및 표본에서 변동가능성을 포함합니다. 더 큰 표본은, 다른 모든 요인이 같을 때, 모집단 매개-변수의 더 좋은 추정을 생성하기 위한 경향일 것입니다. 더 높은 신뢰 수준은 더 넓은 신뢰 구간을 생성하기 위한 경향일 것입니다.

많은 신뢰 구간은 형식: $(t-c\sigma _{T},t+c\sigma _{T})$의 것이며, 여기서 $t$는 데이터-집합의 실현이고, $c$는 상수이고 $\sigma _{T}$는 데이터-집합의 표준 편차입니다. 신뢰 구간의 형식을 표현하는 또 다른 방법:

(점 추정 – 오차 경계, 점 추정 + 오차 경계)

           또는 기호적으로 표현해서, (–EBM, +EBM)

여기서 (점 추정)은 m (모집단 평균)에 대해 추정으로 수행되고 EBM은 모집단 평균에 대해 오차 경계입니다.

오차의 한계 (EBM)은 신뢰 수준에 의존합니다.

철저하고, 일반적인 정의:

데이터-집합 $x_{1},\ldots ,x_{n}$이 확률 변수 $X_{1},\ldots ,X_{n}$의 구현으로 주어지며, 모델화된 것으로 가정합니다. $\theta$를 관심의 매개-변수로 놓고, $\gamma$를 1과 0 사이의 숫자로 놓습니다. 만약 $\theta$의 모든 각 값에 대해 $P(L_{n}<\theta <U_{n})=\gamma$를 만족하는 표본 통계량 $L_{n}=g(X_{1},\ldots ,X_{n})$ 및 $U_{n}=h(X_{1},\ldots ,X_{n})$이 존재하면, $(l_{n},u_{n})$은, 여기서 $l_{n}=g(x_{1},\ldots ,x_{n})$ 및 $u_{n}=h(x_{1},\ldots ,x_{n})$이며, $\theta$에 대해 $\gamma \times 100$% 신뢰 구간으로 불립니다. 숫자 $\gamma$는 신뢰 수준으로 불립니다.

Conceptual basis

In this bar chart, the top ends of the brown bars indicate observed means and the red line segments ("error bars") represent the confidence intervals around them. Although the error bars are shown as symmetric around the means, that is not always the case. It is also important to note that in most graphs, the error bars do not represent confidence intervals (e.g., they often represent standard errors or standard deviations)

Introduction

구간 추정(Interval estimation)은 점 추정(point estimation)과 대조될 수 있습니다. 점 추정은 관심 있는 즉, 어떤 양의 평균과 같은 모집단 매개-변수의 추정으로 주어진 단일 값입니다. 구간 추정은 매개-변수가 놓이는 것으로 추정되는 이내의 범위를 대신 지정합니다. 신뢰 구간은 공통적으로, 추정의 신뢰성(reliability)을 보이기 위해, 같은 매개-변수의 점 추정과 함께 테이블 또는 그래프로 보고됩니다.

예를 들어, 신뢰 구간은 조사 결과가 얼마나 신뢰할 수 있는지 설명하기 위해 사용될 수 있습니다. 선거–투표 여론의 선거인 명부에서, 그 결과가 응답자의 40%가 특정 정당에 투표할 의향이 있을 수 있습니다. 조사에 대한 같은 의향을 가진 전체 모집단에서 비율에 대해 99% 신뢰 구간은 30%에서 50%일 수 있습니다. 같은 데이터에서 우리는 90% 신뢰 구간을 계산할 수 있으며, 이 경우에서 37%에서 43%일 수 있습니다. 신뢰 구간의 길이를 결정하는 주요 요인은 평가 절차에 사용된 표본의 크기(size of the sample), 예를 들어 조사에서 부분을 취한 사람의 숫자입니다.

Meaning and interpretation

See also: § Practical example interpretation

신뢰 구간의 다양한 해석이 제공될 수 있습니다 (다음에서 예제로 90% 신뢰 구간을 사용합니다).

• 신뢰 구간은 표본(samples) (또는 반복된 표본(repeated samples))의 관점에서 표현될 수 있습니다: "이 절차는 수많은 표본에서 반복되어야 했지만, 참 모집단 매개-변수를 포함하는 (각 표본에 따라 다를 수 있는) 계산된 신뢰 구간의 분수는 90%를 향하는 경향일 것입니다."
• 신뢰 구간은 단일 표본의 관점에서 표현될 수 있습니다: "일부 미래 실험에서 계산된 신뢰 구간이 모집단 매개-변수의 참 값을 포함할 확률(probability)은 90%입니다." 이것은 모집단 매개-변수가 아닌 신뢰 구간에 대한 확률 명제임을 주목하십시오. 이것은 항목을 연구하기 위한 처리의 무작위 할당에 대한 논의가 이루어지는 것과 같은 맥락에서, 이전-실험 관점에서 신뢰 구간과 결합된 확률을 고려합니다. 여기서 실험자는 신뢰 구간을 계산하고, 실제 실험을하기 전에, 그들이 결국 계산하려고 하는 구간이 참이지만 미지수 값을 덮는 특별한 기회를 가짐을 알려고 있는 방법을 제시합니다. 이것은, 임의의 의미있는 의미로는 반복할 수 없는 표본화 절차의 가상적인 반복에 의존을 고려함에 의존하지 않는 것을 제외하고는, 위의 "반복된 표본" 해석과 매우 유사합니다. 네이만 구성(Neyman construction)을 참조하십시오.
• 신뢰 구간의 설명은 전체적으로 약간 다음과 같을 수 있습니다: "신뢰 구간은 매개-변수와 관측된 추정 사이의 차이가 10% 수준에서 통계적으로 중요하지(statistically significant) 않는 모집단 매개-변수에 대해 값을 나타냅니다." 실제로, 이것은 신뢰 구간이 구성될 수 있는 하나의 특정 방법에 관한 것입니다.

위의 각각에서, 다음 사항이 적용됩니다: 만약 매개-변수의 참 값이 90% 신뢰 구간 밖에 놓이면, 표본화 사건은 우연히 발생하는 10% (또는 보다 작게)의 확률로 발생한 것입니다 (즉, 최소한 참 매개-변수 값에서 멀리 떨어진 매개-변수의 점 추정을 얻습니다).

Misunderstandings

See also: § Counter-examples, and Misunderstandings of p-values

신뢰 구간과 수준은 꽤 자주 잘못 이해되고 있고, 발표된 연구는 심지어 전문 과학자도 종종 그들을 잘못 해석하는 것으로 보여 왔습니다.

• 95% 신뢰 수준은 주어진 실현된 구간에 대해 모집단 매개-변수가 구간 이내에 놓이는 확률이 95% (즉, 그 구간이 모집단 매개-변수를 덮는 95% 확률)라는 것을 의미하지는 않습니다. 엄격한 빈도주의 해석에 따르면, 한번 구간이 계산되면, 이 구간은 매개-변수를 덮거나 그렇지 않습니다; 그것은 더 이상 확률의 문제가 아닙니다. 95% 확률은 특정 계산된 구간이 아니라, 추정 절차의 신뢰성과 관련이 있습니다. 네이만 자신 (원래 신뢰 구간의 제안자)은 그의 원래 논문에서 이 점을 지적했습니다:

  "위의 설명에서 확률 명제는 통계학자가 미래에 관심을 가질 추정의 문제를 참조합니다. 사실, 나는 정확한 결과의 빈도가 α로 경향일 것임을 반복적으로 말해 왔습니다. 이제 표본이 이미 추출되었고, 그 계산이 [특정 한도]를 제공했다고 생각해 보십시오. 우리는 이 특별한 경우에서 [이들 한도 사이에 떨어지는] 참 값의 확률이 α와 같다고 말할 수 있습니까? 그 답은 분명하게 부정적입니다. 매개-변수는 미지수 상수이고, 그 값에 관련하는 확률 명제는 작성할 수 없을 것입니다..."

데보라 마요(Deborah Mayo)는 이것을 다음처럼 더 확장합니다:

"어쨌든, [데이터의] 값을 보았을 때, 네이만–피어슨 이론은 형성된 특정 신뢰 구간이 (1 − α)100% 확률 또는 (1 − α)100% 신뢰의 정도(신뢰도)와 함께 0의 참 값을 덮을 것이라는 결론을 내릴 수 없음을 강조해야 합니다. 자이던펠트(Seidenfeld)의 발언은 합법적으로 제공할 수 없는 어떤 것: 즉, 확률의 정도의 측정, 믿음, 또는 특정 구간 안에 놓이는 미지수 매개변수 값의 지원을 제공하기 위해 네이만–피어슨 신뢰 구간에 대한 (드물지 않은) 욕구에 뿌리를 둔 것으로 보입니다. 새비지(Savage, 1962)에 따르면, 매개 변수가 특정 구간 안에 놓일 확률은 최종 정밀도의 측정으로 참조될 수 있을 것입니다. 최종 정밀도의 측정이 바람직해 보일 수 있지만, 그리고 신뢰 수준은 종종 그러한 측정을 제공하는 것으로 (잘못) 해석되지만, 그러한 해석은 보증되지 않습니다. 일반적으로 인정하듯이, 그러한 오해는 단어 '신뢰'에 의해 장려됩니다."

• 95% 신뢰 수준이 표본 데이터의 95%가 신뢰 구간 이내에 놓인다는 것을 의미하지는 않습니다.
• 신뢰 구간은, 비록 모집단 매개-변수에 대해 그럴듯한 값의 추정으로 이해될 수 있을지라도, 표본 매개-변수에 대해 그럴듯한 값의 결정적인 범위는 아닙니다.
• 실험으로부터 계산된 95%의 특정 신뢰 수준이 이 구간 이내에 떨어지는 실험의 반복으로부터 표본 매개-변수의 95% 확률이 있음을 의미하지는 않습니다.

History

신뢰 구간은 1937년에 출판된 논문에서 예르지 네이만(Jerzy Neyman)에 의해 통계학에 도입되었습니다. 어쨌든, 신뢰 구간이 정확하고 일상적으로 사용되기 위해 꽤 오랜 시간이 걸렸습니다. 1959년에 다이켄과 화이트(Dyken and White)에 의해 출판된, 급성 뇌졸중에 대해 의학적 치료의 가장-초기의 현대 대조된 임상 시험에서, 연구원들은 코티솔이 뇌졸중의 위험을 증가시킨다고 결론지었습니다. 신뢰 구간이 적용되었을 때 어쨌든, 코티솔 제안을 사용하는 것이 가능한 이점이 없음은 엄격하게 참은 아님을 보여주었습니다. 코티솔이 위험을 감소시킬 12% 기회가 있었습니다. 특히 데이터-집합이 작을 수 있는 의학 분야에서, 신뢰 구간의 적절한 선택은 효과의 크기, 방향을 결정하는 것이 필요하고, 무 가설이 수용될 수 있는지 또는 거부될 수 있는지 여부를 확실하게 결정하기 위해 필요합니다.

1980년대까지는 저널은 논문에서 신뢰 구간과 p-값을 보고하는 것이 요구되지 않았습니다. 1992년까지, 부정확한 추정은 심지어 큰 시행에 대해서도 여전히 공통적이었습니다. 이것은 무 가설에 관련하여 명확한 결정을 방해했습니다. 예를 들어, 급성 뇌졸중에 대한 의학적 치료법에 대한 연구는 뇌졸중 치료가 사망률을 10%–20%만큼 감소 또는 증가시킬 수 있다는 결론에 도달했습니다. 그 연구에 대한 엄격한 입장은 예기치 못한 오류를 일으켜, 결론에 대한 불확실성을 더욱 증가시켰습니다. 연구는 지속되었고, 1997년까지 대규모 표본 풀과 허용-가능한 신뢰 구간을 갖는 시행은 결정적인 답: 코티솔 치료법은 급성 뇌졸중의 위험을 줄이지 않음이라는 것을 제공할 수 없었습니다.

Philosophical issues

신뢰 구간의 숨겨진 원리는 그들 자체가 무작위로 선택된 모집단의 부부-집합인 데이터에서 도출된 결과에서 고유의 불확실성을 처리하는 방법의 통계적 추론(statistical inference)에서 제기된 질문에 대한 답을 제공하기 위해 공식화되었습니다. 다른 답, 특히 신용 구간(credible intervals)의 형식에서 베이즈 추론(Bayesian inference)에 의해 제공되는 것이 있습니다. 신뢰 구간은 신뢰 경계를 결정하는 것에 대해 선택된 규칙에 해당하며, 여기서 이 규칙은 임의의 데이터가 획득되기 전에 또는 실험이 행해지기 전에 본질적으로 결정됩니다. 그 규칙은 얻어질 수 있는 모든 가능한 데이터-집합에 걸쳐, 규칙에 의해 결정된 구간이 고려 아래에서 양의 참 값을 포함할 높은 확률 ("높은"은 구체적으로 정량화됨)이 있음을 만족하는 것으로 정의됩니다. 베이즈 접근법은 "확률"의 해석을 베이즈 확률(Bayesian probability)로 수락에 따라, 주어진 데이터-집합으로부터 계산된 특정 구간이, 유용한 데이터 및 다른 정보에 조건부, 참 값을 포함할 특별한 확률을 가짐을 의미하는 것으로 해석될 수 있는 구간을 제공하는 것으로 보입니다. 신뢰 구간 접근법은 이것을 허용하지 않는데 왜냐하면 이 공식에서 및 이 같은 단계에서 구간의 경계와 참 값 둘 다가 고정된 값이고, 포함된 임의성이 없기 때문입니다. 다른 한편으로, 베이즈 접근법은 계산에 사용된 이전 확률만큼 오직 유효하지만, 신뢰 구간은 이전 확률에 대한 가정에 의존하지 않습니다.

추정에서 불확실성을 표현하는 구간이 공식화될 수 있는 방법과 그러한 구간이 해석될 수 있는 방법에 관련한 질문은 엄격하게 수학적인 문제가 되지 않고 철학적으로 문제가 있습니다. 수학은 '추론'에 대한 접근법의 기본 원칙이 확립되었으면 이를 인수할 수 있지만, 한 접근법이 또 다른 접근법보다 선호되어야 하는 이유를 말하는 오직 제한된 역할을 가집니다: 예를 들어, 95%의 신뢰 수준은 종종 생물 과학(biological sciences)에서 사용되지만, 이것은 관례 또는 중재의 문제입니다. 물리 과학(physical sciences)에서, 훨씬 더 높은 수준이 사용될 수 있습니다.

Relationship with other statistical topics

Statistical hypothesis testing

See also: Statistical hypothesis testing § Alternatives, and Estimation statistics

신뢰 구간은 통계적 중요성 테스트(significance testing)와 밀접하게 관련됩니다. 예를 들어, 만약 일부 추정된 매개-변수 θ에 대해 우리가 θ ≠ 0의 대안에 대비하여 θ = 0라는 무 가설(null hypothesis)을 테스트하기를 원한다면, 이 테스트는 θ에 대해 신뢰 구간이 0을 포함하는지 여부를 결정함으로써 수행될 수 있습니다.

보다 일반적으로, θ₀의 임의의 값에 대해 θ ≠ θ₀인 대안에 대비하여 무 가설 θ = θ₀를 테스트할 수 있는 가설 테스팅 절차의 유효성이 주어지면, 신뢰 수준 γ = 1 − α를 갖는 신뢰 구간은 해당하는 무 가설이 중요성 수준 α에서 거절되지 않는 임의의 숫자 θ₀를 포함하는 것으로 정의될 수 있습니다.

만약 두 매개-변수의 추정 (예를 들어, 두 독립 그룹 안의 변수의 평균값)이 겹치지 않는 신뢰 구간을 가지면, 두 값 사이의 차이는 α의 개별 값으로 표시되는 것보다 더 중요한(significant) 것입니다. 따라서, 이 "테스트"는 너무 보수적이고 α의 개별 값이 나타내는 것보다 더 중요한 결과를 초래할 수 있습니다. 만약 두 신뢰 구간이 겹쳐지면, 두 평균은 여전히 크게 다를 수 있습니다. 그에 따라서, 그리고 맨틀-헨젤(Mantel-Haenszel)와 일치하는, 카이-제곱된 테스트(Chi-squared test)는 우리는 비교하기 전에 두 평균에 대해 오차 경계에 ½ (0.707107)의 제곱근만큰 그것을 곱함으로써 줄이는 것에 의해 제안된 수정입니다.

신뢰 구간 개념과 계적 가설 테스팅(statistical hypothesis testing)의 개념의 공식화는 서로 다르지만, 그들은 어떤 의미에서 관련되고 어느 정도 보완적입니다. 모든 신뢰 구간이 이들 방법에서 구성되는 것은 아니지만, 신뢰 구간을 구성하는 한 가지 일반적인 목적 접근은 가설 θ = θ₀의 테스트는 100α%의 중요성 수준에서 거절되지 않는 모든 그들의 값 θ₀을 구성하기 위해 100(1 − α)% 신뢰 구간을 정의하는 것입니다. 그러한 접근법은 항상 이용-가능한 것은 아닌데 왜냐하면 적절한 중요성 테스트의 실제 유효성을 전제로 하기 때문입니다. 당연히, 중요성 테스트에 대해 요구되는 임의의 가정은 신뢰 구간으로 이월할 것입니다.

신뢰 구간 이내의 매개-변수 값이 가설 테스트에 의해 거절되지 않는 그들의 값과 동등하다는 일반적인 대응을 하는 것이 편리할 수 있지만, 이것은 위험할 수 있습니다. 많은 예제에서, 인용된 신뢰 구간은 오직 근사적으로 유효하며, 아마도 "더하기 또는 빼기 두 배의 표준 오차"에서 유도되고, 추정되는 해당하는 가설 테스트에 대해 이것의 의미는 보통 미지수입니다.

매개-변수에 대해 신뢰 구간이, 때때로 생각되는 것처럼, 이 매개-변수에 대해 테스트의 수락 영역과 같지 않다는 점에 주목할 가치가 있습니다. 신뢰 구간은 매개-변수 공간의 일부이며, 반면에 수락 영역은 표본 공간의 일부입니다. 같은 이유에 대해, 신뢰 수준은 중요성의 수준의 보완적인 확률과 같지 않습니다.

Confidence region

Main article: Confidence region

신뢰 영역(confidence region)은 여러 양을 처리하기 위해 신뢰 구간 개념을 일반화합니다. 그러한 영역은 아마도 표본화 오차(sampling error)의 정도를 나타낼 수 있을뿐만 아니라 (예를 들어) 만약 한 양에 대해 추정이 신뢰할 수 없으면, 다른 것은 역시 아마도 신뢰 할 수 없는지 여부를 역시 드러낼 수 있습니다.

Confidence band

Main article: Confidence band

신뢰 밴드(confidence band)은 통계적 분석(statistical analysis)에서 제한적이거나 잡음이 많은 데이터에 기반한 곡선 또는 함수의 추정에서 불확실성을 나타내기 위해 사용됩니다. 유사하게, 예측 밴드(prediction band)는 곡선 위의 새로운 데이터 점의 값에 대한 불확실성을 나타내기 위해 사용되지만, 노이즈에 영향을 받습니다. 신뢰 및 예측 밴드는 회귀 분석(regression analysis)의 결과의 그래픽 표현의 일부로 종종 사용됩니다.

신뢰 밴드는 신뢰 구간과 밀접한 관련되면, 이것은 단일 수치 값의 추정에서 불확실성을 나타냅니다. "신뢰 구간은, 구성에 의해, 단일 점을 오직 참조하므로, 그들은 여러 지점에서 동시에 유지되어야 하는 신뢰 구간보다 (이 점에서) 더 좁습니다."

Basic steps

이 예제는 표본이 정규 분포(normal distribution)에서 추출된 것으로 가정합니다. 모집단 평균에 대해 신뢰 구간을 계산하는 기본 절차는 다음과 같습니다:

1. 표본 평균, ${\bar {x}}$을 식별하십시오.

2. 모집단 표준 편차가 $\sigma$로 알려져 있는지, 또는, 미지수이고 표본 표준 편차 $s$에 의해 추정되는지 식별하십시오.

• 만약 모집단 표준 편차가 알려져 있으면 $z^{*}=\Phi ^{-1}\left(1-{\frac {\alpha }{2}}\right)=-\Phi ^{-1}\left({\frac {\alpha }{2}}\right)$이며, 여기서 $C=100(1-\alpha )\%$는 신뢰 수준이고 $\Phi$는 임계값으로 사용된 표준 정규 분포(standard normal distribution)의 CDF입니다. 이 값은 테스트에 대해 신뢰 수준에 오직 의존합니다. 전형적인 두 측면 신뢰 수준은 다음입니다:

C	z*
99%	2.576
98%	2.326
95%	1.96
90%	1.645

• 만약 모집단 표준 편차가 미지수이면 스튜던트의 t 분포(Student's t distribution)가 임계값으로 사용됩니다. 이 값은 테스트에 대해 신뢰 수준 (C)과 자유도에 의존합니다. 자유도는 관측의 숫자에서 일을 뺌으로써, n − 1로 구해집니다. 임계값은 t-분포 테이블에서 찾아집니다. 이 테이블에서 임계값은 $t^{*}=t_{\alpha }(r)$로 쓰이며, 여기서 $r$은 자유도이고 $\alpha ={1-C \over 2}$입니다.

3. 찾은 값을 적절한 방정식에 채우십시오:

• 알려진 표준 편차에 대해: $\left({\bar {x}}-z^{*}{\sigma \over {\sqrt {n}}},{\bar {x}}+z^{*}{\sigma \over {\sqrt {n}}}\right)$
• 미지수 표준 편차에 대해: $\left({\bar {x}}-t^{*}{s \over {\sqrt {n}}},{\bar {x}}+t^{*}{s \over {\sqrt {n}}}\right)$

Normal Distribution: graphical representation of confidence interval breakdown and relation of the confidence intervals to the z- and t-scores.

Significance of t-tables and z-tables

신뢰 구간은, 위의 기본 예제에서 보인 것처럼, 두 다른 값: t-값 또는 z-값을 사용하여 계산될 수 있습니다. 값 둘 다는 자유도 및 확률 분포의 꼬리를 기초하여 테이블에 정리되어 있습니다. 더 자주, z-값이 사용됩니다. 이것들은 오른쪽 꼬리 확률을 갖는 정규 분포의 임계값입니다. 어쨌든, t-값은 표본 크기가 30 미만이고 표준 편차가 미지수일 때 사용됩니다.

분산이 미지수일 때, 우리는 다른 추정기: $S_{n}$을 사용해야 합니다. 이것은 오직 $n$에 의존하고 그것의 밀도가 명시적으로 표현될 수 있는 분포의 형성을 허용합니다.

정의: 연속 확률 변수가, 만약 그것의 확률 밀도가 $-\infty <x<\infty$에 대해 $f(x)=\left(k_{m}\left(1+{\frac {x^{2}}{m}}\right)\right)^{\frac {-m+1}{2}}$로 주어지면, 매개-변수 m을 갖는 t-분포이며, 여기서 $m\geq 1$는 정수이고, $k_{m}={\frac {\Gamma \left({\frac {m+1}{2}}\right)}{{\sqrt {m\pi }}\,\Gamma \left({\frac {m}{2}}\right)}}$입니다. 이 분포는 $t(m)$으로 표시되고 m 자유도를 갖는 t-분포로 참조됩니다.

예제: t-분포(t-distribution) 테이블을 사용하여

1. 표본 크기로부터 자유도(degrees of freedom) (df)를 찾으십시오:

만약 표본 크기 = 10이면, df = 9입니다.

2. 1로부터 신뢰 구간을 빼고 그런-다음, 2로 그것을 나누십시오. 이 값은 $\alpha$ 수준입니다. ($\alpha$ + CL = 1)

3. t-분포 테이블에서 df와 $\alpha$를 찾으십시오. df = 9와 $\alpha$ = 0.01에 대해, 테이블은 2.281의 값을 제공합니다. 테이블에서 얻어진 이 값은 t-점수입니다.

Statistical theory

Definition

X를 통계적 매개-변수(statistical parameter) θ와 φ를 갖는 확률 분포(probability distribution)로부터 확률 표본(random sample)으로 놓으며, 여기서 θ는 추정되려는 양이고, φ는 즉각적인 관심이 없는 양을 나타냅니다. 신뢰 수준 또는 신뢰 계수 γ를 갖는, 매개-변수 θ에 대해 신뢰 구간은, 다음 속성을 갖는, 확률 변수(random variable)의 쌍 u(X) 및 v(X)에 의해 결정되는 확률 끝점 (u(X), v(X))을 갖는 구간입니다:

${\Pr }_{\theta ,\varphi }(u(X)<\theta <v(X))=\gamma {\text{ for all }}(\theta ,\varphi ).$

즉각적인 관심이 없는 양 φ는 장애 매개-변수(nuisance parameter)로 불리는데, 왜냐하면 통계적 이론이 여전히 그들을 처리할 어떤 방법을 찾아야 하기 때문입니다. 1에 가깝지만 1보다 크지 않은 전형적인 값을 갖는 숫자 γ는 때때로 형식 1 − α (또는 백분율 100%·(1 − α))으로 주어지며, 여기서 α는 0에 가까운 작은 비-음의 숫자입니다.

여기서 Pr_θ,φ은 (θ, φ)에 의해 특징지어지는 X의 확률 분포를 나타냅니다. 이 명세의 중요한 부분은 확률 구간 (u(X), v(X))이 실제 θ의 참 값이 무엇이든 상관없이 높은 확률을 갖는 미지수 값 θ를 덮는다는 것입니다.

여기서 Pr_θ,φ은, 비록 종종 그럴지라도, 명시적으로 주어진 매개변수화된 분포의 가족을 참조할 필요는 없음을 주목하십시오. 확률 변수 X가 같은 모집단으로부터 또는 실재의 같은 버전에서 x의 다른 가능한 실현에 개념적으로 해당하는 것처럼, 매개-변수 (θ, φ)는 우리가 X의 분포가 다른 형질을 가질 수 있는 실재의 다른 버전을 고려해야 한다는 것을 나타냅니다.

특정 상황에서, x가 표본 X의 결과일 때, 구간 (u(x), v(x))은 θ에 대해 신뢰 구간으로 역시 참조됩니다. 더 이상 (관찰된) 구간 (u(x), v(x))은 매개-변수 θ를 포함할 확률 γ를 가짐을 말할 수 없음에 주목하십시오. 이 관측된 구간은 확률 명제가 유지되는 모든 가능한 구간의 단지 하나의 실현입니다.

Approximate confidence intervals

많은 응용에서, 정확히 요구된 신뢰 수준을 갖는 신뢰 구간은 구성하기 어렵습니다. 그러나 실제로 유용한 구간은 여전히 구할 수 있습니다: 구간을 구성하는 규칙은 근사의 수락-가능한 수준에 대한 만약 다음이면 레벨 γ에서 신뢰 구간을 제공하는 것으로 수락될 수 있습니다:

${\Pr }_{\theta ,\varphi }(u(X)<\theta <v(X))\approx \gamma {\text{ for all }}(\theta ,\varphi )\,$

대안적으로, 일부 저자는 다음임을 단순히 요구합니다:

${\Pr }_{\theta ,\varphi }(u(X)<\theta <v(X))\geq \gamma {\text{ for all }}(\theta ,\varphi )\,$

이것은 만약 확률이 오직 부분적으로 식별 또는 부정확한(imprecise) 것이면, 및 역시 이산 분포(discrete distributions)를 다룰 때 유용합니다. 형식 ${\Pr }_{\theta ,\varphi }(u(X)<\theta )\geq \gamma$ and ${\Pr }_{\theta ,\varphi }(\theta <v(X))\geq \gamma$의 신뢰 극한은 보수적(conservative)이라고 불립니다; 그에 따라서, 우리는 보수적 신뢰 구간 및, 일반적으로, 영역에 대해 말합니다.

Desirable properties

표준 통계 절차를 적용할 때, 종종 신뢰 구간을 구성하는 표준 방법이 있을 것입니다. 이것들은 특정 바람직한 속성을 충족시키기 위해 고안되어 왔을 것이며, 이것은 절차가 의존하는 가정이 참임을 주어지며 유지될 것입니다. 이들 바람직한 속성은 유효성, 최적성, 및 불변성으로 설명될 수 있습니다. 이들 중 "유효성"이 가장 중요하며, 그 뒤에 "최적성"이 뒤따릅니다. "불변성"은 구간 구성하는 것에 대해 규칙이 아닌 신뢰 구간의 도출의 방법의 속성으로 여길 수 있습니다. 비-표준 응용에서, 같은 바람직한 속성이 요구될 것이다.

• 유효성(Validity). 이것은 신뢰 구간의 명목 적용-범위 확률(coverage probability) (신뢰 수준)이, 정확하게 또는 좋은 근사임을 유지되어야 함을 의미합니다.
• 최적성(Optimality). 이것은 신뢰 구간 구성에 대해 규칙이 데이터-집합에서 정보를 가능한 많이 사용해야 한다는 것을 의미합니다. 우리는 데이터-집합의 절반을 버릴 수 있고 여전히 유효한 신뢰 구간을 도출할 수 있음을 상기하십시오. 최적성을 평가하는 한 가지 방법은 신뢰 구간을 구성하는 것에 대해 규칙이 만약 길이가 전형적으로 더 짧은 구간으로 이어지면 다른 것보다 좋은 것으로 판단되도록 신뢰 구간의 길이에 의한 것입니다.
• 불변성(Invariance). 많은 응용에서, 추정되는 양은 그렇게 엄격하게 정의되지 않을 수 있습니다. 예를 들어, 조사는 모집단에서 평균 소득의 추정을 초래할 수 있지만, 이것이 그래픽 결과를 나타내는 것에 대해 공통 스케일인 것으로 주어지면, 중앙 소득의 로그의 추정을 제공하는 것으로 같게 여길 수 있을 것입니다. 중앙 소득에 대해 신뢰 구간을 구성하는 데 사용된 방법이 중앙 소득의 로그에 대해 신뢰 구간을 구성하는 것에 적용될 때 동등한 결과를 제공하는 것이 바람직할 것입니다: 구체적으로 특히 후자 구간의 끝에서 그 값은 전자 구간의 끝에서 값의 로그가 될 것입니다.

Methods of derivation

비-표준 응용에서, 신뢰 구간의 구성에 대해 규칙을 도출하기 위해 취할 수 있는 여러 경로가 있습니다. 표준 절차에 대해 확립된 규칙은 이들 여러 경로를 통해 정당화되거나 설명될 수 있습니다. 전형적으로 신뢰 구간을 구성하기 위한 규칙은 고려되는 양의 점 추정(point estimate)을 찾는 특정 방법과 밀접한 묶이게 됩니다.

요약 통계(Summary statistics)

이것은 추정에 대해 모멘트의 방법(method of moments)과 밀접한 관련됩니다. 단순한 예제는 추정되는 양이 평균인 곳에서 발생하며, 이 경우에서 자연스러운 추정은 표본 평균입니다. 일반적인 인수는 표본 분산이 표본 평균의 분산을 추정하기 위해 사용될 수 있음을 나타냅니다. 참 평균에 대해 신뢰 구간은 표본 분산의 제곱근의 배수인 폭을 갖는 표본 평균을 중심으로 구성될 수 있습니다.

가능도 정리(Likelihood theory)

추정이 최대 가능도 원리(maximum likelihood principle)를 사용하여 구성되는 곳에서, 이것에 대해 이론은 추정에 대해 신뢰 구간 또는 신뢰 범위를 구성하는 두 가지 방법을 제공합니다. 한 가지 방법은 윌크스의 이론(Wilks's theorem)을 사용함으로써 다음 제한을 충족시키는 $\theta$의 모든 가능한 값을 찾는 것입니다:

$\ln(L(\theta ))\geq \ln(L({\hat {\theta }}))-{\frac {1}{2}}\chi _{1,1-\alpha }^{2}$

추정하는 방정식(Estimating equations)

여기서 추정 접근법은 모멘트의 방법의 일반화와 최대 가능도 접근법의 일반화 둘 다로 여길 수 있습니다. 신뢰 구간을 추정하는 방정식(estimating equations)으로부터 도출된 추정에 기초하여 구성되는 것을 허용하는 최대 가능도 이론의 결과의 해당하는 일반화가 있습니다.

가설 테스팅(Hypothesis testing)

만약 중요성 테스트는 매개-변수의 일반적인 값에 대해 유효하면, 신뢰 구간/범위는 100p% 신뢰 범위에서 모든 그들의 점을 포함함으로써 구성될 수 있으며 이것에 대해 참값이 주어진 값이라는 무 가설의 중요성 테스트가 (1 − p)의 중요성 수준에서 거절되지 않습니다.

부트스래핑(Bootstrapping)

위의 방법에 대해 분포 가정이 불확실 또는 위반되는 상황에서, 다시-표본화하는 방법은 신뢰 구간 또는 예측 구간의 구성을 허용합니다. 관측된 데이터 분포와 내부 상관-관계는 더 넓은 모집단에서 상관-관계에 대해 대리로 사용됩니다.

Examples

Practical example

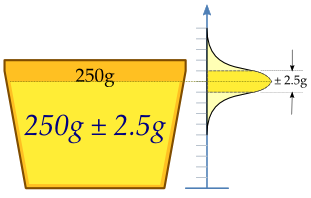
기계는 컵에 액체를 채우고, 컵의 내용물이 250g의 액체가 되도록 조정되어야 합니다. 기계는 모든 각 컵에 정확히 250.0g을 채울 수 없으므로, 개별 컵에 더해진 내용물은 약간의 변동을 뵈이고, 확률 변수 X로 여겨집니다. 이 변동은 2.5g의 표준 편차(standard deviation), σ를 갖는 250g의 원하는 평균 주위에 정규적으로 분포(normally distributed)되는 것으로 가정됩니다. 만약 기계가 적절하게 보정되었음을 결정하기 위해, 액체의 n = 25 컵의 표본이 무작위로 선택되고 컵의 무게가 측정됩니다. 결과적으로 측정된 액체의 질량은 X로부터 무작위 표본, X₁, ..., X₂₅입니다.

기대 μ의 자국을 얻기 위해, 추정을 제공하는 것으로 충분합니다. 적절한 추정기(estimator)는 표본 평균입니다:

${\hat {\mu }}={\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}.$

표본은 다음 평균과 함께 실제 무게 x₁, ..., x₂₅을 보여줍니다:

${\bar {x}}={\frac {1}{25}}\sum _{i=1}^{25}x_{i}=250.2{\text{ grams}}.$

만약 우리가 25 컵의 또 다른 표본을 취하면, 우리는 250.4 또는 251.1 그램과 같은 평균값을 쉽게 찾을 것으로 예상될 수 있습니다. 280 그램의 표본 평균값은 어쨌든 만약 컵의 평균 내용물은 사실 250 그램에 가까우면 극히 드물게 됩니다. 만약 전체 모집단 평균이 실제로 이 범위 안의 값을 취하면, 관측된 데이터가 특별히 별난 것으로 여겨지지 않는 것 이내의 표본 평균의 관측 값 250.2 그램 주위에 전체 구간이 있습니다. 그러한 구간은 매개-변수 μ에 대해 신뢰 구간이라고 불립니다. 우리가 그러한 구간을 어떻게 계산합니까? 구간의 끝점은 표본에서 계산되어야 하므로, 그들은 표본 X₁, ..., X₂₅의 통계량, 함수이고 따라서 확률 변수 자체입니다.

우리의 경우에서 우리는 정규적으로 분포된 표본으로부터 표본 평균 X가 역시 같은 기대 μ를 갖지만, 다음의 표준 오차(standard error)를 갖는 정규적으로 분포되는 것으로 고려함으로써 끝점을 결정할 수 있습니다:

${\frac {\sigma }{\sqrt {n}}}={\frac {2.5{\text{ g}}}{\sqrt {25}}}=0.5{\text{ grams}}$

표준화(standardizing)함으로써, 우리는 추정되려는 매개-변수 μ에 의존하지만, 매개-변수 μ와 독립적인 표준 정규 분포를 갖는 다음 확률 변수를 얻습니다:

$Z={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}={\frac {{\bar {X}}-\mu }{0.5}}$

따라서 μ와 독립적으로, 숫자 −z와 z를 찾을 수 있으며, 그 사이에서 Z는 확률 1 − α, 우리가 얼마나 신뢰하기를 원하는지의 측정으로 놓입니다.

우리는 예를 들어 1 − α = 0.95를 취합니다. 따라서 우리는 다음을 가집니다:

$P(-z\leq Z\leq z)=1-\alpha =0.95.$

숫자 z는 누적 분포 함수(cumulative distribution function)를 따르며, 이 경우에서 누적 정규 분포 함수(cumulative normal distribution function):

${\begin{aligned}\Phi (z)&=P(Z\leq z)=1-{\tfrac {\alpha }{2}}=0.975,\\[6pt]z&=\Phi ^{-1}(\Phi (z))=\Phi ^{-1}(0.975)=1.96,\end{aligned}}$

및 우리는 다음을 가집니다:

${\begin{aligned}0.95&=1-\alpha =P(-z\leq Z\leq z)=P\left(-1.96\leq {\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}\leq 1.96\right)\\[6pt]&=P\left({\bar {X}}-1.96{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\bar {X}}+1.96{\frac {\sigma }{\sqrt {n}}}\right).\end{aligned}}$

달리 말해서, 95% 신뢰 구간의 아래쪽 끝점은 다음입니다:

${\text{Lower endpoint}}={\bar {X}}-1.96{\frac {\sigma }{\sqrt {n}}},$

그리고 95% 신뢰 구간의 위쪽 끝점은 다음입니다:

${\text{Upper endpoint}}={\bar {X}}+1.96{\frac {\sigma }{\sqrt {n}}}.$

이 예제에서 값과 함께, 신뢰 구간은 다음입니다:

${\begin{aligned}0.95&=\Pr({\bar {X}}-1.96\times 0.5\leq \mu \leq {\bar {X}}+1.96\times 0.5)\\[6pt]&=\Pr({\bar {X}}-0.98\leq \mu \leq {\bar {X}}+0.98).\end{aligned}}$

모집단 σ의 표준 편차가 이 경우에서 알려져 있으므로, 표본 평균 ${\bar {X}}$의 분포는 유일한 미지수 매개-변수 $\mu$를 갖는 정규 분포(normal distribution)입니다. 아래의 이론적 예제에서 매개-변수 σ는 역시 미지수이며, 그것은 스튜던트의 t-분포(Student's t-distribution)를 사용하는 것을 요청합니다.

Interpretation

이것은 다음으로 해석될 수 있습니다: 확률 0.95와 함께 우리는 매개-변수 μ의 값이 확률론적 다음 두 끝점 사이에 있을 신뢰 구간을 찾을 것입니다:

$\!{\bar {X}}-0{.}98$

및

$\!{\bar {X}}+0.98.$

이것은 매개-변수 μ의 값이 표본 평균의 현재 계산된 값을 사용함으로써 얻어진 구간 안에 있을 확률이 0.95라는 의미는 아닙니다:

$({\bar {x}}-0.98,\,{\bar {x}}+0.98).$

대신에, 측정이 반복될 때마다, 표본의 평균 X에 대해 또 다른 값이 있을 것입니다. 그 경우의 95%에서 μ는 이 평균으로부터 계산된 끝점 사이에 있을 것이지만, 그 경우의 5%에서 그렇지 않을 것입니다. 실제 신뢰 구간은 공식에서 측정된 질량을 입력함으로써 계산됩니다. 우리의 0.95 신뢰 구간은 다음이 됩니다:

$({\bar {x}}-0.98;{\bar {x}}+0.98)=(250.2-0.98;250.2+0.98)=(249.22;251.18).\,$

The blue vertical line segments represent 50 realizations of a confidence interval for the population mean μ, represented as a red horizontal dashed line; note that some confidence intervals do not contain the population mean, as expected.

다시 말해, 95% 신뢰 구간은 아래쪽 끝점 249.22g과 위쪽 끝점 251.18g 사이에 있습니다.

원하는 μ의 값 250이 결과 신뢰 구간 이내에 있으므로, 기계가 잘못 보정되었다고 믿을 이유가 없습니다.

계산된 구간은 고정된 끝점을 가지며, 여기서 μ는 사이에 있을 수 (또는 없을 수) 있습니다. 따라서 이 사건은 확률 0 또는 1을 가집니다. 우리는 다음처럼 말해서는 안됩니다: "확률 (1 − α)와 함께 매개-변수 μ는 신뢰 구간 안에 놓입니다." 우리는 그 경우의 100(1 − α)%에서 반복에 의해, μ는 계산된 구간 안에 있을 것임을 오직 알고 있습니다. 그 경우의 100α%에서 어쨌든 그렇지 않습니다. 그리고 불행하게도 우리는 어떤 경우에 이것이 발생하는지 알 수 없습니다. 그것이 (용어 "확률"을 사용하는 대신에) 우리가 "신뢰 수준 100(1 − α) %과 함께, μ는 신뢰 구간 안에 놓일 것"이라고 말할 수 있는 이유입니다.

최대 오차는 0.98로 계산되는데 왜냐하면 그것이 우리가 위쪽 또는 아래쪽 끝점을 갖는 것을 확신하는 값 사이의 차이이기 때문입니다.

오른쪽 그림은 주어진 모집단 평균 μ에 대해 신뢰 구간의 50 실현을 보여줍니다. 만약 우리가 하나의 실현을 무작위로 선택하면 확률은 95%이며 우리는 매개-변수를 포함하는 구간을 선택하게 됩니다; 어쨌든, 우리는 운이 좋지 않고 잘못된 것을 선택할 수 있습니다. 우리는 결코 알지 못할 것입니다; 우리는 우리의 구간에 갇혀 있습니다.

Practical example extension: importance of confidence intervals in medical research

의료 연구는 종종 특정 모집단에서 중재 또는 노출의 영향을 추정합니다. 보통, 연구원은 p-값에 따라 효과의 중요성을 결정해 왔습니다; 어쨌든, 최근에는 추정에 대해 더 강력한 기반을 제공하기 위해 더 많은 통계 정보를 추진해 왔습니다. 이 문제를 해결하는 한 가지 방법은 신뢰 구간의 보고하는 것을 역시 요구하는 것입니다. 아래는 신뢰 구간이 연구에 사용 및 보고되는 방법에 대한 두 가지 예제입니다:

Example 1

2004 연구에서, 브리튼과 동료 연구자들은 난소암에 대한 불임의 관계를 평가하는 것에 대한 연구를 수행했습니다. 발생률 1.98은 1.4%에서 2.6까지의 비율을 갖는 95% 신뢰 (CI) 구간에 대해 보고되었습니다. 통계량은 이 논문에서 다음으로 보고되었습니다: "(표준화된 발생률 = 1.98; 95% CI, 1.4–2.6)." 이것은, 연구된 표본에 근거하여, 불임 여성은 난소암 발생률이 불임 여성보다 1.98배 더 높음을 의미합니다. 게다가, 우리는 모든 불임 여성 모집단에서 참 발생률이 1.4에서 2.6 범위에 놓인다고 95% 확신함을 역시 의미합니다. 그러므로, 참 발생률이 1.4에서 2.6 값의 범위 밖에 놓일 5% 확률이 있습니다. 전체적으로, 신뢰 구간은 연구된 변수에 대해 발생할 수 있는 가장-낮은 및 가장-높은 영향을 보고하면서 여전히 관찰된 영향의 중요성에 대한 정보를 제공한다는 통계적 정보를 더 많이 제공했습니다.

Example 2

2018년 연구에서, 미국 성인 모집단에서 아토피성 피부염의 유병률과 질병 부담은 95% 신뢰 구간의 사용과 함께 이해되었습니다. 참여 성인 1,278명 중에서, 아토피성 피부염의 유병률은 7.3% (5.9–8.8)임을 보고되었습니다. 게다가, 참가자의 60.1% (56.1–64.1)는 가벼운 아토피성 피부염으로 분류된 반면에 28.9% (25.3–32.7)는 보통이었고 11% (8.6–13.7)는 심했습니다. 그 연구는 모집단에서 아토피성 피부염의 높은 유병률과 질병 부담이 있음을 확인했습니다.

Theoretical example

{X₁, ..., X_n}이 미지수 (매개-변수(parameters)) 평균(mean) μ 및 분산(variance) σ²을 갖는 정규적으로 분포된(normally distributed) 모집단으로부터 독립(independent) 표본이라고 가정합니다. 다음을 놓습니다:

${\bar {X}}=(X_{1}+\cdots +X_{n})/n\,,$

$S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\bar {X}}\,)^{2}.$

여기서 X는 표본 평균(sample mean)이고, S²은 표본 분산(sample variance)입니다. 그런-다음

$T={\frac {{\bar {X}}-\mu }{S/{\sqrt {n}}}}$

은 n − 1 자유도를 갖는 스튜던트의 t-분포(Student's t-distribution)를 가집니다. T의 분포는 비-관찰가능한 매개-변수 μ 및 σ²의 값에 의존하지 않음에 주목하십시오; 즉, 그것은 중추적 양(pivotal quantity)입니다. 우리는 μ에 대해 95% 신뢰 구간을 계산하려고 원했던 것으로 가정합니다. 그런-다음, c를 이 분포의 97.5번째 백분위수(percentile)로 나타냅니다.

$\Pr(-c\leq T\leq c)=0.95\,$

"97.5번째"와 "0.95"는 앞의 표현에서 정확한 것임에 주목하십시오. $T$가 $-c$보다 적을 2.5% 기회가 있고, 그것이 $+c$보다 클 2.5% 기회가 있습니다. 따라서, $T$가 $-c$와 $+c$ 사이에 있을 확률은 95%입니다.

결론적으로,

$\Pr \left({\bar {X}}-{\frac {cS}{\sqrt {n}}}\leq \mu \leq {\bar {X}}+{\frac {cS}{\sqrt {n}}}\right)=0.95\,$

이고 우리는 μ에 대해 이론적으로 (통계적으로) 95% 신뢰 구간을 가집니다.

표본을 관찰한 후에 우리는 X에 대해 값 x를 찾고 S에 대해 값 s를 찾으며, 그것으로부터 우리는 다음 신뢰 구간을 계산합니다:

$\left[{\bar {x}}-{\frac {cs}{\sqrt {n}}},{\bar {x}}+{\frac {cs}{\sqrt {n}}}\right],\,$

끝점으로 고정된 숫자를 갖는 구간이며, 우리는 그것이 매개-변수 μ를 포함하는 특정 확률이 있음을 더 이상 말할 수 없습니다; μ는 이 구간 안에 있던지 그렇지 않던지 중의 하나입니다.

Alternatives and critiques

Main article: Interval estimation

신뢰 구간은 구간 추정(interval estimation)의 한 방법이고 빈도주의 통계(frequentist statistics)에서 가장 널리 사용됩니다. 베이즈 통계(Bayesian statistics)에서 유사한 개념은 신용 구간(credible interval)이지만, 대안적인 빈도주의 방법은 매개-변수를 추정하는 대신에 미래 표본의 결과를 추정하는 예측 구간(prediction interval)의 방법입니다. 구간을 사용하여 불확실성을 표현하는 것에 대한 다른 접근에 대해, 구간 추정(interval estimation)을 참조하십시오.

Comparison to prediction intervals

Main article: Prediction interval

확률 변수(random variable)에 대해 예측 구간(prediction interval)은 통계적 매개-변수(statistical parameter)에 대해 신뢰 구간과 유사하게 정의됩니다. 확률 변수(random variable) X에 통계적으로 의존적이거나 의존하지 않을 수 있는 추가적인 확률 변수(random variable) Y를 생각해 보십시오. 그런-다음 (u(X), v(X))는 Y의 만약 다음이면 아직까지 관측된 값 y에 대해 예측 구간(prediction interval)을 제공합니다:

${\Pr }_{\theta ,\varphi }(u(X)<Y<v(X))=\gamma {\text{ for all }}(\theta ,\varphi ).\,$

여기서 Pr_θ,φ은 확률 변수 (X, Y)의 결합 확률 분포(joint probability distribution)를 나타내며, 여기서 이 분포는 통계적 매개-변수(statistical parameter) (θ, φ)에 의존합니다.

Comparison to tolerance intervals

Main article: Tolerance interval

Comparison to Bayesian interval estimates

See also: Credible interval § Confidence interval

베이즈 구간 추정은 신용 구간(credible interval)으로 불립니다. 위와 같은 표기법을 많이 사용하여, 미지수 참 값 θ에 대해 신용 구간의 정의는, 주어진 γ에 대해, 다음입니다:

$\Pr(u(x)<\Theta <v(x)\mid X=x)=\gamma .\,$

여기서 Θ는 미지수 θ의 값은 확률 변수로 취급되고 있음을 강조하기 위해 사용됩니다. 구간의 두 가지 유형의 정의는 다음처럼 비교될 수 있습니다.

• 신뢰 구간의 정의는 주어진 (θ, φ) (또는 이들 값에 대한 조건부)에 대해 X의 분포로부터 계산된 확률을 포함하고 조건은 (θ, φ)의 모든 값에 대해 유지되어야 합니다.
• 신용 구간의 정의는 X = x의 관측된 및 Φ의 값에 걸쳐 주변화된 (또는 평균된) 값에 대한 조건부 θ의 분포에서 계산된 확률을 포함하며, 여기서 이 마지막 양은 φ에서 장애 매개-변수(nuisance parameter)에 대한 불확실성에 해당하는 확률 변수입니다.

위의 장애 매개-변수의 처리는 신뢰와 신용 구간을 비교하는 토론에서 종종 생략되지만 그것은 두 경우 사이에 현저하게 다름을 주목하십시오.

일부 간단한 표준 경우에서, 같은 데이터 집합에서 신뢰와 신용 구간으로 생성된 구간이 동일할 수 있습니다. 그들은 만약 유익한 이전 정보(prior information)가 베이즈 해석(Bayesian analysis)에 포함되면 매우 다를 수 있고, 심지어 만약 베이즈 이전이 상대적으로 무-정보적(uninformative)일지라도, 가능한 데이터의 공간의 어떤 부분에 대해 매우 다를 수 있습니다.

이들 방법의 어떤 것이 가장 유용한 결과를 생성하는지에 대한 일치된 의견이 없습니다: 계산의 수학은 문제에서 –표본화 분포를 기반으로 하는 신뢰 구간, 베이즈의 정리(Bayes' theorem)를 기반으로하는 신용 구간– 드물지만, 이들 방법의 적용, 생산된 통계량의 유용성 및 해석은 논란이 있습니다.

Confidence intervals for proportions and related quantities

See also: Margin of error and Binomial proportion confidence interval

모집단에 대해 근사 신뢰 구간은, 만약 표본 크기(sample size)와 계산이 충분히 크면, 중심 극한 정리(central limit theorem)에 의존하는, 모집단에서 정규적으로 분포되지 않은 확률 변수에 대해 구성될 수 있습니다. 그 공식은 위의 경우와 동일합니다 (여기서 표본 평균이 모집단 평균에 대한 실제로 정규적으로 분포됩니다). 근사는 만약 확률 변수의 확률 분포(probability distribution)가 정규 분포(normal distribution)와 너무 다르면 (예를 들어, 누적 분포 함수(cumulative distribution function)가 임의의 불연속성(discontinuities)을 가지지 않고 기울어짐(skewness)이 보통입니다) 표본에서 오직 수십 개의 관측을 갖는 꽤 좋은 근사일 것입니다.

표본 평균의 한 유형은 지시기 변수(indicator variable)의 평균이며, 이것이 참에 대해 값 1 및 거짓에 대해 값 0을 취합니다. 그러한 변수의 평균은 (모집단 및 임의의 표본 둘 다에서) 1과 같은 변수를 가지는 비율과 같습니다. 이것은 지시기 변수, 특히 가설 테스팅에 대해 특히 유용한 속성입니다. 중심 극한 정리를 적용하기 위해, 우리는 충분하게 큰 표본을 사용해야 합니다. 대략적인 엄지의 규칙은 우리가 지표가 1인 것에서 적어도 5 경우, 그것이 0인 것에서 적어도 5 경우이어야 한다는 것입니다. 위의 공식을 사용하여 구성된 신뢰 구간은 음수 또는 1보다 큰 숫자를 포함할 수 있지만, 비율은 분명히 음수 또는 1을 초과할 수 없습니다. 추가적으로, 표본 비율은 값의 한정된 숫자를 오직 취할 수 있으므로, 중심 극한 정리와 정규 분포는 신뢰 구간을 구축하기 위한 최상의 도구가 아닙니다. 이 경우에 더 적합한 방법에 대해 "이항 비율 신뢰 구간(Binomial proportion confidence interval)"을 참조하십시오.

Counter-examples

신뢰 구간 이론이 제안되었으므로, 그 이론에 대한 많은 반대-예제가 신뢰 구간의 해석이 문제가 얼마나 문제가 될 수 있는지, 적어도 만약 우리가 그것을 순진하게 해석한다면, 보여주기 위해 개발되어 왔습니다.

Confidence procedure for uniform location

웰치는 신뢰 구간의 이론과 구간 추정의 다른 이론 (피셔의 기준(fiducial) 구간과 객관적인 베이즈(Bayesian) 구간을 포함) 사이의 차이를 명확하게 보여주는 예제를 제시했습니다. 로빈슨은 이 예제를 "[신]뢰 구간 이론의 네이만의 버전에 대해 가장 잘 알려진 반례"라고 불렀습니다. 웰치에게, 그것은 신뢰 구간 이론의 우월성을 보였습니다; 그 이론의 비평가들에게, 그것은 부족으로 보입니다. 여기서 우리는 단순화된 버전을 제공합니다.

$X_{1},X_{2}$가 균등(Uniform)(θ − 1/2, θ + 1/2) 분포에서 독립 관측으로 가정합니다. 그런-다음 최적의 50% 신뢰 절차는 다음입니다:

${\bar {X}}\pm {\begin{cases}{\dfrac {|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|<1/2\\[8pt]{\dfrac {1-|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|\geq 1/2.\end{cases}}$

기준 또는 객관적인 베이즈 인수는 구간 추정을 도출하기 위해 사용될 수 있습니다:

${\bar {X}}\pm {\frac {1-|X_{1}-X_{2}|}{4}},$

이것은 역시 50% 신뢰 절차입니다. 웰치는, 신뢰 구간 이론으로부터 데시데라타에 따르면, 첫 번째 신뢰 절차가 두 번째를 지배한다는 것을 보였습니다; 모든 각 $\theta _{1}\neq \theta$에 대해, 첫 번째 절차가 $\theta _{1}$을 포함할 확률은 두 번째 절차가 $\theta _{1}$을 포함할 확률보다 작거나 같습니다. 첫 번째 절차로부터 구간의 평균 너비는 두 번째의 그것보다 작습니다. 따라서, 첫 번째 절차는 고전적 신뢰 구간 이론 아래에서 선호됩니다.

어쨌든, $|X_{1}-X_{2}|\geq 1/2$일 때, 첫 번째 절차로부터 구간은 참값 $\theta$을 포함하는 것으로 보장됩니다: 그러므로, 명목상의 50% 신뢰 계수는 불확실성과 관련되지 않으며 우리는 특정 구간이 참값을 포함함을 가져야 합니다. 두 번째 절차는 이 속성을 가지지 않습니다.

게다가, 첫 번째 절차가 매우 짧은 구간을 생성할 때, 이것은 $X_{1},X_{2}$가 함께 매우 근접하고 따라서 단일 데이터 점에서 정보를 오직 제공함을 나타냅니다. 그래도 첫 번째 구간은 그것의 짧은 너비에 기인하여 매개-변수의 거의 모든 합리적인 값을 제외할 것입니다. 두 번째 절차는 이 속성을 가지지 않습니다.

첫 번째 절차의 두 가지 반대-직관적 속성—$X_{1},X_{2}$가 멀리 떨어져 있을 때 100% 적용범위이고 $X_{1},X_{2}$가 함께 가까울 때 거의 0% 적용범위—은 평균에 대한 50% 적용범위를 산출하기 위해 균형을 유지합니다. 어쨌든, 첫 번째 절차는 최적임에도 불구하고, 그것의 구간은 추정의 정밀도의 평가를 나타내지 못하거나 불확실성의 평가를 나타내지 못하며 우리는 구간이 참값을 포함함을 가져야 합니다.

이 반대-예제는 신뢰 구간의 순진한 해석에 반대하는 데 사용됩니다. 만약 신뢰 절차가 명목상의 적용범위의 (정밀도에 대한 관계, 또는 베이즈 추론과의 관계와 같은) 그것을 넘어서 속성을 갖는 것으로 주장되면, 그들의 속성은 입증되어야 합니다; 그들은 절차가 신뢰 절차라는 사실을 따르지 않습니다.

Confidence procedure for ω²

스타이거는 ANOVA에서 공통 효과 크기(effect size) 측정에 대해 여러 가지 신뢰 절차를 제안했습니다. Morey et al.은, ω²에 대해 하나를 포함하여, 이들 신뢰 절차의 여럿은 F 통계량이 점점 작아짐에 따라—ω²의 가능한 모든 값에 맞지 않음을 나타냄—신뢰 구간이 줄어들고 심지어 오직 단일 값 ω² = 0을 포함할 수 있다는 속성을 가집니다; 즉, CI는 무한소적으로 좁습니다 (이것은 $100(1-\alpha )\%$ CI에 대해 $p\geq 1-\alpha /2$일 때 발생합니다).

이 동작은 신뢰 절차와 유의성 테스팅 사이의 관계와 일치합니다: F가 너무 작아 그룹 평균이 우연히 예상한 것보다 훨씬 더 가깝기 때문에, 중요성 테스트는 ω²의 대부분 또는 모든 값에 대해 거절을 나타낼 수 있습니다. 따라서 구간이 매우 좁거나 심지어 비어 있습니다 (또는, 스타이거에 의해 제안된 관례에 의해, 오직 0을 포함합니다). 어쨌든, 이것은 ω²의 추정이 매우 정확하다는 것을 나타내지 않습니다. 하나의 의미에서, 결과 자체의 신뢰성이 의문의 여지가 있는 것이 반대를 나타냅니다. 이것은 추정의 정확성을 드러내는 신뢰 구간의 공통적인 해석과 상반됩니다.

See also

• Cumulative distribution function-based nonparametric confidence interval
• CLs upper limits (particle physics)
• Confidence distribution
• Credence (statistics)
• Error bar
• Estimation statistics
• p-value
• Robust confidence intervals
• Confidence region
• Credible interval

Confidence interval for specific distributions

• Confidence interval for binomial distribution
• Confidence interval for exponent of the power law distribution
• Confidence interval for mean of the exponential distribution
• Confidence interval for mean of the Poisson distribution
• Confidence intervals for mean and variance of the normal distribution

Bibliography

• Mehta, S. (2014) Statistics Topics ISBN 978-1-4992-7353-3
• "Confidence estimation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. (2016). "The fallacy of placing confidence in confidence intervals". Psychonomic Bulletin & Review. 23 (1): 103–123. doi:10.3758/s13423-015-0947-8. PMC 4742505. PMID 26450628.

External links

• The Exploratory Software for Confidence Intervals tutorial programs that run under Excel
• Confidence interval calculators for R-Squares, Regression Coefficients, and Regression Intercepts
• Weisstein, Eric W. "Confidence Interval". MathWorld.
• CAUSEweb.org Many resources for teaching statistics including Confidence Intervals.
• An interactive introduction to Confidence Intervals
• Confidence Intervals: Confidence Level, Sample Size, and Margin of Error by Eric Schulz, the Wolfram Demonstrations Project.
• Confidence Intervals in Public Health. Straightforward description with examples and what to do about small sample sizes or rates near 0.

Online calculators

• GraphPad QuickCalcs
• TAMU's Confidence Interval Calculators
• MBAStats confidence interval and hypothesis test calculators
• Stats Journal – statistics calculator online