Sample (statistics)

통계학(statistics) 및 양적 연구(quantitative research) 방법론에서, 표본(sample)은 정의된 절차에 의해 통계적 모집단(statistical population)으로부터 수집된 또는 선택된 개체 또는 대상의 집합입니다.^[1] 표본의 원소는 표본 점(sample points), 표본화 단위(sampling units) 또는 관측으로 알려져 있습니다^{[citation needed]}.

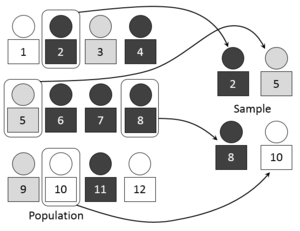
전형적으로, 모집단은 매우 크며, 조사(census)를 하거나 또는 모집단의 모든 값의 완전한 열거(enumeration)는 비실용적이거나 불가능합니다. 표본은 관리-가능한 크기의 부분-집합을 보통 나타냅니다. 표본은 수집되고 통계량(statistic)은, 우리가 표본으로부터 모집단으로의 추론(inference) 또는 외삽법(extrapolation)을 만들 수 있도록, 표본으로부터 계산됩니다.

표본은 복원없이(without replacement) 모집단으로부터 추출될 수 있으며 (즉, 원소는 같은 표본에서 한 번보다 많이 선택될 수 없습니다), 이 경우에서 표본은 모집단(population)의 부분-집합(subset)입니다; 또는 복원과 함께(with replacement)(즉, 원소가 한 표본에 여러 번 나타날 수 있습니다), 이런 경우에 표본은 중복-부분-집합입니다.^[2]

Kinds of samples

완전한 표본은 잘-정의된 선택 기준의 집합을 만족시키는 모든 그러한 대상을 포함하는 부모 모집단으로부터 대상의 집합입니다.^[3]^{[not in citation given]} 예를 들어, 2m보다 큰 호주 남성의 완전한 표본은 2m보다 큰 모든 각 호주 남성의 목록으로 구성됩니다. 그러나 그것은 독일 남성, 또는 키 큰 호주 여성, 또는 2m 미만의 사람들은 포함되지 않습니다. 따라서 그러한 완전한 표본을 수집하기 위해 해당 부모 모집단의 각 구성원에 대한 키, 성별, 및 국적에 대한 데이터를 포함하여 부모 모집단의 완전한 목록을 요구합니다. 사람 모집단의 경우에서, 그러한 완전한 목록이 존재하지 않을 것입니다 (사람 모집단은 수십억 명입니다). 그러나 그러한 완전한 표본은 종종 주요 스포츠 리그의 선수의 집합, 국회의원 생년월일, 또는 천체의 완전한 크기-제한된 목록과 같은 다른 분야에서 사용 가능합니다.

불-편향된 (대표적인) 표본은 대상의 속성에 의존하지 않는 선택 과정을 사용하여 완전한 표본에서 선택된 대상의 집합입니다.^[4] 예를 들어, 2m보다 큰 호주 남성의 불-편향 표본은 2m보다 큰 호주 남성의 1%의 무작위로 표본화된 부분-집합으로 구성될 수 있습니다. 그러나 선거 등록부에서 선택한 사람은 불-편향일 수 없는데 왜냐하면, 예를 들어, 18세 미만의 남성은 선거 등록부에 있지 않기 때문입니다. 천문학적 맥락에서, 불-편향 표본은 데이터가 이용-가능한 것에 대해 완전한 표본의 해당 부분을 구성할 수 있으며, 데이터 가용성이 개별 원천 속성에 의해 편향되지 않는 조건으로 제공됩니다.

편향 또는 비-대표하는 표본을 피하는 가장 좋은 방법은 확률 표본으로 역시 알려진 무작위 샘플(random sample)을 선택하는 것입니다. 무작위 표본은 모집단의 각 개별 구성원이 표본의 일부로 선택될 알려진, 비-영 기회를 가지는 표본으로 정의됩니다.^[5] 무작위 표본의 여러 유형은 단순 무작위 표본(simple random sample), 체계적 표본(systematic samples), 계층화된 확률 표본(stratified random samples), 및 클러스터 확률 표본(cluster random samples)입니다.

무작위가 아닌 표본은 비-무작위 표본(non-random sample) 또는 비-확률 표본화(non-probability sampling)라고 불립니다.^[6] 비-무작위 표본의 일부 예제는 편의 표본(convenience sample), 판단 표본(judgment sample), 의도가-있는 표본(purposive sample), 몫 표본(quota sample), 눈뭉치 표본(snowball samples), 및 준-몬테카를로 방법(quasi-Monte Carlo method)에서 구적법 노드(quadrature node)가 있습니다.

Mathematical description of random sample

수학적 조건에서, 확률 분포(probability distribution) F가 주어지면, 길이 n의 확률 표본 (여기서 n은 임의의 양의 정수일 수 있음)은 분포 F를 갖는 n 독립(independent), 동일하게 분포된 (iid) 확률 변수의 실현의 집합입니다.^[7]

표본은 구체적으로 같이 양이 측정되는 n 실험의 결과를 나타냅니다. 예를 들어, 만약 우리가 특정 모집단의 구성원의 평균 키를 추정하기를 원하면, 우리는 n 개인의 키를 측정합니다. 각 측정은 모집단을 특성화하는 확률 분포 F에서 가져 오므로, 각 측정된 높이 $x_{i}$ 는 분포 F를 갖는 임의 변수 $X_{i}$ 를 실현입니다. 확률 변수의 집합 (즉, 측정-가능한 함수의 집합)은 이들 변수 (이들 확률 변수가 취하는 값)의 실현과 혼동해서는 안됩니다. 달리 말해서, $X_{i}$ 는 i-번째 실험에서 측정을 나타내는 함수이고 $x_{i}=X_{i}(\omega )$ 는 측정을 만들 때 얻은 값입니다.

Notes

^ Peck, Roxy; Olsen, Chris; Devore, Jay (2008), Introduction to Statistics and Data Analysis (3rd ed.), Belmont, Cal.: Thomson Brooks/Cole, p. 8, ISBN 978-0-495-11873-2, LCCN 2006933904, retrieved 2009-08-04. {{cite book}}: Unknown parameter |last-author-amp= ignored (|name-list-style= suggested) (help)CS1 maint: url-status (link)
^ Borzyszkowski, Andrzej M.; Sokołowski, Stefan, eds. (1993), "A characterization of Sturmian morphisms" (PDF), Mathematical Foundations of Computer Science 1993. 18th International Symposium, MFCS'93 Gdańsk, Poland, August 30–September 3, 1993 Proceedings, Lecture Notes in Computer Science, vol. 711, pp. 281–290, CiteSeerX 10.1.1.361.7021, doi:10.1007/3-540-57182-5_20, ISBN 978-3-540-57182-7, Zbl 0925.11026
^ Pratt, J. W., Raiffa, H., and Schaifer, R. (1995). Introduction to Statistical Decision Theory. Cambridge, Mass.: MIT Press. ISBN 9780262161442. MR1326829
^ Lomax, R. G. and Hahs-Vaughan, Debbie L. An introduction to statistical concepts (3rd ed).
^ Cochran, William G. (1977). Sampling techniques (Third ed.). Wiley. ISBN 978-0-471-16240-7.
^ Johan Strydom (2005). Introduction to Marketing (Third ed.). Wiley. ISBN 978-0-471-16240-7.
^ Samuel S. Wilks, Mathematical Statistics, John Wiley, 1962, Section 8.1

External links

Statistical Terms Made Simple

[1] Peck, Roxy; Olsen, Chris; Devore, Jay (2008), Introduction to Statistics and Data Analysis (3rd ed.), Belmont, Cal.: Thomson Brooks/Cole, p. 8, ISBN 978-0-495-11873-2, LCCN 2006933904, retrieved 2009-08-04. {{cite book}}: Unknown parameter |last-author-amp= ignored (|name-list-style= suggested) (help)CS1 maint: url-status (link)

[BS1993-2] Borzyszkowski, Andrzej M.; Sokołowski, Stefan, eds. (1993), "A characterization of Sturmian morphisms" (PDF), Mathematical Foundations of Computer Science 1993. 18th International Symposium, MFCS'93 Gdańsk, Poland, August 30–September 3, 1993 Proceedings, Lecture Notes in Computer Science, vol. 711, pp. 281–290, CiteSeerX 10.1.1.361.7021, doi:10.1007/3-540-57182-5_20, ISBN 978-3-540-57182-7, Zbl 0925.11026

[3] Pratt, J. W., Raiffa, H., and Schaifer, R. (1995). Introduction to Statistical Decision Theory. Cambridge, Mass.: MIT Press. ISBN 9780262161442. MR1326829

[4] Lomax, R. G. and Hahs-Vaughan, Debbie L. An introduction to statistical concepts (3rd ed).

[5] Cochran, William G. (1977). Sampling techniques (Third ed.). Wiley. ISBN 978-0-471-16240-7.

[6] Johan Strydom (2005). Introduction to Marketing (Third ed.). Wiley. ISBN 978-0-471-16240-7.

[7] Samuel S. Wilks, Mathematical Statistics, John Wiley, 1962, Section 8.1

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Kinds of samples

Mathematical description of random sample

See also

Notes

External links