Cumulative distribution function

Original article: w:Cumulative distribution function

Cumulative distribution function for the exponential distribution

Cumulative distribution function for the normal distribution

확률 이론과 통계학에서, 실수-값 확률 변수(random variable) $X$는 누적 분포 함수(cumulative distribution function, 줄여서 CDF), 또는 $x$에서 평가되는 $X$의 단지 분포 함수(distribution function)는 가 $x$와 같거나 작은 값을 취할 확률입니다.

실수, 이산 또는 "혼합"과 마찬가지로 연속에서 지원되는 모든 각 확률 분포는 $\lim _{x\rightarrow -\infty }F(x)=0$와 $\lim _{x\rightarrow \infty }F(x)=1$를 만족시키는 오른쪽-연속 단조 증가하는 함수 (càdlàg 함수) $F:\mathbb {R} \rightarrow [0,1]$에 의해 고유하게 식별됩니다.

스칼라 연속 분포(continuous distribution)의 경우에서, 그것은 음의 무한대에서 $x$까지의 확률 밀도 함수(probability density function) 아래의 넓이를 제공합니다. 누적 분포 함수는 역시 다변수 확률 변수(multivariate random variables)의 분포를 지정하기 위해 사용됩니다.

Definition

실수-값 확률 변수(random variable) $X$의 누적 분포 함수는 다음에 의해 주어진 함수입니다:

$$F_{X}(x)=\operatorname {P} (X\leq x)$$

(Eq.1)

여기서 오른쪽 변은 확률 변수 $X$가 $x$보다 작거나 같은 값을 가질 확률(probability)을 나타냅니다.

$X$가 반-닫힌 구간 $(a,b]$에 있을 확률은, 여기서 $a<b$, 따라서 다음과 같습니다:

$$\operatorname {P} (a<X\leq b)=F_{X}(b)-F_{X}(a)$$

(Eq.2)

위의 정의에서, "작거나 같음" 기호, "≤"는 보편적으로 사용되는 기호가 아니라 관례이지만 (예를 들어, 헝가리 문헌에서는 "<"를 사용함), 그 구별은 이산 분포에서 중요합니다. 이항 분포(binomial)와 푸아송 분포(Poisson distributions)의 테이블의 적절한 사용은 이 관례에 따라 달라집니다. 게다가, 특성 함수(characteristic function)에 대해 폴 레비(Paul Lévy)의 역화 공식과 같은 중요한 공식도 "작거나 같음" 공식에 의존합니다.

만약 확률 변수 $X,Y,\ldots$ 등 여러 개를 다루면 해당 문자를 아래첨자로 사용하고, 반면에 오직 하나를 다루면, 아래첨자는 보통 생략됩니다. 확률 밀도 함수(probability density functions)와 확률 질량 함수(probability mass functions)에 사용되는 소문자 $f$와 달리 누적 분포 함수에 대문자 $F$를 사용하는 것이 편리합니다. 이것은 일반 분포를 논의할 때 적용됩니다: 일부 특정 분포는 고유한 전통적인 표기법을 가지며, 예를 들어, 정규 분포(normal distribution)는 각각 $F$와 $f$ 대신 $\Phi$와 $\phi$를 사용합니다.

연속 확률 변수의 확률 밀도 함수는 미적분의 기본 정리(Fundamental Theorem of Calculus)를 사용하여 미분함으로써 누적 분포 함수에서 결정될 수 있습니다; 즉, $F(x)$가 주어지면,$$f(x)={\frac {dF(x)}{dx}}$$ 도함수가 존재하는 한 만족합니다.

연속 확률 변수(continuous random variable) $X$의 CDF는 다음과 같이 확률 밀도 함수 $f_{X}$의 적분으로 표현될 수 있습니다: $$F_{X}(x)=\int _{-\infty }^{x}f_{X}(t)\,dt.$$

값 $b$에서 이산 성분을 가지는 분포를 가지는 확률 변수 $X$의 경우에서, $$\operatorname {P} (X=b)=F_{X}(b)-\lim _{x\to b^{-}}F_{X}(x).$$

만약 $F_{X}$가 $b$에서 연속이면, 이것은 영과 같고 $b$에 이산 성분이 없습니다.

Properties

From top to bottom, the cumulative distribution function of a discrete probability distribution, continuous probability distribution, and a distribution which has both a continuous part and a discrete part.

Example of a cumulative distribution function with a countably infinite set of discontinuities.

모든 각 누적 분포 함수 $F_{X}$는 비-감소하는 것이고 오른쪽-연속이며, 이는 càdlàg 함수가 됩니다. 게다가, $$\lim _{x\to -\infty }F_{X}(x)=0,\quad \lim _{x\to +\infty }F_{X}(x)=1.$$

이들 네 가지 속성을 갖는 모든 각 함수는 CDF입니다. 즉, 모든 각 그러한 함수에 대해, 확률 변수(random variable)는 함수가 해당 확률 변수의 누적 분포 함수임을 만족하도록 정의될 수 있습니다.

만약 $X$가 순전히 이산 확률 변수(discrete random variable)이면, 그것은 확률 $p_{i}=p(x_{i})$를 갖는 값 $x_{1},x_{2},\ldots$를 얻고, $X$의 CDF는 점 $x_{i}$에서 불연속(discontinuous)적입니다:$$F_{X}(x)=\operatorname {P} (X\leq x)=\sum _{x_{i}\leq x}\operatorname {P} (X=x_{i})=\sum _{x_{i}\leq x}p(x_{i}).$$

만약 실수 값 확률 변수 $X$의 CDF $F_{X}$가 연속(continuous)이면, $X$는 연속 확률 변수(continuous random variable)입니다; 더 나아가서 $F_{X}$가 절대적으로 연속(absolutely continuous)이라면, 모든 실수 $a$와 $b$에 대해 다음임을 만족하는 르베그-적분가능(Lebesgue-integrable) 함수 $f_{X}(x)$가 존재합니다: $$F_{X}(b)-F_{X}(a)=\operatorname {P} (a<X\leq b)=\int _{a}^{b}f_{X}(x)\,dx$$ 함수 $f_{X}$는 거의 모든 곳(almost everywhere)에서 $F_{X}$의 도함수와 같고, 그것은 $X$의 분포의 확률 밀도 함수(probability density function)라고 불립니다.

만약 $X$가 유한한 L1-노름(L1-norm), 즉, $|X|$의 기대는 유한하면, 기대는 리만–스틸티어스 적분(Riemann–Stieltjes integral)에 의해 제공됩니다:$$\mathbb {E} [X]=\int _{-\infty }^{\infty }tdF_{X}(t)$$그리고 임의의 $x\geq 0$에 대해, 다이어그램에 표시된 것처럼, 다음과 같습니다:

CDF plot with two red rectangles, illustrating $x(1-F_{X}(x))\leq \int _{x}^{\infty }tdF_{X}(t)$ and $xF_{X}(-x)\leq \int _{-\infty }^{-x}(-t)dF_{X}(t)$.

$${\begin{aligned}x(1-F_{X}(x))&\leq \int _{x}^{\infty }tdF_{X}(t)\\xF_{X}(-x)&\leq \int _{-\infty }^{-x}(-t)dF_{X}(t)\end{aligned}}$$특히, 다음을 가집니다: $$\lim _{x\to -\infty }xF(x)=0,\quad \lim _{x\to +\infty }x(1-F(x))=0.$$

Examples

하나의 예제로서, $X$가 단위 구간 $[0,1]$ 위에 균등하게 분포된다(uniformly distributed)고 가정합니다.

그런-다음 $X$의 CDF는 다음에 의해 지정됩니다:$$F_{X}(x)={\begin{cases}0&:\ x<0\\x&:\ 0\leq x\leq 1\\1&:\ x>1\end{cases}}$$

대신 $X$가 같은 확률을 갖는 이산 값 0과 1만 취한다고 가정합니다.

그런-다음 $X$의 CDF는 다음에 의해 지정됩니다: $$F_{X}(x)={\begin{cases}0&:\ x<0\\1/2&:\ 0\leq x<1\\1&:\ x\geq 1\end{cases}}$$

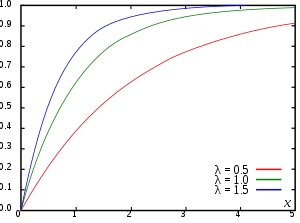
$X$가 지수 분포된(exponential distributed) 것이라고 가정합니다. 그런-다음 $X$의 CDF는 다음에 의해 지정됩니다: $$F_{X}(x;\lambda )={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$$

여기서 λ > 0는 종종 율 매개변수라고 불리는 분포의 매개변수입니다.

$X$는 정규 분포(normal distributed)라고 가정합니다. 그런-다음 $X$의 CDF는 다음에 의해 제공됩니다: $$F(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}\exp \left(-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\right)\,dt.$$

여기서 매개변수 $\mu$는 분포의 평균 또는 기대입니다; 그리고 $\sigma$는 표준 편차입니다.

표준 정규 분포의 CDF의 테이블은 종종 통계적 응용 프로그램에서 사용되며, 여기서 그것은 표준 정규 테이블(standard normal table), 단위 정규 테이블(unit normal table), 또는 Z 테이블(Z table)로 이름-짓습니다.

$X$가 이항 분포된(binomial distributed) 것이라고 가정합니다. 그런-다음 $X$의 CDF는 다음에 의해 제공합니다:$$F(k;n,p)=\Pr(X\leq k)=\sum _{i=0}^{\lfloor k\rfloor }{n \choose i}p^{i}(1-p)^{n-i}$$

여기서 $p$는 성공의 확률이고 함수는 $n$개의 독립 실험의 수열에서 성공 횟수의 이산 확률 분포를 나타내고, $\lfloor k\rfloor$는 $k$ 아래의 "바닥", 즉, $k$보다 작거나 같은 최대 정수입니다.

Derived functions

Complementary cumulative distribution function (tail distribution)

때때로, 반대 질문을 연구하고 확률 변수가 특정 수준보다 위의(above) 빈도를 묻는 것이 유용합니다. 이를 여 누적 분포 함수(complementary cumulative distribution function, 줄여서 ccdf) 또는 간단히 꼬리 분포(tail distribution) 또는 초과(exceedance)라고 불리고, 다음과 같이 정의됩니다: $${\bar {F}}_{X}(x)=\operatorname {P} (X>x)=1-F_{X}(x).$$

이것은 예를 들어 통계적 가설 테스트(hypothesis testing)에서 응용을 가지는데, 왜냐하면 한-측 p-값(p-value)은 적어도 관찰된 것만큼 극단적인 테스트 통계를 관찰할 확률이기 때문입니다. 따라서, 테스트 통계량(test statistic), T가 연속 분포를 가진다는 조건으로 하여, 한-측 p-값은 ccdf에 의해 간단하게 제공됩니다: 테스트 통계량의 관측된 값 $t$에 대해 $$p=\operatorname {P} (T\geq t)=\operatorname {P} (T>t)=1-F_{T}(t).$$

생존 분석(survival analysis)에서, ${\bar {F}}_{X}(x)$는 생존 함수(survival function)라고 불리고 $S(x)$로 표시되고, 반면 신뢰도 함수(reliability function)라는 용어는 공학에서 공통적입니다.

Properties

• 기대를 가지는 비-음의 연속 확률 변수에 대해, 마르코프의 부등식(Markov's inequality)은 다음임을 말합니다: $${\bar {F}}_{X}(x)\leq {\frac {\operatorname {E} (X)}{x}}.$$
• $x\to \infty$일 때, ${\bar {F}}_{X}(x)\to 0$이고, 사실은 $\operatorname {E} (X)$가 유한하다는 조건으로 하여 ${\bar {F}}_{X}(x)=o(1/x)$입니다.
  Proof:
  $X$가 밀도 함수 $f_{X}$를 가진다고 가정합니다, 임의의 $c>0$에 대해 $$\operatorname {E} (X)=\int _{0}^{\infty }xf_{X}(x)\,dx\geq \int _{0}^{c}xf_{X}(x)\,dx+c\int _{c}^{\infty }f_{X}(x)\,dx$$ 그런-다음, 다음임을 인식하고 $${\bar {F}}_{X}(c)=\int _{c}^{\infty }f_{X}(x)\,dx$$ 항들을 재-정렬하여, $$0\leq c{\bar {F}}_{X}(c)\leq \operatorname {E} (X)-\int _{0}^{c}xf_{X}(x)\,dx\to 0{\text{ as }}c\to \infty$$ 주장한 사실입니다.
• 기대를 가지는 확률 변수에 대해, $$\operatorname {E} (X)=\int _{0}^{\infty }{\bar {F}}_{X}(x)\,dx-\int _{-\infty }^{0}F_{X}(x)\,dx$$ 그리고 비-음의 확률 변수에 대해 두 번째 항이 0입니다.
  확률 변수가 비-음의 정수 값만 취할 수 있으면, 이것은 다음과 동등합니다: $$\operatorname {E} (X)=\sum _{n=0}^{\infty }{\bar {F}}_{X}(n).$$

Folded cumulative distribution

Example of the folded cumulative distribution for a normal distribution function with an expected value of 0 and a standard deviation of 1.

누적 분포 $F$의 그림은 종종 S와 같은 모양을 가지지만, 대안적인 설명은 그래프의 위쪽 절반을 접는 접힌 누적 분포(folded cumulative distribution) 또는 산 그림(mountain plot)입니다. 즉,

$F_{\text{fold}}(x)=F(x)1_{\{F(x)\leq 0.5\}}+(1-F(x))1_{\{F(x)>0.5\}}$

여기서 $1_{\{A\}}$는 지시 함수(indicator function)를 나타내고 두 번째 합하는 숫자는 생존 함수(survivor function)이므로, 하나는 오르막용이고 다른 하나는 내리막용으로 두 개의 스케일을 사용합니다. 이러한 형식의 설명은 중앙값, 산포도 (구체적으로, 중앙값으로부터 평균 절대 편차) 및 분포 또는 경험적 결과의 뾰족함(skewness)을 강조합니다.

Inverse distribution function (quantile function)

Main article: Quantile function

만약 CDF $F$가 엄격하게 증가하고 연속이면, $F^{-1}(p),p\in [0,1]$는 $F(x)=p$임을 만족하는 고유한 실수 $x$입니다. 이것은 역 분포 함수(inverse distribution function) 또는 분위-숫자 함수(quantile function)를 정의합니다.

일부 분포는 고유한 역을 가지지 않습니다 (예를 들어, 만약 모든 $a<x<b$에 대해 $f_{X}(x)=0$이면, $F_{X}$가 상수가 되는 원인이 됩니다). 이 경우에서, 다음과 같이 정의되는 일반화된 역 분포 함수(generalized inverse distribution function)를 사용할 수 있습니다:

$F^{-1}(p)=\inf\{x\in \mathbb {R} :F(x)\geq p\},\quad \forall p\in [0,1].$

• 예제 1: 중앙값은 $F^{-1}(0.5)$입니다.
• 예제 2: $\tau =F^{-1}(0.95)$라고 놓습니다. 그런-다음 $\tau$를 95번째 백분위수라고 부릅니다.

역 cdf의 몇 가지 유용한 속성 (역시 일반화된 역 분포 함수의 정의에서도 보존됨)은 다음입니다:

1. $F^{-1}$는 비-감소하는 것입니다.
2. $F^{-1}(F(x))\leq x$
3. $F(F^{-1}(p))\geq p$
4. $F^{-1}(p)\leq x$인 것과 $p\leq F(x)$인 것은 필요충분 조건입니다.
5. 만약 $Y$가 $U[0,1]$ 분포를 가지면 $F^{-1}(Y)$는 $F$로 분포됩니다. 이것은 역 변환 표본화(inverse transform sampling)-방법을 사용하여 무작위 숫자 생성(random number generation)에 사용됩니다.
6. 만약 $\{X_{\alpha }\}$가 같은 표본 공간 위에 정의된 독립적인 $F$-분포된 확률 변수의 모음이면, $Y_{\alpha }$가 $U[0,1]$로 분포되고 모든 $\alpha$에 대해 확률 1을 갖는 $F^{-1}(Y_{\alpha })=X_{\alpha }$임을 만족하는 확률 변수 $Y_{\alpha }$가 존재합니다.

cdf의 역은 균등 분포에 대해 얻은 결과를 다른 분포로 변환하기 위해 사용될 수 있습니다.

Empirical distribution function

경험적 분포 함수(empirical distribution function)는 표본에서 점을 생성한 누적 분포 함수의 추정입니다. 그것은 해당 놓여있는 분포에 확률 1로 수렴합니다. 경험적 분포 함수가 놓여있는 누적 분포 함수로 수렴의 율을 정량화하기 위한 많은 결과가 존재합니다.

Multivariate case

Definition for two random variables

둘 이상의 확률 변수를 동시에 다룰 때, 결합 누적 분포 함수(joint cumulative distribution function)도 정의될 수 있습니다. 예를 들어, 한 쌍의 확률 변수 $X,Y$에 대해, 결합 CDF $F_{XY}$는 다음에 의해 제공됩니다:

$$F_{X,Y}(x,y)=\operatorname {P} (X\leq x,Y\leq y)$$

(Eq.3)

여기서 오른쪽 변은 확률 변수 $X$가 $x$보다 작거나 같은 값을 취하고 $Y$가 $y$보다 작거나 같은 값을 가질 확률(probability)을 나타냅니다.

결합 누적 분포 함수의 예제:

두 개의 연속 변수 $X$와 $Y$에 대해: $$\Pr(a<X<b{\text{ and }}c<Y<d)=\int _{a}^{b}\int _{c}^{d}f(x,y)\,dy\,dx;$$

두 개의 이산 확률 변수에 대해, 확률 테이블을 생성하고 $X$와 $Y$의 각 잠재적 범위에 대한 누적 확률을 처리하는 것이 좋습니다. 예제는 다음과 같습니다:

테이블 형식에서 결합 확률 질량 함수가 주어지면, 결합 누적 분포 함수를 결정합니다.

	Y = 2	Y = 4	Y = 6	Y = 8
X = 1	0	0.1	0	0.1
X = 3	0	0	0.2	0
X = 5	0.3	0	0	0.15
X = 7	0	0	0.15	0

Solution: $X$와 $Y$의 각 잠재적 범위에 대해 주어진 확률의 테이블을 사용하여, 결합 누적 분포 함수는 다음 테이블 형식으로 구성될 수 있습니다:

	Y < 2	2 ≤ Y < 4	4 ≤ Y < 6	6 ≤ Y < 8	Y ≥ 8
X < 1	0	0	0	0	0
1 ≤ X < 3	0	0	0.1	0.1	0.2
3 ≤ X < 5	0	0	0.1	0.3	0.4
5 ≤ X < 7	0	0.3	0.4	0.6	0.85
X ≥ 7	0	0.3	0.4	0.75	1

Definition for more than two random variables

$N$개의 확률 변수 $X_{1},\ldots ,X_{N}$에 대해, 결합 CDF $F_{X_{1},\ldots ,X_{N}}$는 다음에 의해 제공됩니다:

$$F_{X_{1},\ldots ,X_{N}}(x_{1},\ldots ,x_{N})=\operatorname {P} (X_{1}\leq x_{1},\ldots ,X_{N}\leq x_{N})$$

(Eq.4)

$N$개의 확률 변수를 확률 벡터(random vector) $\mathbf {X} =(X_{1},\ldots ,X_{N})^{T}$로 적분하면 더 짧은 표기법을 산출합니다: $$F_{\mathbf {X} }(\mathbf {x} )=\operatorname {P} (X_{1}\leq x_{1},\ldots ,X_{N}\leq x_{N})$$

Properties

모든 각 다변수 CDF는 다음과 같습니다:

1. 각 변수에 대해 단조적으로 비-감수하는 것입니다,
2. 각 변수에 대해 오른쪽-연속입니다,
3. $0\leq F_{X_{1}\ldots X_{n}}(x_{1},\ldots ,x_{n})\leq 1,$
4. $$\lim _{x_{1},\ldots ,x_{n}\rightarrow +\infty }F_{X_{1}\ldots X_{n}}(x_{1},\ldots ,x_{n})=1{\text{ and }}\lim _{x_{i}\rightarrow -\infty }F_{X_{1}\ldots X_{n}}(x_{1},\ldots ,x_{n})=0,{\text{for all }}i.$$

위의 네 가지 속성을 만족하는 모든 각 함수가 단일 차원의 경우와 달리 다변수 CDF인 것은 아닙니다. 예를 들어, $x<0$ 또는 $x+y<1$ 또는 $y<0$에 대해 $F(x,y)=0$라고 놓고, 그렇지 않으면 $F(x,y)=1$라고 놓습니다. 위의 조건이 충족됨을 쉽게 알 수 있고, 여전히 $F$는 CDF가 아닌데 왜냐하면 만약 그렇다면 아래에 설명된 대로 ${\textstyle \operatorname {P} \left({\frac {1}{3}}<X\leq 1,{\frac {1}{3}}<Y\leq 1\right)=-1}$이기 때문입니다.

점이 초-직사각형(hyperrectangle)에 속할 확률은 일-차원 경우와 유사합니다:$$F_{X_{1},X_{2}}(a,c)+F_{X_{1},X_{2}}(b,d)-F_{X_{1},X_{2}}(a,d)-F_{X_{1},X_{2}}(b,c)=\operatorname {P} (a<X_{1}\leq b,c<X_{2}\leq d)=\int ...$$

Complex case

Complex random variable

$P(Z\leq 1+2i)$ 형식의 표현이 의미가 없기 때문에 실수 확률 변수에서 복소 확률 변수(complex random variables)로의 누적 분포 함수의 일반화는 명확하지 않습니다. 어쨌든, $P(\Re {(Z)}\leq 1,\Im {(Z)}\leq 3)$ 형식의 표현은 의미가 있습니다. 그러므로, 실수 부분과 허수 부분의 결합 분포(joint distribution)를 통해 복소 확률 변수의 누적 분포를 정의합니다: $$F_{Z}(z)=F_{\Re {(Z)},\Im {(Z)}}(\Re {(z)},\Im {(z)})=P(\Re {(Z)}\leq \Re {(z)},\Im {(Z)}\leq \Im {(z)}).$$

Complex random vector

Eq.4의 일반화는 복소 확률 벡터 $\mathbf {Z} =(Z_{1},\ldots ,Z_{N})^{T}$의 CDS에 대한 정의로 다음과 같이 산출됩니다: $$F_{\mathbf {Z} }(\mathbf {z} )=F_{\Re {(Z_{1})},\Im {(Z_{1})},\ldots ,\Re {(Z_{n})},\Im {(Z_{n})}}(\Re {(z_{1})},\Im {(z_{1})},\ldots ,\Re {(z_{n})},\Im {(z_{n})})=\operatorname {P} (\Re {(Z_{1})}\leq \Re {(z_{1})},\Im {(Z_{1})}\leq \Im {(z_{1})},\ldots ,\Re {(Z_{n})}\leq \Re {(z_{n})},\Im {(Z_{n})}\leq \Im {(z_{n})})$$

Use in statistical analysis

누적 분포 함수의 개념은 통계적 분석에서 두 가지 (유사한) 방법으로 명시적으로 나타납니다. 누적 빈도 분석(Cumulative frequency analysis)은 참조 값보다 작은 현상의 값의 발생 빈도를 분석하는 것입니다. 경험적 분포 함수(empirical distribution function)는 간단한 통계적 속성이 유도될 수 있고 다양한 통계적 가설 테스트(statistical hypothesis tests)의 기초를 형성할 수 있는 누적 분포 함수의 형식적인 직접 추정입니다. 그러한 테스트는 주어진 분포에서 발생한 데이터 표본에 대한 증거가 있는지, 또는 같은 (알려지지 않은) 모집단 분포에서 발생한 데이터의 두 표본에 대한 증거가 있는지 여부를 평가할 수 있습니다.

Kolmogorov–Smirnov and Kuiper's tests

콜모고로프–스미르노프 테스트(Kolmogorov–Smirnov test)는 누적 분포 함수를 기반으로 하고 두 개의 경험적 분포가 다른지 여부 또는 경험적 분포가 이상적인 분포와 다른지 여부를 테스트하기 위해 사용될 수 있습니다. 밀접하게 관련된 카이퍼의 테스트(Kuiper's test)는 분포의 도메인이 요일과 같이 순환하는 경우에 유용합니다. 예를 들어 카이퍼의 테스트는 토네이도의 수가 연중 변하는지 또는 제품 판매가 요일 또는 날짜에 따라 변하는지 확인하기 위해 사용될 수 있습니다.

See also

• Descriptive statistics
• Distribution fitting
• Ogive (statistics)
• Modified half-normal distribution with the pdf on $(0,\infty )$ is given as $f(x)={\frac {2\beta ^{\frac {\alpha }{2}}x^{\alpha -1}\exp(-\beta x^{2}+\gamma x)}{\Psi {\left({\frac {\alpha }{2}},{\frac {\gamma }{\sqrt {\beta }}}\right)}}}$, where $\Psi (\alpha ,z)={}_{1}\Psi _{1}\left({\begin{matrix}\left(\alpha ,{\frac {1}{2}}\right)\\(1,0)\end{matrix}};z\right)$ denotes the Fox-Wright Psi function.

External links

• Media related to Cumulative distribution functions at Wikimedia Commons