Jump to content

Exterior angle theorem

This is a fully translated article. Click here for more information.
From DawoumWiki, the free Mathematics self-learning
Original article: w:Exterior angle theorem

외부 각도 정리(exterior angle theorem)는 삼각형(triangle)의 외부 각도(exterior angle) 측정이 떨어져 있는 내부 각도 측정 중 하나보다 크다는 유클리드 원론(Euclid's Elements)의 제안 1.16입니다. 이것은 그것의 증명이 평행 공준(parallel postulate)에 의존하지 않기 때문에 절대 기하학(absolute geometry)에서 근본적인 결과입니다.

여러 학교에서 기하학을 다루면서, "외부 각도 정리"라는 용어는 다른 결과, 즉 삼각형의 외부 각의 측정이 떨어져 있는 내부 각도의 측정의 합과 같다는 제안 1.32의 부분에 적용되었습니다.[1] 유클리드의 평행 공준에 의존하는 이 결과는 유클리드의 외부 각도 정리와 구별하기 위해 "학교 외부 각도 정리"라고 참조될 것입니다.

일부 저자들은 외부 각도 정리의 강한 형태로 "학교 외부 각도 정리"를, 약한 형태로 "유클리드의 외부 각도 정리"를 언급합니다.[2]

Exterior angles

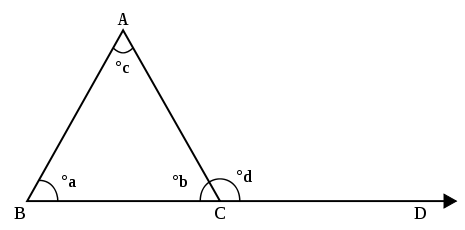
삼각형은 꼭짓점(vertices)이라고 하는 세 개의 모서리를 가집니다. 꼭짓점에서 함께 모인 삼각형의 변 (선분)은 두 개의 각도를 이룹니다 (삼각형의 변을 선분 대신 직선으로 고려하면 네 개의 각도를 이룹니다).[3] 이들 각도 중 하나만 그것의 내부에 삼각형의 세 번째 변을 포함하고, 이 각도는 삼각형의 내부 각도(interior angle)라고 불립니다.[4] 아래 그림에서 각 ∠ABC, ∠BCA, 및 ∠CAB는 삼각형의 세 내각입니다. 외부 각도(exterior angle)는 삼각형의 변 중 하나를 확장함으로써 형성됩니다; 연장된 변과 다른 변 사이의 각도가 외부 각도입니다. 그림에서, 각도 ∠ACD는 외부 각도입니다.

Euclid's exterior angle theorem

유클리드에 의해 제시된 제안 1.16의 증명은 종종 유클리드가 결함 있는 증명을 제공하는 한 곳으로 인용됩니다.[5][6][7]

유클리드는 외부 각도 정리를 다음과 같이 입증합니다:

  • 선분 AC의 중간 점 E를 구성합니다(construct),
  • 반직선(ray) BE를 그립니다,
  • E가 (역시) B와 F의 중간점이 되도록 반직선 BE 위에 점 F를 구성합니다,
  • 선분 FC를 그립니다.

합동(congruent) 삼각형에 의해, 우리는 ∠ BAC = ∠ ECF이고 ∠ ECF가 ∠ ECD보다 작고, ∠ ECD = ∠ ACD이므로 ∠ BAC는 ∠ ACD보다 작고 같은 것은 각도 ∠ CBA에 대해 BC를 이등분함으로써 수행될 수 있습니다.

결함은 점 (위의, F)이 "내부" 각도 (∠ ACD)에 놓인다는 가정에 있습니다. 이 주장에 대한 이유는 제공되지 않지만, 동반된 다이어그램을 보면 그것이 사실인 것처럼 보입니다. 유클리드 기하학에 대한 완전한 공리의 집합이 사용될 때 (기하학의 토대(Foundations of geometry)를 참조), 이 유클리드 주장은 입증될 수 있습니다.[8]

Invalidity in spherical geometry

Small triangles may behave in a nearly Euclidean manner, but the exterior angles at the base of the large triangle are 90°, a contradiction to the Euclid's exterior angle theorem.

외부 각도 정리는 구형 기하학(spherical geometry)에서 유효하지 않고 관련된 타원 기하학(elliptical geometry)에서도 유효하지 않습니다. 그것의 꼭짓점 중 하나가 북극(North Pole)에 있고 다른 두 꼭짓점이 적도(equator)에 놓이는 구형 삼각형(spherical triangle)을 생각해 보십시오. 북극에서 나오는 삼각형의 변 (구의 큰 원)은 모두 적도와 직각을 이루므로, 이 삼각형은 떨어져 있는 내부 각도와 같은 외부 각도를 가집니다. (북극에서) 다른 내부 각도는 90°보다 크게 만들 수 있으며, 이 명제의 실패를 더욱 강조합니다. 어쨌든, 유클리드의 외부 각도 정리는 절대 기하학(absolute geometry)의 정리이므로, 그것은 쌍곡선 기하학(hyperbolic geometry)에서는 자동으로 유효합니다.

High school exterior angle theorem

학교 외부 각도 정리 (SEAT)는 삼각형의 한 꼭짓점에서 외부 각도의 크기가 삼각형의 다른 두 꼭짓점에서 내부 각도 (떨어져 있는 내부 각도)의 크기의 합과 같다고 말합니다. 따라서, 그림에서, 각도 ACD의 크기는 각도 ABC의 크기 더하기 각도 CAB의 크기와 같습니다.

SEAT는 삼각형의 각도의 합(sum of angles of a triangle)이 180°라는 유클리드 명제와 논리적으로 동등(logically equivalent)합니다. 만약 삼각형에서 각도의 측정의 합이 180°이라고 알려져 있으면, SEAT는 다음과 같이 입증됩니다:

다른 한편으로, 만약 SEAT가 참 명제로 취해지면, 다음과 같이 됩니다:

Illustration of proof of the HSEAT

삼각형의 각도의 측정의 합이 180°임을 입증합니다.

SEAT의 유클리드 증명 (및 동시에 삼각형의 각도의 합에 대한 결과)은 점 C를 통과하는 변 AB에 평행한 직선을 구성하고 그런-다음 그림에서와 같은 결론을 얻기 위해 평행 직선의 해당 각도와 교대 내부 각도의 속성을 사용함으로써 시작합니다. 그림과 같이 결론을 얻습니다.[9]

SEAT는 삼각형에서 알 수 없는 각도의 측정을 계산하려고 시도할 때 극단적으로 유용할 수 있습니다.

Notes

  1. ^ Henderson & Taimiņa 2005, p. 110
  2. ^ Wylie 1964, p. 101 & p. 106
  3. ^ One line segment is considered the initial side and the other the terminal side. The angle is formed by going counterclockwise from the initial side to the terminal side. The choice of which line segment is the initial side is arbitrary, so there are two possibilities for the angle determined by the line segments.
  4. ^ This way of defining interior angles does not presuppose that the sum of the angles of a triangle is 180 degrees.
  5. ^ Faber 1983, p. 113
  6. ^ Greenberg 1974, p. 99
  7. ^ Venema 2006, p. 10
  8. ^ Greenberg 1974, p. 99
  9. ^ Heath 1956, Vol. 1, p. 316

References

  • Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1
  • Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN 0-7167-0454-4
  • Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications.
(3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3).
  • Henderson, David W.; Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.), Pearson/Prentice-Hall, ISBN 0-13-143748-8
  • Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3
  • Wylie, C. R. Jr. (1964), Foundations of Geometry, New York: McGraw-Hill

HSEAT references

  • Geometry Textbook - Standard IX, Maharashtra State Board of Secondary and Higher Secondary Education, Pune - 411 005, India.
  • Geometry Common Core, 'Pearson Education: Upper Saddle River, ©2010, pages 171-173 | United States.
  • Wheater, Carolyn C. (2007), Homework Helpers: Geometry, Franklin Lakes, NJ: Career Press, pp. 88–90, ISBN 978-1-56414-936-7.

Retrieved from "https://dawoum.duckdns.org/w/index.php?title=Exterior_angle_theorem&oldid=70123"