Fundamental polygon
수학(mathematics)에서, 기본 다각형(fundamental polygon)은 0보다 큰 지너스의 모든 각 컴팩트 리만 표면(compact Riemann surface)에 대해 정의될 수 있습니다. 그것은 기본 그룹(fundamental group)을 통해 표면의 토폴로지를 인코딩할 뿐만 아니라 등각 동등성까지 리만 표면을 결정합니다. 균등화 정리(uniformization theorem)에 의해, 모든 각 컴팩트 리만 표면은 다음 중 정확히 하나에 의해 주어지는 단순히 연결된 보편 덮는 표면을 가집니다:
- 리만 구(Riemann sphere),
- 복소 평면(complex plane),
- 단위 디스크 D 또는 동등하게 위쪽 절반-평면 H.
지너스 영의 첫 번째 경우에서, 표면은 리만 구와 등각적으로 동등합니다.
지너스 일의 두 번째 경우에서, 표면은 C에서 일부 격자 Λ에 대해 토러스 C/Λ와 등각적으로 동등합니다. Λ의 기본 다각형은, 만약 볼록하다고 가정되면, 주기 평행사변형 또는 중심적으로 대칭 육각형으로 취할 수 있으며, 1891년 페도로프(Fedorov)에 의해 처음으로 입증된 결과입니다.
지너스 g > 1의 마지막 경우에서, 리만 표면은 Γ가 뫼비우스 변환(Möbius transformations)의 푹스 그룹(Fuchsian group)인 H/Γ와 등각적으로 동등합니다. Γ에 대한 기본 도메인은 H 위의 쌍곡선 메트릭에 대한 볼록 다각형에 의해 제공됩니다. 이것들은 디리클레 다각형으로 정의될 수 있고 짝수의 변을 가집니다. 기본 그룹 Γ의 구조는 그러한 다각형에서 읽을 수 있습니다. 준등각 매핑(quasiconformal mappings)의 이론과 벨트라미 방정식(Beltrami equation)을 사용하여, 프리케(Fricke)에 의해 처음 정의된 4g 변을 갖는 정식의 볼록 디리클레 다각형이 있음을 표시할 수 있으며, 이는 2g 생성기 a1, b1, a2, b2, ..., ag, bg와 단일 관계 [a1,b1][a2,b2] ⋅⋅⋅ [ag,bg] = 1를 갖는 그룹으로 Γ의 표준 표현에 해당하며, 여기서 [a,b] = a b a−1b−1입니다.
방향화된 닫힌 2-매니폴드 M 위의 임의의 리만 메트릭은 M 위의 복소 구조를 정의하여, M을 컴팩트 리만 표면으로 만듭니다. 기본 다각형의 사용을 통해, 2개의 방향화된 닫힌 2-매니폴드는 그것의 지너스, 즉, 아벨 그룹 Γ/[Γ,Γ]의 랭크의 절반에 따라 분류됨이 따라오며, 여기서 Γ = π1(M)입니다. 더욱이, 그것은 역시 두 개의 컴팩트 리만 표면이 미분동형적인 것과 그것들이 위상동형적인 것은 필요충분 조건이라는 준등각 매핑의 이론으로부터 이어집니다. 결과적으로, 2개의 닫힌 방향화된 2-매니폴드가 위상동형적인 것과 그것들이 미분동형적인 것은 필요웅분 조건입니다. 그러한 결과는 역시 미분 토폴로지(differential topology)의 방법을 사용하여 입증될 수 있습니다.[1][2]
Fundamental polygons in genus one


Parallelograms and centrally symmetric hexagons
지너스 일의 경우에서, 기본 볼록 다각형은 R2 = C 위에 Λ = Z a ⊕ Z b의 변환에 의해 동작에 대해 찾으며, 여기서 a와 b는 R에 걸쳐 선형적으로 독립적입니다. (R2 위에 실수 선형 변환을 수행한 후, 필요하다면 Λ = Z2 = Z + Z i라고 가정될 수 있습니다; 지너스 일 리만 표면에 대해, Im ω > 0를 갖는 Λ = Z2 = Z + Z ω 형식을 가지도록 취할 수 있습니다.) 기본 도메인(fundamental domain)은 0 < s , t < 1에 대해 평행사변형 s x + t y로 제공되며, 여기서 x와 y는 Λ의 생성기입니다.
만약 C가 기본 볼록 다각형의 내부이면, x가 Λ에 걸쳐 실행할 때 평행이동 C + x는 R2를 덮습니다. 따라서 C의 경계점은 교차점 C ∩ (C + x)으로 형성됩니다. 이것들은 ∂C에서 컴팩트 볼록 집합이고 따라서 C의 꼭짓점 또는 C의 변 중 하나입니다. 따라서 C의 모든 각 닫힌 변은 이런 법으로 쓸 수 있습니다. −x만큼 평행이동하면 C ∩ (C − x)도 C의 변이 됨이 따라옵니다. 따라서 C의 변은 같은 길이의 평행한 쌍으로 나타납니다. 같은 길이의 두 평행 선분의 끝점은 그것들이 교차하고 교차점이 끝점을 연결하는 선분의 중간점에서 발생하도록 연결될 수 있습니다. 따라서, 모든 그러한 선분의 교차점은 같은 점에서 발생합니다. 해당 점을 원점으로 평행이동하여, 다각형이 중심적으로 대칭임이 따라옵니다; 즉, 점 z가 다각형에 있으면 −z도 마찬가지입니다.
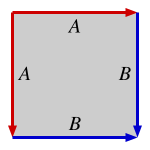
중심적으로 대칭 볼록 육각형의 평행이동이 평면을 테셀레이션하는 것을 쉽게 볼 수 있습니다. 만약 A가 육각형의 한 점이면, 격자는 변위 벡터 AB와 AC에 의해 생성되며, 여기서 B와 C는 A의 이웃도 아니고 A의 반대편도 아닌 두 꼭짓점입니다. 실제로 두 번째 그림은 육각형이 선분 AB와 AC로 잘라낸 두 삼각형을 변위시킴으로써 얻은 평행사변형과 동등합니다. 마찬가지로 첫 번째 그림은 평행사변형에 의한 타일링을 육각형 타일링과 일치시키는 또 다른 방법을 보여줍니다. 만약 육각형의 중심이 0이고 꼭짓점이 순서대로 a, b, c, −a, −b, 및 −c이면, Λ는 생성기 a + b와 b + c를 갖는 아벨 그룹입니다.
Examples of Fundamental Polygons Generated by Parallelograms
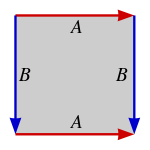
다양한 방법으로 마름모(rhombus)의 변을 식별함으로써 만들 수 있는 정확히 네 가지 토폴로지가 있습니다. 그것들은 AABB 또는 ABAB 순서열로 정사각형 위의 방향화된 가장자리 A와 B로 아래에 제공됩니다.
| Name | Sphere | Torus | Projective plane | Klein bottle |
|---|---|---|---|---|
| Orientable | Yes | No | ||
| Total curvature | 4π | 0 | 2π | 0 |
| Topology ABAB (square) |
 |
 |
 (or ) | |
| Topology AABB (square) |
 [3] |
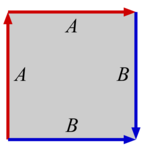 (or ) |
 | |
| Geometry |  Sphere |
 Torus |
 Hemisphere |
 Half torus |
Fedorov's theorem
1891년 러시아 결정학자 이그라프 페도로프(Evgraf Fedorov)가 확립된 페도로프의 정리는 평행사변형과 중심적으로 대칭 육각형이 기본 도메인인 유일한 볼록 다각형이라고 주장합니다.[4] 이것에 대한 몇 가지 증명이 있으며, 볼록성 이론(convexity theory), 숫자의 기하학(geometry of numbers), 및 브룬-민코프스키 부등식(Brunn–Minkowski inequality)과 같은 원 채우기(circle packing)의 결과와 관련된 최근의 증명이 있습니다.[5] 콕서터와 보로노이로 인한 두 가지 기본적인 증명이 여기에서 제시될 것입니다.[6][7]
콕서터의 증명은 2m 변을 갖는 중앙적으로 대칭 볼록 다각형 C가 있다고 가정함으로써 진행합니다. 그런-다음 N2 기본 평행사변형으로부터 형성된 큰 닫힌 평행사변형은 큰 평행사변형의 가장자리를 넘어 이동하는 C의 평행이동에 의해 타일링됩니다. 이것은 토러스 C/NΛ에 타일링을 유도합니다. v, e, 및 f를 이 타일링에서 꼭짓점, 가장자리, 및 면의 개수라고 놓습니다 (몫 공간에서 식별을 고려함). 그런-다음 토러스의 오일러-푸앵카레 특성(Euler–Poincaré characteristic)이 0이기 때문에,
다른 한편으로, 각 꼭짓점은 적어도 3개의 서로 다른 가장자리 위에 있고 모든 각 가장자리는 두 정점 사이에 있으므로,
게다가, 모든 각 가장자리는 정확히 두 면 위에 있기 때문에,
따라서,
이때, 요구된 것처럼,
보로노이(Voronoi)의 증명은 C의 모든 각 가장자리가 Λ의 원소 x에 해당한다는 관찰에서 시작됩니다. 실제로 가장자리는 0에서 x까지 반지름의 직교 이등분선입니다. 따라서 0에서 각 가장자리까지의 수직선의 발은 각 가장자리의 내부에 놓입니다. 만약 y가 임의의 격자 점이면, 1/2 y는 C 안에 놓일 수 없습니다; 그렇다면, -1/2 y도 C 안에 있을 것이고, C가 Λ의 기본 도메인인 것과 모순됩니다. ±x1, ..., ±xm을 C의 변에 해당하는 Λ의 2m 구별되는 점이라고 놓습니다. Λ의 생성기 a와 b를 고정합니다. 따라서 xi = αi a + βi b이며, 여기서 αi와 βi는 정수입니다. αi와 βi가 모두 짝수일 수는 없습는데, 왜냐하면 그렇지 않으면 ± 1/2 xi가 변 위에 Λ의 점이 될 것이기 때문에, 이는 C가 기본 도메인이 되는 것과 모순됩니다. 따라서 정수 쌍 (αi, βi) 모듈로 2에 대해 세 가지 가능성: (0,1), (1,0), 및 (1,1)가 있습니다. 결과적으로, 만약 m > 3이면, xi − xj의 두 좌표가 짝수인 i ≠ j를 갖는 xi와 xj가 있을 것이며, 즉, 1/2 (xi + xj)는 Λ에 놓입니다. 그러나, 이것은 가장자리의 두 내부 점을 연결하는 선분의 중간점이고 따라서 다각형의 내부, C 안에 놓입니다. 이것은 다시 C가 기본 도메인이라는 사실과 모순됩니다. 따라서 reductio ad absurdum m ≤ 3이며, 주장한 대로 입니다.
Dirichlet–Voronoi domains
C = R2에서 격자 Λ에 대해, 기본 도메인은 C의 등각 구조를 사용하여 정식적으로 정의될 수 있습니다. C의 등각 변환 그룹은 a ≠ 0을 갖는 복소 아핀 변환 g(z) = az + b에 의해 제공됩니다. 이들 변환은 인수까지 유클리드 메트릭 d(z, w) = |z − w|을 보존하고 마찬가지로 방향(orientation)을 보존합니다. 그것은 ∞에 점을 고정하는 뫼비우스 그룹의 부분그룹입니다. 메트릭 구조는 C = {z: d(z, 0) < d(z, λ) for all λ ≠ 0 in Λ}에 의해 정식의 기본 도메인을 정의하기 위해 사용될 수 있습니다. (기본 도메인이라는 것은 정의에서 명백합니다.) 이것은 디리클레 도메인(Dirichlet domain) 또는 보로노이 다이어그램(Voronoi diagram)의 예입니다: 복소 평행이동이 아벨 그룹을 형성하므로, Λ의 동작으로 교환하기 때문에, 이들 개념이 일치합니다. Im ω > 0를 갖는 Λ = Z + Zω에 대한 정식의 기본 도메인은 대칭적으로 볼록 평행사변형 또는 중심 0을 갖는 육각형입니다. 등각 동등성에 의해, 주기 ω는 |Re ω| ≤ 1/2와 |ω| ≥ 1를 만족시키도록 더 제한될 수 있습니다. 디리클레(Dirichlet)가 보여준 것처럼 ("디리클레의 육각형 정리", 1850), 거의 모든 ω에 대해 기본 도메인은 육각형입니다. Re ω > 0에 대해, 변의 중간점은 ±1/2, ±ω/2, 및 ±(ω – 1)/2로 지정됩니다; 변은 0에서 해당 반지름을 직각으로 이등분하여, 꼭짓점을 완전하게 결정합니다. 사실 첫 번째 꼭짓점은 실수 x와 y를 갖는 (1 + ix)/2 와 ω(1 + iy)/2 형식을 가져야 합니다; 따라서, ω = a + ib이면, a – by = 1이고 x = b + ay입니다. 따라서 y = (a – 1)/b와 x = (a2 + b2 – a)/b입니다. 따라서 6개의 꼭짓점은 ±ω(1 – iy)/2와 ±(1 ± ix)/2입니다.[8]
Fundamental polygons in higher genus
Overview
모든 각 컴팩트 리만 표면 X는 단순하게 연결된 리만 표면 X인 보편 덮는 표면(universal covering surface)을 가집니다. X의 기본 그룹(fundamental group)은 X의 피복 변환(deck transformations)으로 동작하고 X의 이중정칙형(biholomorphisms)의 그룹의 부분그룹 Γ로 식별될 수 있습니다. 따라서 그룹 Γ는 X로 식별될 수 있는 컴팩트 몫 공간 X/Γ로 X 위에 자유롭게 동작합니다. 따라서 컴팩트 리만 표면의 분류는 가능한 그룹 Γ의 연구로 축소될 수 있습니다. 균등화 정리(uniformization theorem)에 의해, X는 리만 구, 복소 평면 또는 단위 디스크/위쪽 절반평면입니다. 컴팩트 리만 표면의 첫 번째 중요한 불변은 아벨 그룹 Γ/[Γ, Γ] (호몰로지 그룹(homology group) H1(X, Z)로 식별될 수 있음) 랭크의 절반에 의해 제공되는 토폴로지적 불변, 그것의 지너스(genus)입니다. 지너스는 덮는 공간이 리만 구이면 영; 그것이 복소 평면이면 일; 및 그것이 단위 디스크 또는 위쪽 절반 평면이면 일보다 큽니다.[9]
리만 구의 이중정칙형은 복소 뫼비우스 변환일 뿐이고 모든 각 비-항등 변환은 해당 복소수 행렬이 항상 적어도 하나의 비-영 고유벡터를 가지므로 적어도 하나의 고정점을 가집니다. 따라서, X가 리만 구이면, X는 리만 구에 단순 연결된 것이고 이중정칙적이어야 하며, 지너스 영 리만 표면입니다. X가 복소 평면일 때, 이중정칙형의 그룹은 아핀 그룹, ∞를 고정하는 복소 뫼비우스 변환이므로, a ≠ 0를 갖는 변환 g(z) = az + b입니다. 고정점 없이 비-항등 변환은 a = 1와 b ≠ 0을 갖는 변환, 즉, 비-영 평행이동입니다. 따라서 그룹 Γ은 지너스 일의 기본 다각형 위에 섹션에서 설명된 대로 몫 C/Λ를 갖는 C와 X에서 격자 Λ로 식별될 수 있습니다. X가 단위 디스크 또는 위쪽 절반 평면인 세 번째 경우에서, 이중정칙형의 그룹은 단위 원 또는 실수 축을 고정하는 복소 뫼비우스 변환으로 구성됩니다. 전자의 경우에서, 변환은 그룹 SU(1, 1)/{±I}의 원소에 해당합니다; 후자의 경우에서 그것들은 실수 뫼비우스 변환에 해당하므로, SL(2, R)/{±I}의 원소입니다.[9]
컴팩트 몫—첫 번째 종류의 폭스 그룹(Fuchsian group)—을 갖는 단위 디스크 또는 위쪽 절반 평면 위에 자유롭게 동작하는 가능한 그룹 Γ의 연구와 분류는 아래에 설명된 대로 그것들의 기본 다각형을 연구함으로써 수행될 수 있습니다. 푸앵카레(Poincaré)가 관찰한 것처럼, 각각의 그러한 다각형은 특별한 속성을 가지며, 즉, 그것들은 볼록하고 변 사이에 자연스러운 쌍화를 가집니다. 이것들은 그룹을 복구할 수 있게 할 뿐만 아니라 생성기와 관계에 의해 그룹의 명시적 표시를 제공합니다. 반대로 푸앵카레는 임의의 그러한 다각형이 컴팩트 리만 표면을 생성한다는 것을 입증했습니다; 사실, 푸앵카레의 다각형 정리는 다각형이 이상적인 꼭짓점을 가질 수 있는 보다 일반적인 다각형에 적용되었지만, 그의 증명은 그러한 꼭짓점 없이 컴팩트 경우에만 완전했습니다. 다각형의 볼록성에 대한 가정 없이, 지겔(Siegel)의 아이디어를 기반으로 Maskit과 de Rham에 의해 완전한 증명이 제공되었고, Beardon (1983), Iversen (1992), 및 Stillwell (1992)에서 찾을 수 있습니다. 카라테오도리(Carathéodory)는 슈바르츠 삼각형(Schwarz triangles)에 의한 테셀레이션, 즉, 각도 π/a, π/b, π/c의 합이 π보다 작은 측지선 삼각형에 의한 타일링의 존재에 대한 기본적인 처리를 제공했으며, 여기서 a, b, c는 정수입니다. 모든 각도가 π/2g와 같을 때, 이것은 정규 4g-변 쌍곡선 다각형에 의한 타일링을 설정하고 따라서 몫 공간으로서 지너스 g의 특정 컴팩트 리만 표면의 존재를 설정합니다. 이중정칙적 대칭의 순환 그룹 Z2g를 가지는 이 특별한 예제는 아래의 개발에 사용됩니다.[9]
컴팩트 리만 표면의 위상동형과 미분동형까지 분류는 위상동형과 미분동형까지 닫힌 방향-가능(orientable) 2-매니폴드의 분류를 의미합니다: 같은 지너스를 갖는 임의의 두 개의 2-매니폴드는 미분동형적입니다. 사실 단일의 분할을 사용하여, 모든 각 닫힌 방향-가능 2-매니폴드는 리만 메트릭(Riemannian metric)을 허용합니다. 컴팩트 리만 표면에 대해, 등각 메트릭이 정칙 좌표에서 매트릭이 형식 ρ(z) |dz|2을 취하도록 등각적으로 도입될 수도 있습니다. 이 메트릭이 선택되면, 지역적 이중정칙적 매핑은 등각적인 정확하게 방향-보존하는 미분동형, 즉, 매끄러운 함수에 의한 메트릭을 스케일합니다. 라플라스 또는 벨트라미 방정식에 대한 지역적 존재 정리를 사용하여 입증될 수 있는 등온 좌표(isothermal coordinates)의 존재는 모든 각 닫힌 방향화된 리만 2-매니폴드가 그것의 메트릭과 호환되는 복소 구조를 제공할 수 있고, 따라서 컴팩트 리만 표면의 구조를 가질 수 있음을 보여줍니다. 이 구성은 미분동형 또는 위상동형까지 닫힌 방향-가능 2-매니폴드의 분류가 컴팩트 리만 표면의 경우로 축소될 수 있음을 보여줍니다.[10]
컴팩트 리만 표면의 위상동형과 미분이형까지 분류는 기본 다각형을 사용하여 달성될 수 있습니다. 실제로, 푸앵카레가 관찰한 것처럼, 컴팩트 리만 표면 H/Γ에 대한 볼록 기본 다각형은 유클리드 공간에서 쌍곡선 공간으로 디리클레의 방법을 적용함으로써 구성될 수 있습니다. 그런-다음 Nevanlinna와 Jost에 따르면, 기본 도메인은 단계적으로 수정되어 꼭짓점이 Γ의 단일 궤도에 놓이고 조각-별 측지선 변에 놓이는 비-볼록 다각형을 생성할 수 있습니다. 변에 대한 쌍화 관계도 이들 각 단계에서 수정됩니다. 각 단계는 다각형의 내부의 대각선 측지선 구획으로 다각형을 자르고 쌍화화 관련된 뫼비우스 변환 중 하나를 사용하여 다각형을 재조립하는 것을 포함됩니다. 쌍을 이룬 두 변은 원래 관계와 유사한 속성을 만족시키는 최종 쌍화 관계에서 공통 꼭짓점을 가질 수 없습니다. 이 다각형은 내부에서 대각선 조각-별 측지선 구획으로 절단한 후 다각형을 재조립함으로써 차례로 연속적으로 수정될 수 있습니다. 최종 다각형은 조각별 측지선인 변을 갖는 4g 동등한 꼭짓점을 가집니다. 변은 쌍을 이룬 변에 뫼비우스 변환을 제공하는 그룹 원소로 레이블-지정됩니다. 순서대로 라벨링은 다음과 같습니다:
이때 Γ는 다음과 같은 단일 관계에 따라 ai와 bi에 의해 생성되도록 합니다:
-
Genus zero surface (sphere)
-
Genus one surface (torus)
-
Genus two surface
-
Genus three surface
교차 숫자(intersection numbers)의 이론을 사용하여, 측지선으로 꼭짓점을 연결함으로써 얻은 모양도 반드시 볼록하지 않은 적절한 다각형이고, 쌍화를 제공하는 같은 그룹 원소를 갖는 기본 도메인이라는 것이 따라옵니다. 이렇게 하면 측지선 구획에 의해 제공된 가장자리와 표준 레이블을 갖는 기본 다각형이 생성됩니다. 몫 그룹 Γ/[Γ, Γ], Γ의 아벨화는 2g 생성기를 갖는 자유 아벨 그룹입니다. 따라서 지너스(genus) g는 토폴로지적 불변입니다. 같은 지너스를 갖는 두 리만 표면이 4g-변의 다각형—클라인 모델(Klein model)의 유클리드 다각형—의 변을 쌍을 이루는 변 사이의 미분동형으로 식별함으로써 얻어지기 때문에 토폴로지적 공간으로서 위상동형적이라는 것을 쉽게 알 수 있습니다.[11] 이 구성을 정규 4g-변 다각형에 적용하면 리만 표면을 토폴로지에 대한 입문 텍스트에서 방향화된 표면의 표준 설명, g 구멍을 갖는 도넛으로 토폴로지적으로 볼 수 있습니다.[12][13]
몇 가지 추가 결과가 있습니다:
- 두 개의 위상동형적 리만 표면은 미분동형적입니다.
- 지너스 g에서 임의의 볼록 기본 다각형은 N 꼭짓점을 가지며, 여기서 4g ≤ N ≤ 12g – 6.
- 지너스 g에서 디리클레 다각형은 중심의 조밀한 열린 집합에 대해 정확하게 12g – 6 꼭짓점을 가집니다.
- 모든 각 지너스 g 리만 표면은 프리케 기본 다각형, 즉, 변 사이의 정식의 쌍화를 갖는 다각형을 가집니다. (다각형이 반드시 디리클레 다각형일 필요는 없습니다.)
- 기본 그룹의 생성기의 적절한 정규화와 레이블-지정 후, 프리케 다각형이 고유하게 결정되고 이를 설명하는 6g – 6 실수 매개변수는 지너스 g에서 타이히뮐러 공간(Teichmüller space)에 대한 전역적 실수 해석적 매개변수로 사용될 수 있습니다.
이들 결과는 위상동형과 기본 그룹 사이의 상호 관계와 밀접하게 관련이 있습니다: 이것은 리만 표면의 매핑 클래스 그룹—리만 표면 H/Γ 모듀로 그것들의 준-등각 자기-준동형의 그룹은 항등에 대한 호모토피적—이 Γ의 외부 자기동형 그룹 (Dehn–Nielsen–Baer 정리)으로 식별될 수 있다는 사실을 반영합니다.[14] 이 연결을 보기 위해, f가 X1 = H/Γ1를 X2 = H/Γ2 위로의 준-등각 위상동형이면, f는 H를 자체 위로의 준등각 위상동형 f로 상승합니다. 이 상승은 Γ1의 원소를 갖는 사전-합성과 Γ2의 원소를 갖는 사후-합성까지 고유합니다. 만약 πi가 H를 Xi 위로의 투영이면, f ∘ π1 = π2 ∘ f이고 Γi는 πi ∘ g = πi를 만족하는 H의 위상동형 g의 그룹일 뿐입니다. Γ1에서 g에 대해 f g = θ(g) f를 따르는 경우 θ는 Γ1를 Γ2 위로의 그룹 동형입니다. f의 다른 선택은 안의 자기동형을 갖는 합성에 의해 θ를 변경합니다: 그러한 동형은 동등한(equivalent) 것이라고 말합니다.[15]
두 개의 동형 θ와 θ′가 등동한 것과 대응하는 위상동형 f와 f'가 호모토픽적인 것은 필요충분 조건입니다. 사실, 표면의 준등각 자기-위상동형 f가 기본 그룹의 안의 자기동형인 것과 그것이 항등 맵에 호모토픽적인 것은 필요충분 조건임을 것으로 충분합니다: 다시 말해서, H/Γ를 Out Γ으로의 준등각 자기-위상동형 그룹의 준동형이 단사적인 매핑 클래스 그룹으로 전달됩니다. 실제로, 먼저 F(t)가 F(0) = id와 F(1) = f를 갖는 자체-위상동형의 연속적인 경로라고 가정합니다. 그런-다음 F(0) = id를 갖는 연속 상승 F(t)가 있습니다. 게다가, Γ에서 각 g에 대해, F(t) ∘ g ∘ F(t)−1는 t = 0에 대해 g와 같은 Γ의 연속적으로 변화하는 원소입니다; 따라서 Γ의 불연속성은 이 원소를 상수가 되도록 강제하고 따라서 F(t)가 Γ와 교환하다록 g와 같으므로, F(1)은 자명한 자기동형을 유도합니다. 만약 다른 한편으로 F가 Γ의 안의 자기동형을 유도하는 준등각 상승이면, 필요에 따라 원소 Γ로 합성한 후 F가 Γ로 교환한다고 가정될 수 있습니다. F는 준등각적이므로, Γ와도 교환하는 원의 준-대칭 위상동형으로 확장됩니다. Γ에서 각 g ≠ id는 쌍곡선이므로 모든 다른 점 z에 대해, g±n(z)는 n이 무한대로 경향일 때 a±로 경향임을 만족하는 원 a±에 두 개의 고정점을 가집니다. 따라서 F는 이들 점을 고정해야 합니다; 이들 점들은 g가 변화함에 따라 원에서 조밀하기 때문에, F가 단위 원을 고정된다는 것이 따라옵니다. μ = Fz / Fz라고 놓으며, 이때 μ는 Γ-불변 벨트라미 미분입니다. F(t)를 단위 원 위의 세 점을 고정하기 위해 정규화된 벨트라미 방정식 tμ의 해라고 놓습니다. 그런-다음 F(t)는 Γ와 교환하고, 따라서 F = F(1)에 대해, 단위 원의 항등식입니다. 구성에 의해 F(t)는 항등식과 F 사이의 아이소토리입니다. 이것은 단사성을 입증합니다.[15]
전사성의 증명은 D 위의 쌍곡선 메트릭과 Γ 위의 단어-길이 메트릭을 비교하는 데 의존합니다.[16] 일반성의 손실 없이 0이 볼록 기본 다각형 C의 내부에 있고 g가 Γ의 원소라고 가정하여, 0에서 g(0)로의 반직선—쌍곡선 측지선—은 C의 연속 평행이동을 통과합니다. 이들 각각은 Γ의 생성기 또는 (연속 평행이동이 꼭짓점에서 만나면) 생성기의 고정된 곱을 적용함으로써 이전 것에서 얻습니다. 따라서 0과 g(0) 사이의 쌍곡선 거리는 g의 단어 길이의 4g 배에 기본 다각형의 지름의 두 배를 더한 값보다 작습니다. 따라서 단어 길이 L(g)에 의해 정의되는 Γ 위에 메트릭 d1(g, h) = L(h−1g)은 양의 상수 a와 b에 대해 다음을 만족시킵니다:
반대로 다음임을 만족하는 상수 c와 d가 있습니다:
Dirichlet polygons
위쪽 절반-평면(upper half-plane) H에 있는 점 과 위쪽 절반-평면 위에 자유롭게 불연속적(freely discontinuously)으로 동작하는 PSL(2, R)의 구별되는 부분그룹(subgroup) Γ가 주어지면, 디리클레 다각형(Dirichlet polygon)을 다음 점의 집합으로 정의할 수 있습니다:
여기서, d는 위쪽 절반-평면 위의 쌍곡선 메트릭(metric)입니다. 메트릭 기본 다각형은 보통 디리클레 다각형(Dirichlet polygon)이라고 불립니다.
- 기본 다각형은 기본 도메인(fundamental domain)입니다.
- 이 기본 다각형은 다각형의 임의의 두 점을 연결하는 측지선(geodesic)이 다각형 내부에 전적으로 포함된다는 점에서 볼록(convex)입니다.
- F의 지름(diameter)은 H/Γ의 지름보다 작거나 같습니다. 특히, F의 클로저는 컴팩트입니다.
- 만약 Γ가 H에서 고정된 점을 가지지 않고 H/Γ가 컴팩트이면, F는 유한하게 많은 변을 가질 것입니다.
- 다각형의 각 변은 측지선(geodesic) 호입니다.
- 다각형의 모든 각 변 s에 대해, Γ에서 일부 g에 대해 gs = s′임을 만족하는 정확하게 하나의 다른 변 s′가 있습니다. 따라서, 이 다각형의 짝수 개의 변을 가질 것입니다.
- 변을 서로 연결하는 그룹 원소 g의 집합은 Γ의 생성기(generators)입니다 (이 생성기의 집합이 반드시 최소일 필요는 없음에 주목하십시오).
- 위쪽 절반-평면은 Γ의 동작 아래에서 F가 클로저에 의해 타일링됩니다. 즉, 이며 여기서 는 F의 클로저입니다.
Normalised polygon
이 섹션에서, 임의적인 디리클레 다각형에서 시작하여, Jost (2002)에서 정교화된 Nevanlinna (1953)의 방법에 대해 설명하며, 다각형을 4g 동등한 꼭짓점과 변에 대한 정식의 쌍화를 갖는 비-볼록 다각형으로 수정합니다. 이 처리는 Seifert & Threlfall (1934)에서 제시된 방향-가능 2-차원 다면체의 고전적 토폴로지적 분류의 해석적 짝입니다.
Fricke canonical polygon
일보다 큰 지너스 g의 리만 표면이 주어지면, 프리케(Fricke)는 또 다른 기본 다각형, 디리클레 다각형의 매우 특별한 예제인 프리케 정식의 다각형(Fricke canonical polygon)을 설명했습니다. 그 다각형은 표면의 기본 그룹의 표준 표현과 관련되어 있습니다. 프리케의 원래 구성은 복잡하고 Fricke & Klein (1897)에 설명되어 있습니다. Ahlfors와 Bers의 준등각 매핑의 이론을 사용하여, Keen (1965)은 프리케의 구성의 새롭고, 더 짧고 더 정확한 버전을 제공했습니다. 프리케 정식의 다각형은 다음과 같은 속성을 가집니다:
- 프리케 다각형의 꼭짓점은 모두 Γ의 궤도에 놓이는 4g 꼭짓점을 가집니다. 꼭짓점에 의한 것은 두 변이 만나는 점을 의미합니다.
- 변은 하나의 변을 쌍을 이룬 변으로 방향을 반전하여 전달하는 Γ의 고유한 원소가 있도록 구별되는 쌍에서 일치합니다. Γ의 동작은 방향-보존하는 것이므로, 한 변이 라고 불리면, 쌍의 다른 변은 반대 방향 로 표시될 수 있습니다.
- 표준 다각형의 가장자리는 인접한 변의 목록이 형식을 취하도록 배열될 수 있습니다. 즉, 변의 쌍이 이러한 방식으로 인터리브되도록 배열될 수 있습니다.
- 변은 측지선 호입니다.
- 프리케 다각형의 각 내부 각도는 다각형이 엄격하게 볼록하고 이러한 내부 각도의 합은 2π가 되도록 π보다 엄격하게 작습니다.
위의 구성은 다각형의 각 변이 리만 표면 H/Γ에서 닫힌 (비-자명한) 루프임을 보장하기에 충분합니다. 이를테면, 각 변은 따라서 기본 그룹(fundamental group)의 원소 가 될 수 있습니다. 특히, 기본 그룹 는 다음과 같은 정확하게 하나의 정의하는 제약 조건을 갖는 2g 생성기 를 가집니다:
- .
리만 표면 H/Γ의 지너스는 g입니다.
Area
표준 기본 다각형의 넓이는 이며, 여기서 g는 리만 표면의 지너스(genus)입니다 (동일하게, 여기서 4g는 다각형의 변의 개수입니다). 표준 다각형은 H/Γ의 표현이므로, 리만 표면의 전체 넓이는 표준 다각형의 넓이와 같습니다. 넓이 공식은 가우스–보네 정리(Gauss–Bonnet theorem) 를 따르고 어떤 의미에서는 리만-후르비츠 공식(Riemann–Hurwitz formula)을 통해 일반화됩니다.
Explicit form for standard polygons
회전 대칭을 갖는 정규 표준 4g-변 다각형에 대해 명시적인 표현이 제공될 수 있습니다. 이 경우에서, g-겹 회전 대칭을 갖는 지너스 g 리만 표면의 그룹은 생성기 로 주어질 수 있습니다. 이들 생성기는 위쪽 절반 평면 위에 동작하는 에 대해 다음 분수 선형 변환(fractional linear transforms)으로 제공됩니다:
매개변수는 다음에 의해 주어집니다:
그리고
그리고
이들 생성기가 다음 제약 조건을 준수하는지 확인할 수 있습니다:
이는 그룹 표시(group presentation)의 전체성을 제공합니다.
See also
Notes
- ^ See:
- ^ See:
- ^ Example of sphere construction from fundamental polygon.
- ^ E. Fedorov (1891) "Симметрія на плоскости" (Simmetriya na ploskosti, Symmetry in the plane), Записки Императорского С.-Петербургского минералогического общества (Zapiski Imperatorskova Sankt-Petersburgskova Mineralogicheskova Obshchestva, Proceedings of the Imperial St. Petersburg Mineralogical Society), 2nd series, 28 : 345–390 (in Russian).
- ^ See:
- ^ Voronoi's proof has the advantage of generalising to n dimensions: it shows that if translates of a centrally symmetric convex polyhedron tessallate Rn, then the polyhedron has at most 2(2n − 1) faces.
- ^ See:
- ^ See:
- Cassels 1997
- Kolmogorov & Yukshkevich 2001, pp. 157–159
- ^ a b c Beardon 1984
- ^ Imayoshi & Taniguchi 1992
- ^ Note that a simple polygon in the plane with n ≥ 4 vertices is homeomorphic to one, and hence any, convex n-gon by a piecewise linear homeomorphism, linear on the edges: this follows by induction on n from the observation of Max Dehn that any simple polygon possesses a diagonal, i.e. an interior chord between vertices, so can be broken up into smaller polygons; see Guggenheimer (1977). For a regular 4g-gon, the pairing between sides can be made linear, by reparametrising triangles made up of the centre and one side from each pair of sides.
- ^ Jost 2002, pp. 47–57
- ^ Shastri 2011
- ^ Farb & Margalit 2012
- ^ a b Ahlfors 2006, pp. 67–68
- ^ Farb & Margalit 2012, pp. 230–236
References
- Ahlfors, Lars V. (2006), Lectures on quasiconformal mappings, University Lecture Series, vol. 38 (Second ed.), American Mathematical Society, ISBN 978-0-8218-3644-6
- Appell, P.; Goursat, E.; Fatou, P. (1930), Théorie des fonctions algébriques d'une variable, Tome II, Fonctions automorphes, Gauthier-Vi]lars, pp. 102–154
- Bambah, R. P.; Davenport, H. (1952), "The covering of n-dimensional space by spheres", J. London Math. Soc., 27 (2): 224–229, doi:10.1112/jlms/s1-27.2.224
- Beardon, Alan F. (1983), The Geometry of Discrete Groups, Springer-Verlag, ISBN 978-0-387-90788-8
- Beardon, Alan F. (1984), A primer on Riemann surfaces, London Mathematical Society Lecture Note Series, vol. 78, Cambridge University Press, ISBN 978-0-521-27104-2
- Bonk, Marius; Schramm, Oded (2000), "Embeddings of Gromov hyperbolic spaces", Geom. Funct. Anal., 10 (2): 266–306, CiteSeerX 10.1.1.47.7874, doi:10.1007/s000390050009
- Böröczky, Károly, Jr. (2004), Finite packing and covering, Cambridge Tracts in Mathematics, vol. 154, Cambridge University Press, ISBN 978-0-521-80157-7
{{citation}}: CS1 maint: multiple names: authors list (link) - Bourdon, Marc; Pajot, Hervé (2002), "Quasiconformal geometry and hyperbolic geometry", in Marc Burger; Alessandra Iozzi (eds.), Rigidity in dynamics and geometry, Springer, pp. 1–17, ISBN 978-3-540-43243-2
- Buser, Peter (1992), Geometry and spectra of compact Riemann surfaces, Progress in Mathematics, vol. 106, Birkhäuser, doi:10.1007/978-0-8176-4992-0, ISBN 978-0-8176-3406-3
- Cassels, J. W. S. (1997), "IX. Packings", An introduction to the geometry of numbers, Classics in Mathematics, Springer-Verlag, ISBN 978-3-540-61788-4
- Coxeter, H. S. M (1962), "The Classification of Zonohedra by Means of Projective Diagrams", J. Math. Pures Appl., 41: 137–156
- Coxeter, H. S. M.; Moser, W. O. J. (1980), Generators and relations for discrete groups, vol. 14 (Fourth edition. Ergebnisse der Mathematik und ihrer Grenzgebiete ed.), Springer-Verlag, ISBN 978-3-540-09212-4
- Eggleston, H. G. (1958), Convexity, Cambridge Tracts in Mathematics and Mathematical Physics, vol. Cambridge University Press
- Farb, Benson; Margalit, Dan (2012), A primer on mapping class groups, Princeton Mathematical Series, vol. 49, Princeton University Press, ISBN 978-0-691-14794-9
- Farkas, Hershel M.; Kra, Irwin (1980), Riemann Surfaces, Springer-Verlag, ISBN 978-0-387-90465-8
- Fenchel, Werner; Nielsen, Jakob (2003), Discontinuous groups of isometries in the hyperbolic plane, de Gruyter Studies in Mathematics, vol. 29, Walter de Gruyter, ISBN 978-3-11-017526-4
- Fricke, Robert; Klein, Felix (1897), Vorlesungen über die Theorie der automorphen Funktionen, Band 1: Die gruppentheoretischen Grundlagen, Teubner, pp. 236–237, 295–320
- Grünbaum, Branko; Shephard, G. C. (1987), Tilings and patterns, W. H. Freeman, ISBN 978-0-7167-1193-3
- Guggenheimer, H. (1977), "The Jordan curve theorem and an unpublished manuscript by Max Dehn" (PDF), Archive for History of Exact Sciences, 17 (2): 193–200, CiteSeerX 10.1.1.374.1893, doi:10.1007/BF02464980, JSTOR 41133486, MR 0532231
- Hirsch, Morris W. (1994), Differential topology, Graduate Texts in Mathematics, vol. 33, Springer-Verlag, ISBN 978-0-387-90148-0
- Imayoshi, Y.; Taniguchi, M. (1992), An Introduction to Teichmüller spaces, Springer-Verlag, ISBN 978-0-387-70088-5
- Iversen, Birger (1992), Hyperbolic geometry, London Mathematical Society Student Texts, vol. 25, Cambridge University Press, ISBN 978-0-521-43508-6
- Jost, Jurgen (2002), Compact Riemann Surfaces (2nd ed.), Springer-Verlag, ISBN 978-3-540-43299-9
- Kapovich, Ilya; Benakli, Nadia (2002), "Boundaries of hyperbolic groups", Combinatorial and geometric group theory, Contemp. Math., vol. 296, American Mathematical Society, pp. 39–93
- Keen, Linda (1965), "Canonical polygons for finitely generated Fuchsian groups", Acta Math., 115: 1–16, doi:10.1007/bf02392200
- Keen, Linda (1966), "Intrinsic moduli on Riemann surfaces", Ann. of Math., 84 (3): 404–420, doi:10.2307/1970454, JSTOR 1970454
- Kolmogorov, A. N.; Yukshkevich, A. P., eds. (2001), Mathematics of the 19th Century: Mathematical Logic, Algebra, Number Theory, Probability Theory, Springer, ISBN 978-3764364410
- Lehto, Olli (1987), Univalent functions and Teichmüller spaces, Graduate Texts in Mathematics, vol. 109, Springer-Verlag, ISBN 978-0-387-96310-5
- Lyusternik, L. A. (1966), Convex figures and polyhedra, translated by Donald L. Barnett, Boston: D. C. Heath and Co.
- Nevanlinna, Rolf (1953), Uniformisierung, Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete (in German), vol. 64, Springer-Verlag
- Seifert, Herbert; Threlfall, William (1934), A textbook of topology, Pure and Applied Mathematics, vol. 89, translated by Michael A. Goldman, Academic Press, ISBN 978-0-12-634850-7
- Shastri, Anant R. (2011), Elements of differential topology, CRC Press, ISBN 978-1-4398-3160-1
- Siegel, C. L. (1971), Topics in complex function theory, Vol. II. Automorphic functions and abelian integrals, translated by A. Shenitzer; M. Tretkoff, Wiley-Interscience
- Stillwell, John (1992), Geometry of surfaces, Universitext, Springer-Verlag, ISBN 978-0-387-97743-0
- Zong, Chuanming (2014), "Packing, covering and tiling in two-dimensional spaces", Expositiones Mathematicae, 32 (4): 297–364, doi:10.1016/j.exmath.2013.12.002









































