Horner's method

Original article: wikipedia:Horner's method

수학(mathematics)과 컴퓨터 과학(computer science)에서, 호너의 방법(Horner's method) (또는 호너의 스킴(Horner's scheme))은 다항식 평가(polynomial evaluation)를 위한 알고리듬입니다. 비록 윌리엄 조지 호너(William George Horner)의 이름을 따서 지어졌지만, 이 방법은 훨씬 더 오래된 것인데, 왜냐하면 그것은 호너 자신에 의해 조제프-루이 라그랑주(Joseph-Louis Lagrange)로 귀속되었고, 수백 년 전 중국과 페르시아 수학자로 거슬러 올라갈 수 있습니다. 컴퓨터가 도입된 후, 이 알고리듬은 다항식을 효율적으로 계산하는 데 기본이 되었습니다.

그 알고리듬은 호너의 규칙(Horner's rule)을 기반으로 합니다:

${\begin{aligned}a_{0}&+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}\\&=a_{0}+x{\bigg (}a_{1}+x{\Big (}a_{2}+x{\big (}a_{3}+\cdots +x(a_{n-1}+x\,a_{n})\cdots {\big )}{\Big )}{\bigg )}.\end{aligned}}$

이것은 단지 $n$개의 곱셈과 $n$개의 덧셈으로 차수 n의 다항식(polynomial)의 평가를 허용합니다. 이것이 최적인데, 왜냐하면 더 적은 숫자의 산술 연산으로 평가될 수 없는 차수 n의 다항식이 있기 때문입니다.

대안적으로, 호너의 방법은 1819년 호너에 의해 설명된 다항식의 근을 근사하는 방법도 참조합니다. 호너의 규칙을 적용에 의해 손 계산에 더 효율적으로 만든 뉴턴-랍선법(Newton-Raphson method)의 변형입니다. 그것은 1970년경 컴퓨터가 일반화될 때까지 널리 사용되었습니다.

Polynomial evaluation and long division

다음 다항식이 주어지면

$p(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n},$

여기서 $a_{0},\ldots ,a_{n}$는 상수 계수이며, 그 문제는 $x$의 특정 값 $x_{0}$에서 다항식을 평가하는 것입니다.

이를 위해, 새로운 상수 수열은 다음과 같이 재귀적(recursively )으로 정의됩니다:

${\begin{aligned}b_{n}&:=a_{n}\\b_{n-1}&:=a_{n-1}+b_{n}x_{0}\\(1)\quad \quad \quad &~~~\vdots \\b_{1}&:=a_{1}+b_{2}x_{0}\\b_{0}&:=a_{0}+b_{1}x_{0}.\end{aligned}}$

그런-다음 $b_{0}$는 $p(x_{0})$의 값입니다.

이것이 작동하는 이유를 확인하기 위해, 다항식은 다음 형식으로 작성할 수 있습니다:

$p(x)=a_{0}+x{\bigg (}a_{1}+x{\Big (}a_{2}+x{\big (}a_{3}+\cdots +x(a_{n-1}+x\,a_{n})\cdots {\big )}{\Big )}{\bigg )}\ .$

따라서, $b_{i}$를 표현식에 반복적으로 대입함으로써,

${\begin{aligned}p(x_{0})&=a_{0}+x_{0}{\Big (}a_{1}+x_{0}{\big (}a_{2}+\cdots +x_{0}(a_{n-1}+b_{n}x_{0})\cdots {\big )}{\Big )}\\&=a_{0}+x_{0}{\Big (}a_{1}+x_{0}{\big (}a_{2}+\cdots +x_{0}b_{n-1}{\big )}{\Big )}\\&~~\vdots \\&=a_{0}+x_{0}b_{1}\\&=b_{0}.\end{aligned}}$

이제, 다음임을 증명될 수 있습니다;

$(2)\quad \quad \quad p(x)=(b_{1}+b_{2}x+b_{3}x^{2}+b_{4}x^{3}+\cdots +b_{n-1}x^{n-2}+b_{n}x^{n-1})(x-x_{0})+b_{0}$

이 표현은 다음의 결과를 결정하는 매우 빠른 방법을 제공하기 때문에 호너의 실제 적용을 구성합니다;

$p(x)/(x-x_{0})$

여기서 b₀ (p(x₀)와 같음)는 나눗셈의 나머지이며, 아래 예에서 볼 수 있습니다. 만약 x₀가 p(x)의 근이면 b₀ = 0 (나머지는 0임을 의미)이며, 이는 p(x)를 (x-x₀)으로 인수화할 수 있음을 의미합니다.

연속적인 b-값을 찾는 것과 관련하여, b_n을 결정하는 것으로 시작하며, 이는 단순히 a_n과 같습니다. 그런-다음 공식을 사용하여 b₀에 도달할 때까지 다른 b로 아래로 이동합니다;

$b_{n-1}=a_{n-1}+b_{n}x_{0}.$

Examples

$x=3$에 대해, $f(x)=2x^{3}-6x^{2}+2x-1$를 평가합니다.

우리는 다음과 같이 조립 제법(synthetic division)을 사용합니다:

 x0│   x3    x2    x1    x0
 3 │   2    −6     2    −1
   │         6     0     6
   └────────────────────────
       2     0     2     5

숫자로 이루어진 세 번째 행에서 항목은 위의 두 행에서 항목의 합입니다. 두 번째 행에서 각 항목은 x-값 (이 예에서는 3)과 바로 왼쪽에 있는 세 번째 행 항목의 곱입니다. 첫 번째 행에서 항목은 평가될 다항식의 계수입니다. 그런-다음 $x-3$으로 나눌 때 $f(x)$의 나머지는 5입니다.

그러나 다항식 나머지 정리(polynomial remainder theorem)에 의해, 우리는 나머지는 $f(3)$임을 압니다. 따라서 $f(3)=5$입니다.

이 예제에서, 만약 $a_{3}=2,a_{2}=-6,a_{1}=2,a_{0}=-1$이면 세 번째 행에서 항목 $b_{3}=2,b_{2}=0,b_{1}=2,b_{0}=5$임을 볼 수 있습니다. 따라서, 조립 제법은 호너의 방법을 기반으로 합니다.

다항식 나머지 정리의 결과로, 세 번째 행에서 항목은 $x-3$으로 나눈 $f(x)$의 몫, 이-차 다항식의 계수입니다. 나머지는 5입니다. 이것은 호너의 방법을 다항식 긴 나눗셈(polynomial long division)에 유용하게 만듭니다.

$x^{3}-6x^{2}+11x-6$을 $x-2$로 나눕니다:

 2 │   1    −6    11    −6
   │         2    −8     6
   └────────────────────────
       1    −4     3     0

몫은 $x^{2}-4x+3$입니다.

$f_{1}(x)=4x^{4}-6x^{3}+3x-5$와 $f_{2}(x)=2x-1$라고 놓습니다. $f_{1}(x)$을 호너의 방법을 사용하여 $f_{2}\,(x)$로 나눕니다:

  0.5 │ 4  -6   0   3  -5
      │     2  -2  -1   1
└───────────────────────
        4  -2  -1   1  -4

세 번째 행은 처음 두 행의 합을 2로 나눈 값입니다. 두 번째 행에서 각 항목은 1과 왼쪽의 세 번째 행 항목을 곱한 것입니다. 그 정답은

${\frac {f_{1}(x)}{f_{2}(x)}}=2x^{3}-2x^{2}-x+1-{\frac {4}{2x-1}}.$

Efficiency

차수-n 다항식의 단항식 형식을 사용한 평가는 거듭제곱이 반복된 곱셈으로 계산되고 각 단항식을 개별적으로 평가되면 많아야 n개의 덧셈과 (n² + n)/2개의 곱셈을 요구합니다. (이것은 x의 거듭제곱을 반복적으로 평가함으로써 n개의 덧셈과 2n − 1 곱셈으로 줄일 수 있습니다.) 만약 숫자 데이터가 자릿수 (또는 비트)의 관점에서 표현되면, 소박한 알고리듬은 역시 대략적으로 x의 비트 수의 2n배를 저장해야 합니다 (평가된 다항식은 근사적으로 크기 xⁿ을 가지고, xⁿ 자체도 저장해야 합니다). 대조적으로, 호너의 방법은 n개의 덧셈과 n개의 곱셈만 요구하고, 그것의 저장 요구 사항은 x의 비트 수의 오직 n배입니다. 대안적으로, 호너의 방법은 n개의 융합된 곱셈-덧셈(fused multiply–adds)으로 계산될 수 있습니다. 호너의 방법은 kn 덧셈과 곱셈을 갖는 다항식의 첫 번째 k 도함수를 평가하도록 확장될 수도 있습니다.

호너의 방법은 임의적인 다항식을 평가하는 임의의 알고리듬이 최소한으로 많은 연산을 사용해야 한다는 점에서 최적입니다. 알렉산더 오스트로우스키(Alexander Ostrowski)는 1954년에 필요한 덧셈의 수가 최소라는 것을 입증했습니다. Victor Pan은 1966년에 곱셈의 수가 최소임을 입증했습니다. 어쨌든, x가 행렬일 때, 호너의 방법은 최적이 아닙니다.

이것은 다항식이 단항식 형식에서 평가되고 표현의 사전-조건화(preconditioning)가 허용되지 않는다고 가정하며, 이는 다항식이 한 번만 평가되면 의미가 있습니다. 어쨌든, 사전-조건화가 허용되고 다항식이 여러 번 평가되면, 더 빠른 알고리듬이 가능합니다. 그것들은 다항식 표현의 변환을 포함합니다. 일반적으로, 차수-n 다항식은 ⌊n/2⌋+2 곱셈과 n 덧셈만 사용하여 평가될 수 있습니다.

Parallel evaluation

See also: Estrin's scheme

호너의 규칙의 단점은 모든 연산이 순차적으로 종속(sequentially dependent)되어 있으므로, 최신 컴퓨터에서 명령 수준 병렬 처리(instruction level parallelism)를 활용할 수 없다는 것입니다. 다항식 평가의 효율성이 중요한 대부분의 응용에서, 많은 저-차수 다항식이 (컴퓨터 그래픽에서 각 픽셀이나 다각형에 대해, 또는 수치 모의실험에서 각 격자 정사각형에 대해) 동시에 평가되므로, 단일 다항식 평가 내에서 병렬성을 찾을 필요는 없습니다.

어쨌든, 매우 높은 차수의 단일 다항식을 평가하면, 다음과 같이 분해하는 것이 유용할 수 있습니다:

${\begin{aligned}p(x)&=\sum _{i=0}^{n}a_{i}x^{i}\\&=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}\\&=\left(a_{0}+a_{2}x^{2}+a_{4}x^{4}+\cdots \right)+\left(a_{1}x+a_{3}x^{3}+a_{5}x^{5}+\cdots \right)\\&=\left(a_{0}+a_{2}x^{2}+a_{4}x^{4}+\cdots \right)+x\left(a_{1}+a_{3}x^{2}+a_{5}x^{4}+\cdots \right)\\&=\sum _{i=0}^{\lfloor n/2\rfloor }a_{2i}x^{2i}+x\sum _{i=0}^{\lfloor n/2\rfloor }a_{2i+1}x^{2i}\\&=p_{0}(x^{2})+xp_{1}(x^{2}).\\\end{aligned}}$

더 일반적으로, 합계는 k 부분으로 분리될 수 있습니다:

${\begin{aligned}p(x)&=\sum _{i=0}^{n}a_{i}x^{i}\\&=\sum _{j=0}^{k-1}x^{j}\sum _{i=0}^{\lfloor n/k\rfloor }a_{ki+j}x^{ki}\\&=\sum _{j=0}^{k-1}x^{j}p_{j}(x^{k})\\\end{aligned}}$

여기서 내부 합계는 호너 방법의 개별 병렬 인스턴스를 사용하여 평가될 수 있습니다. 이것은 기본 호너의 방법보다 약간 더 많은 연산을 요구하지만, 그것들 대부분의 k-방법 SIMD 실행을 허용합니다. 최신 컴파일러는 일반적으로 유리할 때 다항식을 이런 방법으로 평가하지만, 부동-점(floating-point) 계산에 대해 이것은 (안전하지 않은) 재결합 수학을 활성화해야 합니다.

Application to floating-point multiplication and division

Main article: multiplication algorithm § Shift and add

호너의 방법은 하드웨어 곱셈기(hardware multiplier)를 가지지 않는 마이크로컨트롤러에서 이진수의 곱셈과 나눗셈을 위한 빠르고, 코드-효율적 방법입니다. 곱할 이진수 중 하나는 자명한 다항식으로 표시되며, 여기서 (위 표기법 사용하여) $a_{i}=1$과 $x=2$입니다. 그런-다음 x (또는 x의 일부 거듭제곱)가 반복적으로 인수로 묶입니다. 이 이진 숫자-표시 시스템 (밑수 2)에서, $x=2$이므로, 2의 거듭제곱이 반복적으로 인수로 묶입니다.

Example

예를 들어, 두 숫자 (0.15625)와 m의 곱을 찾기 위해:

${\begin{aligned}(0.15625)m&=(0.00101_{b})m=(2^{-3}+2^{-5})m=(2^{-3})m+(2^{-5})m\\&=2^{-3}(m+(2^{-2})m)=2^{-3}(m+2^{-2}(m)).\end{aligned}}$

Method

두 이진 숫자 d와 m의 곱을 찾기 위해:

1. 중간 결과를 보유하는 레지스터는 d로 초기화됩니다.

2. m에서 최하위 유효숫자 (가장 오른쪽) 비-영 비트로 시작합니다.

2b. (왼쪽으로) 비-영 비트를 다음 최상위 유효 비트까지의 비트 위치 수를 셉니다. 만약 더 많은 유효 비트가 없으면, 현재 비트 위치의 값을 취합니다.

2c. 해당 값을 사용하여, 중간 결과를 보유하는 레지스터의 해당 비트 수만큼 왼쪽-시프트 연산을 수행합니다.

3. 만약 모든 비-영 비트가 세어지면, 중간 결과 레지스터는 이제 최종 결과를 보유합니다. 그렇지 않으면, 중간 결과에 d를 더하고 m에서 다음 최상위 유효 비트로 2단계를 계속합니다.

Derivation

일반적으로, 비트 값 ($d_{3}d_{2}d_{1}d_{0}$)을 갖는 이진수에 대해 그 곱은 다음입니다:

$(d_{3}2^{3}+d_{2}2^{2}+d_{1}2^{1}+d_{0}2^{0})m=d_{3}2^{3}m+d_{2}2^{2}m+d_{1}2^{1}m+d_{0}2^{0}m.$

알고리듬의 이 단계에서, 일과 같은 이진 계수만 세도록 영-값 계수를 갖는 항은 버리는 것을 요구하고, 따라서 영에 의한 곱셈 또는 영에 의한 나눗셈(division by zero)의 문제는 문제가 되지 않습니다. 인수화된 방정식에서 이 함축에도 불구하고:

$=d_{0}\left(m+2{\frac {d_{1}}{d_{0}}}\left(m+2{\frac {d_{2}}{d_{1}}}\left(m+2{\frac {d_{3}}{d_{2}}}(m)\right)\right)\right).$

분모는 모두 일과 같으므로 (또는 항이 없음), 이것은 다음과 같이 줄어듭니다:

$=d_{0}(m+2{d_{1}}(m+2{d_{2}}(m+2{d_{3}}(m)))),$

또는 동등하게 (위에서 설명된 "방법"과 일치)

$=d_{3}(m+2^{-1}{d_{2}}(m+2^{-1}{d_{1}}(m+{d_{0}}(m)))).$

이진법 (밑수-2) 수학에서, 2의 거듭제곱에 의한 곱셈은 단순히 레지스터 시프트 연산입니다. 따라서, 2를 곱하면 밑수-2에서 산술 시프트(arithmetic shift)로 계산됩니다. 인수 (2⁻¹)는 오른쪽 산술 시프트이고, a (0)는 연산을 수행하지 않으고 (2⁰ = 1은 곱셈 항등 원소이기 때문에), a (2¹)는 왼쪽 산술 시프트를 발생시킵니다. 곱셈 곱은 이제 산술 시프트 연산, 덧셈과 뺄셈만 사용하여 빠르게 계산될 수 있습니다.

이 방법은 단일 명령어 시프트-와-덧셈-누산을 지원하는 프로세서에서 특히 빠릅니다. C 부동-점 라이브러리와 비교될 때, 호너의 방법은 정확도가 약간 떨어지며, 어쨌든 명목상 13배 더 빠르고 ("정식의 부호화된 자릿수" (CSD) 형식이 사용될 때 16배 빠름) 코드 공간의 20%만 사용합니다.

Other applications

호너의 방법은 다른 위치 숫자-표시 시스템(numeral systems) 사이를 변환하기 위해 사용될 수 있고 – 이 경우에서 x는 숫자 시스템의 밑수이고, a_i 계수는 주어진 숫자의 밑수-x로 표현된 자릿수입니다 – x가 행렬이면 역시 사용될 수 있으며, 이 경우에서 계산 효율성의 이득은 훨씬 더 큽니다. 어쨌든, 그러한 경우에 대해 더 빠른 방법이 알려져 있습니다.

Polynomial root finding

긴 나누기 알고리듬을 뉴턴의 방법(Newton's method)과 함께 사용하면, 다항식의 실수 근을 근사하는 것이 가능합니다. 그 알고리듬은 다음과 같이 작동합니다. 영들 $z_{n}<z_{n-1}<\cdots <z_{1}$을 갖는 차수 $n$의 다항식 $p_{n}(x)$이 주어지면, $z_{1}<x_{0}$을 만족하는 어떤 초기 추측 $x_{0}$를 만듭니다. 이제 다음 두 단계를 반복합니다:

1. 뉴턴의 방법(Newton's method)을 사용하여, 추측 $x_{0}$를 사용하여 $p_{n}(x)$의 가장 큰 영 $z_{1}$을 찾습니다.
2. 호너의 방법을 사용하여, $(x-z_{1})$으로 나누어 $p_{n-1}$을 얻습니다. 1단계로 돌아가지만 다항식 $p_{n-1}$과 초기 추측값 $z_{1}$을 사용합니다.

이들 두 단계는 다항식에 대해 모든 실수 영들을 찾을 때까지 반복됩니다. 근사된 영들이 충분하게 정확하지 않으면, 얻은 값은 뉴턴의 방법에 대한 초기 추측으로 사용할 수 있지만 축소된 다항식이 아닌 전체 다항식을 사용할 수 있습니다.

Example

Polynomial root finding using Horner's method

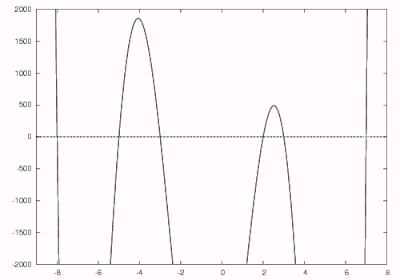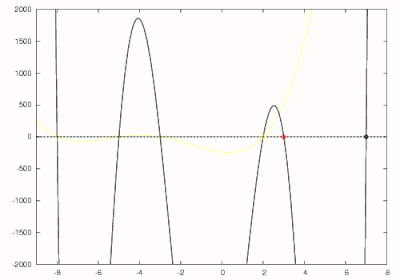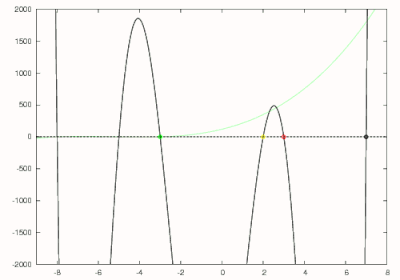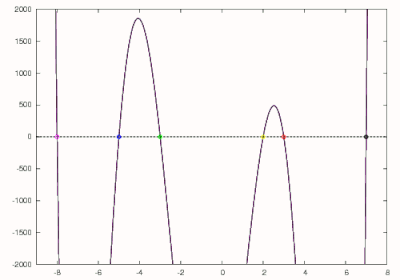
다음 다항식을 생각해 보십시오:

$p_{6}(x)=(x+8)(x+5)(x+3)(x-2)(x-3)(x-7)$

이것은 다음으로 전개될 수 있습니다:

$p_{6}(x)=x^{6}+4x^{5}-72x^{4}-214x^{3}+1127x^{2}+1602x-5040.$

위에서 우리는 이 다항식의 가장 큰 근이 7이라는 것을 알고 있으므로 초기에 8을 추측할 수 있습니다. 뉴턴의 방법을 사용하면 그림에서 검은색으로 표시된 것처럼 7의 첫 번째 영이 발견됩니다. 다음 $p(x)$를 $(x-7)$로 나누어 다음을 얻습니다:

$p_{5}(x)=x^{5}+11x^{4}+5x^{3}-179x^{2}-126x+720$

이것은 그림에서 빨간색으로 그린 것입니다. 뉴턴의 방법은 7의 초기 추측값을 갖는 이 다항식의 가장 큰 영점을 찾기 위해 사용됩니다. 원래 다항식의 두 번째로 큰 영점에 해당하는 이 다항식의 가장 큰 영점은 3에서 발견되고 빨간색 원으로 표시됩니다. 차수 5 다항식은 이제 $(x-3)$으로 나누어 다음을 얻습니다:

$p_{4}(x)=x^{4}+14x^{3}+47x^{2}-38x-240$

이것은 노란색으로 표시됩니다. 이 다항식의 영점은 뉴턴의 방법을 사용하여 다시 2에서 발견되고 노란색 원으로 표시됩니다. 호너의 방법은 이제 다음을 얻기 위해 사용됩니다:

$p_{3}(x)=x^{3}+16x^{2}+79x+120$

이는 녹색으로 표시되고 −3에서 영점을 갖는 것으로 나타났습니다. 이 다항식은 다음으로 더 축소됩니다:

$p_{2}(x)=x^{2}+13x+40$

이는 파란색으로 표시되고 −5의 영점을 산출합니다. 원래 다항식의 최종 근은 뉴턴의 방법에 대한 초기 추측값으로 최종 영을 사용하거나 $p_{2}(x)$를 줄이고 선형 방정식(linear equation)을 풀어서 찾을 수 있습니다. 보시다시피, −8, −5, −3, 2, 3, 및 7의 예상된 근이 발견되었습니다.

Divided difference of a polynomial

호너의 방법은 나누어진 차이 $(p(y)-p(x))/(y-x)$를 계산하도록 수정될 수 있습니다. (이전과 같이) 다음 다항식이 주어지면

$p(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n},$

다음처럼 진행합니다:

${\begin{aligned}b_{n}&=a_{n},&\quad d_{n}&=b_{n},\\b_{n-1}&=a_{n-1}+b_{n}x,&\quad d_{n-1}&=b_{n-1}+d_{n}y,\\&{}\ \ \vdots &\quad &{}\ \ \vdots \\b_{1}&=a_{1}+b_{2}x,&\quad d_{1}&=b_{1}+d_{2}y,\\b_{0}&=a_{0}+b_{1}x.\end{aligned}}$

완료 시, 다음을 가집니다:

${\begin{aligned}p(x)&=b_{0},\\{\frac {p(y)-p(x)}{y-x}}&=d_{1},\\p(y)&=b_{0}+(y-x)d_{1}.\end{aligned}}$

나누어진 차이의 이러한 계산은 특히 $x\approx y$일 때 $p(x)$와 $p(y)$를 개별적으로 평가하는 것보다 반올림 오류가 적습니다. 이 방법에서 $y=x$를 대입하면 $p(x)$의 도함수인 $d_{1}=p'(x)$를 제공합니다.

History

Qin Jiushao's algorithm for solving the quadratic polynomial equation$-x^{4}+763200x^{2}-40642560000=0$
result: x=840

호너의 논문은, "A new method of solving numerical equations of all orders, by continuous approximation"의 제목을 갖고 있으며, 1819년 7월 1일 런던 왕립 학회에서 1823년 속편 회의에서 낭독되었습니다. 1819년 호너의 논문 2 부 Philosophical Transactions of the Royal Society of London는 1820년 4월, The Monthly Review: or, Literary Journal의 문제에서 검토자에 의해 열렬히 환영받습니다; 이에 비해, Charles Babbage의 기술 논문은 이 검토에서 단호하게 기각되었습니다. 1821년 9월, The Monthly Review의 일련의 검토는 홀드레드(Holdred)가 수치 방정식의 직접적이고 일반적인 실용적인 해결책을 발견한 최초의 사람이라고 결론지었습니다. Fuller는 호너의 1819년 논문에 있는 방법이 나중에 "호너의 방법"으로 알려지게 된 방법과 다르며 결과적으로 이 방법의 우선 순위는 Holdred(1820)로 가야 함을 보여주었습니다.

동시대 영국인과 달리, 호너는 유럽 문학, 특히 Arbogast의 연구를 사용했습니다. 호너는 Paolo Ruffini의 연구를 무시했지만 John Bonneycastle의 대수학 책을 자세히 읽은 것으로도 알려져 있습니다.

비록 호너가 이 방법을 접근 가능하고 실용적으로 만든 것으로 알려져 있지만 호너보다 오래 전에 알려져 있었습니다. 시간 역순으로 호너의 방법은 이미 다음으로 알려져 있습니다:

• Paolo Ruffini in 1809 (루피니의 규칙(Ruffini's rule)을 참조)
• Isaac Newton in 1669
• the Chinese mathematician Zhu Shijie in the 14th century
• the Chinese mathematician Qin Jiushao in his Mathematical Treatise in Nine Sections in the 13th century
• the Persian mathematician Sharaf al-Dīn al-Ṭūsī in the 12th century (the first to use that method in a general case of cubic equation)
• the Chinese mathematician Jia Xian in the 11th century (Song dynasty)
• The Nine Chapters on the Mathematical Art, a Chinese work of the Han dynasty (202 BC – 220 AD) edited by Liu Hui (fl. 3rd century).

진 규소(Qin Jiushao)는 그의 Shu Shu Jiu Zhang (구장산술; 1247)에서 11세기 송 왕조 수학자 고 헌(Jia Xian)의 초기 연구를 기반으로 한 다항 방정식을 풀기 위한 호너-유형의 방법 포트폴리오를 제시합니다; 예를 들어, 한 가지 방법은 중국 사례 연구의 당시 관습에 따라 진이 사례를 제공하는 복-오차에 특히 적합합니다. Development of Mathematics in China and Japan (Leipzig 1913)에서 Yoshio Mikami는 다음과 같이 썼습니다:

"... 호너의 저명한 과정이 유럽에서보다 적어도 거의 6세기 전에 중국에서 사용되었다는 사실을 부정할 수 있는 사람은 ... 물론 우리는 호너의 발명을 중국 기원으로 돌리려는 의도는 전혀 없지만, 시간의 경과로 인해 유럽인이 직접 또는 간접적으로 중국 방법을 알 수 있었던 것이 완전히 불가능한 것은 아닙니다."

Ulrich Libbrecht는 다음과 같이 결론지었습니다: 이 절차는 중국 발명품임이 분명합니다 ... 그 방법은 인도에서 알려지지 않았습니다. 그는 피보나치가 아마도 중국인에게서 빌린 아랍인에게서 배웠을 것이라고 말했습니다. 유사한 견해에 따라 제곱근과 세제곱근을 추출하는 것은 Jiu Zhang Suan Shu에서 문제 IV.16과 22와 관련하여 유 휘(Liu Hui)에 의해 이미 논의되었고, 반면에 7세기 Wang Xiaotong은 그의 책 Jigu Suanjing에 설명된 근사법으로 독자들이 삼차 방정식을 풀 수 있다고 가정했습니다.

See also

• Clenshaw algorithm to evaluate polynomials in Chebyshev form
• De Boor's algorithm to evaluate splines in B-spline form
• De Casteljau's algorithm to evaluate polynomials in Bézier form
• Estrin's scheme to facilitate parallelization on modern computer architectures
• Lill's method to approximate roots graphically
• Ruffini's rule and synthetic division to divide a polynomial by a binomial of the form x − r

References

• Berggren, J. L. (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat". Journal of the American Oriental Society. 110 (2): 304–309. doi:10.2307/604533. JSTOR 604533.
• Cajori, Florian (1911). "Horner's method of approximation anticipated by Ruffini". Bulletin of the American Mathematical Society. 17 (8): 409–414. doi:10.1090/s0002-9904-1911-02072-9. Read before the Southwestern Section of the American Mathematical Society on November 26, 1910.
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein10.1016/0315-0860(81)90069-0, Clifford (2009). "Introduction to Algorithms". Historia Mathematica. 8 (3) (3rd ed.). MIT Press: 277–318. doi:10.1016/0315-0860(81)90069-0.{{cite journal}}: CS1 maint: numeric names: authors list (link)
• Fateman, R. J.; Kahan, W. (2000). Improving exact integrals from symbolic algebra systems (PDF) (Report). PAM. University of California, Berkeley: Center for Pure and Applied Mathematics. Archived from the original (PDF) on 2017-08-14. Retrieved 2018-05-17.
• Fuller, A. T. (1999). "Horner versus Holdred: An Episode in the History of Root Computation". Historia Mathematica. 26: 29–51. doi:10.1006/hmat.1998.2214.
• Higham, Nicholas (2002). Accuracy and Stability of Numerical Algorithms. SIAM. ISBN 978-0-89871-521-7.
• Holdred, T. (1820). A New Method of Solving Equations with Ease and Expedition; by which the True Value of the Unknown Quantity is Found Without Previous Reduction. With a Supplement, Containing Two Other Methods of Solving Equations, Derived from the Same Principle (PDF). Richard Watts. Archived from the original (PDF) on 2014-01-06. Retrieved 2012-12-10.

  Holdred's method is in the supplement following page numbered 45 (which is the 52nd page of the pdf version).

• Horner, William George (July 1819). "A new method of solving numerical equations of all orders, by continuous approximation". Philosophical Transactions. 109. Royal Society of London: 308–335. doi:10.1098/rstl.1819.0023. JSTOR 107508. S2CID 186210512.

  Directly available online via the link, but also reprinted with appraisal in D.E. Smith: A Source Book in Mathematics, McGraw-Hill, 1929; Dover reprint, 2 vols, 1959.

• Knuth, Donald (1997). The Art of Computer Programming. Vol. 2: Seminumerical Algorithms (3rd ed.). Addison-Wesley. pp. 486–488 in section 4.6.4. ISBN 978-0-201-89684-8.
• Kress, Rainer (1991). Numerical Analysis. Springer.
• Kripasagar, Venkat (March 2008). "Efficient Micro Mathematics – Multiplication and Division Techniques for MCUs". Circuit Cellar Magazine (212).
• Libbrecht, Ulrich (2005). "Chapter 13". Chinese Mathematics in the Thirteenth Century (2nd ed.). Dover. ISBN 978-0-486-44619-6. Archived from the original on 2017-06-06. Retrieved 2016-08-23.
• Mikami, Yoshio (1913). "Chapter 11. Ch'in Chiu-Shao". The Development of Mathematics in China and Japan (1st ed.). Chelsea Publishing Co reprint. pp. 74–77.
• Ostrowski, Alexander M. (1954). "On two problems in abstract algebra connected with Horner's rule". Studies in Mathematics and Mechanics presented to Richard von Mises. Academic Press. pp. 40–48. ISBN 978-1-4832-3272-0.
• Pan, Y. Ja (1966). "On means of calculating values of polynomials". Russian Math. Surveys. 21: 105–136. doi:10.1070/rm1966v021n01abeh004147. S2CID 250869179.
• Pankiewicz, W. (1968). "Algorithm 337: calculation of a polynomial and its derivative values by Horner scheme". Communications of the ACM. 11 (9). ACM: 633. doi:10.1145/364063.364089. S2CID 52859619.
• Spiegel, Murray R. (1956). Schaum's Outline of Theory and Problems of College Algebra. McGraw-Hill.
• Temple, Robert (1986). The Genius of China: 3,000 Years of Science, Discovery, and Invention. Simon and Schuster. ISBN 978-0-671-62028-8.
• Whittaker, E.T.; Robinson, G. (1924). The Calculus of Observations. London: Blackie.
• Wylie, Alexander (1897). "Jottings on the Science of Chinese Arithmetic". Chinese Researches. Shanghai. pp. 159–194.{{cite book}}: CS1 maint: location missing publisher (link)

  Reprinted from issues of The North China Herald (1852).

External links

• "Horner scheme", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Qiu Jin-Shao, Shu Shu Jiu Zhang (Cong Shu Ji Cheng ed.)
• For more on the root-finding application see [1]