Mean

Original article: w:Mean

This article is about the mathematical concept. For other uses, see Mean (disambiguation).

For the state of being mean or cruel, see Meanness.

For broader coverage of this topic, see Average.

수학(mathematics), 특히 통계(statistics)에서, 평균(mean)은 여러 종류가 있습니다.

데이터 집합(data set)에 대해, 산술 평균(arithmetic mean 또는 (arithmetic average)은 유한 숫자 집합의 중심 값입니다: 구체적으로 특별히, 값의 합을 값의 개수로 나눈 값입니다. 숫자 집합 x₁, x₂, ..., x_n의 산술 평균은 전형적으로 ${\bar {x}}$로 표시됩니다. 만약 데이터 집합이 통계적 모집단(statistical population)에서 표본화(sampling)에 의해 얻어진 일련의 관찰을 기반으로 하면, 산술 평균은 표본 평균(sample mean) (${\bar {x}}$로 표시)에서 기본 분포의 평균, 또는 기댓값(expected value), 모집단 평균(population mean) ($\mu$ 또는 $\mu _{x}$)을 구별하기 위한 것입니다.

확률과 통계 외에도, 다양한 다른 평균의 개념이 기하학(geometry)과 수학적 해석학(mathematical analysis)에서 자주 사용됩니다; 예제는 아래에 나와 있습니다.

Types of means

Pythagorean means

Main article: Pythagorean means

Arithmetic mean (AM)

Main article: Arithmetic mean

숫자 목록의 산술 평균(또는 단순히 평균)은 모든 숫자의 합을 숫자의 개수로 나눈 것입니다. 비슷하게, 표본 $x_{1},x_{2},\ldots ,x_{n}$의 평균은, 보통 ${\bar {x}}$로 표시되며, 표본에서 표본화된 값의 합계를 표본의 항목의 개수로 나눈 값입니다:

${\bar {x}}={\frac {1}{n}}\left(\sum _{i=1}^{n}{x_{i}}\right)={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}$

예를 들어, 4, 36, 45, 50, 75의 다섯 값의 산술 평균은 다음과 같습니다:

${\frac {4+36+45+50+75}{5}}={\frac {210}{5}}=42.$

Geometric mean (GM)

Main article: geometric mean

기하 평균(geometric mean)은 양수 집합에 유용한 평균으로, 그 합 (산술 평균의 경우)이 아니라 곱 (성장률의 경우)에 따라 해석됩니다:

${\bar {x}}=\left(\prod _{i=1}^{n}{x_{i}}\right)^{\frac {1}{n}}=\left(x_{1}x_{2}\cdots x_{n}\right)^{\frac {1}{n}}$

예를 들어, 4, 36, 45, 50, 75의 다섯 값의 기하 평균은 다음과 같습니다:

$(4\times 36\times 45\times 50\times 75)^{\frac {1}{5}}={\sqrt[{5}]{24\;300\;000}}=30.$

Harmonic mean (HM)

조화 평균(harmonic mean)은 속력(speed) (즉, 단위 시간당 거리)의 경우와 같이 일부 단위(unit)와 관련하여 정의된 숫자의 집합에 유용한 평균입니다:

${\bar {x}}=n\left(\sum _{i=1}^{n}{\frac {1}{x_{i}}}\right)^{-1}$

예를 들어, 4, 36, 45, 50, 75의 다섯 값의 조화 평균은 다음과 같습니다:

${\frac {5}{{\tfrac {1}{4}}+{\tfrac {1}{36}}+{\tfrac {1}{45}}+{\tfrac {1}{50}}+{\tfrac {1}{75}}}}={\frac {5}{\;{\tfrac {1}{3}}\;}}=15.$

Relationship between AM, GM, and HM

Proof without words of the inequality of arithmetic and geometric means:
PR is a diameter of a circle centred on O; its radius AO is the arithmetic mean of a and b. Using the geometric mean theorem, triangle PGR's altitude GQ is the geometric mean. For any ratio a:b, AO ≥ GQ.

Main article: Inequality of arithmetic and geometric means

AM, GM, 및 HM는 이들 부등식을 만족시킵니다:

$\mathrm {AM} \geq \mathrm {GM} \geq \mathrm {HM} \,$

주어진 표본의 모든 원소가 같으면 등호가 유지됩니다.

Statistical location

See also: Average § Statistical location

it is Comparison of the arithmetic mean, median and mode of two skewed (log-normal) distributions.

Geometric visualization of the mode, median and mean of an arbitrary probability density function.

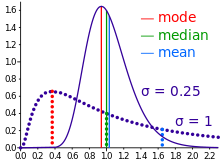
기술 통계학(descriptive statistics)에서, 평균은 중앙값(median), 최빈값(mode), 또는 중간-범위(mid-range)와 혼동될 수 있는데, 왜냐하면 이들 중 하나가 "평균" (보다 공식적으로, 중심 경향(central tendency)의 측정)이라고 불릴 수 있기 때문입니다. 관찰의 집합의 평균은 값의 산술 평균입니다; 어쨌든, 기울어진 분포(skewed distributions)에 대해, 평균은 반드시 중간 값 (중앙값), 또는 가장 가능성이 높은 값 (최빈값)과 같지 않습니다. 예를 들어, 평균 소득은 전형적으로 매우 큰 소득을 가진 소수의 사람들에 의해 위쪽으로 치우치므로, 대다수가 평균보다 소득이 낮습니다. 대조적으로, 중앙 소득 (중위 소득)은 인구의 절반이 아래에 있고 절반이 위에 있는 수준입니다. 최빈 소득은 가장 가능성이 높은 소득이고 소득이 낮은 많은 사람들을 포함합니다. 중앙값과 최빈값은 종종 그러한 기울어진 데이터에 대한 보다 직관적인 측정이지만, 많은 기울어진 분포는 지수(exponential)와 푸아송(Poisson) 분포를 포함하여 실제로 그들 평균에 의해 가장 잘 설명됩니다.

Mean of a probability distribution

Main article: Expected value

See also: Population mean

확률 분포(probability distribution)의 평균은 해당 분포를 갖는 랜덤 변수(random variable)의 장기적인 산술 평균입니다. 만약 확률 변수가 $X$로 표시되면, 그것은 역시 $X$의 기댓값(expected value) ($E(X)$로 표시됨)으로 알려져 있습니다. 이산 확률 분포(discrete probability distribution)에 대해, 평균은 $\textstyle \sum xP(x)$로 주어지며, 여기서 합은 확률 변수의 모든 가능한 값에 취해지고 $P(x)$는 확률 질량 함수(probability mass function)입니다. 연속 분포(continuous distribution)에 대해, 평균은 $\textstyle \int _{-\infty }^{\infty }xf(x)\,dx$이고, 여기서 $f(x)$는 확률 밀도 함수(probability density function)입니다. 분포가 이산도 아니고 연속도 아닌 것들을 포함하여 모든 경우에서, 평균은 확률 측정(probability measure)에 관한 확률 변수의 르베그 적분(Lebesgue integral)입니다. 평균이 존재하거나 유한할 필요는 없습니다; 일부 확률 분포에 대해 평균이 무한대 (+∞ 또는 −∞)이지만, 다른 분포에 대해 평균은 정의되지 않습니다.

Generalized means

Power mean

일반화된 평균(generalized mean)은, 역시 거듭제곱 평균 또는 횔더 평균으로 알려져 있으며, 이차, 산술, 기하, 및 조화 평균의 추상화입니다. 그것은 n 개의 양수 x_i의 집합에 대해 다음과 같이 정의됩니다:

${\bar {x}}(m)=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{m}\right)^{\frac {1}{m}}$

매개변수 m에 대해 다른 값을 선택함으로써, 다음 평균의 유형이 얻습니다:

$m\rightarrow \infty$	$x_{i}$의 최댓값(maximum)
$m=2$	이차 평균(quadratic mean)
$m=1$	산술 평균(arithmetic mean)
$m\rightarrow 0$	기하 평균(geometric mean)
$m=-1$	조화 평균(harmonic mean)
$m\rightarrow -\infty$	$x_{i}$의 최솟값(minimum)

f-mean

이것은 일반화된 f-평균(generalized f-mean)으로 더 일반화될 수 있습니다:

${\bar {x}}=f^{-1}\left({{\frac {1}{n}}\sum _{i=1}^{n}{f\left(x_{i}\right)}}\right)$

그리고 다시 역-가능한 f의 적절한 선택은 다음을 제공할 것입니다:

$f(x)=x$	산술 평균(arithmetic mean),
$f(x)={\frac {1}{x}}$	조화 평균(harmonic mean),
$f(x)=x^{m}$	거듭제곱 평균(power mean),
$f(x)=\ln(x)$	기하 평균(geometric mean).

Weighted arithmetic mean

가중된 산술 평균(weighted arithmetic mean) (또는 가중된 평균)은 같은 모집단의 다른 크기 샘플에서 평균 값을 결합하기를 원하면 사용됩니다:

${\bar {x}}={\frac {\sum _{i=1}^{n}{w_{i}{\bar {x_{i}}}}}{\sum _{i=1}^{n}w_{i}}}.$

여기서 ${\bar {x_{i}}}$와 $w_{i}$는 각각 표본 $i$의 평균과 크기입니다. 다른 응용에서, 그것들은 각 값에 의해 평균에 미치는 영향의 신뢰도에 대한 측정을 나타냅니다.

Truncated mean

때때로, 숫자의 집합은 이상값 (즉, 다른 것보다 훨씬 낮거나 훨씬 높은 데이터 값)을 포함할 수 있습니다. 종종, 이상값은 아티팩트(artifacts)로 인한 잘못된 데이터입니다. 이 경우에서, 우리는 잘린 평균(truncated mean)을 사용할 수 있습니다. 그것은 상단 또는 하단에서 데이터의 주어진 부분을 버리는 것을 포함하며, 전형적으로 각 끝에서 같은 양을 취하고 그런-다음 남아있는 데이터의 산술 평균을 취하는 것입니다. 제거된 값의 숫자는 값의 총 숫자의 백분율로 나타냅니다.

Interquartile mean

사분위수-사이 평균(Interquartile mean)은 잘린 평균의 구체적인 예입니다. 그것은 가장 낮은 값과 가장 높은 값의 4분의 1을 제거한 후의 단순히 산술 평균입니다:

${\bar {x}}={\frac {2}{n}}\;\sum _{i={\frac {n}{4}}+1}^{{\frac {3}{4}}n}\!\!x_{i}$

값이 순서화되었다고 가정하면, 특정 가중치의 집합에 대해 가중화된 평균의 특정 예제일 뿐입니다.

Mean of a function

Main article: Mean of a function

어떤 환경에서, 수학자들이 값의 무한 (또는 심지어 셀-수-없는(uncountable)) 집합의 평균을 계산할 수 있습니다. 이것은 함수 $f(x)$의 평균값 $y_{\text{avg}}$을 계산할 때 발생할 수 있습니다. 직관적으로, 함수의 평균은 곡선의 단면 아래 면적을 계산하고, 그런-다음 해당 단면의 길이로 나누는 것으로 생각될 수 있습니다. 이것은 모눈종이의 제곱수를 세어 조잡하게 수행되거나, 더 정확하게는 적분(integration)을 통해 수행될 수 있습니다. 적분 공식은 다음과 같이 작성됩니다:

$y_{\text{avg}}(a,b)={\frac {1}{b-a}}\int \limits _{a}^{b}\!f(x)\,dx$

이 경우에서, 적분이 수렴하는지 확인하기 위해 주의를 기울여야 합니다. 그러나 함수 자체가 어떤 지점에서 무한대로 가는 경향이 있더라도 평균은 유한일 수 있습니다.

Mean of angles and cyclical quantities

각도(angle), 시간, 및 기타 주기적인 양은 숫자를 더하기 위해 모듈러 산술(modular arithmetic)을 요구하고 그렇지 않으면 숫자를 결합하는 것을 요구합니다. 모든 이들 상황에서, 고유한 평균은 없을 것입니다. 예를 들어, 자정 전후의 한 시간은 자정과 정오 모두에 등거리입니다. 그것은 역시 평균이 존재하지 않을 수도 있습니다. 색상 환(color wheel)을 생각해 보십시오 – 모든 색상의 집합에 대한 평균은 없습니다. 이러한 상황에서, 어떤 평균이 가장 유용한지 결정해야 합니다. 평균화하기 전에 값을 조정하거나, 순환 수량의 평균에 대해 특수 접근 방식을 사용함으로써 이것을 수행할 수 있습니다.

Fréchet mean

프레셰 평균은 표면(surface) 또는 보다 일반적으로, 리만 매니폴드(Riemannian manifold)에서 질량 분포의 "중심"을 결정하는 방식을 제공합니다. 다른 많은 평균과 달리, 프레셰 평균은 그것들의 원소가 반드시 함께 더해지거나 스칼라로 곱해질 수 없는 공간에 정의됩니다. 그것은 때때로 Karcher 평균 (Hermann Karcher의 이름을 따서 지어짐)이라고도 합니다.

Swanson's rule

이것은 적당히 기울어진 분포에 대해 평균에 대한 근사치입니다. 그것은 탄화수소 탐사에 사용되고 다음과 같이 정의됩니다:

$m=0.3P_{10}+0.4P_{50}+0.3P_{90}$

여기서 P₁₀, P₅₀, 및 P₉₀는 분포의 10번째, 50번째, 및 90번째 백분위수입니다.

Other means

Main category: Means

• Arithmetic-geometric mean
• Arithmetic-harmonic mean
• Cesàro mean
• Chisini mean
• Contraharmonic mean
• Elementary symmetric mean
• Geometric-harmonic mean
• Grand mean
• Heinz mean
• Heronian mean
• Identric mean
• Lehmer mean
• Logarithmic mean
• Moving average
• Neuman–Sándor mean
• Quasi-arithmetic mean
• Root mean square (quadratic mean)
• Rényi's entropy (a generalized f-mean)
• Spherical mean
• Stolarsky mean
• Weighted geometric mean
• Weighted harmonic mean

See also

• Central tendency
  • Median
  • Mode
• Descriptive statistics
• Kurtosis
• Law of averages
• Mean value theorem
• Moment (mathematics)
• Summary statistics
• Taylor's law