Parity of a permutation

Original article: w:Parity of a permutation

Permutations of 4 elements

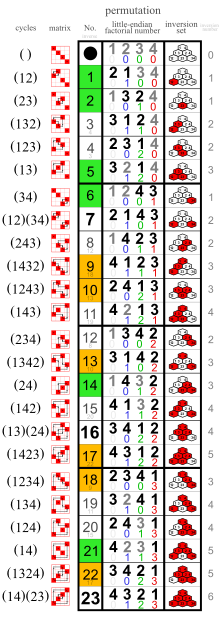
Odd permutations have a green or orange background. The numbers in the right column are the inversion numbers (OEIS에서 수열 A034968), which have the same parity as the permutation.

수학(mathematics)에서, X가 적어도 두 개의 원소를 갖는 유한 집합일 때, X의 순열 (즉, X에서 X로의 전단사 함수)은 같은 크기의 두 가지 클래스: 짝수 순열(even permutations)과 홀수 순열(odd permutations)로 나뉩니다. 만약 X의 임의의 전체 순서화(total ordering)가 고정되면, X의 순열 $\sigma$의 패리티 (홀수성 또는 짝수성)는 $\sigma$에 대한 반전(inversions)의 개수의 패리티, 즉 x < y와 σ(x) > σ(y)를 만족하는 X의 원소 x, y의 쌍의 패리티로 정의될 수 있습니다.

순열 $\sigma$의 부호(sign, signature, 또는 signum)는 sgn(σ)로 표시되고 σ가 짝수이면 +1로 정의되고 σ가 홀수이면 −1로 정의됩니다. 시그니처는 대칭 그룹(symmetric group) S_n의 교대하는 캐릭터(character)를 정의합니다. 순열의 부호에 대한 또 다른 표기법은 보다 일반적인 레비-치비타 기호(Levi-Civita symbol) (ε_σ)로 제공되며, 이는 X에서 X로의 모든 맵에 대해 정의되고, 비-전전사 맵(non-bijective maps)에 대해 값 영을 가집니다.

순열의 부호는 다음과 같이 명시적으로 표현될 수 있습니다:

sgn(σ) = (−1)^N(σ)

여기서 N(σ)는 σ에서 반전(inversions)의 개수입니다.

대안적으로 순열 σ의 부호는 전치(transpositions)의 곱으로의 분해에서 다음과 같이 정의될 수 있습니다:

sgn(σ) = (−1)^m

여기서 m은 분해에서 전치의 개수입니다. 비록 그러한 분해가 고유하지는 않을지라도, 모든 분해에서 전치의 개수의 패리티는 동일하며, 순열의 부호가 잘-정의되어 있음을 의미합니다.

Example

$\sigma (1)=3,$ $\sigma (2)=4,$ $\sigma (3)=5,$ $\sigma (4)=2,$ 및 $\sigma (5)=1$로 정의된 집합 {1, 2, 3, 4, 5}의 순열 σ를 생각해 보십시오. 한-줄 표기법에서, 이 순열은 34521로 표시됩니다. 그것은 세 가지 전치에 의해 항등 순열(identity permutation) 12345에서 얻을 수 있습니다: 먼저 숫자 2와 4를 교환하고, 그런-다음 3과 5를 교환하고, 마지막으로 1과 3을 교환합니다. 이것은 주어진 순열 σ는 홀수임을 보여줍니다. 순환 표기법(cycle notation) 기사의 방법에 따라, 이것은 오른쪽에서 왼쪽으로 구성하여 다음과 같이 쓸 수 있습니다:

$\sigma ={\begin{pmatrix}1&2&3&4&5\\3&4&5&2&1\end{pmatrix}}={\begin{pmatrix}1&3&5\end{pmatrix}}{\begin{pmatrix}2&4\end{pmatrix}}={\begin{pmatrix}1&3\end{pmatrix}}{\begin{pmatrix}3&5\end{pmatrix}}{\begin{pmatrix}2&4\end{pmatrix}}.$

예를 들어 σ를 전치의 합성(compositio)으로 쓰는 많은 다른 방법이 있습니다:

σ = (1 5)(3 4)(2 4)(1 2)(2 3),

그러나 짝수 전치의 결과로 쓰는 것은 불가능합니다.

Properties

항등 순열은 짝수 순열입니다. 짝수 순열은 짝수의 합성과 두 원소의 짝수 교환 (전치라고 불림)만으로 구성되어 얻을 수 있고, 반면에 홀수 순열은 홀수 전치만으로 얻을 수 있습니다.

다음 규칙은 정수의 덧셈에 대한 해당 규칙을 직접 따릅니다:

• 두 개의 짝수 순열의 합성은 짝수입니다.
• 두 개의 홀수 순열의 합성은 짝수입니다.
• 홀수 순열과 짝수 순열의 합성은 홀수입니다.

이것으로부터 다음임이 따라옵니다:

• 모든 짝수 순열의 역수는 짝수입니다.
• 모든 홀수 순열의 역수는 홀수입니다.

집합 {1, ..., n}의 모든 순열의 대칭 그룹(symmetric group) S_n을 고려하여, 모든 각 순열에 그 시그니처를 할당하는 다음과 같은 맵이

sgn: S_n → {−1, 1} 

그룹 준동형(group homomorphism)이라고 결론내릴 수 있습니다.

게다가, 짝수 순열이 S_n의 부분그룹(subgroup)을 형성한다는 것을 알 수 있습니다. 이것은 A_n으로 표시되는 n 문자의 교대하는 그룹입니다. 그것은 준동형 sgn의 커널(kernel)입니다. 두 개의 홀수 순열의 합성은 짝수이기 때문에 홀수 순열은 부분그룹을 형성할 수 없지만, 그것들은 (S_n에서) A_n의 코셋(coset)을 형성합니다.

만약 n > 1이면, S_n에는 홀수 순열이 있는 만큼 많은 짝수 순열이 있습니다; 결과적으로, A_n은 n!/2개의 순열을 포함합니다. (그 이유는 σ가 짝수이면 (1  2)σ는 홀수이고, σ가 홀수이면 (1  2)σ는 짝수이고, 이들 두 맵은 서로 역이기 때문입니다.)

순환(cycle)이 짝수인 것과 그 길이가 홀수인 것은 필요충분 조건입니다. 이것은 다음과 같은 공식에서 따릅니다:

$(a\ b\ c\ d\ e)=(d\ e)(c\ e)(b\ e)(a\ e){\text{ or }}(a\ b)(b\ c)(c\ d)(d\ e).$

실제로, 주어진 순열이 짝수인지 홀수인지 결정하기 위해, 순열을 서로소 순환의 곱으로 씁니다. 그 순열이 홀수인 것과 이 인수분해가 홀수 개의 짝수-길이 순환을 포함하는 것은 필요충분 조건입니다.

주어진 순열이 짝수인지 홀수인지 결정하는 또 다른 방법은 해당 순열 행렬(permutation matrix)을 구성하고 행렬식을 계산하는 것입니다. 행렬식의 값은 순열의 패리티와 같습니다.

홀수 차수(order)의 모든 각 순열은 짝수여야 합니다. A₄에서 순열 (1 2)(3 4)은 그 전환은 일반적으로 참이 아님을 보여줍니다.

Equivalence of the two definitions

이 섹션은 순열 σ의 패리티가 두 가지 동등한 방법으로 정의될 수 있다는 증명을 제시합니다:

• (임의의 순서화 아래에서) σ에서 반전의 개수의 패리티; 또는
• σ가 분해될 수 있는 전치의 개수의 패리티 (어쨌든 우리는 그것을 분해하기 위해 선택했습니다).

Proof 1

σ를 랭크된 도메인 S 위에 순열이라고 놓습니다. 모든 각 순열은 전치 (2-원소 교환)의 순열에 의해 생성될 수 있습니다. 다음을 그러한 분해 중 하나라고 놓습니다:

σ = T₁ T₂ ... T_k

우리는 k의 패리티가 σ의 반전의 개수의 패리티와 같다는 것을 보여주기를 원합니다.

모든 각 전치는 인접한 원소, 예를 들어 다음과 같이 홀수 전치의 곱으로 쓸 수 있습니다:

(2 5) = (2 3) (3 4) (4 5) (4 3) (3 2).

일반적으로, 집합 {1,...,i,...,i+d,...} 위에 전치 (i i+d)를 d에 대한 재귀에 의한 2d−1 인접 전치의 합성으로 쓸 수 있습니다:

• 기본 경우 d=1는 자명합니다.

• 재귀 경우에서, 먼저 (i, i+d)를 (i, i+1) (i+1, i+d) (i, i+1)라고 다시 씁니다. 그런-다음 재귀적으로 (i+1, i+d)를 인접 전치로 다시 씁니다.

만약 위의 각 전치 T₁ ... T_k를 이러한 방법으로 분해하면, 우리는 새로운 분해를 얻습니다:

σ = A₁ A₂ ... A_m

여기서 모든 A₁...A_m는 인접한 것입니다. 역시, m의 패리티는 k의 패리티와 같습니다.

이것은 사실입니다: 모든 순열 τ와 인접 전치 a에 대해, aτ는 τ보다 하나 적거나 하나 더 많은 반전을 가집니다. 다시 말해서, 인접 전치로 합성될 때 순열의 반전의 개수의 패리티가 전환됩니다.

그러므로, σ의 반전의 개수의 패리티는 정확히 m의 패리티이며, 이는 역시 k의 패리티입니다. 이것이 우리가 증명하기로 설정한 것입니다.

따라서 우리는 σ의 패리티를 임의의 분해에서 구성 전치의 개수로 정의할 수 있습니다. 그리고 이것은 위에서 볼 수 있듯이 임의의 순서화 아래에서 반전의 개수의 패리티와 일치해야 합니다. 그러므로, 정의는 실제로 잘 정의되어 있고 동등합니다.

Proof 2

대안적인 증명은 방데르몽드 다항식을 사용합니다:

$P(x_{1},\ldots ,x_{n})=\prod _{i<j}(x_{i}-x_{j}).$

따라서 예를 들어 n = 3 경우에서, 우리는 다음을 가집니다:

$P(x_{1},x_{2},x_{3})=(x_{1}-x_{2})(x_{2}-x_{3})(x_{1}-x_{3}).$

이제 숫자 {1, ..., n}의 주어진 순열 σ에 대해, 우리는 다음을 정의합니다:

$\operatorname {sgn} (\sigma )={\frac {P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}{P(x_{1},\ldots ,x_{n})}}.$

다항식 $P(x_{\sigma (1)},\dots ,x_{\sigma (n)})$은 그것들의 부호를 제외하고 $P(x_{1},\dots ,x_{n})$와 같은 인수를 가지기 때문에, sgn(σ)가 +1 또는 −1임이 따라옵니다. 게다가, 만약 σ 및 τ가 두 순열이면, 다음임을 알 수 있습니다:

${\begin{aligned}\operatorname {sgn} (\sigma \tau )&={\frac {P(x_{\sigma (\tau (1))},\ldots ,x_{\sigma (\tau (n))})}{P(x_{1},\ldots ,x_{n})}}\\[4pt]&={\frac {P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}{P(x_{1},\ldots ,x_{n})}}\cdot {\frac {P(x_{\sigma (\tau (1))},\ldots ,x_{\sigma (\tau (n))})}{P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}}\\[4pt]&=\operatorname {sgn} (\sigma )\cdot \operatorname {sgn} (\tau ).\end{aligned}}$

이 정의와 함께 두 원소의 임의의 전치가 시그니처 −1을 가진다는 것이 더욱 분명해지기 때문에, 우리는 실제로 앞에서 정의한 대로 시그니처를 복구합니다.

Proof 3

세 번째 접근 방식은 생성기 τ₁, ..., τ_n−1와 다음 관계의 관점에서 그룹 S_n의 표현을 사용합니다:

• $\tau _{i}^{2}=1$  for all i
• $\tau _{i}^{}\tau _{i+1}\tau _{i}=\tau _{i+1}\tau _{i}\tau _{i+1}$   for all i < n − 1
• $\tau _{i}^{}\tau _{j}=\tau _{j}\tau _{i}$   if $|i-j|\geq 2.$

[여기서 생성기 $\tau _{i}$는 전치 (i, i + 1)를 나타냅니다.] 모든 관계는 단어의 길이를 같게 유지하거나 2씩 변경합니다. 따라서 짝수-길이의 단어로 시작하는 것은 관계식을 사용한 후에는 항상 짝수-길이의 단어를 초래하고, 홀수-길이의 단어도 마찬가지입니다. 따라서 S_n의 원소를 짝수-길이의 단어로 표현하면 "even", 홀수-길이의 단어로 표현하면 "odd"라고 부르는 것이 명확합니다.

Proof 4

x < y이고 σ(x) > σ(y)임을 만족하는 x, y 쌍은 반전이라고 불리는 것을 상기하십시오. 우리는 반전의 개수가 2-원소 교환의 개수와 같은 패리티를 가짐을 보여주기를 원합니다. 이를 위해, 우리는 어떤 두 원소가 교체되고 어떤 순열이 이미 적용되었는지에 관계없이 모든 각 교체가 반전의 개수의 패리티를 변경한다는 것을 보여줄 수 있습니다. 우리가 i번째 원소와 j번째 원소를 교환하고 싶다고 가정해 보겠습니다. 분명히, [i, j] 외부의 원소와 i 또는 j에 의해 형성된 반전은 영향을 받지 않을 것입니다. 구간 (i, j) 내의 n = j − i − 1 원소에 대해, 그들 중 v_i가 i와 반전을 형성하고 그들 중 v_j가 j와 반전을 형성한다고 가정합니다. 만약 i와 j가 바뀌면, i와의 v_i 반전은 사라지지만, n − v_i 반전이 형성됩니다. 따라서 얻은 반전 i의 개수는 n − 2v_i이며, 이는 n과 같은 패리티를 가집니다.

마찬가지로, 얻은 반전 j의 개수도 n과 같은 패리티를 가집니다. 그러므로, 조합된 둘에 의해 얻은 반전의 개수는 2n 또는 0과 같은 패리티를 가집니다. 이제 우리가 i번째 원소와 j번째 원소를 교환함으로써 얻은 (또는 손실된) 반전을 세면, 우리는 이 교환이 반전의 개수의 패리티를 변경하는 것을 볼 수 있는데, 왜냐하면 우리는 역시 (i,j) 쌍에 대해 얻은 (또는 손실된) 반전의 개수에 1을 더하기 (또는 빼기) 때문입니다.

처음에 스왑이 적용되지 않을 때, 반전의 개수는 0임에 주목하십시오. 이제 우리는 순열의 패리티에 대한 두 가지 정의의 동등성을 얻습니다.

Proof 5

전치의 두 원소에 의해 압착되는 원소를 생각해 보십시오. 각각은 두 전치 원소의 완전히 위에, 완전히 아래에, 또는 사이에 위치합니다.

완전히 위에 있거나 완전히 아래에 있는 원소는 전치가 적용될 때 반전의 개수에 아무런 영향을 주지 않습니다. 그 사이의 원소는 $2$에 기여합니다.

전치 자체는 $\pm 1$ 반전을 제공하고, 모든 다른 것은 0 (mod 2) 반전을 제공하기 때문에, 전치로 인해 반전의 개수의 패리티가 변경됩니다.

Other definitions and proofs

$n$ 점들의 순열의 패리티도 그것의 순환 구조(cycle structure)로 인코딩됩니다.

σ = (i₁ i₂ ... i_r+1)(j₁ j₂ ... j_s+1)...(ℓ₁ ℓ₂ ... ℓ_u+1)를 σ를 서로서 순환으로 고유한 분해라고 놓으며, 이는 그것들이 교환하기 때문에 임의의 순서로 합성될 수 있습니다. k + 1개 점을 포함하는 순환 (a b c ... x y z)은 항상 k 전치 (2-순환)를 합성함으로써 얻을 수 있습니다:

$(a\ b\ c\dots x\ y\ z)=(a\ b)(b\ c)\dots (x\ y)(y\ z),$

따라서 k를 순환의 크기라고 부르고, 이 정의 아래에서 전치의 주기는 크기 1이라는 것을 관찰하십시오. m개의 서로소 순환으로의 분해로부터, 우리는 σ를 k₁ + k₂ + ... + k_m 전치로 분해될 수 있으며, 여기서 k_i는 i번째 순환의 크기입니다. 숫자 N(σ) = k₁ + k₂ + ... + k_m는 σ의 판별식이라고 불리고, σ의 고정 점을 1-순환으로 포함하도록 주의한다면 다음과 같이 계산될 수도 있습니다:

$n{\text{ minus the number of disjoint cycles in the decomposition of }}\sigma$

순열 σ 이후에 전치 (a b)가 적용된다고 가정합니다. a와 b가 σ의 서로 다른 순환에 있을 때,

$(a\ b)(a\ c_{1}\ c_{2}\dots c_{r})(b\ d_{1}\ d_{2}\dots d_{s})=(a\ c_{1}\ c_{2}\dots c_{r}\ b\ d_{1}\ d_{2}\dots d_{s})$,

그리고 a와 b가 σ의 같은 순환에 있으면,

$(a\ b)(ac_{1}c_{2}\dots c_{r}\ b\ d_{1}\ d_{2}\dots d_{s})=(a\ c_{1}\ c_{2}\dots c_{r})(b\ d_{1}\ d_{2}\dots d_{s})$.

두 경우 모두에서, N((a b)σ) = N(σ) ± 1임을 알 수 있으므로, N((a b)σ)의 패리티는 N(σ)의 패리티와 다를 것입니다.

만약 σ = t₁t₂ ... t_r가 순열 σ를 전치로 임의적으로 분해하면, 항등식 (그것의 N이 0) 뒤에 t_r 뒤에 ... 뒤에 t₂ 뒤에 $t_{1}$을 적용함으로써 N(σ)와 r이 같은 패리티를 가짐을 관찰하십시오. σ의 패리티를 N(σ)의 패리티로 정의함으로써, 짝수 길이 분해를 가지는 순열은 짝수 순열이고 하나의 홀수 길이 분해를 가지는 순열은 홀수 순열입니다.

Remarks

• 위의 논증을 주의 깊게 살펴보면 r ≥ N(σ)임을 알 수 있고, σ를 그것의 크기 합이 r인 순환으로의 임의의 분해는 r개의 전치의 합성으로 표현될 수 있기 때문에, 숫자 N(σ)는 σ의 분해에서 순환의 크기의 가능한 최소 합이며, 모든 순환이 전치인 경우를 포함합니다.
• 이 증명은 σ가 작용하는 점들의 집합에 (아마도 임의적인) 차수를 도입하지 않습니다.

Generalizations

패리티는 콕서터 그룹(Coxeter groups)으로 일반화될 수 있습니다: (대칭 그룹, 인접 전치에 대해) 생성기의 선택에 따라 달라지는 길이 함수(length function) ℓ(v)를 정의하고, 그런-다음 함수 v ↦ (−1)^ℓ(v)는 일반화된 부호 맵을 제공합니다.

See also

• The fifteen puzzle is a classic application
• Zolotarev's lemma

References

• Weisstein, Eric W. "Even Permutation". MathWorld.
• Jacobson, Nathan (2009). Basic algebra. Vol. 1 (2nd ed.). Dover. ISBN 978-0-486-47189-1.
• Rotman, J.J. (1995). An introduction to the theory of groups. Graduate texts in mathematics. Springer-Verlag. ISBN 978-0-387-94285-8.
• Goodman, Frederick M. Algebra: Abstract and Concrete. ISBN 978-0-9799142-0-1.
• Meijer, Paul Herman Ernst; Bauer, Edmond (2004). Group theory: the application to quantum mechanics. Dover classics of science and mathematics. Dover Publications. ISBN 978-0-486-43798-9.