Cyclic permutation

수학(mathematics), 특히 그룹 이론(group theory)에서, 순환 순열(cyclic permutation, 또는 cycle)은 X의 모든 다른 원소를 고정하면서 X의 일부 부분-집합(subset) S의 원소를 순환 방식으로 서로 매핑하는 일부 집합(set) X의 원소의 순열(permutation)입니다. 만약 S가 k 원소를 가지면, 그 순환은 k-순환이라고 불립니다.

예를 들어, X = {1, 2, 3, 4}가 주어지면, 1을 3, 3을 2, 2를 4, 및 4를 1 (따라서 S = X)로 보내는 순열은 4-순환이고, 순열은 1을 3, 3을 2, 2를 1, 및 4를 4 (따라서 S = {1, 2, 3}이고 4는 고정된 원소임)로 보내는 것은 3-순환입니다. 다른 한편으로, 1을 3, 3을 1, 2를 4, 및 4를 2로 보내는 순열은 {1, 3}과 {2, 4} 쌍을 따로따로 순열시키기 때문에 순환 순열이 아닙니다.

집합 S는 순환의 궤도(orbit)라고 불립니다. 유한하게 많은 원소에 대한 모든 각 순열은 서로소 궤도에서 순환으로 분해될 수 있습니다.

순열의 순환 부분은 순환(cycles)이므로, 두 번째 예는 3-순환과 1-순환 (또는 고정된 점)로 구성되고 세 번째는 두 개의 2-순환으로 구성됩니다.

Definition

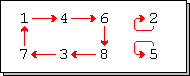
Diagram of a cyclic permutation with two fixed points; a 6-cycle and two 1-cycles.

순열(permutation)이 순환 순열이라고 불리는 것과 그것이 비-자명한 순환 (길이 > 1의 순환)를 가지는 것은 필요충분 조건입니다.^[1]

예를 들어, 두-줄(two-line), 두 가지 방법)로 쓰인 순열과 역시 순환 표기법은,

{\begin{pmatrix}1&2&3&4&5&6&7&8\\4&2&7&6&5&8&1&3\end{pmatrix}}={\begin{pmatrix}1&4&6&8&3&7&2&5\\4&6&8&3&7&1&2&5\end{pmatrix}}=(146837)(2)(5),

여섯-순환입니다; 그것의 순환 다이어그램은 오른쪽에 보입니다.

일부 저자는 정의를 하나의 비-자명한 순환으로 구성된 순열로만 제한합니다 (즉, 고정된 점이 허용되지 않습니다).^[2]

A cyclic permutation with no trivial cycles; an 8-cycle.

예를 들어, 다음 순열은

{\begin{pmatrix}1&2&3&4&5&6&7&8\\4&5&7&6&8&2&1&3\end{pmatrix}}={\begin{pmatrix}1&4&6&2&5&8&3&7\\4&6&2&5&8&3&7&1\end{pmatrix}}=(14625837)

이러한 보다 제한적인 정의 아래에서 순환 순열이지만, 앞의 예는 그렇지 않습니다.

보다 형식적으로, 전단사 함수(bijective function) $\sigma :X\to X$ 로 보이는 집합 X의 순열 $\sigma$ 는 만약 $\sigma$ 에 의해 생성된 부분그룹의 X 위에 작용이 단일 원소 이상을 갖는 많아야 하나의 궤도를 가지면 순환이라고 불립니다.^[3] 이 개념은 X가 유한 집합일 때 가장 공통적으로 사용됩니다; 그때에 물론 가장 큰 궤도 S도 유한합니다. $s_{0}$ 를 S의 임의의 원소라고 놓고, 임의의 $i\in \mathbf {Z}$ 에 대해 $s_{i}=\sigma ^{i}(s_{0})$ 를 입력합니다. 만약 S가 유한하면, $s_{k}=s_{0}$ 인 최소 숫자 $k\geq 1$ 이 있습니다. 그때에 $S=\{s_{0},s_{1},\ldots ,s_{k-1}\}$ 이고, $\sigma$ 는 다음과 $X\setminus S$ 의 임의의 원소에 대해 $\sigma (x)=x$ 에 의해 정의된 순열입니다:

\sigma (s_{i})=s_{i+1}

for 0 ≤ i < k

$\sigma$ 에 의해 고정되지 않은 원소는 다음과 같이 그릴 수 있습니다:

s_{0}\mapsto s_{1}\mapsto s_{2}\mapsto \cdots \mapsto s_{k-1}\mapsto s_{k}=s_{0}

.

순환은 간결한 순환 표기법(cycle notation) $\sigma =(s_{0}~s_{1}~\dots ~s_{k-1})$ 을 사용하여 쓸 수 있습니다 (k-튜플(tuple)과의 혼동을 피하기 위해 이 표기법에서는 원소 사이에 쉼표가 없습니다). 순환의 길이는 가장 큰 궤도의 원소 개수입니다. 길이 k의 순환은 k-순환이라고도 불립니다.

1-순환의 궤도는 순열의 고정된 점이라고 불리지만, 순열로서 모든 각 1-순환마다 항등 순열(identity permutation)입니다.^[4] 순환 표기법이 사용될 때, 혼동이 발생하지 않을 때 1-순환이 종종 억제됩니다.

Basic properties

대칭 그룹(symmetric groups)에 대한 기본 결과 중 하나는 임의의 순열이 서로소(disjoint) 순환 (보다 정확하게: 서로소 궤도를 갖는 순환)의 곱으로 표현될 수 있다고 말합니다; 그러한 순환은 서로 교환적이고, 순열의 표현은 순환의 순서까지 고유합니다.^{[Note 1]} 따라서 이 표현 (순환 유형)에서 순환의 길이의 중복집합(multiset)은 순열에 의해 고유하게 결정되고, 대칭 그룹에서 순열의 시그니처와 켤레 클래스(conjugacy class) 둘 다는 그것에 의해 결정됩니다.^[5]

대칭 그룹 S_n에서 k-순환의 숫자는, $1\leq k\leq n$ 에 대해, 다음 동등한 공식에 의해 주어집니다:

{\binom {n}{k}}(k-1)!={\frac {n(n-1)\cdots (n-k+1)}{k}}={\frac {n!}{(n-k)!k}}

k-순환은 시그니처(signature) (−1)^k − 1를 가집니다.

Transpositions

오직 둘의 원소를 갖는 순환은 전치(transposition)라고 불립니다. 예를 들어, 순열 $\pi ={\begin{pmatrix}1&2&3&4\\1&4&3&2\end{pmatrix}}$ 는 2와 4를 교환한 것입니다.

Properties

임의의 순열은 전치의 합성(composition, 곱)으로 표현될 수 있습니다—형식적으로, 그것들은 그룹(group)의 생성자(generators)입니다.^[6] 실제로, 순열되는 집합이 어떤 정수 n에 대해 {1, 2, ..., n}일 때, 임의의 순열은 인접 전치(adjacent transpositions) $(1~2)$ , $(2~3)$ , $(3~4)$ , 등의 곱으로 표현될 수 있습니다. 이는 임의적인 전치가 인접 전치들의 곱으로 표현될 수 있기 때문임을 따릅니다. 구체적으로, $k<l$ 에서 $k$ 를 $l$ 로 한 번에 한 단계씩 이동하고, 그런-다음 $l$ 을 $k$ 가 있던 위치로 다시 이동하여 $k<l$ 인 전치 $(k~~l)$ 를 표현할 수 있으며, 이들 두 가지를 서로 교환하고 다른 변경 사항은 없습니다:

(k~~l)=(k~~k+1)\cdot (k+1~~k+2)\cdots (l-1~~l)\cdot (l-2~~l-1)\cdots (k~~k+1).

순열을 전치의 곱으로 분해하는 것은 예를 들어 순열을 서로소 순환의 곱으로 쓰고, 그런-다음 길이 3 이상의 각 순환을 전치의 곱과 길이가 하나 작은 순환으로 반복적으로 분할함으로써 얻습니다:

(a~b~c~d~\ldots ~y~z)=(a~b)\cdot (b~c~d~\ldots ~y~z)

이것은 초기 요청이 $a$ 를 $b$ 로, $b$ 를 $c$ 로, $y$ 를 $z$ 로, 및 마지막으로 $z$ 를 $a$ 로 이동하는 것임을 의미합니다. 대신 오른쪽 원소를 먼저 실행함으로써 $a$ 를 유지하는 원소를 굴릴 수 있습니다 (연산자 표기법에서 평소와 같이, 순열(Permutations)에 대한 기사의 규칙을 따릅니다). 이것은 $z$ 를 $b$ 의 위치로 이동시켰으므로, 첫 번째 순열 후에, 원소 $a$ 와 $z$ 는 아직 최종 위치에 있지 않습니다. 그 후에 실행된 전치 $(a~b)$ 는 처음에 $a$ 와 $z$ 였던 것을 교환하기 위해 $b$ 의 인덱스에 의해 $z$ 를 지정합니다.

사실, 대칭 그룹(symmetric group)은 콕서터 그룹(Coxeter group)이며, 그것이 순서 2의 원소 (인접 전치)에 의해 생성되고, 모든 관계는 특정 형식의 것임을 의미합니다.

대칭 그룹에 대한 주요 결과 중 하나는 주어진 순열을 전치로의 모든 분해는 짝수 개의 전치를 갖거나, 그것들 모두는 홀수 개의 전치를 가진다는 것입니다.^[7] 이것은 순열의 패리티(parity of a permutation)를 잘-정의된(well-defined) 개념으로 허용합니다.

Notes

^ Bogart, Kenneth P. (1990), Introductory Combinatorics (2nd ed.), Harcourt, Brace, Jovanovich, p. 486, ISBN 0-15-541576-X
^ Gross, Jonathan L. (2008), Combinatorial Methods with Computer Applications, Chapman & Hall/CRC, p. 29, ISBN 978-1-58488-743-0
^ Fraleigh 1993, p. 103
^ Rotman 2006, p. 108
^ Rotman 2006, p. 117, 121
^ Rotman 2006, p. 118, Prop. 2.35
^ Rotman 2006, p. 122

^ Note that the cycle notation is not unique: each k-cycle can itself be written in k different ways, depending on the choice of $s_{0}$ in its orbit.

References

Anderson, Marlow and Feil, Todd (2005), A First Course in Abstract Algebra, Chapman & Hall/CRC; 2nd edition. ISBN 1-58488-515-7.
Fraleigh, John (1993), A first course in abstract algebra (5th ed.), Addison Wesley, ISBN 978-0-201-53467-2
Rotman, Joseph J. (2006), A First Course in Abstract Algebra with Applications (3rd ed.), Prentice-Hall, ISBN 978-0-13-186267-8
Sagan, Bruce E. (1991), The Symmetric Group / Representations, Combinatorial Algorithms & Symmetric Functions, Wadsworth & Brooks/Cole, ISBN 978-0-534-15540-7

External links

This article incorporates material from cycle on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

[1] Bogart, Kenneth P. (1990), Introductory Combinatorics (2nd ed.), Harcourt, Brace, Jovanovich, p. 486, ISBN 0-15-541576-X

[2] Gross, Jonathan L. (2008), Combinatorial Methods with Computer Applications, Chapman & Hall/CRC, p. 29, ISBN 978-1-58488-743-0

[3] Fraleigh 1993, p. 103

[4] Rotman 2006, p. 108

[6] Rotman 2006, p. 117, 121

[7] Rotman 2006, p. 118, Prop. 2.35

[8] Rotman 2006, p. 122

[5] Note that the cycle notation is not unique: each k-cycle can itself be written in k different ways, depending on the choice of $s_{0}$ in its orbit.

[1]

[2]

[3]

[4]

[Note 1]

[5]

[6]

[7]