Saddle point

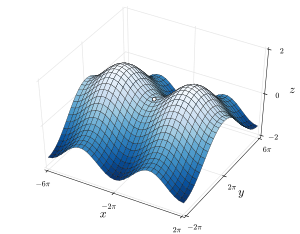
수학(mathematics)에서, 안장 점(saddle point) 또는 최소-최대 점(minimax point)은^[1] 직교 방향에서 기울기 (도함수)가 모두 영 (임계 점)이지만, 함수의 지역적 극단값(local extremum)이 아닌 함수의 그래프의 표면 위의 점입니다.^[2] 안장 점의 예제는 하나의 축 방향 (정점 사이)을 따라 상대적 최솟값(minimum)과 교차 축을 따라 상대적 최댓값(relative maximum)을 갖는 임계 점이 있을 때입니다. 어쨌든, 안장 점이 이 형식일 필요는 없습니다. 예를 들어, 함수 $f(x,y)=x^{2}+y^{3}$ 는 상대적 최댓값도 아니고 상대적 최솟값도 아니기 때문에 안장 점인 $(0,0)$ 에 임계 점을 가지지만, 그것은 $y$ -방향에서 상대적 최댓값 또는 상대적 최솟값을 가지지 않습니다.

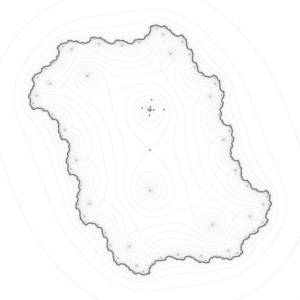
그 이름은 이 차원의 원형적 예제가 지표형식 안장(landform saddle)을 형성하는 두 봉우리 사이의 산길이나 승마용 안장과 같이 한 방향에서 위로 휘고 다른 방향에서 아래로 휘는 표면이라는 사실에서 파생됩니다. 윤곽 선(contour lines)의 관점에서, 이차원에서 안장 점은 그 점에서 교차하는 한 쌍의 선을 갖는 윤곽선 지도를 생성합니다. 그러한 교차점은 안장 점의 높이가 그러한 지도에서 사용되는 정수 배수와 일치하지 않을 가능성이 높기 때문에 실제 병기 조사 지도에서는 드뭅니다. 대신, 안장 점은 그것에 접근하고 반대 방향으로 향하는 4개의 윤곽 선의 집합 중간에 빈 공간으로 나타납니다. 기본 안장 점에 대해, 이들 집합은 직교 방향에 위치된 반대쪽 높은 쌍과 반대쪽 낮은 쌍을 갖는 쌍으로 발생합니다. 중요한 윤곽 선은 일반적으로 직각으로 교차할 필요가 없습니다.

Mathematical discussion

두 실수 변수의 실수-값 함수 F(x,y)의 주어진 정류 점이 안장 점인지 확인하는 간단한 기준은 해당 점에서 함수의 헤세 행렬(Hessian matrix)을 계산하는 것입니다: 만약 헤세가 비-한정(indefinite)이면, 해당 점은 안장 점입니다. 예를 들어, 정류 점 $(x,y,z)=(0,0,0)$ 에서 함수 $z=x^{2}-y^{2}$ 의 헤세 행렬은 다음 행렬입니다:

{\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}

이는 비-한정적입니다. 그러므로, 이 점은 안장 점입니다. 이 기준은 충분 조건만을 제공합니다. 예를 들어, 점 $(0,0,0)$ 은 $z=x^{4}-y^{4}$ 함수의 안장 점이지만, 원점에서 이 함수의 헤세 행렬은 비-한정적이지 않은 널 행렬(null matrix)입니다.

가장 일반적인 용어에서, 매끄러운 함수(smooth function, 그 그래프가 곡선, 표면, 또는 초표면임)에 대해 안장 점은 곡선/표면/등과 같은 정류 점입니다. 해당 점의 이웃(neighborhood)은 해당 점에서 접 공간(tangent space)의 어느 한 쪽에 완전히 있지 않습니다.

일차원 도메인에서, 안장 점은 정류 점(stationary point)인 동시에 변곡 점(point of inflection)이 되는 점입니다. 그것이 변곡 점이기 때문에, 그것은 지역적 극단값(local extremum)이 아닙니다.

Saddle surface

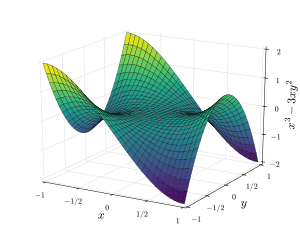
안장 표면(saddle surface)은 하나 이상의 안장 점을 포함하는 매끄러운 표면(smooth surface)입니다.

유클리드 공간에서 이-차원 안장 표면의 고전적인 예제는 이차 표면, 쌍곡선 포물면체 $z=x^{2}-y^{2}$ (종종 "그 안장 표면" 또는 "표준 안장 표면"이라고 함)와 한 판의 쌍곡면체(Hyperboloid of one sheet)입니다. 프링글스(Pringles) 감자 칩 또는 크리스프는 쌍곡선 포물면체 모양의 일상적인 예제입니다.

안장 표면은 양의 가우스 곡률(Gaussian curvature)을 가지는 볼록/타원형 표면과 구별되는 음의 가우스 곡률을 가집니다. 고전적인 삼차 안장 표면은 원숭이 안장(monkey saddle)입니다.^[3]

Examples

연속 공간 위에 정의되는 2인용 제로섬(zero sum) 게임에서 평형(equilibrium) 점은 안장 점입니다.

이-차 선형 자율 시스템에 대해, 임계 점(critical point)은 특성 방정식(characteristic equation)이 하나의 양의 고윳값과 하나의 음의 고윳값을 가지면 안장 점입니다.^[4]

상등 제약 조건에 따른 최적화에서, 일-차 조건은 라그랑주(Lagrangian)의 안장 점을 설명합니다.

Other uses

동역학적 시스템(dynamical systems)에서, 만약 동역학적이 미분-가능 맵 f에 의해 주어지면 점은 점이 쌍곡형(hyperbolic)인 것과 ƒ ⁿ의 미분 (여기서 n은 점의 주기임)이 해당 점에서 계산될 때 (복소) 단위 원 위에 고윳값을 가지지 않는 것은 필요충분 조건입니다. 그런-다음 안장 점은 그것의 안정 매니폴드(stable manifolds)와 불안정 매니폴드(unstable manifolds)가 영이 아닌 차원을 가지는 쌍곡형 주기적 점(periodic point)입니다.

행렬의 안장 점은 열에서 가장 큰 원소이자 행에서 가장 작은 원소입니다.

References

Citations

^ Howard Anton, Irl Bivens, Stephen Davis (2002): Calculus, Multivariable Version, p. 844.
^ Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (3rd ed.). New York: McGraw-Hill. p. 312. ISBN 0-07-010813-7.
^ Buck, R. Creighton (2003). Advanced Calculus (3rd ed.). Long Grove, IL: Waveland Press. p. 160. ISBN 1-57766-302-0.
^ von Petersdorff 2006

Sources

Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L.; Frank, David H.; Fristedt, Bert (1990), Calculus two: linear and nonlinear functions, Berlin: Springer-Verlag, p. 375, ISBN 0-387-97388-5
Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York, NY: Chelsea, ISBN 978-0-8284-1087-8
von Petersdorff, Tobias (2006), "Critical Points of Autonomous Systems", Differential Equations for Scientists and Engineers (Math 246 lecture notes)
Widder, D. V. (1989), Advanced calculus, New York, NY: Dover Publications, p. 128, ISBN 0-486-66103-2
Agarwal, A., Study on the Nash Equilibrium (Lecture Notes)

External links

Media related to Saddle point at Wikimedia Commons

[1] Howard Anton, Irl Bivens, Stephen Davis (2002): Calculus, Multivariable Version, p. 844.

[2] Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (3rd ed.). New York: McGraw-Hill. p. 312. ISBN 0-07-010813-7.

[3] Buck, R. Creighton (2003). Advanced Calculus (3rd ed.). Long Grove, IL: Waveland Press. p. 160. ISBN 1-57766-302-0.

[4] von Petersdorff 2006

[1]

[2]

[3]

[4]