68–95–99.7 rule

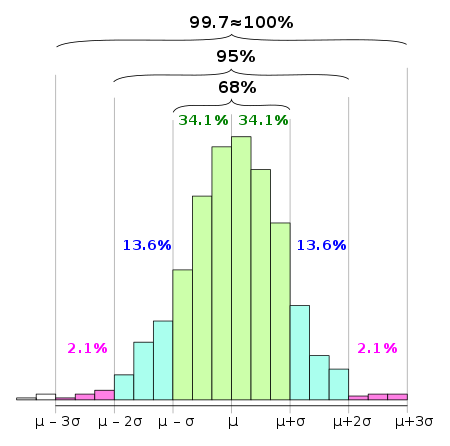
통계(statistics)에서, 68–95–99.7 규칙은, 역시 경험적 규칙(empirical rule)이라고 알려져 있으며, 정규 분포(normal distribution)에서 구간 추정(interval estimate) 내에 놓이는 값의 퍼센트: 각각 평균(mean)의 일, 이, 및 삼 표준 편차(standard deviation) 내에 놓이는 값의 68%, 95% 및 99.7%을 기억하기 위해 사용되는 약칭입니다.

수학 표기법에서, 이들 사실은 다음과 같이 표현될 수 있습니다. 여기서 $Χ$ 는 정규적으로 분포된 확률 변수(random variable)로부터 관측치, $μ$ 는 분포의 평균이고 $σ$ 는 표준 편차입니다:

{\begin{aligned}\Pr(\mu -1\sigma \leq X\leq \mu +1\sigma )&\approx 68.27\%\\\Pr(\mu -2\sigma \leq X\leq \mu +2\sigma )&\approx 95.45\%\\\Pr(\mu -3\sigma \leq X\leq \mu +3\sigma )&\approx 99.73\%\end{aligned}}

이 휴리스틱의 유용성은 특히 고려 중인 질문에 따라 다릅니다.

경험적 과학(empirical science)에서, 소위 삼-시그마 엄지손가락의 법칙(three-sigma rule of thumb)은 거의 모든 값이 평균의 삼 표준 편차 내에 놓이는 것으로 여겨지는 전통적인 휴리스틱(heuristic)을 표현하고, 따라서 99.7% 확률(probability)을 거의 확실성으로 취급하는 것이 경험적으로 유용합니다.^[1]

사회 과학(social sciences)에서, 결과의 신뢰 수준이 이-시그마 효과 (95%) 정도이면 결과가 "상당한(significant)" 것으로 여길 수 있지만, 입자 물리학(particle physics)에서, 발견(discovery)으로 인정받기 위해 요구되는 오-시그마 효과 (99.99994% 신뢰)의 관례가 있습니다.

더 약한 삼-시그마 규칙은 체비쇼프의 부등식(Chebyshev's inequality)에서 파생될 수 있고, 심지어 비-정규적으로 분포된 변수에 대해 경우의 적어도 88.8%가 적절하게 계산된 삼-3시그마 간격 내에 떨어져야 함을 말합니다. 단일-봉우리 분포(unimodal distributions)에 대해, 구간 내에 있을 확률은 비소찬스키–페투닌 부등식(Vysochanskij–Petunin inequality)에 의해 적어도 95%입니다. 이 확률이 적어도 98%가 되도록 강제하는 분포에 대한 특정 가정이 있을 수 있습니다.^[2]

Cumulative distribution function

이들 숫자 값 "68%, 95%, 99.7%"는 정규 분포의 누적 분포 함수에서 유래합니다.

임의의 표준 점수(standard score) z에 대한 예측 구간은 숫자적으로 (1−(1−Φ_μ,σ²(z))·2)에 해당합니다.

예를 들어, $Φ(2) \approx 0.9772$ , 또는 $Pr(X \leq μ + 2 σ) \approx 0.9772$ 는 (1 − (1 − 0.97725)·2) = 0.9545 = 95.45%의 예측 구간에 해당합니다. 이것은 대칭 구간이 아닙니다 – 이것은 단지 관측이 $μ + 2 σ$ 보다 작을 확률입니다. 관측이 평균의 이 표준 편차 내에 있을 확률을 계산하기 위해 (반올림으로 인한 작은 차이):

\Pr(\mu -2\sigma \leq X\leq \mu +2\sigma )=\Phi (2)-\Phi (-2)\approx 0.9772-(1-0.9772)\approx 0.9545

이것은 통계에서 사용될 때 신뢰 구간(confidence interval)과 관련이 있습니다: ${\bar {X}}\pm 2{\frac {\sigma }{\sqrt {n}}}$ 는 ${\bar {X}}$ 가 크기 $n$ 의 표본의 평균일 때 근사적으로 95% 신뢰 구간입니다.

Normality tests

"68–95–99.7 규칙"은, 모집단이 정규인 것으로 가정되면, 그것의 표준 편차가 주어지면 무언가에 대한 대략적인 확률 추정치를 빠르게 얻기 위해 자주 사용됩니다. 그것은 역시, 모집단이 정규로 가졍되면, 이상값(outliers)에 대해 단순 테스트로 사용되고, 모집단이 잠재적으로 정규가 아니면 정규성 테스트(normality test)로 사용됩니다.

표본에서 여러 표준 편차로 전달하기 위해, 우리는 먼저 모집단 평균을 알고 있는지 아니면 추정만 하는지에 따라 오차 또는 잔여(error or residual)에서 편차(deviation)를 계산합니다. 다음 단계는 모집단 매개변수를 알고 있으면 표준화(standardizing) (모집단 표준 편차로 나눔)이고, 매개변수가 알려져 있지 않고 추정만 가능하면 스튜던트화(studentizing) (표준 편차 추정치로 나눔)입니다.

이상값에 대한 테스트 또는 정규성 테스트로 사용하기 위해, 우리는 표준편차의 관점에서 편차의 크기를 계산하고, 이것을 예상 빈도와 비교합니다. 표본 집합이 주어지면, 우리는 스튜던트화 잔여(studentized residual)를 계산하고 이것들을 예상된 빈도와 비교할 수 있습니다: 노름에서 3 표준 편차 이상 떨어지는 점은 이상값일 가능성이 높고 (표본 크기(sample size)가 상당히 크지 않은 한, 어느 시점에서 우리는 표본이 극단적인 것으로 예상합니다), 만약 노름에서 3 표준 편차 이상에 많은 점이 있으면, 우리는 분포의 가정된 정규성에 의문을 제기할 이유를 가질 것입니다. 이것은 4 이상의 표준 편차의 이동에 대해 더욱 강력하게 유지됩니다.

우리는 푸아송 분포에 의해 주어진 크기 이상의 극단적인 움직임의 수를 근사화하여 더 정확하게 계산할 수 있지만, 간단히, 만약 우리가 크기 1,000의 표본에서 4개의 표준 편차 움직임을 여러 번 가지면, 우리는 이들 이상값을 고려해야 할 강력한 이유를 가지거나 분포의 가정된 정규성에 강한 의문을 제기합니다.

예를 들어, 6σ 사건은 약 10억분의 2의 확률에 해당합니다. 묘사하자면, 만약 사건이 매일 발생한다고 가정하면, 이것은 140만 년마다 예상되는 사건에 해당합니다. 이것은 간단한 정규성 테스트(simple normality test)를 제공합니다: 만약 우리가 일일 데이터에서 6σ를 목격하고 100만년보다 훨씬 적은 시간이 지나면, 정규 분포는 이 관점에서 큰 편차의 크기 또는 빈도에 대해 좋은 모델을 제공하지 않을 가능성이 큽니다.

The Black Swan에서, Nassim Nicholas Taleb는 검은 월요일(Black Monday) 폭락이 36-σ 사건에 해당하는 것을 따르는 위험 모델의 예제를 제공합니다: 그러한 사건의 발생은 즉시 모델에 결함이 있음을 시사해야 합니다. 즉, 고려 사항 아래에서 과정은 정규 분포에 의해 만족스럽게 모델링되지 않습니다. 정제된 모델은 그런-다음 예를 들어, 확률적 변동성(stochastic volatility)의 도입에 의해 고려되어야 합니다. 그러한 논의에서 도박꾼의 오류(Gambler's fallacy)의 문제를 인식하는 것이 중요하며, 이 오류는 희귀한 사건에 대한 단일 관찰이 그 사건이 실제로 드문 것과 모순되지 않는다는 것입니다. 희박하다고 알려진 사건이 여러 개 관찰되면서 발생하는 사건이 드물다는 가설, 즉 가정된 모델의 타당성이 점점 약화됩니다. 가설에서 신뢰의 점차적인 상실의 이 과정의 적절한 모델링은 가설 자체뿐만 아니라 모든 가능한 대안 가설에 이전 확률(prior probability)의 지정을 포함합니다. 이러한 이유로, 통계적 가설 테스팅(statistical hypothesis testing)은 가능성이 있다고 여겨지는 가설을 확인하는 것이 아니라 가능성이 없다고 여겨지는 가설을 반박함으로써 작동합니다.

Table of numerical values

정규 분포의 지수 꼬리 때문에, 더 높은 편차의 확률은 매우 빠르게 감소합니다. 매일 사건에 대한 정규적으로 분포된 데이터에 대한 규칙에서:

Range	Expected fraction of population inside range			Approximate frequency for daily event
μ ± 0.5σ	0.382924922548026	3 in	5	Four or five times a week
μ ± σ	0.682689492137086	1 in	3	Twice a week
μ ± 1.5σ	0.866385597462284	1 in	7	Weekly
μ ± 2σ	0.954499736103642	1 in	22	Every three weeks
μ ± 2.5σ	0.987580669348448	1 in	81	Quarterly
μ ± 3σ	0.997300203936740	1 in	370	Yearly
μ ± 3.5σ	0.999534741841929	1 in	2149	Every 6 years
μ ± 4σ	0.999936657516334	1 in	15787	Every 43 years (twice in a lifetime)
μ ± 4.5σ	0.999993204653751	1 in	147160	Every 403 years (once in the modern era)
μ ± 5σ	0.999999426696856	1 in	1744278	Every 4776 years (once in recorded history)
μ ± 5.5σ	0.999999962020875	1 in	26330254	Every 72090 years (thrice in history of modern humankind)
μ ± 6σ	0.999999998026825	1 in	506797346	Every 1.38 million years (twice in history of humankind)
μ ± 6.5σ	0.999999999919680	1 in	12450197393	Every 34 million years (twice since the extinction of dinosaurs)
μ ± 7σ	0.999999999997440	1 in	390682215445	Every 1.07 billion years (four occurrences in history of Earth)
μ ± $x$ σ	$\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)$	1 in	${\tfrac {1}{1-\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)}}$	Every ${\tfrac {1}{1-\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)}}$ days

References

^ this usage of "three-sigma rule" entered common usage in the 2000s, e.g. cited in Schaum's Outline of Business Statistics. McGraw Hill Professional. 2003. p. 359, and in Grafarend, Erik W. (2006). Linear and Nonlinear Models: Fixed Effects, Random Effects, and Mixed Models. Walter de Gruyter. p. 553.
^
See:
- Wheeler, D. J.; Chambers, D. S. (1992). Understanding Statistical Process Control. SPC Press.
- Czitrom, Veronica; Spagon, Patrick D. (1997). Statistical Case Studies for Industrial Process Improvement. SIAM. p. 342.
- Pukelsheim, F. (1994). "The Three Sigma Rule". American Statistician. 48: 88–91. JSTOR 2684253.

External links

"The Normal Distribution" by Balasubramanian Narasimhan
"Calculate percentage proportion within x sigmas at WolframAlpha

[1] this usage of "three-sigma rule" entered common usage in the 2000s, e.g. cited in Schaum's Outline of Business Statistics. McGraw Hill Professional. 2003. p. 359, and in Grafarend, Erik W. (2006). Linear and Nonlinear Models: Fixed Effects, Random Effects, and Mixed Models. Walter de Gruyter. p. 553.

[2] See:
Wheeler, D. J.; Chambers, D. S. (1992). Understanding Statistical Process Control. SPC Press.

Czitrom, Veronica; Spagon, Patrick D. (1997). Statistical Case Studies for Industrial Process Improvement. SIAM. p. 342.

Pukelsheim, F. (1994). "The Three Sigma Rule". American Statistician. 48: 88–91. JSTOR 2684253.

[3] Wheeler, D. J.; Chambers, D. S. (1992). Understanding Statistical Process Control. SPC Press.

[4] Czitrom, Veronica; Spagon, Patrick D. (1997). Statistical Case Studies for Industrial Process Improvement. SIAM. p. 342.

[5] Pukelsheim, F. (1994). "The Three Sigma Rule". American Statistician. 48: 88–91. JSTOR 2684253.

[1]

[2]

Cumulative distribution function

Normality tests

Table of numerical values

See also

References

External links