Circles of Apollonius

Original article: wikipedia:Circles of Apollonius

아폴로니우스의 원(circle of Apollonius)은 유명한 그리스(Greek) 기하학자(geometer)인 페르게의 아폴로니우스(Apollonius of Perga)와 관련된 여러 유형의 원 중에 하나입니다. 이들 원의 대부분은 평면(planar) 유클리드 기하학(Euclidean geometry)에서 발견되지만, 아날로그는 다른 표면에서 정의되어 왔습니다; 예를 들어 구의 표면에 있는 대응물은 입체 투영(stereographic projection)을 통해 정의될 수 있습니다.

이 용어의 주요 용도는 다섯 가지입니다:

1. 아폴로니우스(Apollonius)는 원이 초점(foci)으로 알려진 두 개의 고정 점의 거리의 지정된 비율(ratio)을 갖는 평면 위의 점들의 집합으로 정의될 수 있음을 보였습니다. 이런 "아폴로니우스 원(Apollonian circles)"은 아폴로니우스 추적 문제의 기초입니다. #2에서 설명한 첫 번째 유형의 특별한 사례입니다.
2. 아폴로니우스 원(Apollonian circles)은 서로 직교(orthogonal)하는 원의 두 가족입니다. 첫 번째 가족은 두 고정된 초점에 대한 모든 가능한 거리 비율을 갖는 원으로 구성되며 (#1과 같은 동일한 원), 반면에 두 번째 가족은 초점 둘 다를 통과하는 모든 가능한 원으로 구성됩니다. 이들 원은 이극 좌표(bipolar coordinates)의 기초를 형성합니다.
3. 삼각형의 아폴로니우스의 원은 세 원이며, 그것의 각각은 삼각형의 한 꼭짓점을 통과하고 다른 두 꼭짓점에 대한 거리의 비율을 일정하게 유지합니다. 삼각형의 등역학 점(isodynamic point)과 레모인 직선(Lemoine line)은 이들 아폴로니우스 원을 사용하여 해결될 수 있습니다.
4. 아폴로우스의 문제(Problem of Apollonius)는 세 개의 지정된 원에 동시에 접하는 원을 구성하는 것입니다. 이 문제에 대한 해는 때때로 아폴로니우스의 원으로 불립니다.
5. 아폴로니우스 개스킷(Apollonian gasket)—지금까지 묘사된 최초의 프랙탈(fractal) 중 하나—은 반복적으로 아폴로니우스의 문제를 해결함으로써 형성되는 서로 접하는 원의 집합입니다.

Apollonius' definition of a circle

Main article: Circle § Circle of Apollonius

Figure 1. Apollonius' definition of a circle.

원은 보통 주어진 점 (원의 중심)으로부터 주어진 거리 r (원의 반지름)에서 점 P의 집합으로 정의됩니다. 어쨌든, 원에 대한 다른 동등한 정의가 있습니다. 아폴로니우스는 원이 두 주어진 점 (그림에서 A와 B로 이름-붙인)에 대한 거리 k = d₁/d₂의 주어진 비율을 갖는 점 P의 집합으로 정의될 수 있음을 발견했습니다. 이들 두 점은 때때로 초점(foci)으로 불립니다.

Proof using vectors in Euclidean spaces

d₁, d₂를 비-같은 양의 실수로 놓습니다. C를 비율 d₁ : d₂에서 AB의 내부 분할 점으로 놓고 D를 같은 비율, d₁ : d₂에서 AB의 외부 분할 점으로 놓습니다.

${\overrightarrow {\mathrm {PC} }}={\frac {d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}+d_{1}}},\ {\overrightarrow {\mathrm {PD} }}={\frac {d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}-d_{1}}}.$

그런-다음,

$\mathrm {PA} :\mathrm {PB} =d_{1}:d_{2}.$

$\Leftrightarrow d_{2}|{\overrightarrow {\mathrm {PA} }}|=d_{1}|{\overrightarrow {\mathrm {PB} }}|.$

$\Leftrightarrow d_{2}^{2}|{\overrightarrow {\mathrm {PA} }}|^{2}=d_{1}^{2}|{\overrightarrow {\mathrm {PB} }}|^{2}.$

$\Leftrightarrow (d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }})\cdot (d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }})=0.$

$\Leftrightarrow {\frac {d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}+d_{1}}}\cdot {\frac {d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}-d_{1}}}=0.$

$\Leftrightarrow {\overrightarrow {\mathrm {PC} }}\cdot {\overrightarrow {\mathrm {PD} }}=0.$

$\Leftrightarrow {\overrightarrow {\mathrm {PC} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PD} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PC} }}\perp {\overrightarrow {\mathrm {PD} }}.$

$\Leftrightarrow \mathrm {P} =\mathrm {C} \vee \mathrm {P} =\mathrm {D} \vee \angle {\mathrm {CPD} }=90^{\circ }.$

그러므로, 점 P는 지름 CD을 가지는 원 위에 있습니다.

Proof using the angle bisector theorem

Proof of Apollonius' definition of a circle

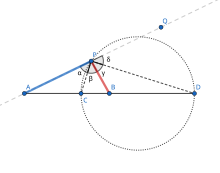
먼저 비율을 만족시키는 $A$와 $B$ 사이의 선분 위의 점 $C$를 생각해 보십시오. 정의에 의해 $${\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}$$ 그리고 각도 이등분선 정리(angle bisector theorem)로부터 각도 $\alpha =\angle APC$와 $\beta =\angle CPB$는 같습니다.

다음으로 비율을 만족시키는 연장된 직선 $AB$의 다른 점 $D$를 취합니다. 따라서 $${\frac {|AP|}{|BP|}}={\frac {|AD|}{|BD|}}.$$ 역시 연장된 직선 $AP$의 아무 곳에서나 어떤 다른 점 $Q$를 취합니다. 역시 각도 이등분선 정리에 의해 직선 $PD$는 외부 각도 $\angle QPB$를 이등분합니다. 따라서, $\gamma =\angle BPD$와 $\delta =\angle QPD$는 같고 $\beta +\gamma =90^{\circ }$입니다. 그러므로 탈레스의 정리(Thales's theorem)에 의해 $P$는 $CD$를 지름으로 가지는 원 위에 놓입니다.

Apollonius pursuit problem

아폴로니우스 추적 문제는 속력 v_A에서 한 지점 A에서 출발하는 배가 속력 v_B에서 다른 점 B를 떠나는 또 다른 배와 교차할 위치를 찾는 것 중 하나입니다. 두 배의 최소-시간 교차는 직선 경로에 의한 것입니다. 만약 배의 속력이 일정하게 유지되면, 그들의 속력 비율은 μ에 의해 정의됩니다. 만약 두 배가 미래 점, I에서 충돌 또는 만나면, 각각의 거리는 다음 방정식에 의해 관련됩니다:

$a=\mu b$

양쪽 변을 제곱하여, 우리는 다음을 얻습니다:

$a^{2}=b^{2}\mu ^{2}$

$a^{2}=x^{2}+y^{2}$

$b^{2}=(d-x)^{2}+y^{2}$

$x^{2}+y^{2}=[(d-x)^{2}+y^{2}]\mu ^{2}$

전개하여:

$x^{2}+y^{2}=[d^{2}+x^{2}-2dx+y^{2}]\mu ^{2}$

뒤따른 전개:

$x^{2}+y^{2}=x^{2}\mu ^{2}+y^{2}\mu ^{2}+d^{2}\mu ^{2}-2dx\mu ^{2}$

왼쪽 변으로 가져오면:

$x^{2}-x^{2}\mu ^{2}+y^{2}-y^{2}\mu ^{2}-d^{2}\mu ^{2}+2dx\mu ^{2}=0$

인수화하여:

$x^{2}(1-\mu ^{2})+y^{2}(1-\mu ^{2})-d^{2}\mu ^{2}+2dx\mu ^{2}=0$

$1-\mu ^{2}$로 나누면

$x^{2}+y^{2}-{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}+{\frac {2dx\mu ^{2}}{1-\mu ^{2}}}=0$

제곱식을 완성하면:

$\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}-{\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}-{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}+y^{2}=0$

비-제곱된 항을 오른쪽 변으로 가져가면:

${\begin{aligned}\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}+y^{2}&={\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}+{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}\\&={\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}+{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}{\frac {(1-\mu ^{2})}{(1-\mu ^{2})}}\\&={\frac {d^{2}\mu ^{4}+d^{2}\mu ^{2}-d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}\\&={\frac {d^{2}\mu ^{2}}{(1-\mu ^{2})^{2}}}\end{aligned}}$

그런-다음:

$\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}+y^{2}=\left({\frac {d\mu }{1-\mu ^{2}}}\right)^{2}$

그러므로, 그 점은 초점으로 그들의 출발 점을 갖는, 아폴로니우스에 의해 정의된 것처럼 원 위에 반드시 놓입니다.

Circles sharing a radical axis

Main article: Apollonian circles

Figure 2. A set of Apollonian circles. Every blue circle intersects every red circle at a right angle, and vice versa. Every red circle passes through the two foci, which correspond to points A and B in Figure 1.

같은 두 점 A와 B이지만, 두 속력의 변하는 비율을 갖는 아폴로니우스 추적 문제에 의해 정의된 원은 서로로부터 분리되고 전체 평면을 덮는 연속 가족을 형성합니다; 원의 이 가족은 쌍곡선 연필로 알려져 있습니다. 원의 또 다른 가족, A와 B 둘 다를 통과하는 원은 연필, 또는 보다 구체적으로 타원 연필으로 역시 불립니다. 아폴로니우스 원(Apollonian circles)의 이들 두 연필은 직각(right angle)에서 서로 교차하고 쌍극 좌표 시스템(bipolar coordinate system)의 기초를 형성합니다. 각 연필 이내에서, 임의의 두 원은 같은 근의 축(radical axis)을 가집니다; 두 연필의 두 제곱근 축은 수직이고, 한 연필로부터 원의 중심은 나머지 연필의 제곱근 축 위에 놓입니다.

Solutions to Apollonius' problem

Main article: Problem of Apollonius

Apollonius' problem may have up to eight solutions. The three given circles are shown in black, whereas the solution circles are colored.

유클리드 평면 기하학(Euclidean plane geometry)에서, 아폴로니우스의 문제는 평면에서 세 주어진 원에 접하는(tangent) 원(circle)을 구성하는 것입니다.

세 주어진 원은 일반적으로 그들에 접하는 여덟 다른 원을 가지고 각 해 원은 다른 방법에서 세 주어진 원을 에워싸거나 배제합니다: 각 해에서, 세 원의 다른 부분-집합이 에워쌉니다.

Apollonian gasket

Main article: Apollonian gasket

Figure 4. A symmetrical Apollonian gasket, also called the Leibniz packing, after its inventor Gottfried Leibniz.

내접원을 찾기 위해 아폴로니우스의 문제를 반복적으로 해결함으로써, 상호 접하는 원 사이의 틈새(interstice)는 임의적으로 세밀하게 채워질 수 있으며, 라이프니츠 패킹(Leibniz packing) 또는 아폴로니우스 패킹(Apollonian packing)으로 역시 알려진 아폴로니우스 개스킷(Apollonian gasket)을 형성합니다. 이 개스킷은 자기-유사이고 정확하게 알려져 있지 않지만 대략 1.3인 차원(dimension) d를 가지는 프랙탈(fractal)이며, 이것은 정규(regular) (또는 정류-가능(rectifiable)) 곡선 (d = 1)보다 더 높지만 평면 (d = 2)의 차원보다는 작습니다. 아폴로니우스 개스킷은 17세기에서 고트프리트 라이프니츠(Gottfried Leibniz)에 의해 처음 설명되었고, 20세기 시에르핀스키 삼각형(Sierpiński triangle)의 곡선화 선구자입니다. 아폴로니우스 개스킷은 수학의 다른 분야와 역시 깊은 관계를 가집니다; 예를 들어, 그것은 클라인 그룹(Kleinian group)의 극한 집합입니다; 그리고 원 패킹 정리(Circle packing theorem)를 역시 참조하십시오.

Isodynamic points of a triangle

아폴로니우스의 원은 임의의 삼각형 $\mathrm {A_{1}A_{2}A_{3}}$에 의해 정의된 세 개의 특수한 원 ${\mathcal {C}}_{1},{\mathcal {C}}_{2},{\mathcal {C}}_{3}$을 역시 나타낼 수 있습니다. 원 ${\mathcal {C}}_{1}$은 나머지 두 꼭짓점 $\mathrm {A_{2}}$와 $\mathrm {A_{3}}$에 대한 거리의 상수 비율을 유지하는 삼각형 꼭짓점 $\mathrm {A_{1}}$을 통과하는 고유한 원으로 정의됩니다 (위에서 원(circle)의 아폴로니우스의 정의를 참조하십시오). 비슷하게, 원 ${\mathcal {C}}_{2}$은 나머지 두 꼭짓점 $\mathrm {A_{1}}$과 $\mathrm {A_{3}}$에 대한 거리의 상수 비율을 유지하는 삼각형 꼭짓점 $\mathrm {A_{2}}$을 통과하는 고유한 원으로 정의되고, ${\mathcal {C}}_{3}$에 대해 마찬가지로 정의됩니다.

모든 세 원은 직교(orthogonal)적으로 삼각형(triangle)의 둘레-원(circumcircle)과 교차합니다. 모든 세 원은 삼각형의 등역학 점(isodynamic point) $S$와 $S^{\prime }$으로 알려진 두 점을 통과합니다. 이들 공통 교차점을 연결하는 직선은 모든 세 원의 근의 축(radical axis)입니다. 두 등역학 점은 삼각형의 둘레-원에 대한 서로 역(inverses)입니다.

이들 세 원의 중심은 한 직선, 즉 레모인 직선(Lemoine line) 위에 떨어집니다. 이 선은 제곱근 축에 수직이며, 이것은 등역학 점에 의해 결정되는 직선입니다.

See also

• Apollonius point

Bibliography

• Ogilvy, C.S. (1990) Excursions in Geometry, Dover. ISBN 0-486-26530-7.
• Johnson, R.A. (1960) Advanced Euclidean Geometry, Dover.