Circle

Original article: wikipedia:Circle

This article is about the shape and mathematical concept. For other uses, see Circle (disambiguation).

"360 degrees" and "360°" redirect here. For other uses, see 360 degrees (disambiguation).

Circle
A circle (black), which is measured by its circumference (C), diameter (D) in blue, and radius (R) in red; its centre (O) is in green.
Type	Conic section
Symmetry group	O(2)
Area	πR2
Perimeter	C = 2πR

원(circle)은 주어진 점, 중심(center)으로부터 주어진 거리에 있는 평면(plane) 안의 모든 점(points)으로 구성된 모양(shape)입니다; 동등하게, 그것은 주어진 점으로부터 거리가 상수(constant)가 되도록 평면에서 움직이는 점에 의해 추적되는 곡선입니다. 원의 점과 중심 사이의 거리는 반지름(radius)으로 불립니다. 이 기사는 유클리드 기하학(Euclidean geometry)에서 원에 대한 것이고, 달리 언급되지 않은 한, 특히 유클리드 평면의 원에 대한 것입니다.

구체적으로, 원은 평면을 두 개의 부위(regions): 내부(interior)와 외부(exterior)로 나누는 단순한(simple) 닫힌 곡선(curve)입니다. 일상적 사용에서, 용어 "원"은 그림의 경계, 또는 그의 내부를 포함하는 전체 그림을 가리키는 것에 상호-교환적으로 사용될 수 있을 것입니다; 엄격한 기술적인 사용에서, 원은 오직 경계일 뿐이고 전체 그림은 디스크(disc)로 불립니다.

원은 두 초점(focus)이 일치하고 이심률(eccentricity)이 0인 타원(ellipse)의 특수한 종류, 또는 변화의 계산법(calculus of variations)을 사용하여 제곱된 단위 둘레 당 최대 넓이를 에워싸는 이-차원 모양으로 정의될 수 있습니다.

Euclid's definition

원은 하나의 곡선으로 경계진 평면 그림이고, 그것 안의 특정 점에서 경계 선까지 그려진 모든 직선이 같은 것을 만족하는 것입니다. 그 경계 선은 그의 원주로 불리고 그 점은 그의 중심으로 불립니다.

— 유클리드(Euclid), 원론(Elements), I 권

Terminology

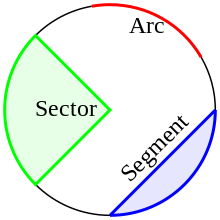
• 원-고리(Annulus): 고리-모양 물체, 영역은 두 동심(concentric) 원에 의해 경계집니다.
• 호(Arc): 원의 임의의 연결된(connected) 부분. 호의 두 끝점과 중심을 지정함은 두 호에 대해 함께 완전한 원을 만드는 것을 허용합니다.
• 중심(Center): 원 위의 모든 점으로부터 같은 거리의 점.
• 현(Chord): 끝점이 원 위에 놓이는 선분, 따라서 원을 두 부분으로 나눕니다.
• 원의-둘레(Circumference): 원을 따라 한 바퀴의 길이, 또는 원 주위의 거리.
• 지름(Diameter): 끝점이 원 위에 놓이고 중심을 통과하는 선분; 또는 그러한 선분의 길이. 이것은 원 위의 임의의 두 점 사이의 가장-큰 거리입니다. 그것은 현의 특별한 경우, 즉 주어진 원에 대해 가장-긴 현이고, 그의 길이는 반지름의 두 배입니다.
• 디스크(Disc): 원에 의해 경계진 평면의 부분.
• 렌즈(Lens): 두 겹치는 디스트에 대한 공통 부분 (교차 부분).
• 패송(Passant): 원과 공통으로 점을 가지지 않는 공통-평면(coplanar) 직선.
• 반지름(Radius): 원의 중심과 원 자체 위의 임의의 한 점을 연결하는 선분; 또는 그러한 선분의 길이, 이것은 지름(의 길이)의 절반입니다.
• 부채꼴(Sector): 이 중심과 반지름의 끝점에 의해 결정된, 하나의 공통 중심과 가진 같은 길이의 두 반지름과 두 가능한 호 중 하나에 의해 경계진 부분.
• 활꼴(Segment): 현과 현의 끝점을 연결하는 호 중 하나로 경계진 부분. 현의 길이는 가능한 호의 지름에 더 낮은 경계를 부과합니다. 때때로 용어 활꼴은 그들 호가 속한 것에 원의 중심을 포함하지 않는 부분에 대해 오직 사용됩니다.
• 가름선(Secant): 두 점에서 원을 교차하는, 연장된 현, 같은-평면 직선.
• 반-원(Semicircle): 중심으로 그의 중간-점을 취하는, 지름의 끝점에 의해 결정된 두 가능한 호 중의 하나. 비-기술적 공통 사용법에서, 그것은 지름과 그 호 중 하나에 의해 경계진 이-차원 부분의 내부를 의미할 수 있습니다, 즉 기술적으로 반-디스크(disc)로 불립니다. 반-디스크는 활꼴(segment)의 특별한 경우, 즉 가장 큰 활꼴입니다.
• 접선(Tangent): 원과 공통으로 오직 하나의 점을 가지는 같은-평면 직선 ("그 점에서 원과 접하는" 직선).

지정된 영역의 모두는 열린 것, 즉, 그들의 경계를 포함하지 않는 것으로 여겨지거나, 각각 그들의 경계를 포함하는 닫힌 것으로 여길 수 있습니다.

Chord, secant, tangent, radius, and diameter

Arc, sector, and segment

History

The compass in this 13th-century manuscript is a symbol of God's act of Creation. Notice also the circular shape of the halo.

단어 circle은 그리스어(Greek) κίρκος/κύκλος (kirkos/kuklos)에서 파생되었으며, 그 자체는 "hoop" 또는 "ring"을 의미하는, 호메릭 그리스어(Homeric Greek) κρίκος (krikos)의 음위전환(metathesis)입니다. 단어 circus 및 circuit의 기원은 밀접하게 관련됩니다.

Circular piece of silk with Mongol images

Circles in an old Arabic astronomical drawing.

원은 기록된 역사의 시작 전부터 알려져 왔습니다. 자연스러운 원은 달, 태양, 및 모래 위에 바람에 날리는 짧은 식물 줄기, 이것은 모래에서 원 모양을 형성된 것에서 관찰되어 왔을 것입니다. 원은 바퀴(wheel)에 대해 기초이며, 이것은, 기어(gear)와 같은 관련된 발명과 함께, 가능한 현대 기계의 많은 것을 만듭니다. 수학에서 원의 연구는 기하학, 천문학(astronomy) 및 미적분학의 발전에 영감을 불어 넣어 왔습니다.

초기 과학(science), 특히 기하학(geometry) 및 점성술과 천문학(astrology and astronomy)은 대부분 중세 학자들(medieval scholars)에 대해 신학자와 연결되었었고, 많은 사람들은 원에서 발견될 수 있는 본질적으로 "신성한" 또는 "완벽한" 어떤 것이 있었다고 믿었습니다.

원의 역사에서 몇 가지 중요한 부분은 다음입니다:

• 기원전 1700 – 린드 파피루스는 원형 들판의 넓이를 찾기 위한 방법을 제공합니다. 그 결과는 π의 대략적인 값으로 256/81 (3.16049...)에 해당합니다.

Tughrul Tower from inside

• 기원전 300 – 유클리드 원론(Euclid's Elements)의 책 3은 원의 속성을 다룹니다.
• 플라톤(Plato)의 일곱 번째 편지(Seventh Letter)에서, 원의 자세한 정의와 설명이 있습니다. 플라톤은 완벽한 원을 설명하고, 그것이 임의의 그림, 단어, 정의 또는 설명과 어떻게 다른지 설명합니다.
• 기원후 1880 – 린데만(Lindemann)은 π가 초월적(transcendental)이라는 것을 입증하여, 천년간-오랜된 원을 정사각형화(squaring the circle)의 문제를 효과적으로 해결합니다.

Analytic results

Length of circumference

Further information: Circumference

원의 둘레(circumference)와 지름(diameter)의 비율은 π (pi), 대략 3.141592654와 같은 무리(irrational) 상수(constant)입니다. 따라서 원-둘레 C의 길이는 다음에 의해 반지름 r과 지름 d와 관련됩니다:

$C=2\pi r=\pi d.\,$

Area enclosed

Area enclosed by a circle = π × area of the shaded square

Main article: Area of a circle

아르키메데스(Archimedes)에 의해 입증된 것처럼, 그의 원의 측정(Measurement of a Circle)에서, 원으로 둘러싸인 넓이는 원의 둘레의 길이를 가지는 밑변과 원의 반지름과 같은 높이를 가지는 삼각형의 넓이와 같으며, 이것은 π에 제곱된 반지름을 곱한 것이 됩니다:

$\mathrm {Area} =\pi r^{2}.\,$

동등하게, d로 지름을 표시하면,

$\mathrm {Area} ={\frac {\pi d^{2}}{4}}\approx 0{.}7854d^{2},$

그것은 외접하는(circumscribing) 정사각형 (변은 길이 d의 것입니다)의 대략 79%입니다.

원은 주어진 호 길이에 대해 최대 넓이를 둘러싸는 평면 곡선입니다. 이것은 원을 변화의 계산법(calculus of variations)에서 한 문제, 즉 같은-둘레 부등식(isoperimetric inequality)과 관련시킵니다.

Equations

Cartesian coordinates

Circle of radius r = 1, centre (a, b) = (1.2, −0.5)

Equation of a circle
x–y 데카르트 좌표 시스템(Cartesian coordinate system)에서, 중심 좌표(coordinates) (a, b) 및 반지름 r을 갖는 원은 다음을 만족하는 모든 점 (x, y)의 집합입니다:

$\left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}.$

원의 방정식으로 알려진 이 방정식(equation)은 원 위의 임의의 점에 적용된 피타고라스 정리(Pythagorean theorem)로부터 따릅니다: 인접한 그림에서 보이는 것처럼, 반지름은 직각 삼각형의 대각선에 있고 다른 두 변은 길이 |x − a| 및 |y − b|의 것입니다. 만약 원이 원점 (0, 0)에 중심을 두면, 방정식은 다음으로 단순해집니다:

$x^{2}+y^{2}=r^{2}.\!\$

Parametric form
방정식은 다음으로 삼각 함수(trigonometric function) 사인 및 코사인을 사용하여 매개-변수 형식(parametric form)으로 쓸 수 있습니다:

$x=a+r\,\cos t,\,$

$y=b+r\,\sin t\,$

여기서 t는 범위 0에서 2π까지에서 매개-변수(parametric variable)이며, (a, b)에서 (x, y)까지 반직선이 양의 x-축과 만드는 각도(angle)로 기하학적으로 해석됩니다.

원의 대안적인 매개-변수화는 다음입니다:

$x=a+r{\frac {1-t^{2}}{1+t^{2}}}.\,$

$y=b+r{\frac {2t}{1+t^{2}}}\,$

이 매개-변수화에서, r에 대한 t의 비율은 x-축에 평행한 중심을 통과하는 직선의 입체 투영(stereographic projection)으로 기하학적으로 해석될 수 있습니다 (탄젠트 반-각 치환(Tangent half-angle substitution)을 참조하십시오). 어쨌든, 이 매개-변수화는 만약 t가 모든 실수를 통한 범위 뿐만 아니라 무한대에서 점까지 범위에 대해 만들어지면 오직 작동합니다; 그렇지 않으면, 원의 가장-왼쪽 점이 생략될 것입니다.

3-point-form
한 직선 위에 있지 않는 세 점 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$에 의해 결정된 원의 방정식은 원의 방정식의 3-점-형식(3-point-form of a circle's equation)의 변환에 의해 얻습니다:

${\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.$

Homogeneous form
동차 좌표(homogeneous coordinates)에서, 원의 방정식을 갖는 각 원뿔 단면(conic section)은 다음 형식을 가집니다:

$x^{2}+y^{2}-2axz-2byz+cz^{2}=0.\,$

그것은, 원뿔 단면은, 그것이 점 I(1: i: 0) 및 J(1: −i: 0)를 포함할 때 (복소 투영 평면(complex projective plane)으로 확장될 때), 정확히 하나의 원임을 입증될 수 있습니다. 이들 점은 무한대에서 원형 점(circular points at infinity)으로 불립니다.

Polar coordinates

극 좌표(polar coordinates)에서, 원의 방정식은 다음입니다:

$r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{2}\,$

여기서 a는 원의 반지름, $(r,\theta )$는 원 위의 일반적인 점의 극 좌표이고, $(r_{0},\phi )$는 원의 중심의 극 좌표입니다 (즉, r₀는 원점에서 원의 중심까지 거리이고, φ는 양의 x-축에서 원점을 원의 중심에 연결하는 직선까지 반-시계방향 각도입니다). 원점에 중심을 둔 원, 즉, r₀ = 0에 대해, 이것은 단순히 r = a로 축소합니다. r₀ = a일 때, 또는 원점이 원 위에 놓일 때, 방정식은 다음이 됩니다:

$r=2a\cos(\theta -\phi ).\,$

일반적인 경우에서, 방정식은 r에 대해 해결될 수 있으며, 다음을 제공합니다:

$r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\theta -\phi )}},$

± 부호없이, 방정식은 일부 경우에서 오직 원의 절반을 묘사할 뿐임에 주목하십시오.

Complex plane

복소 평면(complex plane)에서, c에 중심 및 반지름 r을 가진 원은 다음 방정식을 가집니다:

$|z-c|=r\,$.

매개-변수 형식(parametric form)에서, 이것은 다음으로 쓸 수 있습니다:

$z=re^{it}+c$.

실수 p, q 및 복소수 g에 대해 약간 일반화된 방정식

$pz{\overline {z}}+gz+{\overline {gz}}=q$

은 때때로 일반화된 원(generalised circle)으로 불립니다. 이것은 $p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}$을 갖는 원에 대해 위의 방정식이 되는데, 왜냐하면 $|z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}$입니다. 모든 일반화된 원이 실제로 원은 아닙니다: 일반화된 원은 (진짜) 원 또는 직선(line) 중에 하나입니다.

Tangent lines

Main article: Tangent lines to circles

원 위의 점 P를 통과하는 접선(tangent line)은 P를 통과하는 지름과 수직입니다. 만약 P = (x₁, y₁)이고 원의 중심 (a, b)를 가지고 반지름 r이면, 접선은 (a, b)에서 (x₁, y₁)까지 직선과 수직이므로, 그것은 형식 (x₁ − a)x + (y₁ – b)y = c을 가집니다. (x₁, y₁)에서 평가함으로써 c의 값이 결정되고 그 결과는 접선의 방정식이 다음인 것입니다:

$(x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1}\,$

또는

$(x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}.\!\$

만약 y₁ ≠ b이면, 그 직선의 기울기는 다음입니다:

${\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}.$

이것은 암시적 미분(implicit differentiation)을 사용하여 역시 찾아질 수 있습니다.

원의 중심이 원점에 있을 때, 접선의 방정식은 다음이 됩니다:

$x_{1}x+y_{1}y=r^{2},\!\$

및 그의 기울기는 다음입니다:

${\frac {dy}{dx}}=-{\frac {x_{1}}{y_{1}}}.$

Properties

• 원은 주어진 둘레의 길이에서 가장 큰 넓이를 가진 모양입니다. (같은-둘레 불평등(Isoperimetric inequality)을 참조하십시오.)
• 원은 매우 대칭적인 모양입니다: 중심을 통과하는 모든 직선은 반사 대칭(reflection symmetry)의 직선을 형성하고 그것은 모든 각 각도에 대해 중심 주위에 회전 대칭(rotational symmetry)을 가집니다. 그것의 대칭 그룹(symmetry group)은 직교 그룹(orthogonal group) O(2,R)입니다. 회전의 그룹 단독으로 원 그룹(circle group) T입니다.
• 모든 원은 닮은(similar) 것입니다.
  • 원의 둘레와 반지름은 비례적(proportional)입니다.
  • 둘러싸인 넓이(area)와 그의 반지름의 제곱은 비례적(proportional)입니다.
  • 비례의 상수(constants)는 각각 2π 및 π입니다.
• 반지름 1을 가진 원에 중심을 둔 원은 단위 원(unit circle)으로 불립니다.
  • 단위 구(unit sphere)의 큰 원(great circle)으로 생각하면, 그것은 리만 원(Riemannian circle)이 됩니다.
• 모두가 같은 직선 위에 있지 않은, 임의의 세 점을 통해, 고유한 원에 놓입니다. 데카르트 좌표(Cartesian coordinates)에서, 주어진 세 점의 좌표의 관점에서 원의 중심의 좌표와 반지름에 대한 명시적 공식을 제공할 수 있습니다. 둘레-원(circumcircle)를 참조하십시오.

Chord

• 현이 원의 중심으로부터 같은 거리에 있는 것은 그들이 길이에서 같은 것과 필요충분 조건입니다.
• 현의 수직 이등분선(perpendicular bisector)은 원의 중심을 통과합니다; 수직 이등분선의 고유성에서 유래되는 동등한 명제는 다음입니다:
  • 원의 중심으로부터 수직 직선은 현을 이등분합니다.
  • 현을 이둥분하는 중심을 통과하는 선분(line segment)은 그 현에 수직(perpendicular)입니다.
• 만약 원의 중심 각과 내접 각(inscribed angle)이 같은 현에 의해 끼워지고 현의 같은 쪽에 놓이면, 중심 각은 내접 각의 두 배입니다.
• 만약 두 각도가 같은 현에 대한 내접된 것이고 현의 같은 쪽에 놓이면, 그들은 같습니다.
• 만약 두 각도가 같은 현에 대한 내접된 것이고 현의 반대 쪽에 놓이면, 그들은 보충각(supplementary)입니다.
  • 순환 사변형(cyclic quadrilateral)에 대해, 외부 각도(exterior angle)는 내부 반대 각도와 같습니다.
• 지름에 의해 끼워진 내접 각도는 직각입니다 (탈레스의 정리(Thales' theorem)를 보십시오).
• 지름은 원의 가장-긴 현입니다.
  • 공통으로 현 AB를 갖는 모든 원 사이에서, 최소 반지름을 갖는 원은 지름 AB를 가진 원입니다.
• 만약 임의의 두 현의 교차(intersection of any two chords)가 한 현을 길이 a와 b로 나누고 나머지 한 현을 길이 c와 d로 나누면, ab = cd입니다.
• 만약 임의의 두 수직 현의 교차는 한 현을 길이 a와 b로 나누고 나머지 한 현을 길이 c와 d로 나누면, a² + b² + c² + d²는 지름의 제곱과 같습니다.
• 주어진 점에서 직각으로 교차하는 임의의 두 현의 제곱된 길이의 합은 같은 점에서 교차하는 임의의 다른 두 수직 현의 그것과 같고, 8r ² – 4p ²으로 제공됩니다 (여기서 r은 원의 반지름이고 p는 중심 점으로부터 교차의 점까지 거리입니다).
• 원 위의 한 점으로부터 주어진 현까지 거리 곱하기 원의 지름은 그 점으로부터 현의 끝점들까지 거리들의 곱과 같습니다.

Tangent

• 원 위에 놓이는 반지름의 끝점을 통해 반지름에 수직으로 그려진 직선은 원에 접합니다.
• 원과 접하는 점을 통해 접선에 수직으로 그려진 직선은 원의 중심을 통과합니다.
• 두 접선은 원 밖의 임의의 점에서 원에 그려질 수 있고, 이들 접선의 길이는 같습니다.
• 만약 A에서 접선과 B에서 접선이 외부 점 P에서 교차하면, 중심을 O로 표시하면, 각도 ∠BOA와 ∠BPA는 보충각(supplementary)입니다.
• 만약 AD가 A에서 원에 접하고 만약 AQ가 원의 현이면, ∠DAQ = 1/2arc(AQ)입니다.

Theorems

Secant-secant theorem

See also: Power of a point

• 현 정리는, 만약 두 현, CD와 EB가 A에서 교차하면, AC × AD = AB × AE.라고 말합니다.
• 만약 두 가름선, AE와 AD가 각각 B와 C에서 각각 원을 역시 자르면, AC × AD = AB × AE입니다. (현 정리의 따름정리(Corollary))
• 접선은 끝이 일치하는 가름선의 극한적인 경우로 여길 수 있습니다. 만약 외부 점 A로부터 접선(tangent)이 F에서 원과 만나고 외부 점 A로부터 가름선(secant)이 각각 C와 D에서 원과 만나면, AF² = AC × AD입니다. (접선-가름선 정리.)
• 현과 그의 끝점 중 하나에서 접선 사이의 각도는, 현의 대변 위에서 (접선 현 각도), 원의 중심에서 끼워진 각도의 절반과 같습니다.
• 만약 중심에서 현에 끼워진 각도가 90 도(degrees)이면 ℓ = r √2이며, 여기서 ℓ는 현의 길이이고 r은 원의 반지름입니다.
• 만약 두 가름선이, 오른쪽에 보인 것처럼, 원 안에 새겨져 있으면, 각도 A의 측정은 에워싸는 호 (${\overset {\frown }{DE}}$ 및 ${\overset {\frown }{BC}}$)의 측정의 차이의 절반과 같습니다. 즉, $2\angle {CAB}=\angle {DOE}-\angle {BOC}$이며, 여기서 O는 원의 중심입니다. 이것이 가름선-가름선 정리입니다.

Inscribed angles

See also: Inscribed angle theorem

Inscribed angle theorem

내접 각(inscribed angle) (예제는 그림에서 파란색과 녹색 각도)은 해당하는 중심 각(central angle) (빨간색)의 정확히 절반입니다. 그러므로, 같은 호 (분홍색)에 끼워진 모든 내접 각은 같습니다. 호 (갈색)에 내접된 각도는 보충각입니다. 특히, 지름(diameter)에 끼워진 모든 각 내접 각은 직각(right angle)입니다 (왜냐하면 중심 각은 180도이기 때문입니다).

Sagitta

The sagitta is the vertical segment.

• 화살(sagitta) (역시 벌사인(versine)으로 알려짐)은, 해당 현의 중간 점과 원의 호 사이에, 현에 수직으로 그려진 선분입니다.
• 현의 길이 y 및 화살의 길이 x가 주어지면, 피타고라스 정리(Pythagorean theorem)는 두 선분 주위에 맞을 수 있는 고유한 원의 반지름을 계산하기 위해 사용될 수 있습니다:

$r={\frac {y^{2}}{8x}}+{\frac {x}{2}}.$

위에 주어진 두 현 속성에 오직 의존하는, 이 결과의 또 다른 증며은 다음의 것입니다. 길이 y의 현과 함께 길이 x의 화살이 주어지면, 화살이 현의 중간-점과 교차하므로, 우리는 그것이 원의 지름의 일부임을 알고 있습니다. 지름은 반지름의 두 배이므로, 지름의 "누락된" 부분은 길이에서 (2r − x)입니다. 한 현의 한 부분 곱하기 나머지 한 부분은 첫 번째 현과 교차하는 현에서 취한 동일한 곱과 같다는 사실을 사용함으로써, 우리는 (2r − x)x = (y / 2)²임을 찾습니다. r에 대해 풀면, 우리는 요구된 결과를 찾습니다.

Compass and straightedge constructions

컴퍼스-와-직선자 구성(compass-and-straightedge construction)의 결과로 생기는 많은 원이 있습니다.

가장-단순하고 가장 기초적인 것은 원의 중심과 원 위의 한 점이 주어진 구성입니다. 컴퍼스(compass)의 고정된 다리를 중심 점 위에 놓고, 움직일 수 있는 다리를 원 위의 그 점에 놓고 컴퍼스를 돌리십시오.

Construction with given diameter

• 지름의 중간-점(midpoint) M을 구성하십시오.
• 지름의 끝점 중 하나를 통과하는 중심 M을 가진 원을 구성하십시오 (그것은 나머지 한 끝 점을 역시 통과할 것입니다).

Construct a circle through points A, B and C by finding the perpendicular bisectors (red) of the sides of the triangle (blue). Only two of the three bisectors are needed to find the centre.

Construction through three noncollinear points

• 점 P, Q 및 R을 지정하십시오.
• 선분 PQ의 수직 이등분선(perpendicular bisector)을 구성하십시오.
• 선분 PR의 수직 이등분선(perpendicular bisector)을 구성하십시오.
• 이들 두 수직 이등분선 M의 교차의 점을 레이블을 붙이십시오 (그들은 만나는데 왜냐하면 점들은 같은-직선(collinear) 위에 있지 않기 때문입니다).
• 점 P, Q 또는 R 중 하나를 통과하는 중심 M을 가진 원을 구성하십시오 (그것은 나머지 두 점을 역시 통과할 것입니다).

Circle of Apollonius

See also: Circles of Apollonius

Apollonius' definition of a circle: d₁/d₂ constant

페르가의 아폴로니우스(Apollonius of Perga)는 원이 두 고정된 초점, A 및 B에 대한 거리의 (1 이외의) 일정한 비율을 갖는 평면에서 점의 집합으로 역시 정의될 수 있음을 보였습니다. (거리가 같은 점들의 집합은 선분 AB, 한 직선의 수직 이등분선입니다.) 해당 원은 때때로 두 점에 대해 그려졌다고 말합니다.

증명은 두 부분으로 구성되어 있습니다. 먼저, 우리는, 두 초점 A와 B 및 거리의 비율이 주어지면, 거리의 비율을 만족시키는 임의의 점 P는 특정 원 위에 있어야 함을 증명해야 합니다. C를, 역시 비율을 만족시키고 선분 AB 위에 놓인, 또 다른 점으로 놓습니다. 각도 이등분 정리(angle bisector theorem)에 의해 선분 PC는 내부 각도(interior angle) APB를 이등분할 것인데, 왜냐하면 그 선분들은 닮은 것이기 때문입니다:

${\frac {AP}{BP}}={\frac {AC}{BC}}.$

유사하게, 연장된 AB 위에 어떤 점 D를 통한 선분 PD는 대응하는 외부 각도(exterior angle) BPQ를 이등분하며, 여기서 Q는 연장된 AP 위에 있습니다. 내부 및 외부 각도는 합해져서 180도이므로, 각도 CPD는 정확히 90도, 즉, 직각(right angle)입니다. 각도 CPD가 직각을 만족하는 점 P의 집합은 원을 형성하며, 그것의 CD는 지름입니다.

둘째, 표시된 원 위의 모든 각 점이 주어진 비율을 만족시키는 증명을 보십시오.

Cross-ratios

원의 밀접하게 관련된 속성은 복소 평면(complex plane)에서 점의 교차-비율(cross-ratio)의 기하학을 포함합니다. 만약 A, B, 및 C가 위와 같으면, 이들 세 점에 대한 아폴로니우스의 원은 교차-비율의 절댓값이 1과 같은 것에 대해 점 P의 모음입니다:

$|[A,B;C,P]|=1.\$

또 다른 방법으로 말하면, P가 아폴로니우스 원 위의 한 점인 것과 교차-비율 [A,B;C,P]은 복소 평면에서 단위 원(unit circle) 위에 있는 것은 필요충분 조건입니다.

Generalised circles

See also: Generalised circle

만약 C가 선분 AB의 중간-점(midpoint)이면, 아폴로니우스 조건

${\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}$ 

을 만족시키는 점 P의 모음은 원이 아니지만, 차라리 직선입니다.

따라서, 만약 A, B, 및 C가 평면에서 주어진 구별되는 점이면, 위의 방정식을 만족시키는 점 P의 궤적은 "일반화된 원"으로 불립니다. 그것은 참 원 또는 직선 중에 하나일 수 있습니다. 이 의미에서 직선(line)은 무한한 반지름의 일반화된 원입니다.

Inscription in or circumscription about other figures

내원(incircle)으로 불리는, 모든 각 삼각형(triangle)에서 고유한 원은, 그것이 삼각형의 세 변 각각에 접하는 것을 만족하는, 내접되는 것입니다.

둘레-원(circumcircle)으로 불리는, 모든 각 삼각형에 대한 고유한 원은, 그것이 삼각형의 세 꼭짓점(vertices)의 각각을 지나는 것을 만족하는, 외접하는 것입니다.

접하는 사변형(tangential quadrilateral)과 같은, 접하는 다각형(tangential polygon)은 그것 안에 다각형의 각 변에 접하는 원이 내접될 수 있는 임의의 볼록 다각형(convex polygon)입니다. 모든 각 정규 다각형(regular polygon) 및 모든 각 삼각형은 접하는 다각형입니다.

순환 다각형(cyclic polygon)은, 각 꼭짓점을 통과하여, 원이 그것에 대해 외접되어 있는 볼록 다각형입니다. 잘-연구된 예제는 순환 사각형(cyclic quadrilateral)입니다. 모든 각 정규 다각형 및 모든 각 삼각형은 순환 다각형입니다. 순환 및 접하는 둘 다인 다각형은 쌍-중심 다각형(bicentric polygon)으로 불립니다.

하이포-사이클로이드(hypocycloid)는 주어진 원에 접하고 그 안에서 구르는 더 작은 원 위에 고정된 점을 추적함으로써 주어진 원 안에 새겨진 곡선입니다.

Limiting case of other figures

원은 여러 다른 그림의 각각의 극한적인 경우(limiting case)로 보일 수 있습니다:

• 데카르트 달걀형(Cartesian oval)은 임의의 그의 점으로부터 두 고정된 점 (초점(foci))까지 거리의 가중된 합(weighted sum)이 상수인 것을 만족하는 점의 집합입니다. 타원(ellipse)은 가중값이 같은 경우입니다. 원은 영의 이심률(eccentricity)을 가진 타원으며, 두 초점이 원의 중심으로 서로 일치함을 의미합니다. 원은 역시 가중값의 하나가 영인 데카르트 달걀형의 다른 특수한 경우입니다.
• 초-타원(superellipse)은 양의 a, b, 및 n에 대해 형식 $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$의 방정식을 가집니다. 초-타원은 b = a을 가집니다. 원은 n = 2인 것에서 초-타원의 특별한 경우입니다.
• 카시니 달걀형(Cassini oval)은 임의의 그 점으로부터 두 고정된 점까지 거리의 곱이 상수인 것을 만족하는 점의 집합입니다. 두 고정 점이 일치하면 원이 생성됩니다.
• 한 점에서 그의 경계를 교차하는 각각 두 구별되는 평행 직선 사이의 수직 거리로 정의된, 상수 폭의 곡선(curve of constant width)은 그의 폭이 그들의 두 평행 직선의 방향에 관계없이 같은 그림입니다. 원은 이러한 유형의 그림 중 가장 간단한 예제입니다.

In other p-norms

Illustrations of unit circles (see also superellipse) in different p-norms (every vector from the origin to the unit circle has a length of one, the length being calculated with length-formula of the corresponding p).

원을 한 점으로부터 고정된 거리를 가진 점의 집합으로 정의하면, 다른 모양은 거리의 다른 정의 아래에서 원으로 여길 수 있습니다. p-노름(p-norm)에서, 거리는 다음에 의해 결정됩니다:

$\left\|x\right\|_{p}=\left(|x_{1}|^{p}+|x_{2}|^{p}+\dotsb +|x_{n}|^{p}\right)^{1/p}.$

유클리드 기하학에서, p = 2이며, 다음의 익숙한 것을 제공합니다:

$\left\|x\right\|_{2}={\sqrt {|x_{1}|^{2}+|x_{2}|^{2}+\dotsb +|x_{n}|^{2}}}.$

택시캡 기하학(taxicab geometry)에서, p = 1입니다. 택시캡 원은 좌표축에 대해 45° 각도로 향한 변을 가진 정사각형(squares)입니다. 각 변의 길이는 유클리드 메트릭(Euclidean metric)을 사용하여, r이 원의 반지름일 때, 길이 ${\sqrt {2}}r$를 갖지만, 택시캡 기하학에서 그의 길이는 2r입니다. 따라서, 원의 둘레는 8r입니다. 따라서, $\pi$에 대한 기하학적 아날로그의 값은, 이 기하학에서, 4입니다. 택시캡 기하학에서 단위 원에 대한 공식은 데카르트 좌표(Cartesian coordinates)에서 $|x|+|y|=1$이고, 극 좌표(polar coordinates)에서 다음입니다:

$r={\frac {1}{|\sin \theta |+|\cos \theta |}}$.

반지름 1 (이 거리를 사용하여)의 원은 그의 중의 폰 노이만 이웃(von Neumann neighborhood)입니다.

평면에서 체비쇼프 거리(Chebyshev distance) (L_∞ 메트릭)에 대해 반지름 r의 원은 좌표 축에 평행한 변 길이 2r을 가진 정사각형이므로, 평면 체비쇼프 거리는 평면 택시캡 거리에 대한 회전 및 스케일링함으로써 동등한 것으로 보일 수 있습니다. 어쨌든, L₁ 및 L_∞ 메트릭 사이의 이 동등성은 더 높은 차원에 대해 일반화되지 않습니다.

Squaring the circle

Main article: Squaring the circle

원을 정사각형화(Squaring the circle)는, 고대(ancient) 기하학자(geometers)에 의해 제안된, 문제로 컴퍼스와 직선자(compass and straightedge)와 함께 오직 유한한 숫자의 단계를 사용하여 주어진 원과 같은 넓이의 정사각형을 구성하는 것입니다.

1882년에, 그 과제는, 린데만-바이어슈트라스 정리(Lindemann-Weierstrass theorem)의 결과로 인해, 불가능한 것으로 입증이 되었으며, 그것은 pi (π)가 대수적 무리수(algebraic irrational number)라기 보다는 초월적 숫자(transcendental number)임을 입증한 것입니다; 즉, 그것은 유리(rational) 계수를 가진 임의의 다항식(polynomial)의 근(root)이 아닙니다.

Significance in art and symbolism

아시리아인과 고대 이집트인, 인더스 계곡과 중국의 황하에서 그들, 및 고전적 유물 시대 동안 고대 그리스와 로마의 서구 문명와 같은 가장-초기 알려진 문명의 시대로부터, 원은 시각 예술에서 작가의 메시지를 전달하고 특정 아이디어를 표현하기 위해 간접 또는 간접적으로 사용되어 왔습니다. 어쨌든, 세계관 (믿음과 문화)의 차이는 예술가의 인식에 큰 영향을 미쳤습니다. 어떤 사람들은 민주주의적 표현을 보여주기 위해 원의 둘레를 강조했지만, 다른 사람들은 우주 통일의 개념을 상징하기 위해 중심에 집중했습니다. 신비로운 교리에서, 원은 주로 존재의 무한하고 주기적 본질을 상징하지만, 종교적 전통에서 그것은 천체와 신령을 나타냅니다. 원은 다른 것들 중에서도 화합, 무한성, 완전성, 우주, 신성, 균형, 안정 및 완전성을 포함하여, 많은 신성한 영적 개념을 나타냅니다. 그러한 개념은, 예를 들어, 나침반, 후광, 방광 물고기 및 그 파생물 (물고기, 눈, 아우레올, 만돌라, 등), 우로보로스, 달마 휠, 무지개, 만다라, 장미 창문 및 기타 등등과 같은 기호의 사용을 통해 전-세계 문화에서 전달되어 왔습니다.

See also

• Affine sphere
• Annulus (mathematics)
• Apeirogon
• Circle fitting
• List of circle topics
• Sphere
• Three points determine a circle
• Translation of axes

Specially named circles

• Unit circle
• Apollonian circles
• Chromatic circle
• Ford circle
• Circle of antisimilitude
• Carlyle circle
• Bankoff circle
• Archimedes' twin circles
• Archimedean circle
• Johnson circles
• Schoch circles
• Woo circles

Of a triangle

• Mandart circle
• Spieker circle
• Nine-point circle
• Lemoine circle
• Circumcircle
• Incircle
• Excircle
• Apollonius circle of the excircles
• Lester circle
• Malfatti circles
• Brocard circle
• Orthocentroidal circle
• Van Lamoen circle
• Parry circle
• Polar circle (geometry)

Of certain quadrilaterals

• Eight-point circle of an orthodiagonal quadrilateral
• Incircle of a tangential quadrilateral
• Circumcircle of a cyclic quadrilateral

Of certain polygons

• Circumcircle of a cyclic polygon
• Incircle of a tangential polygon

Of a conic section

• Director circle
• Directrix circle

Of a sphere

• Great circle
• Riemannian circle

Of a torus

• Villarceau circles

Further reading

• Pedoe, Dan (1988). Geometry: a comprehensive course. Dover.
• "Circle" in The MacTutor History of Mathematics archive

External links

• "Circle", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Circle (PlanetMath.org website)
• Weisstein, Eric W. "Circle". MathWorld.
• "Interactive Java applets". for the properties of and elementary constructions involving circles
• "Interactive Standard Form Equation of Circle". Click and drag points to see standard form equation in action
• "Munching on Circles". cut-the-knot