Cylindrical coordinate system

Original article: w:Cylindrical coordinate system

A cylindrical coordinate system with origin O, polar axis A, and longitudinal axis L. The dot is the point with radial distance ρ = 4, angular coordinate φ = 130°, and height z = 4.

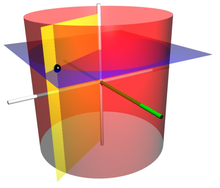
원통 좌표 시스템(cylindrical coordinate system)은 선택된 참조 축 (옆의 이미지에서 축 L)으로부터의 거리, 선택된 참조 방향 (축 A)에 상대적인 축으로부터의 방향, 및 축에 수직인 선택된 참조 평면 (보라색 부분을 포함하는 평면)으로부터의 거리에 의해 점 위치를 지정하는 삼-차원 좌표 시스템(coordinate system)입니다. 후자의 거리는 참조 평면의 어느 면이 점을 향하는지에 따라 양수 또는 음수로 지정됩니다.

시스템의 원점(origin)은 모든 세 좌표가 영으로써 주어질 수 있는 점입니다. 이것은 참조 평면과 축 사이의 교차점입니다. 축은 원점에서 시작하고 참조 방향을 향하는 참조 평면에 놓여있는 반직선(ray)인 극축(polar axis)과 그것을 구별하기 위해 원통(cylindrical) 또는 경도(longitudinal) 축으로 다양하게 불립니다. 경도 축에 수직인 다른 방향은 방사형 직선(radial lines)이라고 불립니다.

축으로부터 거리는 방사형 거리(radial distance) 또는 반지름(radius)이라고 불릴 수 있고, 반면에 각도 좌표는 때때로 각도 위치(angular position) 또는 방위각(azimuth)으로 참조됩니다. 반지름과 방위각은 함께 극 좌표(polar coordinates)라고 불리는데, 왜냐하면 그것들은 참조 평면에 평행한 점을 통해 평면에서 이-차원 극 좌표(polar coordinate) 시스템에 해당하기 때문입니다. 세 번째 좌표는 높이(height) 또는 고도(altitude) (만약 기본 평면이 수평으로 고려되면), 경도 위치(longitudinal position), 또는 축 위치(axial position)라고 불릴 수 있습니다.

원통 좌표는 둥근 횡-단면을 갖는 직선 관의 물의 흐름, 금속 원기둥(cylinder)에서 열 분포, 길고 긴 철선에 흐르는 전류(electric current)에 의해 생성된 전자기 필드(electromagnetic fields), 천문학에서 응축 디스크(accretion disk), 기타 등등과 같은 경도 축에 대한 일부 회전 대칭(symmetry)을 가지는 대상과 현상과 관련하여 유용합니다.

그것들은 때때로 "원통 극 좌표" 및 "극 원통 좌표"라고 불리고, 은하에서 별의 위치를 지정하기 위해서 때때로 사용됩니다 ("글렉토센트릭 원통 극 좌표(galactocentric cylindrical polar coordinate)").

Definition

점 P의 세 좌표 (ρ, φ, z)는 다음과 같이 정의됩니다:

• 축 거리(axial distance) 또는 방사형 거리(radial distance) ρ는 z-축에서 점 P까지의 유클리드 거리입니다.
• 방위각(azimuth) φ는 선택된 평면의 참조 방향과 원점에서 평면 위의 P의 투영까지의 직선 사이의 각도입니다.
• 축 좌표(axial coordinate) 또는 높이(height) z는 선택된 평면에서 점 P까지의 부호화된 거리입니다.

Unique cylindrical coordinates

극 좌표에서와 같이, 원통 좌표 (ρ, φ, z)를 갖는 같은 점은 무한하게 많은 동등한 좌표, 즉 (ρ, φ ± n×360°, z)와 (−ρ, φ ± (2n + 1)×180°, z)를 가지며, 여기서 n은 임의의 정수입니다. 게다가, 만약 반지름 ρ가 영이면 방위각은 임의적입니다.

누군가가 각 점에 대한 고유한 좌표의 집합을 원하는 상황에서, 반지름을 비-음수 (ρ ≥ 0)로 제한하고 방위각 φ를 [−180°,+180°] 또는 [0,360°]와 같이 360°을 스팬하는 특정 구간에 놓이도록 제한할 수 있습니다.

Conventions

원통 좌표에 대한 표기법은 균등하지 않습니다. ISO 표준 31-11은 (ρ, φ, z)를 권장하며, 여기서 ρ는 방사형 좌표, φ는 방위각, z는 높이입니다. 어쨌든, 반지름은 역시 종종 r 또는 s로, 방위각은 θ 또는 t로, 및 세 번째 좌표는 h 또는 (원통 축이 수평으로 고려되면) x, 또는 임의의 문맥-별 문자로 표시되기도 합니다.

The coordinate surfaces of the cylindrical coordinates (ρ, φ, z). The red cylinder shows the points with ρ = 2, the blue plane shows the points with z = 1, and the yellow half-plane shows the points with φ = −60°. The z-axis is vertical and the x-axis is highlighted in green. The three surfaces intersect at the point P with those coordinates (shown as a black sphere); the Cartesian coordinates of P are roughly (1.0, −1.732, 1.0).

Cylindrical coordinate surfaces. The three orthogonal components, ρ (green), φ (red), and z (blue), each increasing at a constant rate. The point is at the intersection between the three colored surfaces.

구체적인 상황과 많은 수학적 설명에서, 양의 각도 좌표는 양의 높이를 갖는 임의의 점에서 볼 때 반시계방향(counterclockwise)으로 측정됩니다.

Coordinate system conversions

원통 좌표 시스템은 많은 삼-차원 좌표 시스템 중 하나입니다. 다음 수식은 그것들 사이를 변환하기 위해 사용될 수 있습니다.

Cartesian coordinates

원통 좌표와 데카르트 좌표 사이의 변환을 위해, 전자의 참조 평면이 데카르트 xy-평면 (방정식 z = 0을 가짐)이고, 원통 축이 데카르트 z-축이라고 가정하는 것이 편리합니다. 그런-다음 z-좌표는 두 시스템에서 같고, 원통 좌표 (ρ, φ, z)와 데카르트 좌표 (x, y, z) 사이의 대응은 극 좌표에 대한 것과 같습니다. 즉, 한 방향에서 $${\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}$$ 그리고, 다른 방향에서, $${\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &={\begin{cases}{\text{indeterminate}}&{\text{if }}x=0{\text{ and }}y=0\\\arcsin \left({\frac {y}{\rho }}\right)&{\text{if }}x\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y<0\end{cases}}\end{aligned}}$$ 아크사인(arcsine) 함수는 사인 함수의 역이고, [−π/2, +π/2] = [−90°, +90°] 범위에서 각도를 반환하는 것으로 가정합니다. 이들 공식은 [−90°, +270°] 범위에서 방위각 φ를 산출합니다.

역시 [−π/2, +π/2] = [−90°, +90°] 범위에서 각도를 반환하는 아크탄젠트(arctangent) 함수를 사용함으로써, 먼저 $\rho$를 계산 없이 $\varphi$를 계산할 수도 있습니다: $${\begin{aligned}\varphi &={\begin{cases}{\text{indeterminate}}&{\text{if }}x=0{\text{ and }}y=0\\{\frac {\pi }{2}}{\frac {y}{|y|}}&{\text{if }}x=0{\text{ and }}y\neq 0\\\arctan \left({\frac {y}{x}}\right)&{\mbox{if }}x>0\\\arctan \left({\frac {y}{x}}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y\geq 0\\\arctan \left({\frac {y}{x}}\right)-\pi &{\mbox{if }}x<0{\text{ and }}y<0\end{cases}}\end{aligned}}$$ 다른 공식에 대해, 극 좌표 시스템(Polar coordinate system) 기사를 참조하십시오.

많은 최신 프로그래밍 언어는 위와 같은 사례 분석을 수행할 필요 없이, x와 y가 주어지면, (−π, π) 범위에서 올바른 방위각 φ를 계산하는 함수를 제공합니다. 예를 들어, 이 함수는 C 프로그래밍 언어에서 atan2(y, x)와 Common Lisp의 atan(y, x)에 의해 호출됩니다.

Spherical coordinates

구형 좌표(Spherical coordinates, 반지름 r, 고도 또는 기울기 θ, 방위각 φ)는 다음에 의해 원통 좌표로 변환될 수 있습니다:

θ is elevation:	θ is inclination:
${\begin{aligned}\rho &=r\cos \theta \\\varphi &=\varphi \\z&=r\sin \theta \end{aligned}}$	${\begin{aligned}\rho &=r\sin \theta \\\varphi &=\varphi \\z&=r\cos \theta \end{aligned}}$

원통 좌표는 다음에 의해 구형 좌표로 변환될 수 있습니다:

θ is elevation:	θ is inclination:
${\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}}\\\theta &=\arctan \left({\tfrac {z}{\rho }}\right)\\\varphi &=\varphi \end{aligned}}$	${\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}}\\\theta &=\arctan \left({\tfrac {\rho }{z}}\right)\\\varphi &=\varphi \end{aligned}}$

Line and volume elements

See multiple integral for details of volume integration in cylindrical coordinates, and Del in cylindrical and spherical coordinates for vector calculus formulae.

원통형 극 좌표와 관련한 많은 문제에서, 직선과 부피 원소를 아는 것이 유용합니다; 이것들은 경로와 부피와 관련된 문제를 해결하기 위해 적분에서 사용됩니다.

선 적분(line element)은 다음과 같습니다:

$\mathrm {d} {\boldsymbol {r}}=\mathrm {d} \rho \,{\boldsymbol {\hat {\rho }}}+\rho \,\mathrm {d} \varphi \,{\boldsymbol {\hat {\varphi }}}+\mathrm {d} z\,{\boldsymbol {\hat {z}}}.$

부피 원소(volume element)는 다음과 같습니다:

$\mathrm {d} V=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi \,\mathrm {d} z.$

일정한 반지름 ρ의 표면 (수직 원기둥)에서 표면 원소(surface element)는 다음과 같습니다:

$\mathrm {d} S_{\rho }=\rho \,\mathrm {d} \varphi \,\mathrm {d} z.$

일정한 방위각 φ 의 표면 (수직 절반-평면)의 표면 원소는 다음과 같습니다:

$\mathrm {d} S_{\varphi }=\mathrm {d} \rho \,\mathrm {d} z.$

일정한 높이 z의 표면 (수평 평면)에서 표면 원소는 다음과 같습니다:

$\mathrm {d} S_{z}=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi .$

이 시스템에서 델(del) 연산자는 그래디언트(gradient), 다이버전스(divergence), 컬(curl), 및 라플라스(Laplacian)에 대한 다음 표현으로 이어집니다:

${\begin{aligned}\nabla f&={\frac {\partial f}{\partial \rho }}{\boldsymbol {\hat {\rho }}}+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}{\boldsymbol {\hat {\varphi }}}+{\frac {\partial f}{\partial z}}{\boldsymbol {\hat {z}}}\\[8px]\nabla \cdot {\boldsymbol {A}}&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho A_{\rho }\right)+{\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}\\[8px]\nabla \times {\boldsymbol {A}}&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\boldsymbol {\hat {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\boldsymbol {\hat {\varphi }}}+{\frac {1}{\rho }}\left({\frac {\partial }{\partial \rho }}\left(\rho A_{\varphi }\right)-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\boldsymbol {\hat {z}}}\\[8px]\nabla ^{2}f&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial f}{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}f}{\partial \varphi ^{2}}}+{\frac {\partial ^{2}f}{\partial z^{2}}}\end{aligned}}$

Cylindrical harmonics

원통 대칭을 갖는 시스템에서 라플라스 방정식에 대한 해는 원통형 고조파(cylindrical harmonics)라고 불립니다.

Kinematics

원통형 좌표 시스템에서, 입자의 위치는 다음과 같이 쓸 수 있습니다: $${\boldsymbol {r}}=\rho \,{\boldsymbol {\hat {\rho }}}+z\,{\boldsymbol {\hat {z}}}.$$ 입자의 속도는 그것의 위치의 시간 도함수입니다: $${\boldsymbol {v}}={\frac {\mathrm {d} {\boldsymbol {r}}}{\mathrm {d} t}}={\dot {\rho }}\,{\boldsymbol {\hat {\rho }}}+\rho \,{\dot {\varphi }}\,{\hat {\boldsymbol {\varphi }}}+{\dot {z}}\,{\hat {\boldsymbol {z}}},$$ 여기서 항 $\rho {\dot {\varphi }}{\hat {\varphi }}$은 푸아송 공식 ${\frac {\mathrm {d} {\hat {\rho }}}{\mathrm {d} t}}={\dot {\varphi }}{\hat {z}}\times {\hat {\rho }}$에서 나옵니다. 그것의 가속도는 다음과 같습니다: $${\boldsymbol {a}}={\frac {\mathrm {d} {\boldsymbol {v}}}{\mathrm {d} t}}=\left({\ddot {\rho }}-\rho \,{\dot {\varphi }}^{2}\right){\boldsymbol {\hat {\rho }}}+\left(2{\dot {\rho }}\,{\dot {\varphi }}+\rho \,{\ddot {\varphi }}\right){\hat {\boldsymbol {\varphi }}}+{\ddot {z}}\,{\hat {\boldsymbol {z}}}$$

See also

• List of canonical coordinate transformations
• Vector fields in cylindrical and spherical coordinates
• Del in cylindrical and spherical coordinates

Further reading

• Morse, Philip M.; Feshbach, Herman (1953). Methods of Theoretical Physics, Part I. New York City: McGraw-Hill. pp. 656–657. ISBN 0-07-043316-X. LCCN 52011515.
• Margenau, Henry; Murphy, George M. (1956). The Mathematics of Physics and Chemistry. New York City: D. van Nostrand. p. 178. ISBN 9780882754239. LCCN 55010911. OCLC 3017486.
• Korn, Granino A.; Korn, Theresa M. (1961). Mathematical Handbook for Scientists and Engineers. New York City: McGraw-Hill. pp. 174–175. LCCN 59014456. ASIN B0000CKZX7.
• Sauer, Robert; Szabó, István (1967). Mathematische Hilfsmittel des Ingenieurs. New York City: Springer-Verlag. p. 95. LCCN 67025285.
• Zwillinger, Daniel (1992). Handbook of Integration. Boston: Jones and Bartlett Publishers. p. 113. ISBN 0-86720-293-9. OCLC 25710023.
• Moon, P.; Spencer, D. E. (1988). "Circular-Cylinder Coordinates (r, ψ, z)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed.). New York City: Springer-Verlag. pp. 12–17, Table 1.02. ISBN 978-0-387-18430-2.

External links

• "Cylinder coordinates", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• MathWorld description of cylindrical coordinates
• Cylindrical Coordinates Animations illustrating cylindrical coordinates by Frank Wattenberg