수학(mathematics) 의 한 가지, 실수 해석학(real analysis) 에서, 다르부 적분 은 다르부 합 을 사용하여 구성되고 함수(function) 의 적분(integral) 의 하나의 가능한 정의입니다. 다르부 적분은, 함수가 다르부-적분가능인 것과 그것이 리만-적분가능인 것이 필요충분 조건이고, 두 적분의 값이 그것들이 존재하면 같다는 의미에서 리만 적분(Riemann integral) 과 동등합니다.[1] 미적분학(calculus) 과 실수 해석학에 대한 입문 교과서는 종종 실제 리만 적분이라기 보다는 다르부 적분을 사용하여 리만 적분을 개발합니다.[2] 리만–스틸티어스 적분(Riemann–Stieltjes integration) 을 정의하는 것으로 쉽게 확장됩니다.[3] 개스통 다르부(Gaston Darboux) 의 이름을 따서 지어졌습니다.
Definition 다르부 적분의 정의는 구간(interval)
[
a
,
b
]
{\displaystyle [a,b]}
경계진(bounded) 실수(real) -값 함수
f
{\displaystyle f}
위쪽 및 아래쪽 (다르부) 적분 을 고려합니다. 다르부 적분 이 존재하는 것과 위쪽 및 아래쪽 적분이 같은 것은 필요충분 조건입니다. 위쪽 및 아래쪽 적분은 차례로 각각 "곡선 아래의 넓이"를 과대- 및 과소평가하는 위쪽 및 아래쪽 (다르부) 합 의, 각각, 하한과 상한(infimum and supremum) 입니다. 특히, 적분 구간의 주어진 분할에 대해, 위쪽과 아래쪽 합은 그것의 높이가 분할의 각 부분구간에서 각각 f 의 상한과 하한인 직사각형 얇은 조각의 넓이를 함께 더합니다. 이들 아이디어는 아래에 보다 정확하게 만듭니다:
Darboux sums 구간
[
a
,
b
]
{\displaystyle [a,b]}
은 다음을 만족하는 값 x i
a
=
x
0
<
x
1
<
⋯
<
x
n
=
b
.
{\displaystyle a=x_{0}<x_{1}<\cdots <x_{n}=b.}
각 구간 [x i −1x i 부분구간 (subinterval )이라고 불립니다. f : [a , b ] → R 를 경계진 함수로 놓고, 다음을
P
=
(
x
0
,
…
,
x
n
)
{\displaystyle P=(x_{0},\ldots ,x_{n})}
[a , b ]의 분할로 놓습니다. 다음이라고 놓습니다:
M
i
=
sup
x
∈
[
x
i
−
1
,
x
i
]
f
(
x
)
,
m
i
=
inf
x
∈
[
x
i
−
1
,
x
i
]
f
(
x
)
.
{\displaystyle {\begin{aligned}M_{i}=\sup _{x\in [x_{i-1},x_{i}]}f(x),\\m_{i}=\inf _{x\in [x_{i-1},x_{i}]}f(x).\end{aligned}}}
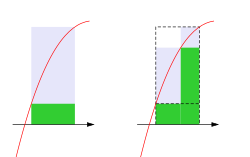
Lower (green) and upper (green plus lavender) Darboux sums for four subintervals P 에 관한 f 의 위쪽 다르부 합 은 다음입니다:
U
f
,
P
=
∑
i
=
1
n
(
x
i
−
x
i
−
1
)
M
i
.
{\displaystyle U_{f,P}=\sum _{i=1}^{n}(x_{i}-x_{i-1})M_{i}.\,\!}
P 에 관한 f 의 아래쪽 다르부 합 은 다음입니다:
L
f
,
P
=
∑
i
=
1
n
(
x
i
−
x
i
−
1
)
m
i
.
{\displaystyle L_{f,P}=\sum _{i=1}^{n}(x_{i}-x_{i-1})m_{i}.\,\!}
아래쪽과 위쪽 다르부 합은 종종 아래쪽과 위쪽 합이라고 불립니다.
Darboux integrals f 의 위쪽 다르부 적분 은 다음입니다:
U
f
=
inf
{
U
f
,
P
:
P
is a partition of
[
a
,
b
]
}
.
{\displaystyle U_{f}=\inf\{U_{f,P}\colon P{\text{ is a partition of }}[a,b]\}.\,\!}
f 의 아래쪽 다르부 적분 은 다음입니다:
L
f
=
sup
{
L
f
,
P
:
P
is a partition of
[
a
,
b
]
}
.
{\displaystyle L_{f}=\sup\{L_{f,P}\colon P{\text{ is a partition of }}[a,b]\}.\,\!}
일부 문헌에서 밑줄과 윗줄을 갖는 적분 기호는 각각 아래쪽과 위쪽 다르부 적분을 나타냅니다.
L
f
≡
∫
a
b
_
f
(
x
)
d
x
U
f
≡
∫
a
b
¯
f
(
x
)
d
x
,
{\displaystyle {\begin{aligned}L_{f}\equiv {\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\\[6pt]U_{f}\equiv {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x,\end{aligned}}}
그리고 다르부 합처럼 그것들은 때때로 단순히 아래쪽과 위쪽 적분이라고 불립니다.
만약 U f L f 다르부 적분 이라고 부릅니다.[4] f 가 다르부-적분가능 또는 단순히 적분-가능 이고 다음으로 놓는다고 말합니다.
∫
a
b
f
(
t
)
d
t
=
U
f
=
L
f
,
{\displaystyle \int _{a}^{b}{f(t)\,dt}=U_{f}=L_{f},}
f 의 적분가능성에 대해 동등하고 때때로 유용한 기준은 모든 각 ε > 0에 대해, 다음을 만족하는 [a , b ]의 분할 P ε 이 존재한다는 것을 보여주는 것입니다:[5]
U
f
,
P
ϵ
−
L
f
,
P
ϵ
<
ε
.
{\displaystyle U_{f,P_{\epsilon }}-L_{f,P_{\epsilon }}<\varepsilon .}
Properties 임의의 주어진 분할에 대해, 위쪽 다르부 합은 항상 아래쪽 다르부 합보다 크거나 같습니다. 게다가, 낮은 다르부 합은 [a , b ]에 걸쳐 취해진 너비 (b −a )와 높이 inf(f )의 직사각형에 의해 아래로 경계진 것입니다. 마찬가지로, 위쪽 합은 너비 (b −a )와 높이 sup(f )의 직사각형에 의해 위로 경계진 것입니다.
(
b
−
a
)
inf
x
∈
[
a
,
b
]
f
(
x
)
≤
L
f
,
P
≤
U
f
,
P
≤
(
b
−
a
)
sup
x
∈
[
a
,
b
]
f
(
x
)
{\displaystyle (b-a)\inf _{x\in [a,b]}f(x)\leq L_{f,P}\leq U_{f,P}\leq (b-a)\sup _{x\in [a,b]}f(x)}
아래쪽과 위쪽 다르부 적분은 다음을 만족시킵니다:
∫
a
b
_
f
(
x
)
d
x
≤
∫
a
b
¯
f
(
x
)
d
x
{\displaystyle {\underline {\int _{a}^{b}}}f(x)\,dx\leq {\overline {\int _{a}^{b}}}f(x)\,dx}
(a , b )에서 임의의 c 가 주어지면:
∫
a
b
_
f
(
x
)
d
x
=
∫
a
c
_
f
(
x
)
d
x
+
∫
c
b
_
f
(
x
)
d
x
∫
a
b
¯
f
(
x
)
d
x
=
∫
a
c
¯
f
(
x
)
d
x
+
∫
c
b
¯
f
(
x
)
d
x
{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,dx&={\underline {\int _{a}^{c}}}f(x)\,dx+{\underline {\int _{c}^{b}}}f(x)\,dx\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,dx&={\overline {\int _{a}^{c}}}f(x)\,dx+{\overline {\int _{c}^{b}}}f(x)\,dx\end{aligned}}}
아래쪽과 위쪽 다르부 적분은 반드시 선형은 아닙니다. g :[a , b ] → R 가 역시 경계진 함수라고 가정하면, 위쪽과 아래쪽 적분은 다음 부등식을 만족시킵니다.
∫
a
b
_
f
(
x
)
d
x
+
∫
a
b
_
g
(
x
)
d
x
≤
∫
a
b
_
(
f
(
x
)
+
g
(
x
)
)
d
x
∫
a
b
¯
f
(
x
)
d
x
+
∫
a
b
¯
g
(
x
)
d
x
≥
∫
a
b
¯
(
f
(
x
)
+
g
(
x
)
)
d
x
{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,dx+{\underline {\int _{a}^{b}}}g(x)\,dx&\leq {\underline {\int _{a}^{b}}}(f(x)+g(x))\,dx\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,dx+{\overline {\int _{a}^{b}}}g(x)\,dx&\geq {\overline {\int _{a}^{b}}}(f(x)+g(x))\,dx\end{aligned}}}
상수 c ≥ 0에 대해 우리는 다음을 가집니다:
∫
a
b
_
c
f
(
x
)
=
c
∫
a
b
_
f
(
x
)
∫
a
b
¯
c
f
(
x
)
=
c
∫
a
b
¯
f
(
x
)
{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}cf(x)&=c{\underline {\int _{a}^{b}}}f(x)\\[6pt]{\overline {\int _{a}^{b}}}cf(x)&=c{\overline {\int _{a}^{b}}}f(x)\end{aligned}}}
상수 c ≤ 0에 대해 우리는 다음을 가집니다:
∫
a
b
_
c
f
(
x
)
=
c
∫
a
b
¯
f
(
x
)
∫
a
b
¯
c
f
(
x
)
=
c
∫
a
b
_
f
(
x
)
{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}cf(x)&=c{\overline {\int _{a}^{b}}}f(x)\\[6pt]{\overline {\int _{a}^{b}}}cf(x)&=c{\underline {\int _{a}^{b}}}f(x)\end{aligned}}}
다음 함수를 생각해 보십시오:
F
:
[
a
,
b
]
→
R
F
(
x
)
=
∫
a
x
_
f
(
t
)
d
t
{\displaystyle {\begin{aligned}&{}F:[a,b]\to \mathbb {R} \\&{}F(x)={\underline {\int _{a}^{x}}}f(t)\,dt\end{aligned}}}
F 는 립시츠 연속(Lipschitz continuous) 입니다. 동일한 결과는 만약 F 가 위쪽 다르부 적분을 사용하여 정의되면 유지됩니다. Examples A Darboux-integrable function 우리는 함수 f (x ) = x 가 구간 [0, 1]에서 다르부 적분-가능임을 보이고 그 값을 결정하기를 원한다고 가정합니다. 이것을 하기 위해, 우리는 [0, 1]을 각각 길이 1/n 을 갖는 n 같은 크기의 부분구간으로 분할합니다. 우리는 n 같은 크기의 부분구간의 분할을 P n
이제 f (x ) = x 가 [0, 1]에서 엄격하게 증가하므로, 임의의 특정 부분구간의 하한은 그것의 시작점에 의해 제공됩니다. 마찬가지로 임의의 특정 부분구간의 상한은 그것의 끝점에 의해 제공됩니다. P n k 번째 부분구간의 시작점은 (k −1)/n 이고 끝점은 k /n 입니다. 따라서 파티션 P n
L
f
,
P
n
=
∑
k
=
1
n
f
(
x
k
−
1
)
(
x
k
−
x
k
−
1
)
=
∑
k
=
1
n
k
−
1
n
⋅
1
n
=
1
n
2
∑
k
=
1
n
[
k
−
1
]
=
1
n
2
[
(
n
−
1
)
n
2
]
{\displaystyle {\begin{aligned}L_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k-1})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k-1}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}[k-1]\\&={\frac {1}{n^{2}}}\left[{\frac {(n-1)n}{2}}\right]\end{aligned}}}
유사하게, 위쪽 다르부 합은 다음에 의해 주어집니다:
U
f
,
P
n
=
∑
k
=
1
n
f
(
x
k
)
(
x
k
−
x
k
−
1
)
=
∑
k
=
1
n
k
n
⋅
1
n
=
1
n
2
∑
k
=
1
n
k
=
1
n
2
[
(
n
+
1
)
n
2
]
{\displaystyle {\begin{aligned}U_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}k\\&={\frac {1}{n^{2}}}\left[{\frac {(n+1)n}{2}}\right]\end{aligned}}}
다음이기 때문입니다:
U
f
,
P
n
−
L
f
,
P
n
=
1
n
{\displaystyle U_{f,P_{n}}-L_{f,P_{n}}={\frac {1}{n}}}
따라서 주어진 임의의 ε > 0에 대해, 우리는
n
>
1
ϵ
{\displaystyle n>{\frac {1}{\epsilon }}}
P n
U
f
,
P
n
−
L
f
,
P
n
<
ϵ
{\displaystyle U_{f,P_{n}}-L_{f,P_{n}}<\epsilon }
이것은 f 가 다르부 적분가능임을 보여줍니다. 적분의 값을 구하기 위해 다음임을 주목하십시오:
∫
0
1
f
(
x
)
d
x
=
lim
n
→
∞
U
f
,
P
n
=
lim
n
→
∞
L
f
,
P
n
=
1
2
{\displaystyle \int _{0}^{1}f(x)\,dx=\lim _{n\to \infty }U_{f,P_{n}}=\lim _{n\to \infty }L_{f,P_{n}}={\frac {1}{2}}}
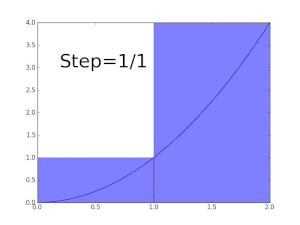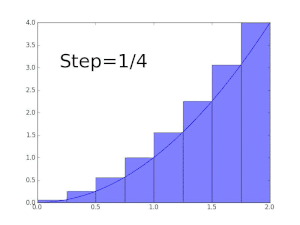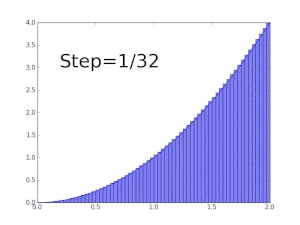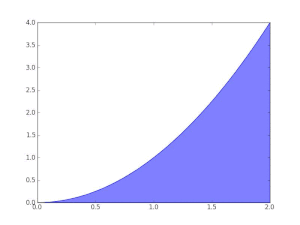
Darboux upper sums of the function y = x 2
Darboux lower sums of the function y = x 2
A nonintegrable function 우리는 함수
f
:
[
0
,
1
]
→
R
{\displaystyle f:[0,1]\to \mathbb {R} }
f
(
x
)
=
{
0
if
x
is rational
1
if
x
is irrational
{\displaystyle {\begin{aligned}f(x)&={\begin{cases}0&{\text{if }}x{\text{ is rational}}\\1&{\text{if }}x{\text{ is irrational}}\end{cases}}\end{aligned}}}
유리수와 무리수는 둘 다 R 의 조밀한 부분집합(dense subset) 이므로, f 는 임의의 분할의 모든 각 부분구간에서 0과 1의 값을 취함을 따릅니다. 따라서 임의의 분할 P 에 대해 우리는 다음을 가집니다:
L
f
,
P
=
∑
k
=
1
n
(
x
k
−
x
k
−
1
)
inf
x
∈
[
x
k
−
1
,
x
k
]
f
=
0
U
f
,
P
=
∑
k
=
1
n
(
x
k
−
x
k
−
1
)
sup
x
∈
[
x
k
−
1
,
x
k
]
f
=
1
{\displaystyle {\begin{aligned}L_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\inf _{x\in [x_{k-1},x_{k}]}f=0\\U_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\sup _{x\in [x_{k-1},x_{k}]}f=1\end{aligned}}}
이것으로부터, 우리는 아래쪽과 위쪽 다르부 적분이 같지 않음을 알 수 있습니다.
Refinement of a partition and relation to Riemann integration When passing to a refinement, the lower sum increases and the upper sum decreases. 분할
x
0
,
…
,
x
n
{\displaystyle x_{0},\ldots ,x_{n}}
세분화 는 모든 i = 0, …, n 에 대해 다음을 만족하는 정수(integer) 가 있음을 만족하는 분할
y
0
,
…
,
y
m
{\displaystyle y_{0},\ldots ,y_{m}}
x
i
=
y
r
(
i
)
.
{\displaystyle x_{i}=y_{r(i)}.}
다시 말해서, 세분화를 만들기 위해, 부분구간을 더 작은 조각으로 자르고 임의의 기존 자름을 제거하지 않습니다.
만약
P
′
=
(
y
0
,
…
,
y
m
)
{\displaystyle P'=(y_{0},\ldots ,y_{m})}
P
=
(
x
0
,
…
,
x
n
)
{\displaystyle P=(x_{0},\ldots ,x_{n})}
U
f
,
P
≥
U
f
,
P
′
{\displaystyle U_{f,P}\geq U_{f,P'}}
및
L
f
,
P
≤
L
f
,
P
′
.
{\displaystyle L_{f,P}\leq L_{f,P'}.}
만약 P 1 , P 2 가 같은 구간의 두 분할이면 (하나가 나머지 하나의 세분화일 필요는 없습니다), 다음이고
L
f
,
P
1
≤
U
f
,
P
2
,
{\displaystyle L_{f,P_{1}}\leq U_{f,P_{2}},}
다음임을 따릅니다:
L
f
≤
U
f
.
{\displaystyle L_{f}\leq U_{f}.}
리만 합은 항상 대응하는 아래쪽과 위쪽 다르부 합 사이에 놓입니다. 형식적으로, 만약
P
=
(
x
0
,
…
,
x
n
)
{\displaystyle P=(x_{0},\ldots ,x_{n})}
T
=
(
t
1
,
…
,
t
n
)
{\displaystyle T=(t_{1},\ldots ,t_{n})}
리만 적분(Riemann integral) 의 정의에서 처럼) 다음 태그-지정된 분할을 만들고:
x
0
≤
t
1
≤
x
1
≤
⋯
≤
x
n
−
1
≤
t
n
≤
x
n
{\displaystyle x_{0}\leq t_{1}\leq x_{1}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}}
만약 P 와 T 에 해당하는
f
{\displaystyle f}
R 이면, 다음입니다:
L
f
,
P
≤
R
≤
U
f
,
P
.
{\displaystyle L_{f,P}\leq R\leq U_{f,P}.}
이전 사실로부터, 리만 적분은 적어도 다르부 적분만큼 강력합니다: 만약 다르부 적분이 존재하면, 충분히 미세한 분할에 해당하는 위쪽과 아래쪽 다르부 합은 적분 값에 가까울 것이므로, 같은 분할에 걸쳐 임의의 리만 합은 역시 적분의 값에 가까울 것입니다. 위쪽 다르부 적분 또는 아래쪽 다르부 적분의 값에 임의적으로 가깝게 되는 태그-지정된 분할이 있고 (아래를 참조), 결과적으로, 만약 리만 적분이 존재하면, 다르부 적분은 마찬가지로 존재해야 합니다.
Details of finding the tags
이 증명에 대해, 우리는 위첨자를
{
P
(
n
)
}
{\displaystyle \left\{P^{(n)}\right\}}
{
P
(
n
)
}
{\displaystyle \left\{P^{(n)}\right\}}
‖
P
n
‖
→
0
{\displaystyle \|P_{n}\|\to 0}
[
a
,
b
]
{\displaystyle [a,b]}
하한의 정의에 의해, 임의의
ϵ
>
0
{\displaystyle \epsilon >0}
inf
x
∈
[
x
i
(
n
)
,
x
i
+
1
(
n
)
]
f
(
x
)
≥
f
(
t
i
(
n
)
)
−
ϵ
{\displaystyle \inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)\geq f(t_{i}^{(n)})-\epsilon }
t
i
(
n
)
∈
[
x
i
(
n
)
,
x
i
+
1
(
n
)
]
{\displaystyle t_{i}^{(n)}\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}
∑
i
=
0
N
(
n
)
−
1
f
(
t
i
)
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
≤
∑
i
=
0
N
(
n
)
−
1
(
inf
x
∈
[
x
i
(
n
)
,
x
i
+
1
(
n
)
]
f
(
x
)
+
ϵ
)
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
=
∑
i
=
0
N
(
n
)
−
1
inf
x
∈
[
x
i
(
n
)
,
x
i
+
1
(
n
)
]
f
(
x
)
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
+
∑
i
=
0
N
−
1
ϵ
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
=
∑
i
=
0
N
(
n
)
−
1
inf
x
∈
[
x
i
(
n
)
,
x
i
+
1
(
n
)
]
f
(
x
)
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
+
ϵ
(
b
−
a
)
.
{\displaystyle {\begin{aligned}\sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})&\leq &\sum _{i=0}^{N^{(n)}-1}\left(\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)+\epsilon \right)(x_{i+1}^{(n)}-x_{i}^{(n)})&\ \ \ \\&=&\sum _{i=0}^{N^{(n)}-1}\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+\sum _{i=0}^{N-1}\epsilon (x_{i+1}^{(n)}-x_{i}^{(n)})\\&=&\sum _{i=0}^{N^{(n)}-1}\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+\epsilon (b-a).\end{aligned}}}
ϵ
=
1
/
n
(
b
−
a
)
{\displaystyle \epsilon =1/n(b-a)}
∑
i
=
0
N
(
n
)
−
1
f
(
t
i
)
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
≤
∑
i
=
0
N
(
n
)
−
1
inf
x
∈
[
x
i
(
n
)
,
x
i
+
1
(
n
)
]
f
(
x
)
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
+
1
n
=
L
f
,
P
(
n
)
+
1
n
{\displaystyle {\begin{aligned}\sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})&\leq &\sum _{i=0}^{N^{(n)}-1}\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+{\frac {1}{n}}\\&=&L_{f,P^{(n)}}+{\frac {1}{n}}\end{aligned}}}
양쪽 변에 극한을 취하면,
R
f
=
∑
i
=
0
N
(
n
)
−
1
f
(
t
i
)
(
x
i
+
1
(
n
)
−
x
i
(
n
)
)
≤
lim
n
→
∞
L
f
,
P
(
n
)
+
lim
n
→
∞
1
n
=
lim
n
→
∞
L
f
,
P
(
n
)
.
{\displaystyle {\begin{aligned}R_{f}=\sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})\leq \lim _{n\to \infty }L_{f,P^{(n)}}+\lim _{n\to \infty }{\frac {1}{n}}=\lim _{n\to \infty }L_{f,P^{(n)}}.\end{aligned}}}
유사하게, (태그의 다른 수열과 함께)
R
f
≥
lim
n
→
∞
U
f
,
P
(
n
)
.
{\displaystyle {\begin{aligned}R_{f}\geq \lim _{n\to \infty }U_{f,P^{(n)}}.\end{aligned}}}
따라서, 우리는 다음을 가집니다:
R
f
≤
lim
n
→
∞
L
f
,
P
(
n
)
≤
lim
n
→
∞
U
f
,
P
(
n
)
≤
R
f
,
{\displaystyle R_{f}\leq \lim _{n\to \infty }L_{f,P^{(n)}}\leq \lim _{n\to \infty }U_{f,P^{(n)}}\leq R_{f},}
이것은 다르부 적분이 존재하고
R
f
{\displaystyle R_{f}}
See also Notes References


![{\displaystyle [a,b]}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle {\begin{aligned}M_{i}=\sup _{x\in [x_{i-1},x_{i}]}f(x),\\m_{i}=\inf _{x\in [x_{i-1},x_{i}]}f(x).\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/c17d20124547d96a57c5e6cd4386d88abaa622a4)


![{\displaystyle U_{f}=\inf\{U_{f,P}\colon P{\text{ is a partition of }}[a,b]\}.\,\!}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/66ef09340fab6ca296c12136fb4c1eedbfc0a393)
![{\displaystyle L_{f}=\sup\{L_{f,P}\colon P{\text{ is a partition of }}[a,b]\}.\,\!}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/f2af06540dcf87c8ff222df795c41c1c447f3177)
![{\displaystyle {\begin{aligned}L_{f}\equiv {\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\\[6pt]U_{f}\equiv {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x,\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/ec186e2108891626ffaba67e50dec6c9644bc1e8)


![{\displaystyle (b-a)\inf _{x\in [a,b]}f(x)\leq L_{f,P}\leq U_{f,P}\leq (b-a)\sup _{x\in [a,b]}f(x)}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/fb367d6382f3b3ea0ed86c0c7c530396f62f06ed)

![{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,dx&={\underline {\int _{a}^{c}}}f(x)\,dx+{\underline {\int _{c}^{b}}}f(x)\,dx\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,dx&={\overline {\int _{a}^{c}}}f(x)\,dx+{\overline {\int _{c}^{b}}}f(x)\,dx\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/91ca354c965e553c119390bdc098498cf6924e2a)
![{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,dx+{\underline {\int _{a}^{b}}}g(x)\,dx&\leq {\underline {\int _{a}^{b}}}(f(x)+g(x))\,dx\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,dx+{\overline {\int _{a}^{b}}}g(x)\,dx&\geq {\overline {\int _{a}^{b}}}(f(x)+g(x))\,dx\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/9424ce17345ffd01d310f81608947a0e695ff49e)
![{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}cf(x)&=c{\underline {\int _{a}^{b}}}f(x)\\[6pt]{\overline {\int _{a}^{b}}}cf(x)&=c{\overline {\int _{a}^{b}}}f(x)\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/b1ff65ffe3c3450e80595904cb27db29579c1bf7)
![{\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}cf(x)&=c{\overline {\int _{a}^{b}}}f(x)\\[6pt]{\overline {\int _{a}^{b}}}cf(x)&=c{\underline {\int _{a}^{b}}}f(x)\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/9d4deb50be8c107001624492038553efef715b7d)
![{\displaystyle {\begin{aligned}&{}F:[a,b]\to \mathbb {R} \\&{}F(x)={\underline {\int _{a}^{x}}}f(t)\,dt\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/e89d7fa934d9a8fc33fd417d4615ce7a192b9960)
![{\displaystyle {\begin{aligned}L_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k-1})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k-1}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}[k-1]\\&={\frac {1}{n^{2}}}\left[{\frac {(n-1)n}{2}}\right]\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/6f9d5136be122292af60763e9e5c1d81fead9972)
![{\displaystyle {\begin{aligned}U_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}k\\&={\frac {1}{n^{2}}}\left[{\frac {(n+1)n}{2}}\right]\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/a8c2c468d5244b9b8e8434d9438d274cb7ecdac1)





![{\displaystyle f:[0,1]\to \mathbb {R} }](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/2de6d0d4c98d4ca7ad937c772dc3e3e914b062f5)

![{\displaystyle {\begin{aligned}L_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\inf _{x\in [x_{k-1},x_{k}]}f=0\\U_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\sup _{x\in [x_{k-1},x_{k}]}f=1\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/e53219a61241091dae7dc2f3a2dfeba19ad209f2)














![{\displaystyle \inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)\geq f(t_{i}^{(n)})-\epsilon }](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/aa9e79adf285ab7a5ebcd8f021b58761dc03043e)
![{\displaystyle t_{i}^{(n)}\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/a12b81d4e986db0a519305d6258a955e5ddc5845)
![{\displaystyle {\begin{aligned}\sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})&\leq &\sum _{i=0}^{N^{(n)}-1}\left(\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)+\epsilon \right)(x_{i+1}^{(n)}-x_{i}^{(n)})&\ \ \ \\&=&\sum _{i=0}^{N^{(n)}-1}\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+\sum _{i=0}^{N-1}\epsilon (x_{i+1}^{(n)}-x_{i}^{(n)})\\&=&\sum _{i=0}^{N^{(n)}-1}\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+\epsilon (b-a).\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/d7bc3cd8ddd03113499be11b700865c547d2e444)

![{\displaystyle {\begin{aligned}\sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})&\leq &\sum _{i=0}^{N^{(n)}-1}\inf _{x\in \left[x_{i}^{(n)},x_{i+1}^{(n)}\right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+{\frac {1}{n}}\\&=&L_{f,P^{(n)}}+{\frac {1}{n}}\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/2c1c663d57858be415105e3e197f145747ce4e0d)



