Dihedral angle

이면체 각도(dihedral angle)는 두 개의 교차하는 평면 사이의 각도입니다. 화학(chemistry)에서, 그것은 두 개의 원자를 공통으로 가지는 세 개의 원자의 두 집합을 통과하는 평면 사이의 각도입니다. 입체 기하학(solid geometry)에서, 그것은 한 직선(line)과 이 직선을 공통 가장자리(edge)로 가지는 두 개의 반-평면(half-plane)의 합집합(union)으로 정의됩니다. 더 높은 차원에서, 이면체 각도는 두 개의 초평면(hyperplane) 사이의 각도를 나타냅니다.^[1] 날아가는 기계의 평면은 우현과 좌현 주 평면 둘 다가 옆쪽 축에 대해 위쪽으로 기울어질 때 양의 이면체 각도에 있다고 말합니다. 아래쪽으로 기울어질 때 그것들은 음의 이면체 각도에 있다고 말합니다.

Mathematical background

두 개의 교차하는 평면이 다음 두 방정식에 의해 데카르트 좌표(Cartesian coordinates)의 관점에서 설명될 때

a_{1}x+b_{1}y+c_{1}z+d_{1}=0

a_{2}x+b_{2}y+c_{2}z+d_{2}=0

그들 사이의 이면체 각도, $\varphi$ 는 다음에 의해 제공됩니다:

\cos \varphi ={\frac {\left\vert a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}\right\vert }{{\sqrt {a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}{\sqrt {a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}}}

그리고 $0\leq \varphi \leq \pi /2$ 을 만족시킵니다.

대안적으로, 만약 $n A$ 및 $n B$ 가 평면에 대한 법선 벡터(normal vector)이면, 우리는 다음을 가집니다:

\cos \varphi ={\frac {\left\vert \mathbf {n} _{\mathrm {A} }\cdot \mathbf {n} _{\mathrm {B} }\right\vert }{|\mathbf {n} _{\mathrm {A} }||\mathbf {n} _{\mathrm {B} }|}}

여기서 $n A \cdot n B$ 는 벡터의 점 곱(dot product)이고 $| n A | | n B |$ 는 그들 길이의 곱입니다.^[2]

절댓값은 위의 공식에서 요구되는데, 왜냐하면 평면은 하나의 방정식에서 모든 계수 부호를 변경할 때, 또는 하나의 법선 벡터를 그것의 반대로 대체될 때 변경되지 않기 때문입니다.

어쨌든, 절댓값은 그것의 경계가 같은 직선인 두 개의 절반 평면(half plane)의 이면체 각도를 고려할 때 피해질 수 있고 피해져야 합니다. 이 경우에서, 절반 평면은 그들의 교차의 점 $P$ , 및 $P + b 0$ , $P + b 1$ 및 $P + b 2$ 가 각각 교차 직선, 첫 번째 절반 평면, 및 두 번째 절반 평면에 속하는 것을 만족하는 세 벡터 $b 0$ , $b 1$ 및 $b 2$ 에 의해 설명될 수 있습니다. 이들 두 절반 평면의 이면체 각도는 다음에 의해 정의됩니다:

\cos \varphi ={\frac {(\mathbf {b} _{0}\times \mathbf {b} _{1})\cdot (\mathbf {b} _{0}\times \mathbf {b} _{2})}{|\mathbf {b} _{0}\times \mathbf {b} _{1}||\mathbf {b} _{0}\times \mathbf {b} _{2}|}}

,

그리고 $0\leq \varphi <\pi$ 를 만족시킵니다.

In polymer physics

고분자 물리(polymer physics)와 같은 일부 과학 분야에서, 우리는 점의 체인과 연속적인 점 사이의 연결을 고려할 수 있습니다. 만약 그 점들이 위치 $r 1$ , $r 2$ , $r 3$ , 등에서 순차적으로 번호가 매겨지고 위치되면, 결합 벡터는 보다 일반적으로, $u 1$ = $r 2$ - $r 1$ , $u 2$ = $r 3$ - $r 2$ , 및 $u i$ = $r i+1$ - $r i$ 에 의해 정의됩니다.^[3] 이것은 단백질 구조(protein structure)에서 운동학적 체인(kinematic chain) 또는 아미노산(amino acid)에 대한 경우입니다. 이들 경우에서, 우리는 종종 세 개의 연속된 점에 의해 정의된 평면과 두 개의 연속된 그러한 평면 사이의 이면체 각도에 관심이 있습니다. 만약 방향이 전체 체인에 대해 선택되면, 각 연속적인 점의 쌍은 벡터를 정의하고, 모든 이들 벡터 $u i$ 의 합은 체인의 시작으로부터 끝까지 가리키는 벡터입니다. 만약 $u 1$ , $u 2$ 및 $u 3$ 가 세 연속된 그러한 벡터이면, 우리는 평면의 교차점이 방향화된다는 것을 제외하고 앞의 경우와 유사한 상황을 가집니다. 이것은 구간 $(- π, π]$ 에 속하는 이면체 각도를 정의하는 것을 허용합니다. 이 이면체 각도는 다음에 의해 정의됩니다:^[4]

{\begin{aligned}\cos \varphi &={\frac {(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})}{|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}}\\\sin \varphi &={\frac {\mathbf {u} _{2}\cdot ((\mathbf {u} _{1}\times \mathbf {u} _{2})\times (\mathbf {u} _{2}\times \mathbf {u} _{3}))}{|\mathbf {u} _{2}|\,|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}},\end{aligned}}

또는, 함수 atan2를 사용하여 다음으로 정의됩니다:

\varphi =\operatorname {atan2} (\mathbf {u} _{2}\cdot ((\mathbf {u} _{1}\times \mathbf {u} _{2})\times (\mathbf {u} _{2}\times \mathbf {u} _{3})),|\mathbf {u} _{2}|\,(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})).

이 이면체 각도는 체인의 방향 (점이 고려되는 순서)에 의존하지 않습니다. 사실, 이 순서화를 변경하는 것은 각 벡터를 그것의 반대 벡터로 대체하고, 인덱스 1과 3을 교환하는 것으로 구성됩니다. 연산 둘 다는 코사인을 바꾸지 않고, 사인의 부호를 바꿉니다. 따라서, 함께, 그것들은 각도를 바꾸지 않습니다.

같은 이면체 각도에 대해 더 간단한 공식은 다음입니다 (증명은 아래에 주어집니다)

{\begin{aligned}\cos \varphi &={\frac {(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})}{|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}}\\\sin \varphi &={\frac {|\mathbf {u} _{2}|\,\mathbf {u} _{1}\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})}{|\mathbf {u} _{1}\times \mathbf {u} _{2}|\,|\mathbf {u} _{2}\times \mathbf {u} _{3}|}},\end{aligned}}

또는 동등하게,

\varphi =\operatorname {atan2} (|\mathbf {u} _{2}|\,\mathbf {u} _{1}\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3}),(\mathbf {u} _{1}\times \mathbf {u} _{2})\cdot (\mathbf {u} _{2}\times \mathbf {u} _{3})).

이것은 벡터 사중 곱(vector quadruple product) 공식을 사용함으로써 이전 공식과, 스칼라 삼중 곱(scalar triple product)이 만약 그것이 같은 벡터를 두 번 포함하면 영이라는 사실로부터 추론될 수 있습니다:

(\mathbf {u} _{1}\times \mathbf {u} _{2})\times (\mathbf {u} _{2}\times \mathbf {u} _{3})=[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{1}]\mathbf {u} _{2}-[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{2}]\mathbf {u} _{1}=[(\mathbf {u} _{2}\times \mathbf {u} _{3})\cdot \mathbf {u} _{1}]\mathbf {u} _{2}

특별한 경우는 $\varphi =\pi$ , $\varphi =+\pi /3$ 및 $\varphi =-\pi /3$ 이며, 이것은 trans, gauche⁺, 및 gauche⁻ 형태라고 불립니다.

In stereochemistry


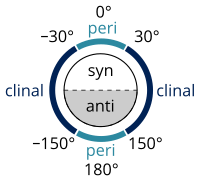
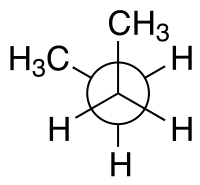
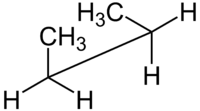
Configuration names according to dihedral angle	syn n-Butane Newman projection	syn n-Butane sawhorse projection

입체-화학(stereochemistry)에서 비틀림 각도(torsion angle)는 화학 결합(chemical bond)에 의해 연결된 분자의 두 부분의 기하학적 관계를 설명하는 이면체 각도의 특정 예제로 정의됩니다.^[5]^[6] 분자(molecule)의 같은 직선 위에 있지 않은 세 원자의 모든 각 집합은 하나의 평면을 정의합니다. 두 그러한 평면 (즉, 네 연속적으로-결합된 원자의 집합)이 교차할 때, 그들 사이의 각도는 이면체 각도입니다. 이면체 각도는 분자 형태(molecular conformation)를 지정하기 위해 사용됩니다.^[7] 0°과 ±90° 사이의 각도에 해당하는 입체-화학적(Stereochemical) 배열은 syn (s), ±90°와 180° 사이의 그것들은 anti (a) 해당합니다. 마찬가지로, 30°와 150° 또는 −30°와 −150° 사이의 각도에 해당하는 배열은 clinal (c)라고 불리고 0°과 ±30° 또는 ±150°와 180° 사이의 배열은 periplanar (p)라고 불립니다.

두 가지 유형의 용어는 네 가지 각도의 범위를 정의하기 위해 결합될 수 있습니다; 0°에서 ±30°는 synperiplanar (sp); 30°에서 90° 및 −30°에서 −90°는 synclinal (sc); 90°에서 150° 및 −90°에서 −150°는 anticlinal (ac); ±150°에서 180°은 antiperiplanar (ap)입니다. synperiplanar 형태는 syn- or cis-형태로; antiperiplanar는 anti 또는 trans로; 그리고 synclinal는 gauche 또는 skew로 역시 알려져 있습니다.

예를 들어, n-뷰테인(butane)을 갖는 두 평면은 두 중심 카본 원자와 메칠 카본 원자의 하나의 관점에서 지정될 수 있습니다. 갖는 위에서 보여준 60°의 이면체 각도를 syn-형태는 180°의 이면체 각도를 갖는 anti-형태보다 덜 안정적입니다.

거대-분자 사용법에 대해, 기호 T, C, G⁺, G⁻, A⁺ 및 A⁻는 (각각, ap, sp, +sc, −sc, +ac 및 −ac에 대해) 추천됩니다

Proteins

라마찬드런 플롯(Ramachandran plot)은 (역시 라마찬드런 다이어그램 또는 [φ,ψ] 플롯으로 알려져 있으며), 원래 G. N. Ramachandran, C. Ramakrishnan, 및 V. Sasisekharan에 의해 1963년에 개발되었으며,^[8] 단백질 구조(protein structure)에서 아미노산(amino acid) 잔여의 φ에 대한 백본 이면체 각도 ψ에 대해 에너지적으로 허용된 영역을 시각화하기 위한 방법입니다. 오른쪽에 그림은 (라마찬드런에 의해 φ와 φ′으로 불리는) φ와 ψ 백본 이면체 각도의 정의를 묘사합니다.^[9]

단백질(protein) 체인에서 세 개의 이면체 각도는 다이어그램에 표시된 것처럼 φ (파이), ψ (씨이) 및 ω (오메가)로 정의됩니다. 펩타이드 결합(peptide bond)의 평면성은 보통 ω를 180° (전형적인 trans 경우) 또는 0° (드문 cis 경우)로 제한합니다. trans 및 cis 이성질체(isomers)에서 C^α 원자 사이의 거리는 각각 대략적으로 3.8 및 2.9 Å입니다. 단백질에서 대부분의 펩타이드 결합은, 비록 단백질(proline)의 질소에 대한 펩타이드 결합이 다른 아미노산 쌍에 비해 cis의 증가된 널리-퍼짐을 가질지라도, trans입니다.^[10]

측면 연쇄 이면체 각도는 χ_n (chi-n)으로 지정됩니다.^[11] 그것들은 180°, 60°, 및 −60° 근처에서 군집하는 경향이 있으며, 이것은 trans, gauche⁺, 및 gauche⁻ 형태라고 불립니다. 특정 측면-연쇄 이면체 각도의 안정성은 값 φ 및 ψ에 의해 영향을 받습니다.^[12] 예를 들어, ψ가 −60°에 가까울 때 gauche⁺ 로더머(rotamer)에서 측면 연쇄의 Cγ와 다음 잔여의 백본 질소 사이에 직접적인 입체 상호-작용이 있습니다.^[13]

Converting from dihedral angles to Cartesian coordinates in chains

고분자 백본, 특히 단백질을, 내부 좌표(internal coordinates); 즉, 연속적인 이면체 각도와 결합 길이의 목록에서, 나타내는 것이 공통적입니다. 어쨌든, 일부 유형의 계산 화학(computational chemistry)은 대신에 데카르트 좌표(cartesian coordinates)를 사용합니다. 계산 구조 최적화에서, 일부 프로그램은 그들의 반복 동안 이들 표현 사이에 앞뒤로 빠르게 뒤집는 것이 필요합니다. 이 임무는 계산 시간을 지배할 수 있습니다. 많은 반복을 갖는 또는 긴 체인을 갖는 과정에 대해, 부정확한 누적 수치가 역시 도입될 수 있습니다. 모든 변환 알고리듬은 수치적으로 동등한 결과를 생성하지만, 그것들은 속도와 수치적 정확도에서 다릅니다.^[14]^{[non-primary source needed]}

Geometry

모든 각 다면체는 해당 가장자리를 공유하는 두 면의 관계를 설명하는 모든 각 가장자리에서 이면체 각도를 가집니다. 이 이면체 각도는, 역시 면 각도(face angle)라고 불리며, 다면체에 관한 내부 각도(internal angle)로 측정됩니다. 0°의 각도는 면 법선 벡터가 역평행(antiparallel)이고 그 면들이 서로 겹치는 것을 의미하며, 이것은 그것이 퇴화(degenerate) 다면체의 일부임을 의미합니다. 180°의 각도는 그 면들이, 타일링(tiling)에서 처럼, 평행함을 의미합니다. 180°보다 큰 각도가 다면체의 오목한 부분에 존재합니다.

가장자리-전이(edge-transitive) 다면체에서 모든 각 이면체 각도는 같은 값을 가집니다. 이것은 5 플라톤 고체(Platonic solid), 13 카탈랑 고체(Catalan solid), 4 케플러-푸앵소 다면체(Kepler–Poinsot polyhedra), 두 개의 준정규 고체, 및 두 개의 준정규 이중 고체를 포함합니다.

공통 꼭짓점 P에서 만나고 가장자리 AP, BP 및 CP를 갖는 다면체의 세 면이 주어지면, APC와 BPC를 포함하는 면 사이의 이면체 각도의 코사인은 다음입니다:^[15]

\cos \varphi ={\frac {\cos(\angle \mathrm {APB} )-\cos(\angle \mathrm {APC} )\cos(\angle \mathrm {BPC} )}{\sin(\angle \mathrm {APC} )\sin(\angle \mathrm {BPC} )}}

References

^ Olshevsky, George. "Dihedral angle". Glossary for Hyperspace. Archived from the original on 4 February 2007.
^ "Angle Between Two Planes". TutorVista.com. Retrieved 2018-07-06.
^ Kröger, Martin (2005). Models for polymeric and anisotropic liquids. Springer. ISBN 3540262105.
^ Blondel, Arnaud; Karplus, Martin (7 Dec 1998). "New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: Elimination of singularities". Journal of Computational Chemistry. 17 (9): 1132–1141. doi:10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T.
^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Torsion angle".
^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Dihedral angle".
^ Anslyn, Eric; Dennis Dougherty (2006). Modern Physical Organic Chemistry. University Science. p. 95. ISBN 978-1891389313.
^ Ramachandran, G. N.; Ramakrishnan, C.; Sasisekharan, V. (1963). "Stereochemistry of polypeptide chain configurations". Journal of Molecular Biology. 7: 95–9. doi:10.1016/S0022-2836(63)80023-6. PMID 13990617.
^ Richardson, J. S. (1981). Anatomy and Taxonomy of Protein Structures. Advances in Protein Chemistry. Vol. 34. pp. 167–339. doi:10.1016/S0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376.
^ Singh J, Hanson J, Heffernan R, Paliwal K, Yang Y, Zhou Y (August 2018). "Detecting Proline and Non-Proline Cis Isomers in Protein Structures from Sequences Using Deep Residual Ensemble Learning". Journal of Chemical Information and Modeling. 58 (9): 2033–2042. doi:10.1021/acs.jcim.8b00442. PMID 30118602.
^ http://www.cryst.bbk.ac.uk/PPS95/course/3_geometry/conform.html
^ Dunbrack, RL Jr.; Karplus, M (20 March 1993). "Backbone-dependent rotamer library for proteins. Application to side-chain prediction". Journal of Molecular Biology. 230 (2): 543–74. doi:10.1006/jmbi.1993.1170. PMID 8464064.
^ Dunbrack, RL Jr; Karplus, M (May 1994). "Conformational analysis of the backbone-dependent rotamer preferences of protein sidechains". Nature Structural Biology. 1 (5): 334–40. doi:10.1038/nsb0594-334. PMID 7664040.
^ Parsons, J.; Holmes, J. B.; Rojas, J. M.; Tsai, J.; Strauss, C. E. (2005), "Practical conversion from torsion space to cartesian space for in silico protein synthesis", Journal of Computational Chemistry, 26 (10): 1063–1068, doi:10.1002/jcc.20237, PMID 15898109
^ "dihedral angle calculator polyhedron". www.had2know.com. Archived from the original on 25 November 2015. Retrieved 25 October 2015.

External links

The Dihedral Angle in Woodworking at Tips.FM
Analysis of the 5 Regular Polyhedra gives a step-by-step derivation of these exact values.

[1] Olshevsky, George. "Dihedral angle". Glossary for Hyperspace. Archived from the original on 4 February 2007.

[2] "Angle Between Two Planes". TutorVista.com. Retrieved 2018-07-06.

[kroger-3] Kröger, Martin (2005). Models for polymeric and anisotropic liquids. Springer. ISBN 3540262105.

[4] Blondel, Arnaud; Karplus, Martin (7 Dec 1998). "New formulation for derivatives of torsion angles and improper torsion angles in molecular mechanics: Elimination of singularities". Journal of Computational Chemistry. 17 (9): 1132–1141. doi:10.1002/(SICI)1096-987X(19960715)17:9<1132::AID-JCC5>3.0.CO;2-T.

[5] IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Torsion angle".

[6] IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Dihedral angle".

[dougherty-7] Anslyn, Eric; Dennis Dougherty (2006). Modern Physical Organic Chemistry. University Science. p. 95. ISBN 978-1891389313.

[8] Ramachandran, G. N.; Ramakrishnan, C.; Sasisekharan, V. (1963). "Stereochemistry of polypeptide chain configurations". Journal of Molecular Biology. 7: 95–9. doi:10.1016/S0022-2836(63)80023-6. PMID 13990617.

[9] Richardson, J. S. (1981). Anatomy and Taxonomy of Protein Structures. Advances in Protein Chemistry. Vol. 34. pp. 167–339. doi:10.1016/S0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376.

[10] Singh J, Hanson J, Heffernan R, Paliwal K, Yang Y, Zhou Y (August 2018). "Detecting Proline and Non-Proline Cis Isomers in Protein Structures from Sequences Using Deep Residual Ensemble Learning". Journal of Chemical Information and Modeling. 58 (9): 2033–2042. doi:10.1021/acs.jcim.8b00442. PMID 30118602.

[11] ttp://www.cryst.bbk.ac.uk/PPS95/course/3_geometry/conform.html

[12] Dunbrack, RL Jr.; Karplus, M (20 March 1993). "Backbone-dependent rotamer library for proteins. Application to side-chain prediction". Journal of Molecular Biology. 230 (2): 543–74. doi:10.1006/jmbi.1993.1170. PMID 8464064.

[13] Dunbrack, RL Jr; Karplus, M (May 1994). "Conformational analysis of the backbone-dependent rotamer preferences of protein sidechains". Nature Structural Biology. 1 (5): 334–40. doi:10.1038/nsb0594-334. PMID 7664040.

[NERF-14] Parsons, J.; Holmes, J. B.; Rojas, J. M.; Tsai, J.; Strauss, C. E. (2005), "Practical conversion from torsion space to cartesian space for in silico protein synthesis", Journal of Computational Chemistry, 26 (10): 1063–1068, doi:10.1002/jcc.20237, PMID 15898109

[15] "dihedral angle calculator polyhedron". www.had2know.com. Archived from the original on 25 November 2015. Retrieved 25 October 2015.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]