Histogram

Original article: wikipedia:Histogram

For the histogram used in digital image processing, see Image histogram and Color histogram.

Histogram
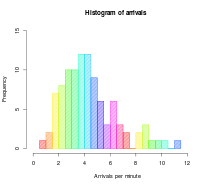One of the Seven Basic Tools of Quality
First described by	Karl Pearson
Purpose	To roughly assess the probability distribution of a given variable by depicting the frequencies of observations occurring in certain ranges of values.

히스토그램(histogram)은 수치 데이터의 분포(distribution)의 근사한 표현입니다. 그 용어는 칼 피어슨(Karl Pearson)에 의해 처음 소개되었습니다. 히스토그램을 구성하기 위해, 첫 번째 과정은 먼저 값의 범위를 "상자에 넣는(bin)" 것이고—즉, 일련의 구간으로 값의 전체 범위를 나누고—그런 다음 각 구간(interval)에 몇 개의 값이 들어갈지 셉니다. 그 상자는 보통 변수의 연속적이고, 겹치지 않는 구간으로 지정됩니다. 상자 (구간)은 인접되어야 하고 종종 같은 크기입니다 (그러나 필수적인 것은 아닙니다).

만약 상자가 같은 크기에 있으면, 막대기가 빈도수(frequency)—각 상자에서 경우의 숫자—에 비례하는 높이로 상자 위에 그려집니다. 히스토그램은 높이의 합이 1이 되도록 여러 카테고리(categories) 각각에 해당하는 경우의 비율을 보여주는 "상대적" 빈도를 표시하기 위해 정규화될 수도 있습니다.

어쨌든, 상자는 같은 너비일 필요는 없습니다; 그런 경우에서, 세워진 사각형은 상자에서 경우의 빈도수에 비례하는 그의 넓이(area)를 갖도록 정의됩니다. 수직 축은 그런-다음 빈도가 아니라 빈도 밀도(frequency density)—수평 축에서 변수의 단위당 경우의 숫자입니다. 변수 상자 너비의 예제는 아래의 인구 조사국 데이터에 표시되어 있습니다.

인접 상자가 틈이 없어야 하기 때문에, 히스토그램의 사각형은 원래 변수가 연속적임을 나타내기 위해 서로 접촉합니다.

히스토그램은 데이터의 놓이는 분포의 밀도에 대한 대략적인 의미를 제공하고, 종종 밀도 추정(density estimation)에 사용됩니다: 즉, 놓이는 변수의 확률 밀도 함수(probability density function)를 추정합니다. 확률 밀도에 사용되는 히스토그램의 전체 넓이는 항상 1로 정규화됩니다. 만약 x-축 구간 위의 길이가 모두 1이면, 히스토그램은 상대 빈도(relative frequency) 그림과 동일합니다.

히스토그램은 품질 관리의 7가지 기본 도구 중 하나입니다.

히스토그램은 때때로 막대 차트(bar charts)와 혼동됩니다. 히스토그램은 연속 데이터(continuous data)에 사용되며, 여기서 상자는 데이터 범위를 나타내고, 반면에 막대 차트(bar chart)는 카테고리적 변수(categorical variables)의 그림입니다. 일부 저자는 구별을 분명히 하기 위해 막대 차트는 사각형 사이에 틈을 가지는 것을 권장합니다.

막대 그래프와 히스토그램은 두 가지 공통적인 유형의 데이터 그래픽 표현입니다. 그것들은 비슷해 보일 수 있지만, 이해해야 할 중요한 둘 사이의 일부 주요 차이점이 있습니다.

막대 그래프는 막대를 사용하여 다양한 데이터 카테고리의 빈도 또는 수량을 나타내는 차트입니다. 막대는 수직 또는 수평일 수 있고, 그것들은 전형적으로 다른 카테고리를 쉽게 비교할 수 있도록 수평 또는 수직으로 정렬됩니다. 막대 그래프는 학교에서 다양한 학년 수준의 학생 수와 같이 개별 카테고리로 나눌 수 있는 데이터를 표시하는 데 유용합니다.

히스토그램은, 다른 한편으로, 수치 데이터의 분포를 보여주는 그래프입니다. 그것은 상자(Bin)라고 하는 다양한 숫자 범위 내에서 관찰의 빈도 또는 수를 표시하는 일종의 막대 차트입니다. 상자는 보통 변수의 연속적이고, 겹치지 않는 구간으로 지정됩니다. 히스토그램은 데이터 분포를 시각적으로 표현하여, 각 상자에 속하는 관측의 숫자를 보여줍니다. 이것은 데이터의 패턴과 추세를 식별하고, 서로 다른 데이터-집합 사이를 비교하는 데 유용할 수 있습니다.

Examples

다음은 500개 항목을 사용하는 오른쪽 히스토그램의 데이터입니다:

Bin/Interval	Count/Frequency
−3.5 to −2.51	9
−2.5 to −1.51	32
−1.5 to −0.51	109
−0.5 to 0.49	180
0.5 to 1.49	132
1.5 to 2.49	34
2.5 to 3.49	4

히스토그램의 패턴을 설명하기 위해 사용되는 단어는 "대칭", "왼쪽으로 치우침" 또는 "오른쪽", "단일-봉우리", "이중-봉우리" 또는 "다중-봉우리"입니다.

• 
  Symmetric, unimodal
• 
  Skewed right
• 
  Skewed left
• 
  Bimodal
• 
  Multimodal
• 
  Symmetric

데이터에 대해 자세히 알아보기 위해, 여러 상자 너비를 사용하여 데이터를 그리는 것이 좋습니다. 다음은 식당에서 주는 팁의 예입니다.

• 
  Tips using a $1 bin width, skewed right, unimodal
• 
  Tips using a 10c bin width, still skewed right, multimodal with modes at $ and 50c amounts, indicates rounding, also some outliers

미국 인구 조사국은 집 밖에서 일하는 사람이 1억 2,400만 명이라고 밝혔습니다. 출퇴근 시간에 대한 데이터를 사용하여 아래 테이블은 이동 시간이 "최소 30분 이상 35분 미만"이라고 응답한 사람들의 절대 수가 위 및 아래 카테고리의 숫자보다 높다는 것을 보여줍니다. 이것은 사람들이 보고된 이동 시간을 반올림했기 때문일 수 있습니다. 값을 임의로 반올림한 숫자로 보고하는 문제는 사람들로부터 데이터를 수집할 때 흔히 발생하는 현상입니다.

Histogram of travel time (to work), US 2000 census. Area under the curve equals the total number of cases. This diagram uses Q/width from the table.

Data by absolute numbers

Interval	Width	Quantity	Quantity/width
0	5	4180	836
5	5	13687	2737
10	5	18618	3723
15	5	19634	3926
20	5	17981	3596
25	5	7190	1438
30	5	16369	3273
35	5	3212	642
40	5	4122	824
45	15	9200	613
60	30	6461	215
90	60	3435	57

이 히스토그램은 각 블록의 넓이가 해당 카테고리에 해당하는 조사 대상자의 수와 같아지도록 단위 구간당 사례 수를 각 블록의 높이로 표시합니다. 곡선 아래 넓이는 총 사례 수 (1억 2,400만 건)를 나타냅니다. 이 유형의 히스토그램은 절대 숫자를 표시하며, Q는 천 단위입니다.

Histogram of travel time (to work), US 2000 census. Area under the curve equals 1. This diagram uses Q/total/width from the table.

Data by proportion

Interval	Width	Quantity (Q)	Q/total/width
0	5	4180	0.0067
5	5	13687	0.0221
10	5	18618	0.0300
15	5	19634	0.0316
20	5	17981	0.0290
25	5	7190	0.0116
30	5	16369	0.0264
35	5	3212	0.0052
40	5	4122	0.0066
45	15	9200	0.0049
60	30	6461	0.0017
90	60	3435	0.0005

이 히스토그램은 수직 스케일에서만 첫 번째 히스토그램과 다릅니다. 각 블록의 넓이는 각 카테고리가 나타내는 총 넓이의 일부이고, 모든 막대의 총 넓이는 1 ("모두"를 의미하는 분수)과 같습니다. 표시된 곡선은 단순한 밀도 추정(density estimate)입니다. 이 버전은 비율을 표시하고, 단위 넓이 히스토그램이라고도 합니다.

다시 말해서, 히스토그램은 너비가 클래스 구간을 나타내고 넓이가 해당 빈도에 비례하는 직사각형을 통해 빈도 분포를 나타냅니다: 각각의 높이는 구간의 평균 빈도 밀도입니다. 구간은 히스토그램으로 표시되는 데이터가 배타적이지만 연속적임을 보여주기 위해 함께 배치됩니다. (예를 들어, 히스토그램에서 10.5–20.5 및 20.5–33.5의 두 연결 구간을 가질 수 있지만, 10.5–20.5 및 22.5–32.5의 두 연결 구간은 불가능합니다. 빈 구간은 비어 있는 것으로 표시되고 건너뛰지 않습니다.)

Mathematical definitions

An ordinary and a cumulative histogram of the same data. The data shown is a random sample of 10,000 points from a normal distribution with a mean of 0 and a standard deviation of 1.

히스토그램을 구성하기 위해 사용되는 데이터는 각각의 서로소 카테고리 (상자(bins)라고 알려져 있음)에 속하는 관측의 숫자를 세는 m_i 함수를 통해 생성됩니다. 따라서, 우리가 n을 관측의 총 개수라고 놓고 k를 총 상자의 개수로 지정하면, 히스토그램 데이터 m_i는 다음 조건을 충족합니다:

$n=\sum _{i=1}^{k}{m_{i}}.$

히스토그램은 커널을 사용하여 상자에 걸쳐 빈도를 매끄럽게 하는 단순한 커널 밀도 추정(kernel density estimation)으로 생각될 수 있습니다. 이것은 일반적으로 놓여있는 변수의 분포를 더 정확하게 반영하는 더 매끄러운 확률 밀도 함수를 산출합니다. 밀도 추정은 히스토그램의 대안으로 표시될 수 있고, 보통 상자의 집합이 아닌 곡선으로 그려집니다. 그럼에도 불구하고 히스토그램은 그것들의 통계적 특성을 모델링해야 하는 응용에서 선호됩니다. 커널 밀도 추정의 상관 변동은 수학적으로 설명하기가 매우 어려운 반면 각 상자가 독립적으로 변하는 히스토그램의 경우 간단합니다.

커널 밀도 추정의 대안은 계산이 빠르고 커널을 사용하지 않고 밀도의 매끄러운 곡선 추정을 제공하는 이동된 평균 히스토그램입니다.

Cumulative histogram

누적 히스토그램은 모든 상자에서 지정된 상자까지의 누적 관측의 숫자를 세는 매핑입니다. 즉, 히스토그램 m_j의 누적 히스토그램 M_i는 다음과 같이 정의됩니다:

$M_{i}=\sum _{j=1}^{i}{m_{j}}.$

Number of bins and width

상자의 "최적" 개수는 없고, 다른 상자 크기는 데이터의 다양한 특징을 드러날 수 있습니다. 그룹화 데이터는 적어도 17세기 그란트(Graunt)의 연구만큼 오래되었지만, 1926년 스터지스(Sturges)의 연구까지 시스템적인 지침이 제공되지 않았습니다.

놓여있는 데이터 점의 밀도가 낮은 더 넓은 상자를 사용하는 것은 표본화 무작위성으로 인한 노이즈를 줄입니다; 밀도가 높은 (그래서 신호가 노이즈를 제거함) 더 좁은 상자를 사용하는 것은 밀도 추정에 더 큰 정밀도를 제공합니다. 따라서 히스토그램 내에서 상자-너비를 변경하는 것은 도움이 될 수 있습니다. 그럼에도 불구하고, 너비가 같은 상자가 널리 사용됩니다.

일부 이론가는 최적의 상자의 수를 결정하려고 시도했지만, 이들 방법은 일반적으로 분포의 모양에 대해 강력한 가정을 합니다. 실제 데이터 분포와 분석 목표에 따라, 다른 상자 너비가 적절할 수 있으므로, 보통 적절한 너비를 결정하기 위해 실험이 필요합니다. 어쨌든, 다양한 유용한 지침과 경험 법칙이 있습니다.

상자의 숫자 k는 직접 할당되거나 제안된 상자 너비 h에서 다음과 같이 계산될 수 있습니다:

$k=\left\lceil {\frac {\max x-\min x}{h}}\right\rceil .$

괄호는 천장 함수(ceiling function)를 나타냅니다.

Square-root choice

$k=\lceil {\sqrt {n}}\rceil \,$

이는 표본 (Excel의 Analysis Toolpak 히스토그램과 기타 여러 항목에서 사용됨)에서 데이터 점의 개수의 제곱근을 취하고 다음 정수로 반올림합니다.

Sturges' formula

Sturges의 공식은 이항 분포(binomial distribution)에서 유도되고 근사적으로 정규 분포를 암묵적으로 가정합니다.

$k=\lceil \log _{2}n\rceil +1,\,$

Sturges의 공식은 암묵적으로 데이터 범위에 기반한 상자 크기이고, n < 30이면 성능이 저하될 수 있는데, 왜냐하면 상자의 개수가 7개 미만으로 적고 데이터에서 추세를 제대로 표시할 가능성이 없기 때문입니다. 다른 극단적인 경우, Sturges의 공식은 매우 큰 데이터집합에 대해 상자 너비를 과대 평가하여, 과도하게 매끄러운 히스토그램을 생성할 수 있습니다. 데이터가 정규적으로 분포되지 않으면 성능이 저하될 수도 있습니다.

Scott의 규칙 및 Terrell-Scott 규칙, 히스토그램 상자에 대해 널리 인정되는 다른 두 공식과 비교할 때, Sturges의 공식 출력은 n ≈ 100일 때 가장 가깝습니다.

Rice rule

$k=\lceil 2{\sqrt[{3}]{n}}\rceil ,$

Rice 규칙은 Sturges의 규칙에 대한 간단한 대안으로 제시됩니다.

Doane's formula

Doane의 공식은 비-정규 데이터로 성능을 향상시키려고 시도하는 Sturges의 공식을 수정한 것입니다.

$k=1+\log _{2}(n)+\log _{2}\left(1+{\frac {|g_{1}|}{\sigma _{g_{1}}}}\right)$

여기서 $g_{1}$는 추정된 분포의 3차-모멘트-기울어짐이고 다음과 같습니다:

$\sigma _{g_{1}}={\sqrt {\frac {6(n-2)}{(n+1)(n+3)}}}$

Scott's normal reference rule

상자 너비 $h$는 다음에 의해 제공됩니다:

$h={\frac {3.49{\hat {\sigma }}}{\sqrt[{3}]{n}}},$

여기서 ${\hat {\sigma }}$는 표본 표준 편차(standard deviation)입니다. Scott의 정규 참조 규칙은 밀도 추정의 적분 평균 제곱 오차를 최소화한다는 점에서 정규 분포 데이터의 무작위 표본에 최적입니다.

Freedman–Diaconis' choice

프리드먼-디콘 규칙(Freedman–Diaconis rule)은 상자 너비 $h$를 다음과 같이 제공합니다:

$h=2{\frac {\operatorname {IQR} (x)}{\sqrt[{3}]{n}}},$

이는 IQR로 표시되는 사분위수-사이 범위(interquartile range)를 기반으로 합니다. 그것은 Scott의 규칙의 3.5σ를 데이터에서 이상값에 대한 표준 편차보다 덜 민감한 2 IQR로 대체합니다.

Minimizing cross-validation estimated squared error

Scott의 규칙에서 적분된 평균 제곱 오차를 최소화하는 이 접근 방식은 leave-one out 교차 검증을 사용함으로써 정규 분포 이상으로 일반화될 수 있습니다:

${\underset {h}{\operatorname {arg\,min} }}{\hat {J}}(h)={\underset {h}{\operatorname {arg\,min} }}\left({\frac {2}{(n-1)h}}-{\frac {n+1}{n^{2}(n-1)h}}\sum _{k}N_{k}^{2}\right)$

여기서, $N_{k}$는 k-번째 상자의 데이터 점 개수이고, J를 최소화하는 h 값을 선택하면 적분된 평균 제곱 오차가 최소화됩니다.

Shimazaki and Shinomoto's choice

선택은 추정된 L² 위험 함수(risk function)의 최소화를 기반으로 합니다:

${\underset {h}{\operatorname {arg\,min} }}{\frac {2{\bar {m}}-v}{h^{2}}}$

여기서 $\textstyle {\bar {m}}$과 $\textstyle v$는 상자-너비 $\textstyle h$, $\textstyle {\bar {m}}={\frac {1}{k}}\sum _{i=1}^{k}m_{i}$, 및 $\textstyle v={\frac {1}{k}}\sum _{i=1}^{k}(m_{i}-{\bar {m}})^{2}$를 갖는 히스토그램의 평균과 편향된 분산입니다.

Variable bin widths

구간이 균등한 상자를 선택하는 것이 아닌, 일부 응용에 대해 상자 너비를 변경하는 것이 좋습니다. 이렇게 하면 카운트가 낮은 상자를 피할 수 있습니다. 공통적인 경우는 각 상자의 표본 수가 거의 같을 것으로 예상되는 동등-확률 상자(equiprobable bins)를 선택하는 것입니다. 상자는 일부 알려진 분포에 따라 선택되거나 각 상자가 $\approx n/k$ 표본을 가지도록 데이터를 기반으로 선택될 수 있습니다. 히스토그램을 그릴 때, 종속 축에 대해 빈도 밀도(frequency density)가 사용됩니다. 모든 상자가 근사적으로 같은 넓이를 가지지만, 히스토그램의 높이는 밀도 분포에 접근합니다.

동등-확률 상자에 대해, 상자의 숫자에 대해 다음과 같은 규칙이 제안됩니다:

$k=2n^{2/5}$

이러한 상자의 선택은 상자에 같은 숫자의 표본이 포함되어 있는지 여부를 테스트하는 피어슨 카이-제곱 테스트(Pearson chi-squared test)의 검정력을 최대화함으로써 동기가 부여됩니다. 보다 구체적으로, 주어진 신뢰 구간 $\alpha$에 대해 다음 방정식의 1/2과 1배 사이에서 선택하는 것이 좋습니다:

$k=4\left({\frac {2n^{2}}{\Phi ^{-1}(\alpha )}}\right)^{\frac {1}{5}}$

여기서 $\Phi ^{-1}$은 프로빗(probit) 함수입니다. $\alpha =0.05$에 대한 이 규칙을 따르면 $1.88n^{2/5}$와 $3.77n^{2/5}$ 사이를 제공합니다; 계수 2는 이 광범위한 최적에서 기억하기 쉬운 값으로 선택됩니다.

Remark

상자의 수가 ${\sqrt[{3}]{n}}$에 비례해야 하는 좋은 이유는 다음과 같습니다: 데이터가 매끄러운 밀도를 갖는 경계진 확률 분포의 $n$개의 독립적 실현으로 얻어진다고 가정합니다. 그런-다음 $n$이 무한대가 가는 경향이 있을 때 히스토그램은 똑같이 "울퉁불퉁한(rugged)" 것을 유지합니다. 만약 $s$가 분포의 "너비" (예를 들어, 표준 편차 또는 사분위수-사이 범위)이면 상자 (빈도)의 단위 수는 $nh/s$ 차수이고 상대 표준 오차는 ${\sqrt {s/(nh)}}$ 차수입니다. 다음 상자와 비교될 때, 빈도의 상대적 변화는 밀도의 도함수가 비-영이라는 조건으로 하여 $h/s$ 차수입니다. 이들 둘은 $k$가 ${\sqrt[{3}]{n}}$ 차수가 되도록 $h$가 $s/{\sqrt[{3}]{n}}$ 차수이면 같은 차수입니다. 이러한 간단한 세제곱근 선택은 역시 너비가 일정하지 않은 상자에도 적용될 수 있습니다.

Histogram and density function for a Gumbel distribution

Applications

• 수 문학(hydrology)에서 확률 분포(probability distribution)로 분석된 강우 및 하천 유출 데이터의 히스토그램 및 추정된 밀도 함수(density function)는 행동과 발생 빈도에 대한 통찰력을 얻는 데 사용됩니다. 파란색 그림에 예가 나와 있습니다.
• 많은 디지털 이미지 처리 프로그램에서, 픽셀의 대비 / 밝기 분포를 보여주는 히스토그램 도구가 있습니다.

  

  histogram of contrast

See also

• Data and information visualization
• Data binning
• Density estimation
  • Kernel density estimation, a smoother but more complex method of density estimation
• Entropy estimation
• Freedman–Diaconis rule
• Image histogram
• Pareto chart
• Seven basic tools of quality
• V-optimal histograms

Further reading

• Lancaster, H.O. An Introduction to Medical Statistics. John Wiley and Sons. 1974. ISBN 0-471-51250-8

External links

• Exploring Histograms, an essay by Aran Lunzer and Amelia McNamara
• Journey To Work and Place Of Work (location of census document cited in example)
• Smooth histogram for signals and images from a few samples
• Histograms: Construction, Analysis and Understanding with external links and an application to particle Physics.
• A Method for Selecting the Bin Size of a Histogram
• Histograms: Theory and Practice, some great illustrations of some of the Bin Width concepts derived above.
• Histograms the Right Way
• Interactive histogram generator
• Matlab function to plot nice histograms
• Dynamic Histogram in MS Excel
• Histogram construction and manipulation using Java applets, and charts on SOCR
• Toolbox for constructing the best histograms