Incenter

Original article: w:Incenter

The point of intersection of angle bisectors of the 3 angles of triangle ABC is the incenter (denoted by I). The incircle (whose center is I) touches each side of the triangle.

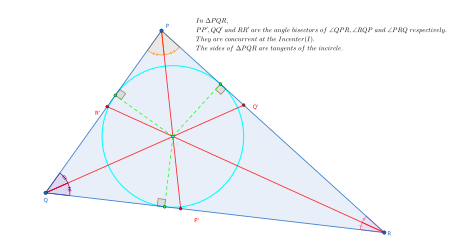
기하학(geometry)에서, 삼각형의 내중심(incenter)은 삼각형 중심(triangle center), 삼각형의 배치 또는 스케일과 무관한 방법으로 임의의 삼각형에 대해 정의된 점입니다. 내중심은 삼각형의 내부 각도 이등분선(angle bisector)이 교차하는 점으로, 삼각형의 변에서 등거리(equidistant)에 있는 점으로, 삼각형의 그래스파이어 변환(grassfire transform)의 중앙 축(medial axis)과 가장 안쪽 점의 접합점으로, 및 삼각형의 내접된 원(inscribed circle)의 중앙 점으로 동등하게 정의할 수 있습니다.

도형중심(centroid), 둘레중심(circumcenter), 및 직교중심(orthocenter)과 함께, 그것은 고대 그리스인에게 알려진 네 개의 삼각형 중심 중 하나이고, 일반적으로 오일러 직선(Euler line) 위에 놓이지 않은 유일한 것입니다. 그것은 클락 킴벌링(Clark Kimberling)의 삼각형 중심 백과사전(Encyclopedia of Triangle Centers)에 처음으로 나열된 중심, X(1)이고, 삼각형 중심의 곱셈 그룹(multiplicative group)의 항등 원소(identity element)입니다.

셋보다 많은 변을 갖는 다각형(polygon)에 대해, 내중심은 오직 접하는 다각형(tangential polygon) – 다각형의 각 변에 접하는(tangent) 내원을 가지는 다각형에 대해 존재합니다. 이 경우에서 내중심은 이 원의 중심이고 모든 변에서 같은 거리에 있습니다.

Definition and construction

삼각형의 세 내부 각도 이등분선(angle bisector)이 단일 점에서 만나는 것은 유클리드 기하학(Euclidean geometry)에서 하나의 정리(theorem)입니다. 유클리드(Euclid)의 원론(Elements)에서, 제 4권의 제안 4는 이 점이 역시 삼각형의 내접된 원의 중심임을 증명합니다. 내원 자체는 내중심에서 삼각형의 변 중 하나로 수직을 떨어뜨리고 해당 선분을 반지름으로 갖는 원을 그림으로써 구성될 수 있습니다.

내중심은 삼각형의 변을 형성하는 세 개의 선분과 그것들 선분을 포함하는 세 개의 직선으로부터 같은 거리에 놓입니다. 그것은 그 선분으로부터 같은 거리에 있는 유일한 점이지만, 주어진 삼각형의 외원(excircles)의 중심을 형성하는 외중심인 직선으로부터 같게 떨어져 있는 세 개의 점이 더 있습니다. 내중심과 외중심은 함께 직교중심 시스템(orthocentric system)을 형성합니다.

다각형의 중앙 축(medial axis)은 다각형에서 가장 가까운 이웃이 고유하지 않은 점의 집합입니다: 이들 점은 다각형의 둘 이상의 변에서 등거리에 있습니다. 중앙 축을 계산하는 한 가지 방법은 각각 다각형에서 일부 고정된 거리에 있는 오프셋 곡선(offset curves)의 연속 수열을 형성하는 그래스파이어 변환(grassfire transform)을 사용하는 것입니다; 중앙 축은 이들 곡선의 꼭짓점에 의해 추적됩니다. 삼각형의 경우에서, 중앙 축은 삼각형의 꼭짓점을 가장 안쪽 오프셋 곡선의 고유한 점인 내중심에 연결하는 각도 이등분선의 세 선분으로 구성됩니다. 다른 유형의 오프셋 곡선에서 유사한 방법으로 정의된 직선 뼈대(straight skeleton)는 볼록 다각형에 대해 중앙 축과 일치하고 따라서 역시 내중심에서 접합 점을 가집니다.

Proofs

Ratio proof

$\angle {BAC}$의 이등분선과 ${\overline {BC}}$가 $D$에서 만나고, $\angle {ABC}$의 이등분선과 ${\overline {AC}}$가 $E$에서 만나고, ${\overline {AD}}$와 ${\overline {BE}}$가 ${I}$에서 만난다고 놓습니다.

그리고 ${\overline {CI}}$과 ${\overline {AB}}$가 ${F}$에서 만난다고 놓습니다.

그런-다음 우리는 ${\overline {CI}}$가 $\angle {ACB}$의 이등분선임을 입증해야 합니다.

$\triangle {ACF}$에서, ${\overline {AC}}:{\overline {AF}}={\overline {CI}}:{\overline {IF}}$.

$\triangle {BCF}$에서, ${\overline {BC}}:{\overline {BF}}={\overline {CI}}:{\overline {IF}}$.

그러므로, ${\overline {AC}}:{\overline {AF}}={\overline {BC}}:{\overline {BF}}$이므로, ${\overline {AC}}:{\overline {BC}}={\overline {AF}}:{\overline {BF}}$입니다.

따라서 ${\overline {CF}}$는 $\angle {ACB}$의 이등분선입니다.

Perpendicular proof

각도 이등분선인 직선은 수직선에 의해 측정할 때 두 직선에서 등거리에 있습니다. 두 개의 이등분선이 교차하는 점에서, 이 점은 직선을 형성하는 최종 각도에서 수직적으로 등거리에 있고 (그것들이 이 각도 반대쪽 가장자리에서 같은 거리이기 때문임), 따라서 그것의 각도 이등분선 위에 놓입니다.

Relation to triangle sides and vertices

Trilinear coordinates

삼각형에서 한 점에 대해 삼선형 좌표(trilinear coordinates)는 삼각형 변에 대한 거리의 비율을 제공합니다. 내중심에 대해 삼선형 좌표는 다음에 의해 제공됩니다:

$\ 1:1:1.$

삼각형 중심의 모음은 삼선형 좌표의 좌표별 곱셈 아래에서 그룹(group)의 구조를 제공할 수 있습니다; 이 그룹에서, 내중심은 항등 원소(identity element)를 형성합니다.

Barycentric coordinates

삼각형의 한 점에 대한 질량중심 좌표(barycentric coordinates)는 그 점이 삼각형 꼭짓점 위치의 가중 평균임을 만족하는 가중치를 부여합니다. 내중심에 대해 질량중심 좌표는 다음에 의해 제공됩니다:

$\ a:b:c$

여기서 $a$, $b$, 및 $c$는 삼각형의 변의 길이이며, 또는 동등하게 (사인의 법칙(law of sines)을 사용하여) 다음에 의해 제공됩니다:

$\sin(A):\sin(B):\sin(C)$

여기서 $A$, $B$, 및 $C$는 세 꼭짓점에서 각도입니다.

Cartesian coordinates

내중심의 데카르트 좌표(Cartesian coordinates)는 둘레에 상대적인 삼각형의 변 길이를 가중으로 사용하여–즉, 합해서 단위가 되도록 정규화된 위에 주어진 질량-중심 좌표를 가중으로 사용하여–세 꼭짓점의 좌표의 가중 평균입니다. (가중은 양수이므로 내중심은 위에 설명된 것처럼 삼각형 내부에 놓입니다.) 만약 세 꼭짓점이 $(x_{A},y_{A})$, $(x_{B},y_{B})$, 및 $(x_{C},y_{C})$에 위치되고, 이들 꼭짓점 반대편 변이 대응하는 길이 $a$, $b$, 및 $c$를 가지면, 내중심은 다음에 있습니다:

${\bigg (}{\frac {ax_{A}+bx_{B}+cx_{C}}{a+b+c}},{\frac {ay_{A}+by_{B}+cy_{C}}{a+b+c}}{\bigg )}={\frac {a(x_{A},y_{A})+b(x_{B},y_{B})+c(x_{C},y_{C})}{a+b+c}}.$

Distances to vertices

삼각형 ABC의 내중심을 I로 표시하면, 내중심에서 꼭짓점까지의 거리는 삼각형 변의 길이와 결합하여 방정식을 따릅니다:

${\frac {IA\cdot IA}{CA\cdot AB}}+{\frac {IB\cdot IB}{AB\cdot BC}}+{\frac {IC\cdot IC}{BC\cdot CA}}=1.$

추가적으로,

$IA\cdot IB\cdot IC=4Rr^{2},$

여기서 R과 r은 삼각형의 각각 둘레반지름(circumradius)과 내반지름(circumradius)입니다.

Related constructions

Other centers

내중심에서 도형중심(centroid)까지의 거리는 삼각형의 가장 긴 중앙선(median) 길이의 삼분의 일보다 작습니다.

기하학에서 오일러의 정리(Euler's theorem in geometry)에 의해, 내중심 I에서 둘레중심 O까지의 제곱 거리는 다음에 의해 제공됩니다:

$OI^{2}=R(R-2r),$

여기서 R과 r은 각각 둘레반지름과 내반지름입니다; 따라서 둘레반지름은 적어도 내반지름의 두 배이며, 상등은 오직 등변(equilateral)인 경우입니다.

내중심에서 아홉 점 원(nine point circle)의 중심 N까지의 거리는 다음입니다:

$IN={\frac {1}{2}}(R-2r)<{\frac {1}{2}}R.$

내중심에서 직교중심(orthocenter) H까지의 제곱된 거리는 다음입니다:

$IH^{2}=2r^{2}-4R^{2}\cos A\cos B\cos C.$

부등식이 포함합니다:

$IG<HG,\quad IH<HG,\quad IG<IO,\quad 2IN<IO.$

내중심은 중점 삼각형(medial triangle) (그것의 꼭짓점이 변의 중간점인 삼각형)의 나겔 점(Nagel point)이고 따라서 이 삼각형 내부에 놓입니다. 반대로 임의의 삼각형의 나겔 점은 그것의 역보완 삼각형(anticomplementary triangle)의 내중심입니다.

내중심은 그것의 지름이 도형중심 G와 직교중심(orthocenter) H를 연결하는 디스크(disk) (직교-도형중심 디스크(orthocentroidal disk))의 내부에 놓여야 하지만, 그것은 아홉-점 중심(nine-point center)과 일치할 수 없으며, 그것의 위치가 지름을 따른 방향에서 (G에 더 가까운) 1/4에 고정됩니다. 직교-도형중심 디스크 내의 임의의 다른 점은 고유한 삼각형의 내중심입니다.

Euler line

삼각형의 오일러 직선(Euler line)은 다른 점 중에서 둘레중심(circumcenter), 도형중심(centroid), 및 직교중심(orthocenter)을 통과하는 직선입니다. 내중심은 일반적으로 오일러 직선 위에 놓이지 않습니다; 그것은 이등변 삼각형(isosceles triangle)에 대해 오직 오일러 직선 위에 있으며, 이것에 대해 오일러 직선이 삼각형의 대칭 축과 일치하고 모든 삼각형 중심을 포함합니다.

내중심에서 오일러 직선까지의 거리를 d, 가장 긴 중앙선의 길이를 v, 가장 긴 변의 길이를 u, 둘레반지름을 R, 직교중심에서 둘레중심까지의 오일러 선분의 길이를 e, 및 반둘레를 s로 표시하면, 다음 부등식이 유지됩니다:

${\frac {d}{s}}<{\frac {d}{u}}<{\frac {d}{v}}<{\frac {1}{3}};$

$d<{\frac {1}{3}}e;$

$d<{\frac {1}{2}}R.$

Area and perimeter splitters

삼각형의 넓이와 둘레를 절반으로 나누는 삼각형을 통과하는 임의의 직선은 삼각형의 내중심을 통과합니다; 넓이를 절반으로 나누는 내중심을 통과하는 모든 각 직선은 역시 둘레를 절반으로 나눕니다. 임의의 주어진 삼각형에 대해 이들 직선 중 하나, 둘, 또는 셋이 있습니다.

Relative distances from an angle bisector

X를 A의 내부 각도 이등분선 위에 있는 변하는 점이라고 놓습니다. 그런-다음 X = I (내중심)은 해당 각도 이등분선을 따라 비율 ${\tfrac {BX}{CX}}$를 최대화하거나 최소화합니다.

External links

• Weisstein, Eric W. "Incenter". MathWorld.