Disk (mathematics)

Disk with circumference (C) in black, diameter (D) in cyan, radius (R) in red, and center (O) in green.

기하학(geometry)에서, 디스크(disk, 역시 다른 철자(spelled)의 disc)^[1]는 원(circle)에 의해 경계진 평면(plane) 내의 영역입니다. 디스크는 만약 그것이 그것의 경계를 구성하는 원을 포함하면 닫은(closed), 그렇지 않으면 열린(open) 것이라고 말합니다.^[2]

Formulas

데카르트 좌표(Cartesian coordinates)에서, 중심 $(a,b)$ 와 반지름 R의 열린 디스크는 다음 공식에 의해 제공됩니다:^[1]

D=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}<R^{2}\}

반면에 같은 중심과 반지름의 닫힌 디스크는 다음에 의해 제공됩니다:

{\overline {D}}=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}\leq R^{2}\}.

반지름 R의 닫힌 또는 열린 디스크의 넓이(area)는 πR²입니다 (디스크의 넓이(area of a disk)를 참조하십시오).^[3]

Properties

디스크는 원형 대칭(circular symmetry)을 가집니다.^[4]

열린 원반과 닫힌 원반은 그것들이 서로에서 다른 토폴로지적 속성을 가지기 때문에 토폴로지적으로 동등하지 않습니다 (즉, 그것들이 위상동형(homeomorphic)이 아닙니다). 예를 들어, 모든 각 닫힌 디스크는 컴팩트(compact)이지만 모든 각 열린 디스크는 컴팩트이지 않습니다.^[5] 어쨌든, 대수적 토폴로지(algebraic topology)의 관점에서, 그것들은 많은 속성을 공유합니다: 그것들 둘 다는 수축-가능(contractible)이고^[6] 따라서 단일 점과 동등한 호모토피(homotopy equivalent)입니다. 이것은 그것들의 기본 그룹(fundamental group)이 자명한 것이고, 모든 호모롤지 그룹(homology group)이 Z와 동형인 0번째 그룹을 제외하고는 자명한 것임을 의미합니다. 점의 오일러 특성(Euler characteristic) (및 따라서 닫힌 디스크 또는 열린 디스크의 특성)은 1입니다.^[7]

닫힌 디스크에서 자체로의 모든 각 연속 맵(continuous map)은 적어도 하나의 고정된 점(fixed point)을 가집니다 (우리는 맵을 전단사(bijective) 또는 심지어 전사(surjective)이도록 요구하지 않습니다); 이것은 브라우어르 고정된 점 정리(Brouwer fixed point theorem)의 경우 n=2입니다.^[8] 그 명제는 열린 디스크에 대해 거짓입니다:^[9]

예를 들어 다음 함수를 생각해 보십시오:

f(x,y)=\left({\frac {x+{\sqrt {1-y^{2}}}}{2}},y\right)

이것은 열린 단위 디스크의 모든 각 점을 주어진 것의 오른쪽에 있는 열린 단위 디스크의 또 다른 점으로 매핑합니다. 그러나 닫힌 단위 디스크에 대해, 그것은 반원 $x^{2}+y^{2}=1,x>0$ 위에 모든 각 점을 고정합니다.

As a statistical distribution

The average distance to a location from points on a disc

단위 순환 디스크 위에 균등 분포는 통계학에서 때때로 마주칩니다. 그것은 도시 계획의 수학에서 운영 연구에서 가장 공통적으로 발생하며, 여기서 그것은 도시 내 인구를 모델링하기 위해 사용될 수 있습니다. 다른 용도는 주어진 선형 부등식의 집합이 만족시킬 확률을 계산하기 쉬운 분포라는 사실의 이점을 이용할 수 있습니다. (이것은 평면에서 가우스 분포(Gaussian distributions)에 대해 수치적 구적법(numerical quadrature)을 요구합니다.)

"기본 함수를 통한 독창적인 논증"은 디스크에서 두 점 사이의 평균 유클리드 거리(Euclidean distance)가 $128 / 45π \approx 0.90541$ 임을 보여주고,^[10] 반면에 극 좌표에서 직접 적분은 평균 제곱 거리가 $1$ 임을 보여줍니다.

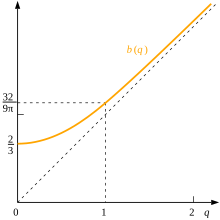
만약 우리가 디스크의 중심에서 거리 $q$ 에 임의적인 위치가 주어지면, 역시 분포에서 점에서 이 위치까지의 평균 거리 $b (q)$ 와 그러한 거리의 평균 제곱을 결정하는 것이 흥미롭습니다. 후자의 값은 $q 2 + 1 / 2$ 로 직접 계산될 수 있습니다.

Average distance to an arbitrary internal point

The average distance from a disk to an internal point

$b (q)$ 를 찾기 위해, 우리는 그 위치가 내부 또는 외부인지, 즉 $q ≶ 1$ 인 경우를 별도로 살펴볼 필요가 있고, 우리는 두 경우 모두에서 결과가 오직 완전한 타원 적분(complete elliptic integrals)의 관점에서 표현될 수 있음을 발견했습니다.

만약 우리가 내부 위치를 고려하면, 우리의 목표 (다이어그램을 참조)는 그것의 밀도가 $0 \leq r \leq s (θ)$ 에 대해 $1 / π$ 인 분포 아래에서 $r$ 의 기댓값을 계산하고, 셀의 넓이가 $r d r dθ$ 인 고정된 위치에 중심을 둔 극 좌표에서 적분합니다; 따라서 $b(q)={\frac {1}{\pi }}\int _{0}^{2\pi }{\textrm {d}}\theta \int _{0}^{s(\theta )}r^{2}{\textrm {d}}r={\frac {1}{3\pi }}\int _{0}^{2\pi }s(\theta )^{3}{\textrm {d}}\theta .$

여기서 $s (θ)$ 는 코사인의 법칙(Law of cosines)을 사용하여 $q$ 와 $θ$ 의 관점에서 구할 수 있습니다. 여러 참조와 함께, 적분을 평가하기 위해 요구된 단계는 Lew et al.에 의한 논문에서 구해질 것입니다;^[10] 그 결과는 다음이라는 것입니다: $b(q)={\frac {4}{9\pi }}{\biggl \{}4(q^{2}-1)K(q^{2})+(q^{2}+7)E(q^{2}){\biggr \}}$

여기서 $K$ 와 $E$ 는 첫 번째와 두 번째 종류의 완전한 타원 적분입니다.^[11] $b (0) = 2 / 3$ ; $b (1) = 32 / 9π \approx 1.13177$ .

Average distance to an arbitrary external point

The average distance from a disk to an external point

외부 위치로 전환하여, 우리는 유사한 방법에서 적분을 설정할 수 있습니다. 이번에는 다음을 얻습니다: $b(q)={\frac {2}{3\pi }}\int _{0}^{{\textrm {sin}}^{-1}{\tfrac {1}{q}}}{\biggl \{}s_{+}(\theta )^{3}-s_{-}(\theta )^{3}{\biggr \}}{\textrm {d}}\theta$

여기서 코사인의 법칙은 $s + (θ)$ 와 $s - (θ)$ 가 다음 방정식의 $s$ 에 대해 근임을 말해줍니다: $s^{2}-2qs\,{\textrm {cos}}\theta +q^{2}\!-\!1=0.$

따라서 $b(q)={\frac {4}{3\pi }}\int _{0}^{{\textrm {sin}}^{-1}{\tfrac {1}{q}}}{\biggl \{}3q^{2}{\textrm {cos}}^{2}\theta {\sqrt {1-q^{2}{\textrm {sin}}^{2}\theta }}+{\Bigl (}1-q^{2}{\textrm {sin}}^{2}\theta {\Bigr )}^{\tfrac {3}{2}}{\biggl \}}{\textrm {d}}\theta .$

우리는 다음을 얻기 위해 $u = q sinθ$ 치환할 수 있습니다: ${\begin{aligned}b(q)&={\frac {4}{3\pi }}\int _{0}^{1}{\biggl \{}3{\sqrt {q^{2}-u^{2}}}{\sqrt {1-u^{2}}}+{\frac {(1-u^{2})^{\tfrac {3}{2}}}{\sqrt {q^{2}-u^{2}}}}{\biggr \}}{\textrm {d}}u\\[0.6ex]&={\frac {4}{3\pi }}\int _{0}^{1}{\biggl \{}4{\sqrt {q^{2}-u^{2}}}{\sqrt {1-u^{2}}}-{\frac {q^{2}-1}{q}}{\frac {\sqrt {1-u^{2}}}{\sqrt {q^{2}-u^{2}}}}{\biggr \}}{\textrm {d}}u\\[0.6ex]&={\frac {4}{3\pi }}{\biggl \{}{\frac {4q}{3}}{\biggl (}(q^{2}+1)E({\tfrac {1}{q^{2}}})-(q^{2}-1)K({\tfrac {1}{q^{2}}}){\biggr )}-(q^{2}-1){\biggl (}qE({\tfrac {1}{q^{2}}})-{\frac {q^{2}-1}{q}}K({\tfrac {1}{q^{2}}}){\biggr )}{\biggr \}}\\[0.6ex]&={\frac {4}{9\pi }}{\biggl \{}q(q^{2}+7)E({\tfrac {1}{q^{2}}})-{\frac {q^{2}-1}{q}}(q^{2}+3)K({\tfrac {1}{q^{2}}}){\biggr \}}\end{aligned}}$ 이때 표준 적분을 사용합니다.^[12]

따라서 다시 $b (1) = 32 / 9π$ 이고, 반면에 역시 다음입니다^[13] $\lim _{q\to \infty }b(q)=q+{\tfrac {1}{8q}}.$

Computation

완전한 타원 적분은 산술-기하 평균(arithmetic-geometric mean) 방법에 의해 계산될 수 있습니다.^[14] $b (q)$ 는 그런-다음 다음 줄을 따라 코드에 의해 좋은 정확도로 결정될 수 있습니다:

  double discdist(double q)
  { double x,a,b,c,oldc,adash,mult,csum,K,KminusE,qsq,pi=3.141592653589793 ; 
    if(q==0) return 2.0/3.0 ; else q = fabs(q) ;
    if(q==1) return 32/(9*pi) ;
    qsq = q * q ; 
    if(q<1) x = qsq ; else x = 1/qsq ; 
  
    // agm
    b = sqrt(1-x) ;
    c = sqrt(x) ; 
    for(a=1,oldc=c+1,csum=c*c/2,mult=1;c>1e-15&&c<oldc;csum+=mult*c*c,mult*=2)
    { oldc = c ; c = (a-b)/2 ; adash = (a+b)/2 ; b = sqrt(a*b) ; a = adash ; }
    K = pi / (2*a) ;
    KminusE = K * csum ; 
  
    if(q<1) return (4/(9*pi)) * ((5*qsq+3)*K   - (qsq+7)*KminusE) ;
    else    return (4/(9*pi)) * ((5*qsq+3)*K/q - (qsq+7)*KminusE*q) ;
  }

References

^ ^a ^b Clapham, Christopher; Nicholson, James (2014), The Concise Oxford Dictionary of Mathematics, Oxford University Press, p. 138, ISBN 9780199679591.
^ Arnold, B. H. (2013), Intuitive Concepts in Elementary Topology, Dover Books on Mathematics, Courier Dover Publications, p. 58, ISBN 9780486275765.
^ Rotman, Joseph J. (2013), Journey into Mathematics: An Introduction to Proofs, Dover Books on Mathematics, Courier Dover Publications, p. 44, ISBN 9780486151687.
^ Altmann, Simon L. (1992). Icons and Symmetries. Oxford University Press. ISBN 9780198555995. disc circular symmetry.
^ Maudlin, Tim (2014), New Foundations for Physical Geometry: The Theory of Linear Structures, Oxford University Press, p. 339, ISBN 9780191004551.
^ Cohen, Daniel E. (1989), Combinatorial Group Theory: A Topological Approach, London Mathematical Society Student Texts, vol. 14, Cambridge University Press, p. 79, ISBN 9780521349369.
^ In higher dimensions, the Euler characteristic of a closed ball remains equal to +1, but the Euler characteristic of an open ball is +1 for even-dimensional balls and −1 for odd-dimensional balls. See Klain, Daniel A.; Rota, Gian-Carlo (1997), Introduction to Geometric Probability, Lezioni Lincee, Cambridge University Press, pp. 46–50.
^ Arnold (2013), p. 132.
^ Arnold (2013), Ex. 1, p. 135.
^ ^a ^b J. S. Lew et al., "On the Average Distances in a Circular Disc" (1977).
^ Abramowitz and Stegun, 17.3.
^ Gradshteyn and Ryzhik 3.155.7 and 3.169.9, taking due account of the difference in notation from Abramowitz and Stegun. (Compare A&S 17.3.11 with G&R 8.113.) This article follows A&S's notation.
^ Abramowitz and Stegun, 17.3.11 et seq.
^ Abramowitz and Stegun, 17.6.

[odm-1] Clapham, Christopher; Nicholson, James (2014), The Concise Oxford Dictionary of Mathematics, Oxford University Press, p. 138, ISBN 9780199679591.

[2] Arnold, B. H. (2013), Intuitive Concepts in Elementary Topology, Dover Books on Mathematics, Courier Dover Publications, p. 58, ISBN 9780486275765.

[3] Rotman, Joseph J. (2013), Journey into Mathematics: An Introduction to Proofs, Dover Books on Mathematics, Courier Dover Publications, p. 44, ISBN 9780486151687.

[4] Altmann, Simon L. (1992). Icons and Symmetries. Oxford University Press. ISBN 9780198555995. disc circular symmetry.

[5] Maudlin, Tim (2014), New Foundations for Physical Geometry: The Theory of Linear Structures, Oxford University Press, p. 339, ISBN 9780191004551.

[6] Cohen, Daniel E. (1989), Combinatorial Group Theory: A Topological Approach, London Mathematical Society Student Texts, vol. 14, Cambridge University Press, p. 79, ISBN 9780521349369.

[7] In higher dimensions, the Euler characteristic of a closed ball remains equal to +1, but the Euler characteristic of an open ball is +1 for even-dimensional balls and −1 for odd-dimensional balls. See Klain, Daniel A.; Rota, Gian-Carlo (1997), Introduction to Geometric Probability, Lezioni Lincee, Cambridge University Press, pp. 46–50.

[8] Arnold (2013), p. 132.

[9] Arnold (2013), Ex. 1, p. 135.

[lew-10] J. S. Lew et al., "On the Average Distances in a Circular Disc" (1977).

[11] Abramowitz and Stegun, 17.3.

[12] Gradshteyn and Ryzhik 3.155.7 and 3.169.9, taking due account of the difference in notation from Abramowitz and Stegun. (Compare A&S 17.3.11 with G&R 8.113.) This article follows A&S's notation.

[13] Abramowitz and Stegun, 17.3.11 et seq.

[14] Abramowitz and Stegun, 17.6.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]