Intermediate value theorem

Original article: w:Intermediate value theorem

Not to be confused with the Mean value theorem.

Intermediate value theorem: Let f be a defined continuous function on [a, b] and let s be a number with f(a) < s < f(b). Then there exists at least one x with f(x) = s

수학적 해석학(mathematical analysis)에서, 사잇값 정리(intermediate value theorem)는 만약 f가 그것의 도메인(domain)으로 구간(interval), [a, b]를 포함하는 연속 함수(continuous function)이면, 그것이 구간 내의 어떤 점에서 f(a)와 f(b) 사이의 임의의 주어진 값을 취한다는 것입니다.

이것은 둘의 중요한 따름정리(corollary)를 가집니다:

1. 만약 연속 함수가 구간 안에서 반대 부호의 값을 가지면, 그것은 해당 구간에서 적어도 하나의 근을 가집니다 (볼차노의 정리(Bolzano's theorem)).
2. 구간에 걸쳐 연속 함수의 이미지(image)는 그 자제로 구간입니다.

Motivation

The intermediate value theorem

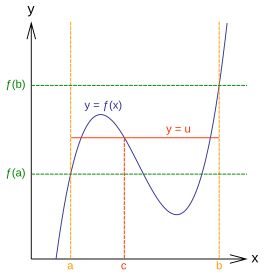
이것은 실수(real number)에 걸쳐 연속 함수의 직관적인 속성을 포착합니다: 알려진 값 f(1) = 3과 f(2) = 5를 갖는 [1, 2]에서 연속인 f가 주어지면, y = f(x)의 그래프가 x가 1에서 2로 이동하는 동안 수평 직선 y = 4를 반드시 통과해야 합니다. 그것은 닫힌 구간 위에서 연속 함수의 그래프가 종이에서 연필을 떼는 것없이 그려질 수 있다는 아이디어를 나타냅니다.

Theorem

사잇값 정리는 다음임을 말합니다:

실수 $\mathbb {R}$의 구간 $I=[a,b]$와 연수 함수 $f\colon I\to \mathbb {R}$을 생각해 보십시오. 그런-다음

• 버전 I. 만약 $u$가 $f(a)$와 $f(b)$ 사이의 숫자이면,

즉, $\min(f(a),f(b))<u<\max(f(a),f(b))$이면,

$f(c)=u$를 만족하는 $c\in (a,b)$가 있습니다.

• 버전 II. 이미지 집합(image set) $f(I)$가 역시 구간이면, 그것은 ${\bigl [}\min(f(a),f(b)),\max(f(a),f(b)){\bigr ]}$을 포함합니다.

주의: 버전 II는 함숫값의 집합(set)이 틈을 가지지 않음을 말합니다. 임의의 두 함숫값 $c<d$에 대해, 심지어 그것들이 $f(a)$와 $f(b)$ 사이의 구간 밖이면, 구간 ${\bigl [}c,d{\bigr ]}$에서 모든 점은 역시 다음 함숫값입니다:

${\bigl [}c,d{\bigr ]}\subseteq f(I)$.

구간 틈을 갖지 않는 실수의 부분집합은 구간입니다. 버전 I은 버전 II에 자연스럽게 포함됩니다.

Relation to completeness

그 정리는 실수의 완전성(completeness of the real numbers)에 의존하고, 그것과 동등합니다. 사잇값 정리는 유리수(rational number) ℚ에 적용되지 않는데 왜냐하면 틈이 유리수 사이에 존재하기 때문입니다; 무리수(irrational numbers)는 그것들의 틈을 채웁니다. 예를 들어, $x\in \mathbb {Q}$에 대해 함수 $f(x)=x^{2}-2$는 $f(0)=-2$과 $f(2)=2$를 만족시킵니다. 어쨌든, $f(x)=0$를 만족하는 유리수 $x$가 없는데, 왜냐하면 ${\sqrt {2}}$는 무리수이기 때문입니다.

Proof

그 정리는 다음과 같이 실수의 완전성(completeness) 속성의 결과로 입증될 수 있습니다:

우리는 첫 번째 경우, $f(a)<u<f(b)$를 입증해야 합니다. 두 번째 경우도 비슷합니다.

$S$를 $f(x)\leq u$를 만족하는 모든 $x\in [a,b]$의 집합으로 놓습니다. 그런-다음 $S$는 비-빈인데 왜냐하면 $a$가 $S$의 원소이고, $S$가 $b$에 의해 위로 경계져 있기 때문입니다. 따라서, 완전성에 의해, 상한(supremum) $c=\sup S$이 존재합니다. 즉, $c$는 $S$의 모든 각 원소에 대해 더 크거나 같은 가장-작은 숫자입니다. 우리는 $f(c)=u$임을 주장합니다.

어떤 $\varepsilon >0$를 고정하십시오. $f$가 연속이므로, $|x-c|<\delta$일 때마다 $|f(x)-f(c)|<\varepsilon$를 만족하는 $\delta >0$가 있습니다. 이것은 모든 $x\in (c-\delta ,c+\delta )$에 대해 다음임을 의미합니다:

$f(x)-\varepsilon <f(c)<f(x)+\varepsilon$

상한의 속성에 의해, $S$에 포함되는 어떤 $a^{*}\in (c-\delta ,c]$가 존재하고, 따라서 다음입니다:

$f(c)<f(a^{*})+\varepsilon \leq u+\varepsilon$.

$a^{**}\in (c,c+\delta )$를 선택하여, 우리는 $a^{**}\mathbb {N} ot\in S$임을 아는데 왜냐하면 $c$가 $S$의 상한이기 때문입니다. 이것은 다음임을 의미합니다:

$f(c)>f(a^{**})-\varepsilon \ >u-\varepsilon$.

부등식 둘 다는

$u-\varepsilon <f(c)<u+\varepsilon$

우리가 말했던 것처럼 오직 가능한 값으로 $f(c)=u$를 추론하는 것으로부터 모든 $\varepsilon >0$에 대해 유효합니다.

주의: 사잇값 정리는 역시 비-표준 해석학(non-standard analysis)의 방법을 사용하여 입증될 수 있으며, 이것은 엄격한 기준에 무한소를 포함하는 "직관적인" 주장을 놓습니다.

History

그 정리는 1817년에 처음으로 버나드 볼차노(Bernard Bolzano)에 의해 입증되었습니다. 볼차노는 정리의 다음 공식을 사용했습니다:

$f,\phi$를 $f(\alpha )<\phi (\alpha )$와 $f(\beta )>\phi (\beta )$를 만족하는 $\alpha$와 $\beta$ 사이의 구간 위의 연속 함수로 놓습니다. 그런-다음 $f(x)=\phi (x)$를 만족하는 $\alpha$와 $\beta$ 사이의 $x$가 있습니다.

이 공식과 현대의 공식 사이의 동등성은 $\phi$를 적절한 상수 함수로 설정함으로써 보일 수 있습니다. 오귀스탱-루이 코시(Augustin-Louis Cauchy)는 1821년에 현대의 공식과 증명을 제공했습니다. 두 사람 모두는 함수의 해석과 조제프-루이 라그랑주(Joseph-Louis Lagrange)의 연구를 공식화하려는 목표에서 영감을 받았습니다. 연속 함수가 사잇값 속성을 갖는다는 아이디어는 더 이른 기원을 가지고 있습니다. 시몬 스테빈(Simon Stevin)은 해의 십진 확장을 구성하는 것에 대해 알고리듬을 제공함으로써 (예제로 삼차(cubic)를 사용하여) 다항식(polynomial)에 대해 사잇값 정리를 입증했습니다. 그 알고리듬은 반복적으로 구간을 10 개의 부분으로 세분화하여, 반복의 각 단계에서 추가적인 십진 자릿수를 생성합니다. 연속성의 공식적인 정의가 제공되기 전에, 사잇값 속성이 연속 함수 정의의 일부로 제공되었습니다. 지지자들은 루이 알보가스트(Louis Arbogast)를 포함하며, 그는 함수에 점프가 없고, 사잇값 속성을 만족시키고 그것의 크기가 변수의 증분의 크기에 해당하는 증분을 가진다고 가정합니다. 더 이전 저자들은 그 결과를 직관적으로 분명하고 증명이 필요하지 않다고 생각했습니다. 볼차노와 코시의 통찰은 연속성의 일반적인 개념을 정의하고 (코시의 경우에서 무한소(infinitesimal)의 관점에서 및 볼차노의 경우에서 실제 부등식을 사용하여), 그러한 정의에 기초하는 증명을 제공하는 것이었습니다.

Generalizations

사잇값 정리는 연결성(connectedness)의 토폴로지적(topological) 개념과 밀접하게 연결되고 특히 ℝ의 연결된 부분집합과 메트릭 공간에서 연결된 집합의 기본 속성에서 따릅니다:

• 만약 $X$와 $Y$가 메트릭 공간(metric space), $f\colon X\to Y$가 연속 맵이고, $E\subset X$가 연결된(connected) 부분집합이면, $f(E)$는 연결된 것입니다. (*)
• 부분집합 $E\subset \mathbb {R}$이 연결된 것인 것과 그것이 다음 속성: $x,y\in E,\ x<r<y\implies r\in E$을 만족시키는 것은 필요충분 조건입니다. (**)

사실, 연결성은 토폴로지적 속성(topological property)이고 (*)은 토폴로지적 공간(topological property)으로 일반화합니다: 만약 $X$와 $Y$가 토폴로지적 공간, $f\colon X\to Y$가 연속 맵이고, $X$가 연결된 공간(connected space)이면, $f(X)$는 연결된 것입니다. 연속 맵 아래에서 연결성의 보존은 사잇값 정리, 실수 변수의 실수 값 함수 속성을 일반 공간의 연속 함수로 일반화한 것으로 생각될 수 있습니다.

이전에 말했던, 사잇값 정리의 첫 번째 버전을 상기해 보십시오:

사잇값 정리. (버전 I). 실수 $\mathbb {R}$에서 닫힌 구간 $I=[a,b]$과 연속 함수 $f\colon I\to \mathbb {R}$를 생각해 보십시오. 그런-다음, 만약 $u$가 $\min(f(a),f(b))<u<\max(f(a),f(b))$를 만족하는 실수이면, $f(c)=u$를 만족하는 $c\in (a,b)$가 존재합니다.

사잇값 정리는 이들 두 연결성 속성의 즉각적인 결과입니다:

증명: (**)에 의해, $I=[a,b]$는 연결된 집합입니다. 그것은 이미지, $f(I)$가 역시 연결된 것이라는 것에서 따릅니다. 편의상, $f(a)<f(b)$임을 가정합니다. 그런-다음 한 번 더 (**)를 호출하여, $f(a)<u<f(b)$가 어떤 $c\in I$에 대해 $u\in f(I)$, 또는 $f(c)=u$임을 의미합니다. $u\mathbb {N} eqf(a),f(b)$이므로, $c\in (a,b)$는 실제로 유지되어야 하고, 희망된 결과가 따릅니다. 같은 논증은 만약 $f(b)<f(a)$이면 적용되므로, 우리는 끝냈습니다.$\ \ \blacksquare$

사잇값 정리는 자연스러운 방법에서 일반화합니다: X가 연결된 토폴로지적 공간이고 (Y, <)가 순서 토폴로지(order topology)를 갖춘 전체적으로 순서화된(totally ordered) 집합이라고 가정하고, f : X → Y를 연속 맵이라고 놓습니다. 만약 a와 b가 X에서 두 점이고 u가 <에 관한 f(a)와 f(b) 사이에 놓인 Y에서 한 점이면, f(c) = u를 만족하는 X에서 c가 존재합니다. 원래 정리는 ℝ이 연결된 것이고 그것의 자연스러운 토폴로지(topology)가 순서 토폴로지라는 점을 주목함으로써 회복됩니다.

브라우어르 고정된-점 정리(Brouwer fixed-point theorem)는, 일 차원에서, 사잇값 정리의 특별한 경우를 제공하는 관련된 정리입니다.

Converse is false

다르부 함수(Darboux function)는 "사잇값 속성"을 갖는, 즉, 사잇값 정리의 결론을 만족시키는 실수-값 함수 f입니다: f의 도메인에 있는 두 값 a와 b, 및 f(a)와 f(b) 사이의 임의의 y에 대해, f(c) = y를 갖는 a와 b 사이에 어떤 c가 있습니다. 사잇값 정리는 모든 각 연속 함수가 다르부 함수라고 말합니다. 어쨌든, 모든 각 다르부 함수가 연속인 것은 아닙니다; 즉, 사잇값 정리의 전환은 거짓입니다.

예제로서, x > 0와 f(0) = 0에 대해 f(x) = sin(1/x)에 의해 정의된 함수 f : [0, ∞) → [−1, 1]를 취하십시오. 이 함수는 x = 0에서 연속이 아닌데 왜냐하면 f(x)의 극한(limit)은 x가 0으로 경향일 때 존재하지 않기 때문입니다; 여전히 함수는 사잇값 속성을 가집니다. 또 다른, 보다 복잡한 예제는 콘웨이 밑수 13 함수(Conway base 13 function)에 의해 제공됩니다.

실제로, 다르부의 정리(Darboux's theorem)는 어떤 구간 위에 어떤 다른 함수의 미분(differentiation)으로 인해 발생하는 모든 함수는 사잇값 속성(intermediate value property)을 가진다고 말합니다 (심지어 그것들이 연속일 필요도 없습니다).

역사적으로, 이 사잇값 속성은 실수-값 함수의 연속성에 대해 정의로 제안되어 왔습니다; 이 정의는 채택되지 않았습니다.

Practical applications

비슷한 결과는 보르수크–울람 정리(Borsuk–Ulam theorem)이며, 이것은 $n$-구에서 유클리드 $n$-공간으로의 연속 맵이 항상 몇 쌍의 대척 점을 같은 위치에 매핑할 것이라고 말합니다.

1-차원 경우에 대해 증명: $f$를 원 위의 임의의 연속 함수로 취하십시오. 원의 중심을 통과하는 직선을 그려서, 그것을 둘의 반대쪽 점 $A$와 $B$에서 교차합니다. $d$를 $f(A)-f(B)$로 정의합니다. 만약 직선이 180도 회전하면, 값 −d가 대신 얻어질 것입니다. 사잇값 정리로 인해, d = 0인 중간 회전 각도가 있어야 하고, 결과적으로 이 각도에서 f(A) = f(B)입니다.

일반적으로, 그것의 도메인이 닫힌 볼록한 $n$-차원 모양인 임의의 함수와 모양 내부의 임의의 점에 대해 (반드시 중심이 아님), 그것의 함수 값이 같은 주어진 점에 관해 둘의 대척 점이 존재합니다. 다음과 같은 주어진 점에 대해 두 개의 대 반점이 존재합니다.

그 정리는 역시 흔들리는 테이블을 회전하는 것이 안정성을 가져오는 이유의 설명을 뒷받침합니다 (특정 쉽게 충족되는 제약 조건을 필요로 합니다).

See also

• Mean value theorem
• Hairy ball theorem

External links

• Intermediate value theorem at ProofWiki
• Intermediate value Theorem - Bolzano Theorem at cut-the-knot
• Bolzano's Theorem by Julio Cesar de la Yncera, Wolfram Demonstrations Project.
• Weisstein, Eric W. "Intermediate Value Theorem". MathWorld.
• Belk, Jim (January 2, 2012). "Two-dimensional version of the Intermediate Value Theorem". Stack Exchange.
• Mizar system proof: http://mizar.org/version/current/html/topreal5.html#T4