Monomorphism

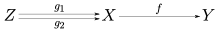
추상 대수(abstract algebra) 또는 보편 대수(universal algebra)의 맥락에서, 단사-사상(monomorphism)은 단사 준동형(homomorphism)입니다. $X$ 에서 $Y$ 로의 단사사상은 종종 $X\hookrightarrow Y$ 표기법으로 표시됩니다.

카테고리 이론(category theory)의 보다 일반적인 설정에서, 단사사상(monomorphism, 역시 monic morphism 또는 mono라고 불림)은 왼쪽-취소 사상(morphism)입니다. 즉, 모든 대상 $Z$ 와 모든 사상 $g 1, g 2 : Z \to X$ 에 대해, 다음임을 만족하는 화살 $f : X \to Y$ 입니다:

f\circ g_{1}=f\circ g_{2}\implies g_{1}=g_{2}.

단사사상은 단사 함수 (역시 "일-대-일 함수"라고 불림)의 카테고리적 일반화입니다; 일부 카테고리에서, 그 개념이 일치하지만, 단사사상이 아래 예제에서와 같이 더 일반적입니다.

포셋(posets)의 설정에서, 교집합은 거듭상등(idempotent)입니다; 어떤 것과 자신과의 교집합은 그 자체입니다. 단사사상은 이 속성을 임의적인 카테고리로 일반화합니다. 사상은 만약 그것이 당김(pullbacks)에 관해 거듭상등이면 단사사상입니다.

단사사상의 카테고리적 이중(categorical dual)은 전사사상(epimorphism)입니다. 즉, 카테고리 C에서 단사사상은 이중 카테고리(dual category) C^op에서 전사-사상입니다. 모든 각 섹션(section)은 단사사상이고, 모든 각 수축(retraction)은 전사사상입니다.

Relation to invertibility

왼쪽-역가능 사상은 반드시 단사-사상입니다: 만약 $I$ 가 $f$ 에 대한 왼쪽 역이면 ( $I$ 가 사상이고 $l\circ f=\operatorname {id} _{X}$ 라는 의미), $f$ 는 다음과 같이 단사-사상입니다:

f\circ g_{1}=f\circ g_{2}\Rightarrow l\circ f\circ g_{1}=l\circ f\circ g_{2}\Rightarrow g_{1}=g_{2}.

왼쪽-역가능 사상은 분할 단사(split mono) 또는 섹션(section)이라고 불립니다.

어쨌든, 단사-사상은 왼쪽-역가능일 필요는 없습니다. 예를 들어, 모든 그룹의 그룹(Group)과 그들 사이의 그룹 준동형(group homomorphisms)에서, 만약 H가 G의 부분그룹이면 포함 f : H → G는 항상 단사사상입니다; 그러나 $f$ 가 카테고리에서 왼쪽 역을 가지는 것과 H가 G에서 정규 여(normal complement)를 가지는 것은 필요충분 조건입니다.

사상 f : X → Y이 단사-사상인 것과 유도된 맵 f_∗ : Hom(Z, X) → Hom(Z, Y)가, 모든 사상 h : Z → X에 대해 f_∗(h) = f ∘ h에 의해 정의되며, 모든 대상 Z에 대해 단사적(injective)입니다.

Examples

놓여있는 함수(function)가 단사적인 구체적 카테고리(concrete category)의 모든 각 사상은 단사-사상입니다; 다시 말해서, 만약 사상이 실제로 집합 사이의 함수이면, 일-대-일 함수인 임의의 사상은 반드시 카테고리적 의미에서 단사-사상일 것입니다. 집합의 카테고리에서, 그 전환은 역시 성립하므로, 단사-사상은 정확히 단사적(injective) 사상입니다. 그 전환은 하나의 생성기 위에 자유 대상(free object)이 존재하기 때문에 대수의 가장 자연적으로 발생하는 카테고리에서도 성립합니다. 특히, 그것은 모든 그룹의 카테고리, 모든 링(rings)의 카테고리, 및 임의의 아벨 카테고리(abelian category)에서 참입니다.

어쨌든, 일반적으로 모든 단사사상이 다른 카테고리에서 단사적이어야 한다는 것은 참이 아닙니다; 즉, 사상이 집합 사이의 함수인 설정이 있지만, 단사적이지 않고 여전히 카테고리적 의미에서 단사사상인 함수를 가질 수 있습니다. 예를 들어, 나눔-가능 (아벨) 그룹의 카테고리 Div와 그들 사이의 그룹 준동형(group homomorphisms)에서, 단사적이 아닌 단사-사상이 있습니다: 예를 들어 몫 맵 q : Q → Q/Z를 생각해 보십시오, 여기서 Q는 덧셈 아래에서 유리수, Z는 정수 (역시 덧셈 아래에서 그룹으로 고려됨)이고, Q/Z는 해당 몫 그룹(quotient group)입니다. 예를 들어 모든 각 정수가 0으로 매핑되는 것처럼 이것은 단사적 맵이 아닙니다. 그럼에도 불구하고, 그것은 이 카테고리에서 단사사상입니다. 이것은 q ∘ h = 0 ⇒ h = 0이라는 의미에서 이어지며, 이제 입증할 것입니다. 만약 h : G → Q이고, q ∘ h = 0이면, 여기서 G는 어떤 나눔-가능 그룹이며, h(x) ∈ Z, ∀ x ∈ G입니다. 이제 일부 x ∈ G를 고정합니다. 일반성의 손실 없이, h(x) ≥ 0임을 가정할 수 있습니다 (그렇지 않으면, 대신 −x를 선택합니다). 그런-다음, n = h(x) + 1이라고 하면, G는 나눔-가능 그룹이므로, x = ny를 만족하는 y ∈ G가 존재하므로, h(x) = n h(y)입니다. 이것으로부터, 그리고 0 ≤ h(x) < h(x) + 1 = n으로부터, 다음임이 따라옵니다:

0\leq {\frac {h(x)}{h(x)+1}}=h(y)<1

h(y) ∈ Z이므로, h(y) = 0이고, 따라서 h(x) = 0 = h(−x), ∀ x ∈ G임이 따라옵니다. 이것은 원하는 대로 h = 0이라고 말합니다.

그 의미에서 q가 단사사상이라는 사실로 이동하기 위해, 일부 사상 f, g : G → Q에 대해 q ∘ f = q ∘ g라고 가정합니다, 여기서 G는 일부 나눔-가능 그룹입니다. 그런-다음 q ∘ (f − g) = 0이며, 여기서 (f − g) : x ↦ f(x) − g(x)입니다. ((f − g)(0) = 0이고, (f − g)(x + y) = (f − g)(x) + (f − g)(y)이기 때문에, (f − g) ∈ Hom(G, Q)임이 따라옵니다). 방금 입증된 의미에서, q ∘ (f − g) = 0 ⇒ f − g = 0 ⇔ ∀ x ∈ G, f(x) = g(x) ⇔ f = g입니다. 따라서, q는 주장된 대로 단사사상입니다.

Properties

토포스(topos)에서, 모든 각 단사-사상은 이퀄라이저이고, 단사적(monic)이고 전사적(epic)인 임의의 맵은 동형사상(isomorphism)입니다.
모든 각 동형사상은 단사적(monic)입니다.

Related concepts

정규 단사사상(regular monomorphism), 극단 단사사상(extremal monomorphism), 즉각적 단사사상(immediate monomorphism), 강한 단사사상(strong monomorphism), 및 분할 단사사상(split monomorphism)의 유용한 개념도 있습니다.

단사사상은 만약 그것이 어떤 한 쌍의 평행 사상의 이퀄라이저(equalizer)이면 정규(regular)라고 말합니다.
단사사상 $\mu$ 는 만약 각 표현 $\mu =\varphi \circ \varepsilon$ 에서, 여기서 $\varepsilon$ 는 전사사상이며, 사상 $\varepsilon$ 가 자동적으로 동형사상(isomorphism)이면, 극단(extremal)이라고 말합니다.^[1]
단사사상 $\mu$ 는 만약 각 표현 $\mu =\mu '\circ \varepsilon$ 에서, 여기서 $\mu '$ 은 단사사상이고 $\varepsilon$ 가 전사사상이며, 사상 $\varepsilon$ 는 자동적으로 동형사상(isomorphism)이면 즉각적(immediate)이라고 말합니다.
단사사상 $\mu :C\to D$ 는 만약 임의의 전사사상 $\varepsilon :A\to B$ 와 임의의 사상 $\alpha :A\to C$ 와 $\beta \circ \varepsilon =\mu \circ \alpha$ 를 만족하는 $\beta :B\to D$ 에 대해, $\delta \circ \varepsilon =\alpha$ 와 $\mu \circ \delta =\beta$ 를 만족하는 사상 $\delta :B\to C$ 가 존재하면 강한(strong) 것이라고 말합니다.^[1]^[2]
단사사상 $\mu$ 는 만약 $\varepsilon \circ \mu =1$ 를 만족하는 사상 $\varepsilon$ 가 존재하면 분할(split)이라고 말합니다 (이 경우에서 $\varepsilon$ 는 $\mu$ 에 대해 왼쪽-측 역이라고 불립니다).

Terminology

동반 용어 단사사상(monomorphism)과 전사사상(epimorphism)은 원래 니콜라 부르바키(Nicolas Bourbaki)에 의해 도입되었습니다; 부르바키는 단사적 함수의 속기로 단사사상(monomorphism)을 사용합니다. 초기 카테고리 이론가들은 카테고리의 맥락에 대한 단사성의 올바른 일반화가 위에 주어진 취소 속성이라고 믿었습니다. 이것은 단사사상 맵에 대해 정확히 참은 아니지만, 매우 근접하므로, 이것은 전사사상의 경우와 달리 문제가 거의 발생하지 않습니다. 손더스 맥 레인(Saunders Mac Lane)은 집합의 놓여있는 맵이 단사적인 구체적 카테고리에서 맵인 단사사상(monomorphisms)과 그 단어의 카테고리적 의미에서 단사사상인 단사적 맵(monic maps)을 구별하려고 시도했습니다. 이 구별은 일반적으로 사용되지 않았습니다.

단사사상에 대해 또 다른 이름은 확장(extension)이지만, 이것은 다른 용도로도 사용됩니다.

References

Bergman, George (2015). An Invitation to General Algebra and Universal Constructions. Springer. ISBN 978-3-319-11478-1.
Borceux, Francis (1994). Handbook of Categorical Algebra. Volume 1: Basic Category Theory. Cambridge University Press. ISBN 978-0521061193.
"Monomorphism", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Van Oosten, Jaap (1995). "Basic Category Theory" (PDF). Brics Lecture Series. BRICS, Computer Science Department, University of Aarhus. ISSN 1395-2048.
Tsalenko, M.S.; Shulgeifer, E.G. (1974). Foundations of category theory. Nauka. ISBN 5-02-014427-4.

External links

monomorphism in nLab
Strong monomorphism in nLab

[FOOTNOTEBorceux1994-1] Borceux 1994.

[FOOTNOTETsalenkoShulgeifer1974-2] Tsalenko & Shulgeifer 1974.

[1]

[2]