Integer partition

Original article: w:Integer partition

This article is about partitioning an integer. For grouping elements of a set, see Partition of a set. For the partition calculus of sets, see Infinitary combinatorics.

Young diagrams associated to the partitions of the positive integers 1 through 8. They are arranged so that images under the reflection about the main diagonal of the square are conjugate partitions.

Partitions of n with biggest addend k

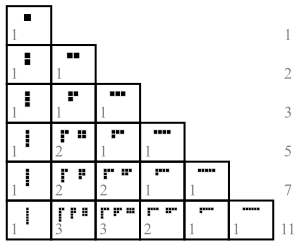
숫자 이론(number theory) 및 조합론(combinatorics)에서, 역시 정수 분할(integer partition)로 불리는, 양의 정수(integer) n의 분할(partition)은 n을 양의 정수의 합(sum)으로 쓰는 방법입니다. 오직 그들 합해지는-숫자(summand)의 순서에서 다른 두 합은 같은 분할로 여겨집니다. (만약 순서가 중요하면, 합은 합성(composition)이 됩니다.) 예를 들어 4는 다음의 다섯 구별되는 방법에서 분할될 수 있습니다:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

순서-종속적인 합성(composition) 1 + 3은 3 + 1과 같은 분할이지만, 두 구별되는 합성 1 + 2 + 1과 1 + 1 + 2은 2 + 1 + 1과 같은 분할을 나타냅니다.

분할에서 합해지는-숫자는 부분(part)으로 역시 불립니다. n의 분할의 숫자는 분할 함수 p(n)에 의해 제공됩니다. 그래서 p(4) = 5입니다. 표기법 λ ⊢ n은 λ가 n의 분할임을 의미합니다.

분할은 영 다이어그램(Young diagram) 또는 퍼얼스 다이어그램(Ferrers diagram)과 함께 그래픽적으로 시각화될 수 있습니다. 그들은 일반적으로 대칭 다항식(symmetric polynomial), 대칭 그룹(symmetric group) 및 그룹 표시 이론(group representation theory)의 연구를 포함하여 수학(mathematics) 및 물리학(physics)의 많은 가지에서 발생합니다.

Examples

5의 7 분할은 다음입니다:

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

일부 교재에서, 분할은 더하기 기호를 갖는 표현이 아니라 더해지는-숫자의 수열로 취급됩니다. 예를 들어, 분할 2 + 2 + 1은 튜플 (2, 2, 1) 또는 훨씬 더 간결한 형식 (2², 1)으로 대신 쓸 수 있으며, 여기서 위첨자는 항의 반복 횟수를 나타냅니다.

Representations of partitions

분할을 나타내는 두 가지 공통적인 다이어그램 방법이 있습니다: 그것은 노먼 매클라우드 퍼얼스(Norman Macleod Ferrers)의 이름을 따서 지은 퍼얼스 다이어그램, 및 영국의 수학자 알프레드 영(Alfred Young)의 이름을 따서 지은 영 다이어그램입니다. 둘 다는 여러 가지 가능한 관례가 있습니다; 여기서, 우리는 위-왼쪽 구석에 다이어그램을 정렬하는 영어 표기법(English notation)을 사용합니다.

Ferrers diagram

양의 숫자 14의 분할 6 + 4 + 3 + 1은 다음 다이어그램에 의해 표현될 수 있습니다:

14개 원은 각 행이 분할의 부분의 크기를 가진 4개의 행으로 정렬되어 있습니다. 숫자 4의 5 분할에 대해 다이어그램은 아래에 목록화되어 있습니다:

4	=	3 + 1	=	2 + 2	=	2 + 1 + 1	=	1 + 1 + 1 + 1

Young diagram

Main article: Young diagram

정수 분할의 대안적인 시각적 표현은 영 다이어그램(Young diagram)입니다 (역시 퍼얼스 다이어그램으로 종종 불립니다). 퍼얼스 다이어그램에서 처럼, 점과 함께 분할을 표현하는 것이 아니라, 영 다이어그램은 상자 또는 사각형을 사용합니다. 따라서, 분할 5 + 4 + 1에 대해 영 다이어그램은 다음입니다:

반면에 같은 분할에 대해 퍼얼스 다이어그램은 다음입니다:

이 겉으로 보기에 자명한 변화가 별도로 언급할만한 가치가 있어 보이지 않는 반면에, 영 다이어그램은 대칭 함수(symmetric functions) 및 그룹 표시 이론(group representation theory)의 연구에서 매우 유용함이 밝혀집니다: 다양한 규칙을 지키는 숫자 (또는 때때로 보다 복잡한 대상)을 갖는 영 다이어그램의 상자를 채우는 것은 영 타블로(Young tableaux)로 불리는 대상의 가족을 이어지고, 이들 타블로는 조합론적 및 표시-이론적 중요성을 가집니다. 함께 어울려 인접한 사각형에 의해 만들어진 유형에서 처럼, 영 다이어그램은 폴리오미노(polyomino)의 특별한 종류입니다.

Partition function

분할 함수(partition function) $p(n)$은 비-음의 정수 $n$의 가능한 분할(partitions)의 숫자(number)를 나타냅니다. 예를 들어, $p(4)=5$인데 왜냐하면 정수 $4$는 다섯 분할 $1+1+1+1$, $1+1+2$, $1+3$, $2+2$, 및 $4$를 가집니다.

$n=0,1,2,\dots$에 대해 이 함수의 값은 다음입니다:

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (OEIS에서 수열 A000041).

분할 함수에 대해 닫힌-형식 표현(closed-form expression)은 알려져 있지 않지만, 그것은 정확하게 근사하는 점근 전개(asymptotic expansions) 및 그것이 정확하게 계산될 수 있는 재귀 관계(recurrence relation) 둘 다를 가집니다. 그것은 논증의 제곱근(square root)의 지수 함수(exponential function)로 증가합니다. 그것의 생성하는 함수(generating function)의 곱셈의 역(multiplicative inverse)은 오일러 함수(Euler function)입니다; 오일러의 오각 숫자 정리(pentagonal number theorem)에 의해, 이 함수는 그 인수의 오각 숫자(pentagonal number) 거듭-제곱의 교대하는 합입니다.

스리미바자 라마누젠(Srinivasa Ramanujan)은 먼저 분할 함수가 모듈러 산술(modular arithmetic)에서 비-자명한 패턴을 가지고 있음을 발견했으며, 지금 라마누젠의 합동(Ramanujan's congruences)으로 알려져 있습니다. 예를 들어, $n$의 십진수 표시가 자릿수 4 또는 9로 끝날 때마다, $n$의 파티션의 숫자는 5로 나누어질 것입니다.

Restricted partitions

조합론과 숫자 이론 둘 다에서, 다양한 제한을 받는 분할의 가족이 종종 연구됩니다. 이 섹션은 몇 개의 그러한 제한을 조사합니다.

Conjugate and self-conjugate partitions

만약 우리가 그의 주요 대각선을 따라 분할 6 + 4 + 3 + 1의 그림을 뒤집으면, 우리는 14의 또 다른 분할을 얻습니다:

	↔
6 + 4 + 3 + 1	=	4 + 3 + 3 + 2 + 1 + 1

행을 열로 바꿈으로써, 우리는 숫자 14의 분할 4 + 3 + 3 + 2 + 1 + 1을 얻습니다. 그러한 분할은 서로의 켤레로 말합니다. 숫자 4의 경우에서, 분할 4 및 1 + 1 + 1 + 1은 켤레 쌍이고, 분할 3 + 1 및 2 + 1 + 1은 서로의 켤레입니다. 물론 흥미는 분할 2 + 2이며, 이것은 켤레로 자신을 가집니다. 그러한 분할은 자기-켤레로 말합니다.

주장: 자체-켤레 분할의 숫자는 구별하는 홀수 부분을 갖는 분할의 숫자와 같습니다.

증명 (개요): 치명적인 관찰은 모든 각 홀수 부분이 자기-켤레 다이어그램을 형성하기 위해 중간에서 "접힐" 수 있다는 것입니다.

↔

우리는 그런-다음, 다음 예제에서 묘사된 것처럼, 구별되는 홀수 부분을 갖는 분할의 집합과 자체-켤레 분할의 집합 사이의 전단사를 얻을 수 있습니다:

	↔
9 + 7 + 3	=	5 + 5 + 4 + 3 + 2
Dist. odd		self-conjugate

Odd parts and distinct parts

숫자 8의 22 분할 사이에, 오직 홀수 부분을 포함하는 6가 있습니다:

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

대안적으로, 우리는 숫자가 한 번보다 많이 발생하는 않는 분할을 셀 수 있습니다. 그러한 분할은 구별되는 부분을 갖는 분할로 불립니다. 만약 우리가 구별되는 부분을 갖는 8의 분할을 세면, 우리는 역시 6을 얻습니다:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

이것은 일반적인 속성입니다. 각 양수에 대해, 홀수 부분을 갖는 분할의 숫자는 q(n)으로 표시되는 구별되는 부분을 갖는 분할의 숫자와 같습니다. 이 결과는 1748년에 레온하르트 오일러(Leonhard Euler)에 의해 입증되었고 나중에 글레이셔의 정리(Glaisher's theorem)로 일반화되었습니다.

모든 제한된 분할의 모든 각 유형에 대해, 주어진 제한을 만족시키는 분할의 숫자에 대해 해당하는 함수가 있습니다. 중요한 예제는 q(n)입니다. q(n)의 처음 몇 개의 값은 (q(0)=1로 시작하여) 다음입니다:

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (OEIS에서 수열 A000009).

q(n)에 대해 생성하는 함수(generating function) (구별되는 부분으로 분할)는 다음에 의해 제공됩니다:

$\sum _{n=0}^{\infty }q(n)x^{n}=\prod _{k=1}^{\infty }(1+x^{k})=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.$

오각 숫자 정리(pentagonal number theorem)는 q에 대해 재귀를 제공합니다:

q(k) = a_k + q(k − 1) + q(k − 2) − q(k − 5) − q(k − 7) + q(k − 12) + q(k − 15) − q(k − 22) − ...

여기서 a_k는 만약 일부 정수 m에 대해 k = 3m² − m이면 (−1)^m이고 그렇지 않으면 0입니다.

Restricted part size or number of parts

켤레를 취함으로써, n의 정확히 k 부분으로 나누는 분할의 숫자 p_k(n)는 가장 큰 부분이 크기 k인 n의 분할의 숫자와 같습니다. 함수 p_k(n)는 다음 재귀를 만족시킵니다:

p_k(n) = p_k(n − k) + p_k−1(n − 1)

이때 초기 값은 p₀(0) = 1이고 만약 $n\leq 0$ 또는 $k\leq 0$이고 n 및 k이 둘 다 영이 아니면 p_k(n) = 0입니다.

우리는 다음에 의해 함수 p(n)을 다시-덮습니다:

$p(n)=\sum _{k=1}^{n}p_{k}(n).$

고정된 k와 n 변수를 취하는, 그러한 분할에 대해 하나의 가능한 생성하는 함수는 다음입니다:

$\sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\cdot \prod _{i=1}^{k}{\frac {1}{1-x^{i}}}.$

보다 일반적으로, 만약 T가 양의 정수의 집합이면 n의 분할의 숫자는, 그의 부분의 모두가 T에 속하는, 다음 생성하는 함수(generating function)를 가집니다:

$\prod _{t\in T}(1-x^{t})^{-1}.$

이것은 변화-만들기 문제(change-making problem)를 해결하기 위해 사용될 수 있습니다 (여기서 집합 T는 이용-가능한 동전을 지정합니다). 두 가지 특별한 경우로서, 우리는 모든 부분이 1 또는 2인 n의 분할의 숫자 (또는, 동등하게, n을 1 또는 2 부분로의 분할의 숫자)는 다음임을 가집니다:

$\left\lfloor {\frac {n}{2}}+1\right\rfloor ,$

그리고 모든 부분이 1, 2 또는 3인 n의 분할의 숫자 (또는, 동등하게, n을 최대 세 부분으로의 분할의 숫자)는 (n + 3)² / 12에 가장-가까운 정수입니다.

Asymptotics

p(n)에 대해 점근 증가 비율(asymptotic growth rate)은 다음에 의해 제공됩니다:

$\log p(n)\sim C{\sqrt {n}}{\text{ as }}n\rightarrow \infty$

여기서 $C=\pi {\sqrt {\frac {2}{3}}}$입니다.

만약 A가 자연수의 집합이면, 우리는 p_A(n)를 n을 A의 원소로 나누는 분할의 숫자를 나타내는 것으로 놓습니다. 만약 A가 양의 자연 밀도(natural density) α를 소유하면 다음이고

$\log p_{A}(n)\sim C{\sqrt {\alpha n}}$

거꾸로 만약 이것 점근 속성이 p_A(n)에 대해 유지되면 A는 자연 밀도 α를 가집니다. 이 결과는 1942년에 에르되시(Erdős)에 의해 증명의 스케치와 함께 언급되었습니다.

만약 A가 유한 집합이면, 이 해석은 적용되지 않습니다 (유한 집합의 밀도는 영입니다). 만약 A가 그의 최대 공통 약수가 1인 k 원소를 가지면, 다음입니다:

$p_{A}(n)=\left(\prod _{a\in A}a^{-1}\right)\cdot {\frac {n^{k-1}}{(k-1)!}}+O(n^{k-2}).$

Partitions in a rectangle and Gaussian binomial coefficients

Main article: Gaussian binomial coefficient

우리는 부분의 숫자와 크기를 동시에 역시 극한할 수 있습니다. p(N, M; n)은 각각 최대 M 부분, 최대 N 크기의 각각을 갖는 n의 분할의 숫자를 나타내는 것으로 놓습니다. 동등하게, 이들은 그의 영 다이어그램이 M × N 사각형 안에 맞는 분할입니다. $p(N,M;n)-p(N,M-1;n)$이 n을 크기 최대 N의 정확하게 M 부분으로의 분할을 세고, 그러한 분할의 각 부분으로부터 1을 빼면 n − M을 최대 M 부분으로의 분할을 산출하는 것을 관찰함으로써 얻어지는 다음 재귀 관계가 있습니다:

$p(N,M;n)=p(N,M-1;n)+p(N-1,M;n-M)$.

가우스 이항 계수(Gaussian binomial coefficient)는 다음으로 정의됩니다:

${k+\ell \choose \ell }_{q}={k+\ell \choose k}_{q}={\frac {\prod _{j=1}^{k+\ell }(1-q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j})}}.$

가우스 이항 계수는 다음 상등에 의해 p(N, M; n)의 생성하는 함수(generating function)와 관련됩니다:

$\sum _{n=0}^{MN}p(N,M;n)q^{n}={M+N \choose M}_{q}.$

Rank and Durfee square

Main article: Durfee square

분할의 랭크는 분할이 크기 적어도 k의 적어도 k 부분을 포함하도록 가장-큰 숫자 k입니다. 예를 들어, 분할 4 + 3 + 3 + 2 + 1 + 1은 랭크 3을 가지는데 왜냐하면 그것은 ≥ 3인 3 부분을 포함하지만,  ≥ 4인 4 부분을 포함하지 않기 때문입니다. 랭크 r의 분할의 페러스 다이어그램 또는 영 다이어그램에서, 위-왼쪽에서 엔트리의 r x r 정사각형은 더피 정사각형(Durfee square)으로 알려져 있습니다:

더피 정사각형은 분할 항등식의 증명에서 조합론 안에서 응용을 가집니다. 그것은 역시 h-인덱스(h-index)의 형식에서 실질적인 의미를 가집니다.

다른 통계량은 분할의 랭크(rank of a partition) (또는 다이슨 랭크), 즉, 가장 큰 부분 $\lambda _{k}$을 갖는 k 부분의 분할에 대해 차이 $\lambda _{k}-k$로 때때로 불립니다. 이 통계량 (이것은 위에서 설명된 하나의 관련이 없음)는 라마누젠 합동(Ramanujan congruences)의 연구에서 나타납니다.

Young's lattice

Main article: Young's lattice

영 다이어그램의 포함에 의해 주어진 분할에 대한 자연스러운 부분 순서(partial order)가 있습니다. 이 부분적으로 순서화 집합은 영의 격자(Young's lattice)로 알려져 있습니다. 격자는 표시 이론(representation theory)의 문맥에서 원래 정의되었으며, 여기서 그것은, 특성 영에서, 그들의 분기하는 속성과 함께 모든 n에 대해 대칭 그룹(symmetric group) S_n의 기약 표시(irreducible representation)를 묘사하기 위해 사용됩니다. 그것은 역시 순전히 조합론적 속성에 대해 중요한 연구를 받아 왔습니다; 특히, 그것은 차이 포셋(differential poset)의 동기-부여 예제입니다.

See also

• Rank of a partition, a different notion of rank
• Crank of a partition
• Dominance order
• Factorization
• Integer factorization
• Partition of a set
• Stars and bars (combinatorics)
• Plane partition
• Polite number, defined by partitions into consecutive integers
• Multiplicative partition
• Twelvefold way
• Ewens's sampling formula
• Faà di Bruno's formula
• Multipartition
• Newton's identities
• Smallest-parts function
• A Goldbach partition is the partition of an even number into primes (see Goldbach's conjecture)
• Kostant's partition function

References

• Abramowitz, Milton; Stegun, Irene (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. United States Department of Commerce, National Bureau of Standards. ISBN 0-486-61272-4. {{cite book}}: Invalid |ref=harv (help)
• Andrews, George E. (1976). The Theory of Partitions. Cambridge University Press. ISBN 0-521-63766-X. {{cite book}}: Invalid |ref=harv (help)
• Andrews, George E.; Eriksson, Kimmo (2004). Integer Partitions. Cambridge University Press. ISBN 0-521-60090-1.
• Apostol, Tom M. (1990) [1976]. Modular functions and Dirichlet series in number theory. Graduate Texts in Mathematics. Vol. 41 (2nd ed.). New York etc.: Springer-Verlag. ISBN 0-387-97127-0. Zbl 0697.10023. (See chapter 5 for a modern pedagogical intro to Rademacher's formula).
• Bóna, Miklós (2002). A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory. World Scientific Publishing. ISBN 981-02-4900-4. (an elementary introduction to the topic of integer partitions, including a discussion of Ferrers graphs)
• Hardy, G. H.; Wright, E. M. (2008) [1938]. An Introduction to the Theory of Numbers. Revised by D. R. Heath-Brown and J. H. Silverman. Foreword by Andrew Wiles. (6th ed.). Oxford: Oxford University Press. ISBN 978-0-19-921986-5. MR 2445243. Zbl 1159.11001.
• Lehmer, D. H. (1939). "On the remainder and convergence of the series for the partition function". Trans. Amer. Math. Soc. 46: 362–373. doi:10.1090/S0002-9947-1939-0000410-9. MR 0000410. Zbl 0022.20401. Provides the main formula (no derivatives), remainder, and older form for A_k(n).)
• Gupta, Hansraj; Gwyther, C.E.; Miller, J.C.P. (1962). Royal Society of Math. Tables. Vol. Volume 4, Tables of partitions. {{cite book}}: |volume= has extra text (help) (Has text, nearly complete bibliography, but they (and Abramowitz) missed the Selberg formula for A_k(n), which is in Whiteman.)
• Macdonald, Ian G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford University Press. ISBN 0-19-853530-9. Zbl 0487.20007. (See section I.1)
• Nathanson, M.B. (2000). Elementary Methods in Number Theory. Graduate Texts in Mathematics. Vol. 195. Springer-Verlag. ISBN 0-387-98912-9. Zbl 0953.11002. {{cite book}}: Invalid |ref=harv (help)
• Rademacher, Hans (1974). Collected Papers of Hans Rademacher. Vol. v II. MIT Press. pp. 100–07, 108–22, 460–75.
• Sautoy, Marcus Du. (2003). The Music of the Primes. New York: Perennial-HarperCollins.
• Stanley, Richard P. (1999). Enumerative Combinatorics. Vol. Volumes 1 and 2. Cambridge University Press. ISBN 0-521-56069-1. {{cite book}}: |volume= has extra text (help); Invalid |ref=harv (help)
• Whiteman, A. L. (1956). A sum connected with the series for the partition function. Vol. 6. pp. 159–176. Zbl 0071.04004. {{cite book}}: |journal= ignored (help) (Provides the Selberg formula. The older form is the finite Fourier expansion of Selberg.)

External links

• "Partition", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Partition and composition calculator
• Weisstein, Eric W. "Partition". MathWorld.
• Lectures on Integer Partitions by Herbert S. Wilf
• Counting with partitions with reference tables to the On-Line Encyclopedia of Integer Sequences
• Integer partitions entry in the FindStat database
• Integer::Partition Perl module from CPAN
• Fast Algorithms For Generating Integer Partitions
• Generating All Partitions: A Comparison Of Two Encodings
• Grime, James (April 28, 2016). "Partitions - Numberphile" (video). Brady Haran. Retrieved 5 May 2016.