Proofs of trigonometric identities

Original article: w:Proofs of trigonometric identities

삼각 함수 사이의 주요 삼각 항등식(trigonometric identities)은 주로 직각 삼각형(right triangle)의 기하학을 사용하여 입증됩니다. 더 큰 각도와 음의 각도에 대해, 삼각 함수(Trigonometric functions)를 참조하십시오.

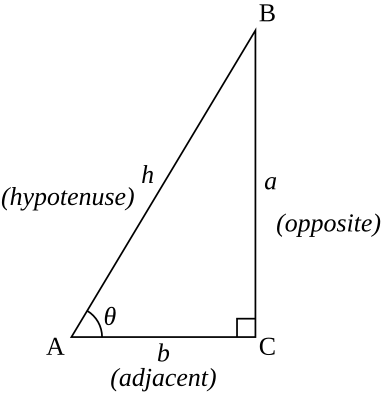
Elementary trigonometric identities

Definitions

Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle. For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse.

여섯 삼각 함수는 실수의 일부에 대해, 0으로부터 직각 (90°)의 배수만큼 다른 각도를 제외하고, 모든 각 실수(real number)에 대해 정의됩니다. 오른쪽에서 다이어그램을 참조하면, θ의 여섯 삼각 함수는 직각보다 더 작은 각도에 대한 것입니다:

$\sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}={\frac {a}{h}}$

$\cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}={\frac {b}{h}}$

$\tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {a}{b}}$

$\cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {b}{a}}$

$\sec \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}={\frac {h}{b}}$

$\csc \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}={\frac {h}{a}}$

Ratio identities

직각보다 더 작은 각도의 경우에서, 다음의 항등식은 나눗셈 항등식을 통한 위의 정의의 직접적인 결과입니다:

${\frac {a}{b}}={\frac {\left({\frac {a}{h}}\right)}{\left({\frac {b}{h}}\right)}}.$

그들은 90 °보다 큰 각도와 음의 각도에 대해 유효합니다.

$\tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}\right)}{\left({\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}\right)}}={\frac {\sin \theta }{\cos \theta }}$

$\cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {\left({\frac {\mathrm {adjacent} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {opposite} }{\mathrm {adjacent} }}\right)}}={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}$

$\sec \theta ={\frac {1}{\cos \theta }}={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}$

$\csc \theta ={\frac {1}{\sin \theta }}={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}$

$\tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {adjacent} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}}={\frac {\left({\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}\right)}}={\frac {\sec \theta }{\csc \theta }}$

또는

$\tan \theta ={\frac {\sin \theta }{\cos \theta }}={\frac {\left({\frac {1}{\csc \theta }}\right)}{\left({\frac {1}{\sec \theta }}\right)}}={\frac {\left({\frac {\csc \theta \sec \theta }{\csc \theta }}\right)}{\left({\frac {\csc \theta \sec \theta }{\sec \theta }}\right)}}={\frac {\sec \theta }{\csc \theta }}$

$\cot \theta ={\frac {\csc \theta }{\sec \theta }}$

Complementary angle identities

그들의 합이 π/2 라디안 (90도)인 두 각도는 보완적(complementary)입니다. 다이어그램에서, 꼭짓점 A와 B에서 각도는 보완적이므로, 우리는 a와 b를 교환하고, θ를 π/2 − θ로 변경하여, 다음을 얻을 수 있습니다:

$\sin \left(\pi /2-\theta \right)=\cos \theta$

$\cos \left(\pi /2-\theta \right)=\sin \theta$

$\tan \left(\pi /2-\theta \right)=\cot \theta$

$\cot \left(\pi /2-\theta \right)=\tan \theta$

$\sec \left(\pi /2-\theta \right)=\csc \theta$

$\csc \left(\pi /2-\theta \right)=\sec \theta$

Pythagorean identities

항등식 1:

$\sin ^{2}(x)+\cos ^{2}(x)=1$

다음 두 결과는 이것과 비율 항등식으로부터 따릅니다. 첫 번째를 얻기 위해, $\sin ^{2}(x)+\cos ^{2}(x)=1$의 양쪽 변을 $\cos ^{2}(x)$로 나누십시오; 두 번째에 대해, $\sin ^{2}(x)$로 나누십시오.

$\tan ^{2}(x)+1\ =\sec ^{2}(x)$

$1\ +\cot ^{2}(x)=\csc ^{2}(x)$

비슷하게

$1\ +\cot ^{2}(x)=\csc ^{2}(x)$

$\csc ^{2}(x)-\cot ^{2}(x)=1$

항등식 2:

다음은 모든 세 역수 함수를 설명합니다.

$\csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)$

증명 2:

위의 삼각형 다이어그램을 참조하십시오. 피타고라스 정리(Pythagorean theorem)에 의해 $a^{2}+b^{2}=h^{2}$임을 주목하십시오.

$\csc ^{2}(x)+\sec ^{2}(x)={\frac {h^{2}}{a^{2}}}+{\frac {h^{2}}{b^{2}}}={\frac {a^{2}+b^{2}}{a^{2}}}+{\frac {a^{2}+b^{2}}{b^{2}}}=2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}$

적절한 함수로 대체하면 -

$2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}=2\ +\tan ^{2}(x)+\cot ^{2}(x)$

다시-배열하면 다음을 제공합니다:

$\csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)$

Angle sum identities

See also: List of trigonometric identities § Angle sum and difference identities

Sine

Illustration of the sum formula.

수평 직선 (x-축)을 그리십시오; 원점 O을 표시하십시오. O로부터 수평 직선 위로 각도 $\alpha$에서 직선을 그리고 그것 위에 각도 $\beta$에서 두 번째 직선을 그리십시오; 두 번째 직선과 x-축 사시의 각도는 $\alpha +\beta$입니다.

$\alpha +\beta$에 의해 정의된 직선 위에 원점으로부터 단위 거리에 P를 위치시킵니다.

PQ를 각도 $\alpha$에 의해 정의된 직선 OQ에 수직인 직선으로 놓고, 점 P에서 이 직선 위에 점 Q로부터 그리십시오. $\therefore$ OQP는 직각 삼각형입니다.

QA를 Q에서 x-축 위에 점 A로부터 수직이고 PB를 P로부터 x-축 위에 점 B로부터 수직으로 놓습니다. $\therefore$ OAQ and OBP는 직각 삼각형입니다.

PB 위에 QR이 x-축과 평행하도록 R을 그리십시오.

이제 각도 $RPQ=\alpha$입니다 (왜냐하면 $OQA={\frac {\pi }{2}}-\alpha$이며, $RQO=\alpha ,RQP={\frac {\pi }{2}}-\alpha$로 만들고, 마침내 $RPQ=\alpha$이기 때문입니다)

$RPQ={\tfrac {\pi }{2}}-RQP={\tfrac {\pi }{2}}-({\tfrac {\pi }{2}}-RQO)=RQO=\alpha$

$OP=1$

$PQ=\sin \beta$

$OQ=\cos \beta$

${\frac {AQ}{OQ}}=\sin \alpha$, so $AQ=\sin \alpha \cos \beta$

${\frac {PR}{PQ}}=\cos \alpha$, so $PR=\cos \alpha \sin \beta$

$\sin(\alpha +\beta )=PB=RB+PR=AQ+PR=\sin \alpha \cos \beta +\cos \alpha \sin \beta$

$\beta$에 대해 $-\beta$로 치환하고 대칭(Symmetry)을 사용함으로써, 우리는 다음을 역시 얻습니다:

$\sin(\alpha -\beta )=\sin \alpha \cos(-\beta )+\cos \alpha \sin(-\beta )$

$\sin(\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$

또-다른 엄격한 증명, 및 더 쉬운 것은 복소 해석학으로부터 알려진 오일러 공식(Euler's formula)을 사용함으로써 제공됩니다. 오일러의 공식은 다음입니다:

$e^{i\varphi }=\cos \varphi +i\sin \varphi$

각도 $\alpha$와 $\beta$에 대해 따라고, 우리는 다음을 가집니다:

$e^{i(\alpha +\beta )}=\cos(\alpha +\beta )+i\sin(\alpha +\beta )$

역시 지수 함수의 다음 속성을 사용하면:

$e^{i(\alpha +\beta )}=e^{i\alpha }e^{i\beta }=(\cos \alpha +i\sin \alpha )(\cos \beta +i\sin \beta )$

곱을 평가하면:

$e^{i(\alpha +\beta )}=(\cos \alpha \cos \beta -\sin \alpha \sin \beta )+i(\sin \alpha \cos \beta +\sin \beta \cos \alpha )$

실수 및 허수 부분이 같아야 하므로:

$\cos(\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$

$\sin(\alpha +\beta )=\sin \alpha \cos \beta +\sin \beta \cos \alpha$

Cosine

위의 그림을 사용하여,

$OP=1$

$PQ=\sin \beta$

$OQ=\cos \beta$

${\frac {OA}{OQ}}=\cos \alpha$, so $OA=\cos \alpha \cos \beta$

${\frac {RQ}{PQ}}=\sin \alpha$, so $RQ=\sin \alpha \sin \beta$

$\cos(\alpha +\beta )=OB=OA-BA=OA-RQ=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta$

$\beta$에 대해 $-\beta$를 치환하고 대칭(Symmetry)을 사용함으로써, 우리는 역시 다음을 얻습니다:

$\cos(\alpha -\beta )=\cos \alpha \cos(-\beta )-\sin \alpha \sin(-\beta ),$

$\cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$

역시, 여각 공식을 사용하여,

${\begin{aligned}\cos(\alpha +\beta )&=\sin \left(\pi /2-(\alpha +\beta )\right)\\&=\sin \left((\pi /2-\alpha )-\beta \right)\\&=\sin \left(\pi /2-\alpha \right)\cos \beta -\cos \left(\pi /2-\alpha \right)\sin \beta \\&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\end{aligned}}$

Tangent and cotangent

사인 및 코사인 공식으로부터, 우리는 다음을 얻습니다:

$\tan(\alpha +\beta )={\frac {\sin(\alpha +\beta )}{\cos(\alpha +\beta )}}={\frac {\sin \alpha \cos \beta +\cos \alpha \sin \beta }{\cos \alpha \cos \beta -\sin \alpha \sin \beta }}$

분자와 분모 둘 다를 $\cos \alpha \cos \beta$로 나누어서, 우리는 다음을 얻습니다:

$\tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}$

$\alpha$로부터 $\alpha$를 빼고, $\tan(-\beta )=-\tan \beta$를 사용하여,

$\tan(\alpha -\beta )={\frac {\tan \alpha +\tan(-\beta )}{1-\tan \alpha \tan(-\beta )}}={\frac {\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }}$

비슷하게 사인 및 코사인 공식으로부터, 우리는 다음을 얻습니다:

$\cot(\alpha +\beta )={\frac {\cos(\alpha +\beta )}{\sin(\alpha +\beta )}}={\frac {\cos \alpha \cos \beta -\sin \alpha \sin \beta }{\sin \alpha \cos \beta +\cos \alpha \sin \beta }}$

그런-다음 분자와 분모 둘 다를 $\sin \alpha \sin \beta$로 나누어, 우리는 다음을 얻습니다:

$\cot(\alpha +\beta )={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}$

또는, $\cot \theta ={\frac {1}{\tan \theta }}$를 사용하여,

$\cot(\alpha +\beta )={\frac {1-\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }}={\frac {{\frac {1}{\tan \alpha \tan \beta }}-1}{{\frac {1}{\tan \alpha }}+{\frac {1}{\tan \beta }}}}={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}$

$\cot(-\beta )=-\cot \beta$를 사용하여,

$\cot(\alpha -\beta )={\frac {\cot \alpha \cot(-\beta )-1}{\cot \alpha +\cot(-\beta )}}={\frac {\cot \alpha \cot \beta +1}{\cot \beta -\cot \alpha }}$

Double-angle identities

각도 합 항등식으로부터, 우리는 다음을 얻습니다:

$\sin(2\theta )=2\sin \theta \cos \theta$

및

$\cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta$

피타고라스 항등식은 이들의 후자에 대해 두 대안적인 형식을 제공합니다:

$\cos(2\theta )=2\cos ^{2}\theta -1$

$\cos(2\theta )=1-2\sin ^{2}\theta$

각도 합 항등식은 역시 다음을 제공합니다:

$\tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}={\frac {2}{\cot \theta -\tan \theta }}$

$\cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {\cot \theta -\tan \theta }{2}}$

그것은 오일러의 공식(Euler's formula)을 사용하여 역시 입증될 수 있습니다:

$e^{i\varphi }=\cos \varphi +i\sin \varphi$

양쪽 변을 제곱하면 다음을 산출합니다:

$e^{i2\varphi }=(\cos \varphi +i\sin \varphi )^{2}$

그러나 그것의 두배된 버전을 대체하며, 이것은 방정식의 왼쪽 변과 같은 결과를 달성하며, 다음을 산출합니다:

$e^{i2\varphi }=\cos 2\varphi +i\sin 2\varphi$

그것은 다음임을 따릅니다:

$(\cos \varphi +i\sin \varphi )^{2}=\cos 2\varphi +i\sin 2\varphi$.

제곱을 전개하고 방정식의 왼쪽 변을 단순화하면 다음을 제공합니다:

$i(2\sin \varphi \cos \varphi )+\cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi +i\sin 2\varphi$.

허수 및 실수 부분은 같아야 하기 때문에, 우리는 원래 항등식을 갖게 됩니다:

$\cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi$,

및 역시

$2\sin \varphi \cos \varphi =\sin 2\varphi$.

Half-angle identities

cos 2θ에 대해 대안적인 형식을 제공하는 두 항등식은 다음 방정식으로 이어집니다:

$\cos {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}},$

$\sin {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}.$

제곱근의 부호는 적절하게 선택해야 합니다–만약 2π가 θ에 더해지면, 제곱근 내부의 양은 변하지 않지만, 방정식의 왼쪽은 부호가 바뀐다는 점에 주목하십시오. 그러므로, 사용하기에 올바른 부호는 θ의 값에 따라 다릅니다.

탄젠트 함수에 대해, 그 방정식은 다음입니다:

$\tan {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}.$

그런-다음 제곱근 내부의 분자와 분모에 (1 + cos θ)를 곱하고 피타고라스 항등식을 사용하여 다음으로 이어집니다:

$\tan {\frac {\theta }{2}}={\frac {\sin \theta }{1+\cos \theta }}.$

역시, 만약 분자와 분모가 (1 - cos θ)에 의해 둘 다 곱해지면, 그 결과는 다음입니다:

$\tan {\frac {\theta }{2}}={\frac {1-\cos \theta }{\sin \theta }}.$

이것은 역시 다음을 제공합니다:

$\tan {\frac {\theta }{2}}=\csc \theta -\cot \theta .$

코탄젠트 함수에 대해 비슷한 조작은 다음을 제공합니다:

$\cot {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta .$

Miscellaneous -- the triple tangent identity

만약 $\psi +\theta +\phi =\pi =$ 절반 원이면 (예를 들어, $\psi$, $\theta$ 및 $\phi$가 삼각형의 각도이면),

$\tan(\psi )+\tan(\theta )+\tan(\phi )=\tan(\psi )\tan(\theta )\tan(\phi ).$

증명:

${\begin{aligned}\psi &=\pi -\theta -\phi \\\tan(\psi )&=\tan(\pi -\theta -\phi )\\&=-\tan(\theta +\phi )\\&={\frac {-\tan \theta -\tan \phi }{1-\tan \theta \tan \phi }}\\&={\frac {\tan \theta +\tan \phi }{\tan \theta \tan \phi -1}}\\(\tan \theta \tan \phi -1)\tan \psi &=\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi -\tan \psi &=\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi &=\tan \psi +\tan \theta +\tan \phi \\\end{aligned}}$

Miscellaneous -- the triple cotangent identity

만약 $\psi +\theta +\phi ={\tfrac {\pi }{2}}=$ 사분의 일 원이면,

$\cot(\psi )+\cot(\theta )+\cot(\phi )=\cot(\psi )\cot(\theta )\cot(\phi )$.

증명:

$\psi$, $\theta$, 및 $\phi$의 각각을 그들의 여각으로 대체하며, 따라서 코탄젠트는 탄젠트로 바뀌고 그 반대도 마찬가지입니다.

다음이 주어지면,

$\psi +\theta +\phi ={\tfrac {\pi }{2}}$

$\therefore ({\tfrac {\pi }{2}}-\psi )+({\tfrac {\pi }{2}}-\theta )+({\tfrac {\pi }{2}}-\phi )={\tfrac {3\pi }{2}}-(\psi +\theta +\phi )={\tfrac {3\pi }{2}}-{\tfrac {\pi }{2}}=\pi$

따라서 그 결과는 세 배 탄젠트 항등식으로부터 따릅니다.

Sum to product identities

• $\sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)$
• $\cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)$
• $\cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)$

Proof of sine identities

먼저, 합-각도 항등식으로 시작합니다:

$\sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$

$\sin(\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$

이들을 함께 더함으로써,

$\sin(\alpha +\beta )+\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta +\sin \alpha \cos \beta -\cos \alpha \sin \beta =2\sin \alpha \cos \beta$

비슷하게, 두 합-각도 항등식을 뺌으로써,

$\sin(\alpha +\beta )-\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta -\sin \alpha \cos \beta +\cos \alpha \sin \beta =2\cos \alpha \sin \beta$

$\alpha +\beta =\theta$ 및 $\alpha -\beta =\phi$를 놓으면,

$\therefore \alpha ={\frac {\theta +\phi }{2}}$ and $\beta ={\frac {\theta -\phi }{2}}$

$\theta$ 및 $\phi$를 치환하면

$\sin \theta +\sin \phi =2\sin \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)$

$\sin \theta -\sin \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)=2\sin \left({\frac {\theta -\phi }{2}}\right)\cos \left({\frac {\theta +\phi }{2}}\right)$

그러므로,

$\sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)$

Proof of cosine identities

비슷하게 코사인에 대해, 합-각도 항등식으로 시작합니다:

$\cos(\alpha +\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta$

$\cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$

다시, 더하고 뺌으로써

$\cos(\alpha +\beta )+\cos(\alpha -\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta +\cos \alpha \cos \beta +\sin \alpha \sin \beta =2\cos \alpha \cos \beta$

$\cos(\alpha +\beta )-\cos(\alpha -\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta -\cos \alpha \cos \beta -\sin \alpha \sin \beta =-2\sin \alpha \sin \beta$

이전처럼 $\theta$ 및 $\phi$을 치환하면,

$\cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)$

$\cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)$

Inequalities

See also: List of triangle inequalities

Illustration of the sine and tangent inequalities.

오른쪽에서 그림은 반지름 1을 가진 원의 부채꼴을 보입니다. 부채꼴은 전체 원의 θ/(2π)이므로, 그것의 넓이는 θ/2입니다. 우리는 여기서 θ < π/2임을 가정합니다.

$OA=OD=1$

$AB=\sin \theta$

$CD=\tan \theta$

삼각형 OAD의 넓이는 AB/2, 또는 sin(θ)/2입니다. 삼각형 OCD의 넓이는 CD/2, 또는 tan(θ)/2입니다.

삼각형 OAD는 완전하게 부채꼴 내부에 놓이므로, 이것은 차례로 삼각형 OCD 내부에 완전히 놓이며, 우리는 다음을 가집니다:

$\sin \theta <\theta <\tan \theta .$

이 기하학적 논증은 가정으로 작용하는 호 길이(arc length)와 넓이(area)의 정의에 의존하며, 따라서 입증-가능한 속성보다는 오히려 삼각 함수(trigonometric functions)의 구성에서 부과되는 조건입니다. 사인 함수에 대해, 우리는 다른 값을 처리할 수 있습니다. 만약 θ > π/2이면, θ > 1입니다. 그러나 sin θ ≤ 1 (피타고라스 항등식 때문에)이므로, sin θ < θ입니다. 그래서 우리는 다음을 가집니다:

${\frac {\sin \theta }{\theta }}<1\ \ \ \mathrm {if} \ \ \ 0<\theta .$

θ의 음의 값에 대해, 우리는, 사인 함수의 대칭에 의해, 다음을 가집니다:

${\frac {\sin \theta }{\theta }}={\frac {\sin(-\theta )}{-\theta }}<1.$

그러므로

${\frac {\sin \theta }{\theta }}<1\quad {\text{if }}\quad \theta \neq 0,$

및

${\frac {\tan \theta }{\theta }}>1\quad {\text{if }}\quad 0<\theta <{\frac {\pi }{2}}.$

Identities involving calculus

Preliminaries

$\lim _{\theta \to 0}{\sin \theta }=0$

$\lim _{\theta \to 0}{\cos \theta }=1$

Sine and angle ratio identity

$\lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}=1$

다시 말해서, 함수 사인은 0에서 미분-가능differentiable이고, 그것의 도함수(derivative)는 1입니다.

증명: 이전 부등식으로부터, 우리는, 작은 각도에 대해, 다음을 가집니다:

$\sin \theta <\theta <\tan \theta$,

그러므로,

${\frac {\sin \theta }{\theta }}<1<{\frac {\tan \theta }{\theta }}$,

오른쪽 변 부등식을 생각해 보십시오. 다음이므로,

$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$

$\therefore 1<{\frac {\sin \theta }{\theta \cos \theta }}$

$\cos \theta$에 의해 양쪽 변을 곱하면,

$\cos \theta <{\frac {\sin \theta }{\theta }}$

왼쪽-변의 부등식과 결합하면:

$\cos \theta <{\frac {\sin \theta }{\theta }}<1$

$\cos \theta$를 $\theta \to 0$일 때 극한으로 취하면

$\lim _{\theta \to 0}{\cos \theta }=1$

그러므로,

$\lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}=1$

Cosine and angle ratio identity

$\lim _{\theta \to 0}{\frac {1-\cos \theta }{\theta }}=0$

증명:

${\begin{aligned}{\frac {1-\cos \theta }{\theta }}&={\frac {1-\cos ^{2}\theta }{\theta (1+\cos \theta )}}\\&={\frac {\sin ^{2}\theta }{\theta (1+\cos \theta )}}\\&=\left({\frac {\sin \theta }{\theta }}\right)\times \sin \theta \times \left({\frac {1}{1+\cos \theta }}\right)\\\end{aligned}}$

그들 세 양의 극한이 1, 0, 및 1/2이므로, 결과 극한은 영입니다.

Cosine and square of angle ratio identity

$\lim _{\theta \to 0}{\frac {1-\cos \theta }{\theta ^{2}}}={\frac {1}{2}}$

증명:

이전 증명에서 처럼,

${\frac {1-\cos \theta }{\theta ^{2}}}={\frac {\sin \theta }{\theta }}\times {\frac {\sin \theta }{\theta }}\times {\frac {1}{1+\cos \theta }}.$

그들 세 양의 극한은 1, 1, 및 1/2이므로, 결과 극한은 1/2입니다.

Proof of compositions of trig and inverse trig functions

모든 이들 함수는 피타고라스 삼각 함등식으로부터 따릅니다. 우리는 예를 들어 다음 함수를 입증할 수 있습니다:

$\sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}$

증명:

우리는 다음으로부터 시작합니다:

$\sin ^{2}\theta +\cos ^{2}\theta =1$

그런-다음 우리는 이 방정식을 $\cos ^{2}\theta$로 나누면

$\cos ^{2}\theta ={\frac {1}{\tan ^{2}\theta +1}}$

그런-다음 치환 $\theta =\arctan(x)$을 사용하고, 피타고라스 삼각 항등식을 사용합니다:

$1-\sin ^{2}[\arctan(x)]={\frac {1}{\tan ^{2}[\arctan(x)]+1}}$

그런-다음 우리는 항등식 $\tan[\arctan(x)]\equiv x$을 사용합니다:

$\sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}$

See also

• List of trigonometric identities
• Bhaskara I's sine approximation formula
• Generating trigonometric tables
• Aryabhata's sine table
• Madhava's sine table
• Table of Newtonian series
• Madhava series
• Unit vector (explains direction cosines)
• Euler's formula