Radius

Original article: w:Radius

This article is about the line segment. For the bone, see Radius (bone). For other uses, see Radius (disambiguation).

Circle with circumference C in black, diameter D in blue, radius R in red, and center or origin O in green.

고전 기하학(geometry)에서, 원(circle) 또는 구(sphere)의 반지름은 중심(center)에서 둘레(perimeter)까지의 선분(line segment) 중 임의의 것이고, 보다 현대적인 사용법에서, 그것은 역시 길이입니다. 그 이름은 반직선이지만 역시 전차 바퀴의 스포크를 의미하는 라틴어(Latin) radius에서 유래합니다. 반지름의 복수형은 radii (라틴어 복수형에서 유래) 또는 관례적인 영어 복수형 radiuses이 될 수 있습니다. 반지름에 대한 전형적인 약어와 수학적 변수(mathematical variable) 이름은 R입니다. 확장에 의해, 지름(diameter) D는 반지름의 두 배로 정의됩니다:

$d\doteq 2r\quad \Rightarrow \quad r={\frac {d}{2}}.$

만약 물체가 중심을 가지지 않으면, 그 용어는 둘레반지름(circumradius), 둘레-접하는 원(circumscribed circle) 또는 둘레-접하는 구(circumscribed sphere)의 반지름을 참조할 수 있습니다. 두 경우에서, 반지름은 지름의 절반 이상일 수 있으며, 보통 그림의 임의의 두 점 사이의 최대 거리로 정의됩니다. 기하학적 도형의 내-반지름(inradius)은 보통 그것 안에 포함된 가장 큰 원 또는 구의 반지름입니다. 링, 튜브, 또는 기타 속이 빈 물체의 내부 반지름은 공동의 반지름입니다.

정규 다각형(regular polygon)에 대해, 반지름은 둘레-반지름과 같습니다. 정규 다각형의 내-반지름은 역시 아포팀(apothem)이라고 불립니다. 그래프 이론(graph theory)에서, 그래프의 반지름(radius of a graph)은 u에서 그래프의 다른 꼭짓점까지의 최대 거리의 모든 꼭짓점 u에 걸쳐 최솟값입니다.

둘레(perimeter) (원주(circumference)) C를 갖는 원의 반지름은 다음입니다:

$r={\frac {C}{2\pi }}$

Formula

많은 기하학적 도형에 대해, 반지름은 도형의 다른 측정과 잘-정의된 관계를 가집니다.

Circles

See also: Area of a circle

넓이(area) A를 갖는 원의 반지름은 다음입니다:

$r={\sqrt {\frac {A}{\pi }}}.$

셋의 비-공선형(collinear) 점 P₁, P₂, 및 P₃를 통과하는 원의 반지름은 다음입니다:

$r={\frac {|{\vec {OP_{1}}}-{\vec {OP_{3}}}|}{2\sin \theta }},$

여기서 θ은 각도 ∠P₁P₂P₃입니다. 이 공식은 사인의 법칙(law of sines)을 사용합니다. 만약 세 점이 좌표 (x₁,y₁), (x₂,y₂), 및 (x₃,y₃)에 의해 제공되면, 반지름은 다음으로 표현될 수 있습니다:

$r={\frac {\sqrt {[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}][(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}][(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}]}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}|}}.$

Regular polygons

See also: Circumscribed circle

n	Rn
3	0.577350...
4	0.707106...
5	0.850650...
6	1.0
7	1.152382...
8	1.306562...
9	1.461902...
10	1.618033...

A square, for example (n=4)

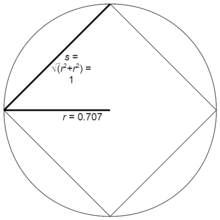
길이 s의 n 변을 갖는 정규 다각형의 반지름 r은 r = R_n s로 제공되며, 여기서 $R_{n}=1\left/\left(2\sin {\frac {\pi }{n}}\right)\right..$ n의 작은 값에 대해 R_n의 값은 테이블에서 제공됩니다. 만약 s = 1이면 이들 값은 역시 대응하는 정규 다각형의 반지름들입니다.

Hypercubes

변 s를 갖는 d-차원 초-입방체(hypercube)의 반지름은 다음과 같습니다:

$r={\frac {s}{2}}{\sqrt {d}}.$

Use in coordinate systems

Polar coordinates

Main article: Polar coordinate system

극 좌표 시스템은 평면(plane) 위에 각 점(point)이 고정된 점으로부터의 거리(distance)와 고정된 방향으로부터의 각도(angle)에 의해 결정되는 이-차원 좌표 시스템(coordinate system)입니다.

고정된 점(데카르트 시스템(Cartesian system)의 원점과 아날로그)은 극점(pole)이라고 하고, 극점으로부터 고정된 방향에서 반직선(ray)은 극 축(polar axis)이라고 합니다. 극점으로부터의 거리는 방사형 좌표(radial coordinate) 또는 반지름(radius)라고 하고, 각도는 각 좌표(angular coordinate), 극 각(polar angle) 또는 방위각(azimuth)입니다.

Cylindrical coordinates

Main article: Cylindrical coordinate system

원통 좌표 시스템에서, 선택된 참조 축과 해당 축에 수직인 선택된 참조 평면이 있습니다. 시스템의 원점은 모든 세 좌표가 영으로 주어질 수 있는 점입니다. 이것은 참조 평면과 축 사이의 교차점입니다.

축은 원점에서 시작하여 기준 방향을 가리키는 참조 평면에 놓이는 반직선(ray)인 극 축(polar axis)과 구별하기 위해 원통형(cylindrical) 또는 경도(longitudinal) 축으로 다양하게 불립니다.

축으로부터의 거리는 방사상 거리(radial distance) 또는 반지름(radius)이라고 부를 수 있고, 반면에 각의 좌표는 때때로 각의 위치(angular position) 또는 방위각(azimuth)으로 참조됩니다. 반지름과 방위각은 참조 평면에 평행한 점을 통과하는 평면에서 이-차원 극좌표 시스템에 해당하므로 함께 극 좌표(polar coordinates)라고 불립니다. 세 번째 좌표는 높이(height) 또는 고도(altitude) (참조 평면이 수평으로 고려되면), 경도 위치(longitudinal position), 또는 축 위치(axial position)라고 불릴 수 있습니다.

Spherical coordinates

Main article: Spherical coordinate system

구형 좌표 시스템에서, 반지름은 고정된 원점에서 한 점까지의 거리를 나타냅니다. 방사상 방향과 고정된 천정 방향 사이에서 측정된 극 각에 의해 추가로 정의되면 그 위치와 원점을 통과하고 천정에 직교하는 참조 평면, 및 해당 평면에서 고정된 참조 방향에서 반사상 방향의 직교 투영 사이의 각도, 방위각.

See also

• Bend radius
• Filling radius in Riemannian geometry
• Radius of convergence
• Radius of convexity
• Radius of curvature
• Radius of gyration
• Semidiameter