Regular polyhedron

정규 다면체(regular polyhedron)는 대칭 그룹(symmetry group)이 플래그(flags)에 전이적으로 동작하는 다면체(polyhedron)입니다. 정규 다면체는 고도로 대칭적이며, 가장자리-전이적, 꼭짓점-전이적, 및 면-전이적 모두 있습니다. 고전적인 맥락에서, 많은 다른 동등한 정의가 사용됩니다; 공통적인 것은 면이 각 꼭짓점 주위에서 같은 방식으로 조립되는 합동 정규 다각형입니다.

정규 다면체는 {n, m} 형식의 슐래플리 기호(Schläfli symbol)로 식별되며, 여기서 n은 각 면의 변의 개수이고 m은 각 꼭짓점에서 만나는 면의 개수입니다. 5개의 유한 볼록 정규 다면체 (플라톤 고체)와 4개의 정규 별 다면체 (케플러-푸앵소 다면체)가 있어, 모두 9개의 정규 다면체가 됩니다. 게다가, 정규 다면체에는 5개의 정규 혼합체가 있습니다.

The regular polyhedra

플라톤 고체(Platonic solids)로 알려진 5개의 볼록 정규 다각형이 있습니다; 4개의 정규 별 다면체(star polyhedra), 케플러-푸앵소 다면체(Kepler–Poinsot polyhedra); 및 정규 다면체의 5개의 정규 혼합체가 있습니다:

Platonic solids


Tetrahedron {3, 3}	Cube {4, 3}	Octahedron {3, 4}	Dodecahedron {5, 3}	Icosahedron {3, 5}
χ = 2	χ = 2	χ = 2	χ = 2	χ = 2

Kepler–Poinsot polyhedra


Small stellated dodecahedron {5/2, 5}	Great dodecahedron {5, 5/2}	Great stellated dodecahedron {5/2, 3}	Great icosahedron {3, 5/2}
χ = −6	χ = −6	χ = 2	χ = 2

Regular compounds


Two tetrahedra 2 {3, 3}	Five tetrahedra 5 {3, 3}	Ten tetrahedra 10 {3, 3}	Five cubes 5 {4, 3}	Five octahedra 5 {3, 4}
χ = 4	χ = 10	χ = 0	χ = −10	χ = 10

Characteristics

Equivalent properties

각 꼭짓점 주위에 유사한 면의 배열을 가지는 속성은 정의에서 다음과 같은 동등한 조건 중 임의의 것으로 대체될 수 있습니다:

볼록 정규 다면체의 꼭짓점 모두는 구(sphere) 위에 놓입니다.
다면체의 모든 이면 각도(dihedral angle)는 같습니다.
다면체의 모든 꼭짓점 도형(vertex figures)은 정규 다각형(regular polygons)입니다.
다면체의 모든 고체 각도(solid angles)는 합동(congruent)입니다.^[1]

Concentric spheres

볼록 정규 다면체는 그것의 중심을 공유하는 모두 세 개의 관련된 구 (다른 다면체는 적어도 한 종류가 없음)가 있습니다:

내-구(insphere), 모든 면에 접합니다.
내부-구(intersphere) 또는 중간-구(midsphere), 모든 가장자리에 접합니다.
둘레-구(circumsphere), 모든 꼭짓점에 접합니다.

Symmetry

정규 다면체는 모든 다면체 중에서 가장 대칭적(symmetrical)입니다. 그것들은 플라톤 고체의 이름을 따서 지은 단 세 개의 대칭 그룹(symmetry groups)에 있습니다:

Tetrahedral
Octahedral (or cubic)
Icosahedral (or dodecahedral)

이십면체 또는 팔면체 대칭을 갖는 임의의 모양은 사면체 대칭도 포함합니다.

Euler characteristic

5개의 플라톤 고체는 오일러 특성(Euler characteristic)이 2입니다. 이것은 단순히 표면이 토폴로지적 2-구라는 것을 반영하고, 예를 들어 일부 내부 점에 관해 별-모양인 임의의 다면체의 경우에도 참입니다.

Interior points

정규 다면체 내부에서 임의의 점에서 변까지의 거리의 합은 점의 위치와 무관합니다 (이것은 비비아니 정리의 확장입니다). 어쨌든, 그 전환은 유지되지 않고, 사면체(tetrahedra)의 경우에도 성립하지 않습니다.^[2]

Duality of the regular polyhedra

다면체의 이중(dual) 쌍에서, 한 다면체의 꼭짓점은 다른 면에 대응하고, 그 반대도 마찬가지입니다.

정규 다면체는 이 이중성을 다음과 같이 보여줍니다:

사면체(tetrahedron)는 자체-이중입니다, 즉, 그것은 자제와 쌍을 이룹니다.
육면체(cube)와 팔면체(octahedron)는 서로 이중입니다.
이십면체(icosahedron)와 십이면체(dodecahedron)는 서로 이중입니다.
작은 별-모양 십이면체(small stellated dodecahedron)와 큰 이십면체(great dodecahedron)는 서로 이중입니다.
큰 별-모양 십이면체(great stellated dodecahedron)와 큰 이십면체(great icosahedron)는 서로 이중입니다.

이중의 슐래플리 기호는 단지 원래 것을 거꾸로 쓴 것입니다. 예를 들어, {5, 3}의 이중은 {3, 5}입니다.

History

Prehistory

구형 또는 혹의 클러스터를 닮은 모양으로 조각된 돌이 스코틀랜드에서 발견되어 왔고 4,000년 정도 된 것일 수 있습니다. 이들 돌들 중 일부는 5개의 플라톤 고체의 대칭성뿐만 아니라, 그것들 사이의 이중성의 관계 (즉, 입방체 면의 중심이 팔면체의 꼭짓점을 제공함)의 일부를 보여줍니다. 이들 돌의 예제는 옥스퍼드 대학교 Ashmolean 박물관의 John Evans 방에 전시되어 있습니다. 이들 물건이 만들어진 이유나 제작자가 어떻게 영감을 얻었는지는 미스터리입니다. 많은 물체가 비-플라폰 형태를 가지고 있고, 이중 이십면체의 재해석, 십이면체와 반대로 오직 하나만이 진정한 이십면체인 것으로 밝혀졌기 때문에, 이들 물체의 수학적 해석에 대해 의문이 있습니다.^[3]

역시 에트루리아인들(Etruscans)은 19세기 후반과 2,500년 이상 거슬러 올라가는 파도바 (이탈리아 북부) 근처에서 동석(soapstone)으로 만들어진 십이면체를 발견한 것으로 입증된 바와 같이 적어도 일부 정규 다면체에 대한 인식에서 그리스인보다 앞서 있었을 가능성이 있습니다 (Lindemann, 1987).

Greeks

정규 볼록 고체에 대한 알려진 최초의 서면 기록은 고전 그리스에서 유래되었습니다. 이들 고체가 모두 발견되었을 때와 누구에 의한 것이지는 알려지지 않았지만, Theaetetus (아테네인)는 다섯 가지 모두에 대한 수학적 설명을 처음으로 제공했습니다 (Van der Waerden, 1954), (Euclid, book XIII). H.S.M. Coxeter (Coxeter, 1948, Section 1.9)는 플라톤 (기원전 400년)이 그것들의 모형을 만들었다고 공인하고, 초기 피타고라스 학파 중 한 명, Locri의 Timaeus가 당시 인식된 대로 다면체와 우주의 본질 사이의 대응에서 다섯 가지 모두를 사용했다고 언급합니다 – 이 대응은 플라톤의 대화 Timaeus에 기록되어 있습니다. 플라톤에 대한 유클리드의 참조는 플라톤 고체라는 공통적인 설명으로 이어졌습니다:

그리스 정의를 다음과 같이 특징지을 수 있습니다:

정규 다각형은 모든 가장자리가 같고 모든 모서리가 같은 (볼록) 평면 도형입니다.
정규 다면체는 모든 면이 합동인 정규 다각형이고, 각 꼭짓점 주위에 같은 숫자가 똑같이 배열된 고체 (볼록) 도형입니다.

이 정의는, 예를 들어, 정사각 각뿔 (모든 면이 정규이지만, 정사각형 밑면이 삼각형 면과 합동이기 때문), 또는 두 개의 사면체를 함께 결합함으로써 형성된 모양 (해당 삼각형 쌍각뿔의 모든 면이 등변 삼각형, 즉, 합동이고 정규이지만, 일부 꼭짓점은 3개 삼각형을 가지고 다른 것들은 4개를 가지기 때문)을 배제합니다.

정규 다면체의 이 개념은 거의 2000년 동안 도전받지 않은 채 남아 있었을 것입니다.

Regular star polyhedra

펜타그램 (별 오각형)과 같은 정규 별 다각형은 고대 그리스인에게도 알려져 있었습니다 – 펜타그램은 피타고라스 학파에서 비밀 기호로 사용했지만, 그들은 다면체를 구성하기 위해 그것들을 사용하지는 않았습니다. 요하네스 케플러(Johannes Kepler)는 17세기 초가 되어서야 펜타그램이 정규 별 다면체의 면으로 사용될 수 있다는 것을 깨달았습니다. 이들 별 다면체 중 일부는 케플러 시대 이전에 다른 사람들에 의해 발견되었을 수 있지만, 케플러는 정규 다면체가 볼록하다는 제한을 제거하면 그것들이 "정규"로 고려될 수 있음을 처음으로 인식했습니다. 200년 후 루이 푸앵소(Louis Poinsot)는 역시 별 꼭짓점 도형 (각 모서리 주위의 회로)을 허용하여, 케플러의 재발견과 함께 두 개의 새로운 정규 별 다면체를 발견할 수 있게 했습니다. 이들 4개는 유일한 정규 별 다면체이고, 케플러-푸앵소 다면체(Kepler–Poinsot polyhedra)로 알려지게 되었습니다. 19세기 중반이 되어서야, 푸앵소가 출판된 지 수십 년 후에 케일리는 그들에게 현대 영어 이름을 부여했습니다: (케플러의) 작은 별-모양 십이면체와 큰 별모양 십이면체, 및 (푸앵소의) 큰 별모양 십이면체와 큰 십이면체가 그 이름입니다.

케플러-푸앵소 다면체는 별모양화(stellation)라고 불리는 과정에 의해 플라톤 고체로부터 구성될 수 있습니다. 별모양화에 대한 역 과정은 패싯화(facetting 또는 faceting)라고 불립니다. 하나의 다면체의 모든 별모양화는 이중(dual), 또는 이중 다면체의 일부 패싯에 대해 역수입니다. 정규 별 다면체는 플라톤 고체를 패싯화함으로써 얻을 수도 있습니다. 이것은 케일리가 그것들을 이름-지었을 때 버트런드(Bertrand)에 의해 처음 수행되었습니다.

따라서 19세기 말까지 9개의 정규 다면체 – 5개의 볼록과 4개의 별이 있었습니다.

Regular polyhedra in nature

각각의 플라톤 고체는 하나 또는 다른 형태로 자연적으로 발생합니다.

사면체, 육면체, 및 팔면체는 모두 결정(crystals)으로 발생합니다. 이것들은 결정의 가능한 형태의 수를 결코 소진하지 않으며 (Smith, 1982, p212), 그 중 48개가 있습니다. 정규 이십면체도 정규 십이면체도 그들 사이에 없지만, 결정은 정규 십이면체와 시각적으로 거의 구별할 수 없는 정규 십면체의 모양을 가질 수 있습니다. 진정한 이십면체 결정은 자연계에서는 매우 드물지만 실험실에서 생산될 수 있는 준결정질 재료로 형성될 수 있습니다.

더 최근의 발견은 풀러린 (Curl, 1991 참조)으로 알려진 일련의 새로운 유형의 탄소 분자입니다. 비록 가장 쉽게 생산되는 풀러린, C₆₀이 다소 구형으로 보일지라도, (C₂₄₀, C₄₈₀, 및 C₉₆₀과 같은) 일부 더 큰 변종은 몇 나노미터인 약간 둥근 이십면체 형태를 취하는 것으로 가설됩니다.

정규 다면체는 생물학에서도 나타납니다. 원석조강(coccolithophore) Braarudosphaera bigelowii는 약 10 마이크로미터 크기의 정규 십이면체 구조를 가지고 있습니다.^[4] 20세기 초에 에른스트 헤켈(Ernst Haeckel)은 여러 종의 방산충(radiolarians)을 묘사했으며, 그 중 일부는 다양한 정규 다면체 모양의 껍데기를 가지고 있습니다.^[5] 예로는 Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus, 및 Circorrhegma dodecahedra가 있습니다; 이들 생물의 모양은 그것들의 이름으로 표시됩니다.^[5] 많은 바이러스의 외부 단백질 껍질은 정규 다면체를 형성합니다. 예를 들어, HIV는 전형적인 미오바이러스(myovirus)의 머리와 마찬가지로 정규 이십면체로 둘러싸여 있습니다.^[6]^[7]

The coccolithophore Braarudosphaera bigelowii has a regular dodecahedral structure
The radiolarian Circogonia icosahedra has a regular icosahedral structure
A myovirus typically has a regular icosahedral capsid (head) about 100 nanometers across.

고대에 피타고라스 학파는 정규 다면체와 행성의 궤도 사이에 조화가 있다고 믿었습니다. 17세기에서, 요하네스 케플러는 티코 브라헤에 의해 수집된 행성 운동에 관한 데이터를 연구했고 10년 동안 다면체의 크기와 행성 궤도의 크기 사이의 일치를 찾아 피타고라스의 이상을 확립하려고 노력했습니다. 그의 탐색은 원래 목적에 실패했지만, 이 연구를 통해 케플러는 정규 폴리토프로서의 케플러 고체에 대한 발견, 행성의 궤도가 원이 아니라는 깨달음, 및 그가 지금 유명하게 된 행성 운동의 법칙을 발견했습니다. 케플러 시대에는 단지 5개의 행성 (지구 제외)만이 알려져 있었으며, 플라톤의 고체의 숫자와 잘 일치했습니다. 케플러의 연구와 그 이후 천왕성(Uranus)과 해왕성(Neptune)의 발견은 피타고라스의 생각을 무효화했습니다.

피타고라스 학파와 거의 같은 시기에 플라톤은 다섯 가지 원소 (흙, 공기, 불, 물, 및 영혼)가 각각 다섯 가지 정규 고체 중 하나의 작은 복사본으로 구성되어 있다는 물질 이론을 설명했습니다. 물질은 이들 다면체의 혼합물로 구성되었으며, 각 물질은 혼합물에서 서로 다른 비율을 가졌습니다. 2000년 후 달튼의 원자 이론(Dalton's atomic theory)은 이 아이디어가 올바른 선을 따른다는 것을 보여주었지만, 정규 고체와 직접적으로 관련되지는 않았습니다.

Further generalisations

20세기에는 정규 다면체 아이디어가 연속적으로 일반화되어 몇 가지 새로운 클래스가 생겨났습니다.

Regular skew apeirohedra

처음 10년 동안 콕서터와 피트리는 융기 부분과 골짜기 부분이 번갈아 나타나는 "안장" 꼭짓점을 허용하여, 정규 꼬인 다면체(regular skew polyhedra)라고 불리는 3개의 무한 접힌 표면을 구성할 수 있도록 했습니다.^[8] 콕서터는 이들 도형에 대해 수정된 슐래플리 기호(Schläfli symbol) {l,m|n}을 제안했으며, {l,m}은 꼭짓점 주위에 m개의 정규 l-각형을 갖는 꼭짓점 도형(vertex figure)을 의미합니다. n은 n-각형 구멍을 정의합니다. 그것들의 꼭짓점 도형은 정규 꼬인 다각형이며, 꼭짓점은 두 평면 사이에서 지그재그로 움직입니다.

Infinite regular skew polyhedra in 3-space (partially drawn)
{4,6\|4}	{6,4\|4}	{6,6\|3}

Regular skew polyhedra

4-공간에서 유한한 정규 꼬인 다면체가 존재합니다. 4-공간에서 이들 유한 정규 꼬인 다면체는 균등 4-폴리토프(uniform 4-polytopes)의 면의 부분집합으로 볼 수 있습니다. 그것들은 평면 정규 다각형(regular polygon) 면을 가지고 있지만, 정규 꼬인 다각형(regular skew polygon) 꼭짓점 도형(vertex figures)을 가지고 있습니다.

2개의 이중 해는 5-셀과 관련이 있고, 2개의 이중 해는 24-셀과 관련이 있고, 무한 집합의 자체-이중 이중각기둥은 정규 꼬인 다면체를 {4, 4 | n}로 생성합니다. 무한 극한에서, 이것들은 이중-원기둥(duocylinder)에 접근하고 3-공간으로의 입체 투영(stereographic projections)에서 토러스(torus)처럼 보입니다.

Finite regular skew polyhedra in 4-space
Orthogonal Coxeter plane projections				Stereographic projection
A₄		F₄		Stereographic projection

{4, 6 \| 3}	{6, 4 \| 3}	{4, 8 \| 3}	{8, 4 \| 3}	{4, 4 \| n}
30 {4} faces 60 edge 20 vertices	20 {6} faces 60 edges 30 vertices	288 {4} faces 576 edges 144 vertices	144 {8} faces 576 edges 288 vertices	n² {4} faces 2n² edges n² vertices

Regular polyhedra in non-Euclidean and other spaces

비-유클리드 (쌍곡 기하학과 타원 기하학) 및 이전 세기에 걸쳐 발견된 복소 공간(complex spaces)과 같은 다른 공간에 대한 연구는 해당 공간에서 정규 기하학적 형태만 취할 수 있는 복소 다면체(complex polyhedra)와 같은 더 새로운 다면체의 발견으로 이어졌습니다.

Regular polyhedra in hyperbolic space

H³ 쌍곡선 공간(hyperbolic space)에서, 파라콤팩트 정규 벌집(paracompact regular honeycombs)은 유클리드 타일링 패싯(facets)과 유한 다면체처럼 동작하는 꼭짓점 도형(vertex figures)을 가집니다. 그러한 타일링은 한쪽 또는 다른 쪽으로 구부려 닫을 수 있는 각도 결함(angle defect)을 가집니다. 만약 타일링이 적절하게 스케일링되면, 그것은 단일 아이디얼 점(ideal point)에서 점근적 극한(asymptotic limit)으로 닫힐 것입니다. 이들 유클리드 타일링은 다면체가 구 (0개의 아이디얼 점을 포함함)에 내접되는 것처럼 호로-구(horosphere)에 내접됩니다. 쌍곡선 타일링 자체가 칠각형 타일링 벌집(heptagonal tiling honeycomb) {7,3,3}에서와 같이 비-컴팩트 쌍곡선 테셀레이션의 패싯으로 사용될 때 순서열이 확장됩니다; 그것들은 2개의 아이디얼 점을 가지는 등거리 표면 (2-초원(hypercycle))에 내접됩니다.

Regular tilings of the real projective plane

정규 다면체의 또 다른 그룹은 실수 투영 평면(real projective plane)의 타일링으로 구성됩니다. 이것들은 반-입방체(hemi-cube), 반-팔면체(hemi-octahedron), 반-십이면체(hemi-dodecahedron), 및 반-이십면체(hemi-icosahedron)를 포함합니다. 그것들은 (전역적) 투영 다면체(projective polyhedra)이고, 플라톤 고체(Platonic solids)의 투영 짝입니다. 사면체는 다른 4개의 플라톤 고체처럼 식별될 수 있는 평행한 면의 쌍이 없기 때문에 투영 짝이 없습니다.

Hemi-cube {4,3}	Hemi-octahedron {3,4}	Hemi-dodecahedron {3,5}	Hemi-icosahedron {5,3}

이들은 원래 플라톤 고체와 같은 방법으로 이중 쌍으로 발생합니다. 그것들의 오일러 특성은 모두 1입니다.

Abstract regular polyhedra

지금까지, 다면체는 차원의 임의의 숫자에서 더 일반적인 폴리토프(polytopes)의 3-차원 예제라고 굳게 이해되었습니다. 20세기 후반에는 다면체 조합론(Polyhedral combinatorics)과 같은 추상적인 대수적 아이디어가 발전했으며, 원소의 부분적으로 순서화된 집합(partially ordered set, 포셋)으로 추상적인 폴리토프(abstract polytope)라는 아이디어가 절정에 이르렀습니다. 추상 다면체의 원소는 몸체 (최대 원소), 면, 가장자리, 꼭짓점 및 널 폴리토프(null polytope) 또는 빈 집합입니다. 이들 추상적 원소는 보통의 공간에 매핑되거나 기하학적 도형으로 구현될 수 있습니다. 일부 추상 다면체는 잘-형성되거나 충실한 구현을 가지고 있지만, 다른 것들은 그렇지 않습니다. 플래그(flag)는 몸체, 면, 면의 가장자리, 가장자리의 꼭짓점, 및 널 폴리토프인 다면체에 대해 각 차원의 원소의 연결된 집합입니다. 추상적 폴리포트는 그것의 조합론적 대칭이 그것의 깃발에 전이적이라면 정규라고 말합니다 – 다시 말해서, 임의의 플래그는 다면체의 대칭 아래에서 임의의 다른 플래그에 매핑될 수 있습니다. 추상적 정규 폴리토프는 여전히 활발하게 연구되는 분야로 남아 있습니다.

충실하게 구현될 수 없는 5개의 그러한 정규 추상 다면체는 H. S. M. Coxeter에 의해 그의 저서 Regular Polytopes (1977)에서, 그리고 다시 J. M. Wills에 의한 그의 논문 "The combinatorially regular polyhedra of index 2" (1987)에서 식별되었습니다. 다섯 가지 모두는 C₂×S₅ 대칭을 가지지만 대칭의 절반, 즉, C₂×A₅ 또는 이십면체 대칭으로만 구현될 수 있습니다.^[9]^[10]^[11] 그것들은 모두 토로이드(toroids)와 토폴로지적으로 동등합니다. 각 꼭짓점 주위에 n개의 면을 배열함으로써 그것들의 구성은 쌍곡형 평면(hyperbolic plane)의 타일링으로 무한하게 반복될 수 있습니다. 아래 다이어그램에서, 쌍곡형 타일링 이미지는 다면체 이미지의 색상에 해당하는 색상을 가집니다.

Polyhedron	Medial rhombic triacontahedron	Dodecadodecahedron	Medial triambic icosahedron	Ditrigonal dodecadodecahedron	Excavated dodecahedron
Type	Dual {5,4}₆	{5,4}₆	Dual of {5,6}₄	{5,6}₄	{6,6}₆
(v,e,f)	(24,60,30)	(30,60,24)	(24,60,20)	(20,60,24)	(20,60,20)
Vertex figure	{5}, {5/2}	(5.5/2)²	{5}, {5/2}	(5.5/3)³
Faces	30 rhombi	12 pentagons 12 pentagrams	20 hexagons	12 pentagons 12 pentagrams	20 hexagrams
Tiling	{4, 5}	{5, 4}	{6, 5}	{5, 6}	{6, 6}
χ	−6	−6	−16	−16	−20

Petrie dual

정규 다면체의 피트리 이중(Petrie dual)은 꼭짓점과 가장자리가 원래 다면체의 꼭짓점과 가장자리에 해당하고, 면이 꼬인 피트리 다각형(Petrie polygons)의 집합인 정규 맵(regular map)입니다.^[12]

Regular petrials
Name	Petrial tetrahedron	Petrial cube	Petrial octahedron	Petrial dodecahedron	Petrial icosahedron
Symbol	{3,3}^$π$	{4,3}^$π$	{3,4}^$π$	{5,3}^$π$	{3,5}^$π$
(v,e,f), χ	(4,6,3), χ = 1	(8,12,4), χ = 0	(6,12,4), χ = −2	(20,30,6), χ = −4	(12,30,6), χ = −12
Faces	3 skew squares	4 skew hexagons		6 skew decagons
Faces	3 skew squares
Image
Animation
Related figures	{4,3}₃ = {4,3}/2 = {4,3}_(2,0)	{6,3}₃ = {6,3}_(2,0)	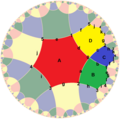{6,4}₃ = {6,4}_(4,0)	{10,3}₅	{10,5}₃

Spherical polyhedra

보통의 5개의 정규 다면체는 구형 타일링 (구의 타일링)으로도 나타낼 수 있습니다:

Tetrahedron {3,3}	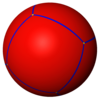Cube {4,3}	Octahedron {3,4}	Dodecahedron {5,3}	Icosahedron {3,5}

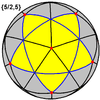Small stellated dodecahedron {5/2,5}	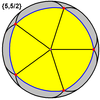Great dodecahedron {5,5/2}	Great stellated dodecahedron {5/2,3}	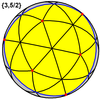Great icosahedron {3,5/2}

Regular polyhedra that can only exist as spherical polyhedra

슐래플리 기호가 {m, n}인 정규 다면체에 대해, 다각형 면의 개수는 다음과 같이 구할 수 있습니다:

N_{2}={\frac {4n}{2m+2n-mn}}

고대에 알려진 플라톤 고체(Platonic solids)는 m ≥ 3과 n ≥ 3에 대한 유일한 정수 해입니다. 제한 m ≥ 3은 다각형 면이 적어도 3개의 면을 가져야 한다는 것을 강제합니다.

다면체를 구형 타일링(spherical tiling)으로 고려할 때, 2각형(digons)이 비-영 넓이를 가지는 구형 달로 표현될 수 있기 때문에 이 제한이 완화될 수 있습니다. m = 2를 허용하면 호소헤드라(hosohedra)인 정규 다면체의 새로운 무한 클래스를 허용합니다. 구형 표면에서, 정규 다면체 {2, n}은 2 $π$ /n의 내부 각도를 갖는 n에 인접한 달로 표시됩니다. 모든 이들 달은 두 개의 공통 꼭짓점을 공유합니다.^[13]

3차원 유클리드 공간에서 정규 이면체 {n, 2}는^[13] 결과 대상이 두 개의 선분으로 이각형을 구성할 수 있는 것과 유사하게 깊이를 가지지 않도록 "뒤에서-뒤로" 연결된 두 개의 (평면) n-변 다각형(polygons)으로 구성된 퇴화 각기둥(prism)으로 고려될 수 있습니다. 어쨌든, 구형 타일링(spherical tiling)으로서, 이면체는 두 개의 n-측면 면이 구를 덮고, 각 면이 반구(hemisphere)이고, 꼭짓점이 큰 원(great circle)을 중심으로 하는 비-퇴화 형식으로 존재할 수 있습니다. 그것은 꼭짓점이 같게 간격을 유지하면 정규입니다.

Digonal dihedron {2,2}	Trigonal dihedron {3,2}	Square dihedron {4,2}	Pentagonal dihedron {5,2}	Hexagonal dihedron {6,2}	...	{n,2}
Digonal hosohedron {2,2}	Trigonal hosohedron {2,3}	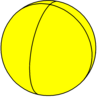Square hosohedron {2,4}	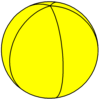Pentagonal hosohedron {2,5}	Hexagonal hosohedron {2,6}	...	{2,n}

호소헤드론 {2,n}은 이면체 {n,2}에 대한 이중입니다. n = 2일 때, 호소헤드론이자 이면체인 다면체 {2,2}를 얻습니다. 이것들은 모두 오일러 특성 2를 가집니다.

References

^ Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 77. ISBN 0-521-66405-5.
^ Chen, Zhibo, and Liang, Tian. "The converse of Viviani's theorem", The College Mathematics Journal 37(5), 2006, pp. 390–391.
^ The Scottish Solids Hoax.
^ Hagino, K., Onuma, R., Kawachi, M. and Horiguchi, T. (2013) "Discovery of an endosymbiotic nitrogen-fixing cyanobacterium UCYN-A in Braarudosphaera bigelowii (Prymnesiophyceae)". PLoS One, 8(12): e81749. doi:10.1371/journal.pone.0081749.
^ ^a ^b Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6. Online version at Kurt Stüber's Biolib (in german)
^ "Myoviridae". Virus Taxonomy. Elsevier. 2012. pp. 46–62. doi:10.1016/b978-0-12-384684-6.00002-1. ISBN 9780123846846.
^ STRAUSS, JAMES H.; STRAUSS, ELLEN G. (2008). "The Structure of Viruses". Viruses and Human Disease. Elsevier. pp. 35–62. doi:10.1016/b978-0-12-373741-0.50005-2. ISBN 9780123737410. S2CID 80803624.
^ Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
^ The Regular Polyhedra (of index two), David A. Richter
^ Regular Polyhedra of Index Two, I Anthony M. Cutler, Egon Schulte, 2010
^ Regular Polyhedra of Index Two, II Beitrage zur Algebra und Geometrie 52(2):357–387 · November 2010, Table 3, p.27
^ McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge University Press, p. 192, ISBN 9780521814966
^ ^a ^b Coxeter, Regular polytopes, p. 12

Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
'there are 48 regular polyhedra' jan Misali

External links

Weisstein, Eric W. "Regular Polyhedron". MathWorld.

[1] Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 77. ISBN 0-521-66405-5.

[2] Chen, Zhibo, and Liang, Tian. "The converse of Viviani's theorem", The College Mathematics Journal 37(5), 2006, pp. 390–391.

[3] The Scottish Solids Hoax.

[Hagino2013-4] Hagino, K., Onuma, R., Kawachi, M. and Horiguchi, T. (2013) "Discovery of an endosymbiotic nitrogen-fixing cyanobacterium UCYN-A in Braarudosphaera bigelowii (Prymnesiophyceae)". PLoS One, 8(12): e81749. doi:10.1371/journal.pone.0081749.

[Haeckel1904-5] Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6. Online version at Kurt Stüber's Biolib (in german)

[6] "Myoviridae". Virus Taxonomy. Elsevier. 2012. pp. 46–62. doi:10.1016/b978-0-12-384684-6.00002-1. ISBN 9780123846846.

[7] STRAUSS, JAMES H.; STRAUSS, ELLEN G. (2008). "The Structure of Viruses". Viruses and Human Disease. Elsevier. pp. 35–62. doi:10.1016/b978-0-12-373741-0.50005-2. ISBN 9780123737410. S2CID 80803624.

[8] Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)

[9] The Regular Polyhedra (of index two), David A. Richter

[10] Regular Polyhedra of Index Two, I Anthony M. Cutler, Egon Schulte, 2010

[11] Regular Polyhedra of Index Two, II Beitrage zur Algebra und Geometrie 52(2):357–387 · November 2010, Table 3, p.27

[12] McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge University Press, p. 192, ISBN 9780521814966

[cox-13] Coxeter, Regular polytopes, p. 12

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]