Prism (geometry)

Set of uniform $n$ -gonal prisms
Set of uniform n-gonal prisms
	Example uniform hexagonal prism
Type	uniform in the sense of semiregular polyhedron
Faces	2 n-gonal regular polygons; n squares
Edges	3n
Vertices	2n
Vertex configuration	4.4.n
Schläfli symbol	{n}×{} ; t{2, n}
Conway notation	Pn
Coxeter diagram
Symmetry group	Dnh, [n,2], (*n22), order 4n
Rotation group	Dn, [n,2]+, (n22), order 2n
Dual polyhedron	convex dual-uniform n-gonal bipyramid
Properties	convex, regular polygon faces, vertex-transitive, translated bases, sides ⊥ bases
Net

기하학(geometry)에서, 각기둥(prism)은 n-변 다각형 밑면)(base), 첫 번째 밑면의 평행이동된(translated) 복사본 (회전없이 단단하게 이동)인 두 번째 밑면, 및 두 밑면의 대응하는 변(corresponding sides)을 연결하는 n 개의 다른 면(faces), 필연적으로 모두 평행사변형(parallelograms)으로 구성된 다면체(polyhedron)입니다. 밑면에 평행한 모든 교차-단면(cross-sections)은 밑면의 평행이동입니다. 각기둥은 그것의 밑면의 이름을 따서 지어집니다. 예를 들어 오각형(pentagonal) 밑면을 갖는 각기둥은 오각형 각기둥이라고 합니다. 각기둥은 각기둥형(prismatoids)의 부분클래스입니다.

많은 기본 기하학 용어와 마찬가지로, prism이라는 단어 (from el πρίσμα (prisma), meaning 'something sawed')는 유클리드의 원론(Euclid's Elements)에서 처음 사용되었습니다. 유클리드는 책 XI에서 그 용어를 "두 개의 반대 편에 있고, 같고 평행한 평면으로 구성된 고체 도형이지만, 나머지는 평행사변형"으로 정의했습니다. 어쨌든, 이 정의는 밑면의 본성과 관련하여 충분히 구체적이지 않다는 비판을 받아 이후 기하학 작가들 사이에서 혼란을 야기했습니다.^[2]^[3]

Oblique prism

경사진 각기둥은 결합하는 가장자리와 면이 밑면 면에 수직(perpendicular)이 아닌 각기둥입니다.

예제: 평행-육면체형(parallelepiped)은 그 밑면이 평행사변형인 경사진 각기둥이거나, 동등하게 모두 평행사변형인 6개의 면을 갖는 다면체입니다.

Right prism, uniform prism

Right prism

직각 각기둥은 결합하는 가장자리와 면이 밑면 면에 수직(perpendicular)인 각기둥입니다.^[4] 이것은 모든 결합하는 면이 직사각형(rectangular)인 경우에 적용됩니다.

직각 n-각기둥의 이중(dual)은 직각 n-쌍각뿔(bipyramid)입니다.

정규 n-각형(regular n-gon) 밑면을 갖는 (직사각형 변을 갖는) 직각 각기둥은 Schläfli 기호 { }×{n}를 가집니다. 그것은 n이 무한대(infinity)에 접근함에 따라 원통형(cylindrical) 고체에 접근합니다. 실린더는 원형 프리즘으로 간주됩니다.

Special cases

직각 직사각형 각기둥 (직사각형 밑면을 가짐)은 직육면체형(cuboid) 또는 비공식적으로 직사각형 상자라고도 합니다. 직각 직사각형 각기둥 Schläfli 기호 { }×{ }×{ }를 가집니다.

직각 정사각 각기둥 (정사각형 밑면을 가짐)은 정사각형 직육면체형 또는 비공식적으로 정사각형 상자라고도 합니다.

참고: 일부 텍스트에서는 직사각형 각기둥 또는 정사각 각기둥이라는 용어를 직각 직사각형-밑면 각기둥과 직각 정사각형-밑면 각기둥 모두에 적용할 수 있습니다.

Uniform prism

균등 각기둥(uniform prism) 또는 반정규 각기둥(semiregular prism)은 그러한 각기둥이 균등 다면체(uniform polyhedra)의 집합 내에 있기 때문에 정규(regular) 밑변과 정사각형(square) 변을 갖는 직각 각기둥입니다.

균등 n-각형 각기둥은 Schläfli 기호 t{2,n}을 가집니다.

정규 밑면과 같은 가장자리 길이를 갖는 직각 각기둥은 두 개의 무한 수열의 반정규 다면체(semiregular polyhedra) 중 하나를 형성하고, 나머지 하나의 급수는 역각기둥(antiprisms)입니다.

Family of uniform n-gonal prisms v t e
Prism name	Digonal prism	(Trigonal) Triangular prism	(Tetragonal) Square prism	Pentagonal prism	Hexagonal prism	Heptagonal prism	Octagonal prism	Enneagonal prism	Decagonal prism	Hendecagonal prism	Dodecagonal prism	...	Apeirogonal prism
Polyhedron image												...
Spherical tiling image												Plane tiling image
Vertex config.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diagram												...

Volume

각기둥의 부피(volume)는 밑면의 넓이(area)와 두 밑면 면 사이의 거리, 또는 높이의 곱입니다 (비-직각 각기둥의 경우에서, 이것은 수직 거리를 의미함에 주목하십시오).

그 부피는 따라서 다음과 같습니다:

V=Bh

여기서 B는 밑면 넓이이고 h는 높이입니다. 그것의 밑면이 변 길이 s를 갖는 n-변 정규 다각형(regular polygon)인 각기둥의 부피는 따라서 다음과 같습니다:

V={\frac {n}{4}}hs^{2}\cot \left({\frac {\pi }{n}}\right)

Surface area

직각 각기둥의 표면 넓이(area)는 다음과 같습니다:

2B+Ph

여기서 B는 밑면의 넓이, h는 높이이고, P는 밑면 둘레(perimeter)입니다.

그것의 밑면이 변 길이 s와 높이 h를 갖는 정규 n-변 다각형(polygon)인 직각 각기둥의 표면 넓이는 따라서 다음입니다:

A={\frac {n}{2}}s^{2}\cot {\left({\frac {\pi }{n}}\right)}+nsh

Schlegel diagrams

P3	P4	P5	P6	P7	P8

Symmetry

정규 밑면을 갖는 직각 n-면 각기둥의 대칭 그룹(symmetry group)은 차수 4n의 D_nh입니다. 단, 부분그룹(subgroups)으로 D_4h의 세 가지 버전을 가지는 차수 48의 더 큰 대칭 그룹 O_h를 가지는 정육면체의 경우는 예외입니다. 회전 그룹(rotation group)은 차수 2n의 D_n입니다. 단, 부분그룹으로 D₄의 세 가지 버전을 가지는 차수 24차의 더 큰 대칭 그룹 O를 가지는 정육면체의 경우는 예외입니다.

대칭 그룹 D_nh이 반전(inversion)을 포함하는 것과 n이 짝수인 것은 필요충분(iff) 조건입니다.

호소헤드라(hosohedra)와 다이히드라(dihedra)도 이면체 대칭성을 보유하고, n-각형 각기둥은 n-각형 호소헤드라의 기하학적 절단(geometrical truncation)과 마찬가지로 n-각형 이면체의 캔틀레이션(cantellation) 또는 확장(expansion)을 통해 구성될 수 있습니다.

Truncated prism

잘린 각기둥(truncated prism)은 비-평행(parallel) 윗면과 아랫면을 갖는 각기둥입니다.^[5]

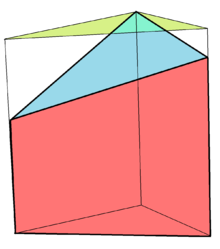
Example truncated triangular prism. Its top face is truncated at an oblique angle, but it is NOT an oblique prism!

Twisted prism

꼬인 각기둥(twisted prism)은 각 측면이 정사각형 대각선으로 이등분된 균등 n-각기둥으로 구성된 비볼록 다면체로, 보통 같은 방향으로 $π$ /n 라디안 (180/n 도)만큼 윗면을 비틀어서 측면을 오목하게 만듭니다.^[6]^[7]

꼬인 각기둥은 새로운 꼭짓점 추가하지 않고 사면체로 해부(dissected)될 수 없습니다. 가장 작은 경우: 삼각형 형태는 쇤하르트 다면체(Schönhardt polyhedron)라고 합니다.

n-각형 꼬인 각기둥은 토폴로지적으로 n-각형 균등 역각기둥(antiprism)과 동일하지만, 대칭 그룹(symmetry group)의 절반: D_n, [n,2]⁺, 차수 2n을 가집니다. 그것은 삼각형 쌍 사이에서 제거된 사면체를 갖는 비볼록 역각기둥으로 보일 수 있습니다.

3-gonal	4-gonal		12-gonal
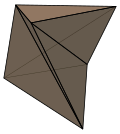Schönhardt polyhedron	Twisted square prism	Square antiprism	Twisted dodecagonal antiprism

Frustum

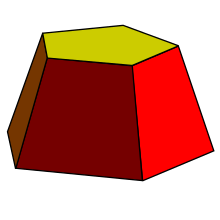
절두체(frustum)는 사다리꼴(trapezoid) 측면과 서로 다른 크기의 윗면과 밑면 다각형을 갖는 각기둥과 유사한 구조입니다.

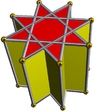
Star prism

별 각기둥(star prism)은 위쪽과 아래쪽에 두 개의 같은 별 다각형(star polygon) 면으로 구성된 비-볼록 다면체로, 두 면은 평행하고 거리만큼 오프셋되고 직사각형 면에 의해 연결됩니다. 균등 별 각기둥은 슐래플리 기호(Schläfli symbol) {p/q} × { }를 가지며, p 직사각형과 2 {p/q} 면을 가집니다. 그것은 위상학적으로 p-각형 각기둥과 동일합니다.

Examples
{ }×{ }₁₈₀×{ }	t_a{3}×{ }		{5/2}×{ }	{7/2}×{ }	{7/3}×{ }	{8/3}×{ }
D_2h, order 8	D_3h, order 12		D_5h, order 20	D_7h, order 28		D_8h, order 32

Crossed prism

교차 각기둥(crossed prism)은 각기둥으로 구성된 비볼록 다면체로, 여기서 한 밑면의 꼭짓점들이 이 밑면의 중심을 중심으로 반전 (또는 180° 회전)됩니다. 이것은 측면 직사각형 면을 교차 직사각형(crossed rectangles)으로 변환합니다. 정규 다각형 밑면에 대해, 그 모양은 n-각형 모래시계(hour glass)입니다. 모든 경사 가장자리는 단일 몸체 중심을 통과합니다. 참고: 이 몸체 중심에는 꼭짓점이 없습니다. 교차 각기둥은 토폴로지적으로 n-각형 각기둥과 동일합니다.

Examples
{ }×{ }₁₈₀×{ }₁₈₀	t_a{3}×{ }₁₈₀		{3}×{ }₁₈₀	{4}×{ }₁₈₀	{5}×{ }₁₈₀	{5/2}×{ }₁₈₀	{6}×{ }₁₈₀
D_2h, order 8	D_3d, order 12			D_4h, order 16	D_5d, order 20		D_6d, order 24

Toroidal prism

토러스적 각기둥(toroidal prism)은 교차 프리즘과 같은 비-볼록 다면체이지만, 밑면과 윗면이 없고, 다면체를 닫는 단순한 직사각형 측면을 가집니다. 이것은 짝수-변 밑변 다각형에 대해서만 수행될 수 있습니다. 이것들은 영의 오일러 특성(Euler characteristic)을 갖는 토폴로지 토러스입니다. 토폴로지적 다면체 전개도(polyhedral net)는 (꼭짓점 구성(ertex configuration) 4.4.4.4를 갖는) 정사각형 타일링의 두 개의 행: n 정사각형의 밴드, 각각 교차 직사각형(crossed rectangle)에 부착된 것에서 잘라낼 수 있습니다. n-각형 토로이드 각기둥은 2n개의 꼭짓점, 2n개의 면: n개의 정사각형과 n개의 교차 직사각형, 및 4n개의 가장자리를 가지고 있습니다. 그것은 토폴로지적으로 자기-이중(self-dual)입니다.

Examples
D_4h, order 16	D_6h, order 24
v=8, e=16, f=8	v=12, e=24, f=12

Prismatic polytope

각기둥 폴리토프(polytope)는 각기둥의 고차원 일반화입니다. n-차원 각기둥 폴리토프는 두 개의 (n − 1)-차원 폴리토프로 구성되어, 다음 차원으로 평행이동됩니다.

각기둥 n-폴리토프 원소는 (n − 1)-폴리토프 원소에서 두 배되고 그런-다음 다음 하위 원소에서 새 원소를 만듭니다.

f_i i-면 원소 (i = 0, ..., n)를 갖는 n-폴리토프를 취하십시오. 그것의 (n + 1)-폴리토프 각기둥은 2f_i + f_i−1 i-면 원소를 가질 것입니다. (f₋₁ = 0, f_n = 1일 때.)

차원에 의해:

n 꼭짓점과 n 가장자리를 갖는 다각형(polygon)을 취하십시오. 그것의 각기둥은 2n 꼭짓점, 3n 가장자리, 2 + n 면을 가지고 있습니다.
v 꼭짓점, e 가장자리, 및 f 면을 갖는 다면체(polyhedron)를 취하십시오. 그것의 각기둥은 2v 꼭짓점, 2e + v 가장지리, 2f + e 면, 및 2 + f 셀을 가지고 있습니다.
v 꼭짓점, e 가장자리, f 면, 및 c 셀을 갖는 폴리코론(polychoron)를 취하십시오. 그것의 각기둥은 2v 꼭짓점, 2e + v 가장자리, 2f + e 면, 2c + f 셀, 및 2 + c 초셀을 가지고 있습니다.

Uniform prismatic polytope

슐래플리 기호(Schläfli symbol) {p, q, ..., t}에 의해 표시되는 정규 n-폴리토프는 둘의 슐래플리 기호(Schläfli symbol)의 데카르트 곱(Cartesian product): {p, q, ..., t}×{}에 의해 표현되는 균등 각기둥 (n + 1)-폴리토프를 형성할 수 있습니다.