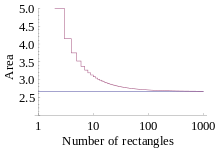
Riemann sum

Original article: w:Riemann sum

Four of the Riemann summation methods for approximating the area under curves. Right and left methods make the approximation using the right and left endpoints of each subinterval, respectively. Maximum and minimum methods make the approximation using the largest and smallest endpoint values of each subinterval, respectively. The values of the sums converge as the subintervals halve from top-left to bottom-right.

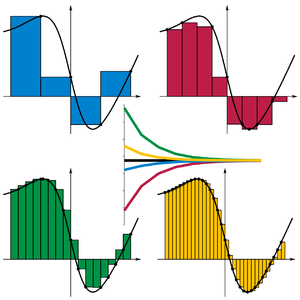
수학(mathematics)에서, 리만 합은 유한 합에 의한 적분의 특정 종류의 근사(approximation)입니다. 그것은 19세기 독일 수학자 베른하르트 리만(Bernhard Riemann)의 이름을 따서 지어졌습니다. 하나의 매우 공통적인 응용은 그래프 위의 함수 또는 직선의 넓이를 근사화하는 것이지만, 역시 곡선의 길이를 근사화하고 다른 근사가 있습니다.

합은 측정된 영역과 유사한 영역을 함께 형성하는 모양 (직사각형(rectangle), 사다리꼴(trapezoid), 포물선(parabola), 또는 삼차(cubics))으로 영역을 분할(partitioning)하고, 그런-다음 이들 각 모양에 대해 넓이를 계산하고, 마지막으로 이들 작은 넓이 모두를 함께 더함으로써 계산됩니다. 이 접근 방식은 심지어 미적분학의 기본 정리(fundamental theorem of calculus)가 닫힌-형식 해(closed-form solution)를 쉽게 찾도록 만들지 못하더라도 한정 적분(definite integral)에 대한 수치적 근사를 찾기 위해 사용될 수 있습니다.

작은 모양에 의해 채워진 영역은 보통 측정된 영역과 정확하게 같은 모양은 아니기 때문에, 리만 합은 측정된 넓이와 다를 것입니다. 이 오차는 점점 더 작은 모양을 사용하여 영역을 더 미세하게 분할함으로써 줄어들 수 있습니다. 모양이 점점 작아질수록, 그 합은 리만 적분(Riemann integral)에 접근합니다.

Definition

$f:[a,b]\rightarrow \mathbb {R}$를 실수 $\mathbb {R}$의 닫힌 구간(closed interval) $[a,b]$ 위에 정의된 함수로 놓고 다음을 I의 분할로 놓습니다:

$P=\left\{[x_{0},x_{1}],[x_{1},x_{2}],\dots ,[x_{n-1},x_{n}]\right\}$.

여기서,

$a=x_{0}<x_{1}<x_{2}<\cdots <x_{n}=b$.

분할 P를 갖는 I에 걸쳐 f의 리만 합 $S$는 다음으로 정의됩니다:

$S=\sum _{i=1}^{n}f(x_{i}^{*})\,\Delta x_{i}$

여기서 $\Delta x_{i}=x_{i}-x_{i-1}$이고 $x_{i}^{*}\in [x_{i-1},x_{i}]$입니다. 우리가 어떤 $x_{i}^{*}$들이 선택되었는지에 따라 다른 리만 합을 생성할 수 있습니다. 만약 그 함수가 리만 적분가능(Riemann integrable)이면, 더해지는 숫자의 차이 또는 너비 $\Delta x_{i}$가 0에 접근할 때, 결국 이것은 문제가 되지 않을 것입니다.

Some specific types of Riemann sums

특정 $x_{i}^{*}$의 선택은 리만 합의 다른 유형을 제공합니다:

• 만약 모든 i에 대해 $x_{i}^{*}=x_{i-1}$이면, S는 왼쪽 규칙 또는 왼쪽 리만 합이라고 불립니다.
• 만약 모든 i에 대해 $x_{i}^{*}=x_{i}$이면, S는 오른쪽 규칙 또는 오른쪽 리만 합이라고 불립니다.
• 만약 모든 i에 대해 $x_{i}^{*}=(x_{i}+x_{i-1})/2$이면, S는 중간점 규칙 또는 중간 리만 합이라고 불립니다.
• 만약 $f(x_{i}^{*})=\sup f([x_{i-1},x_{i}])$ (즉, $[x_{i-1},x_{i}]$에 걸쳐 f의 상한(supremum))이면, S는 위쪽 리만 합 또는 위쪽 다르부 합으로 정의됩니다.
• 만약 $f(x_{i}^{*})=\inf f([x_{i-1},x_{i}])$ (즉, $[x_{i-1},x_{i}]$에 걸쳐 f의 하한(infimum))이면, S는 아래쪽 리만 합 또는 아래쪽 다르부 합으로 정의됩니다.

모든 이들 방법은 수치적 적분(numerical integration)을 수행하는 가장 기본적인 방법 중 하나입니다. 느슨하게 말해서, 만약 분할이 "점점 더 미세해짐"에 따라 모든 리만 합이 수렴하면 함수는 리만 적분가능(Riemann integrable)입니다.

리만 합으로 파생되지는 않았지만, 왼쪽과 오른쪽 리만 합의 평균은 사다리꼴 합(trapezoidal sum)이고 가중된 평균을 사용하여 적분을 근사하는 가장 일반적인 방법 중 하나입니다. 이것은 심슨의 규칙(Simpson's rule)과 뉴턴–코츠 공식(Newton–Cotes formulas)이 복잡성에서 뒤따릅니다.

주어진 분할 위에 임의의 리만 합 (즉, $x_{i-1}$와 $x_{i}$ 사이의 $x_{i}^{*}$의 임의의 선택에 대해)은 아래쪽과 위쪽 다르부 합 사이에 포함됩니다. 이것은 궁극적으로 리만 적분과 동등한 것인 다르부 적분(Darboux integral)의 기초를 형성합니다.

Methods

리만 합의 네 가지 방법은 보통 같은 크기의 분할과 함께 가장 좋게 접근됩니다. 구간 [a, b]는 따라서 $n$ 부분구간, 각각 다음 길이로 나뉩니다:

$\Delta x={\frac {b-a}{n}}.$

분할에서 점은 그때에 다음일 것입니다:

$a,\;a+\Delta x,\;a+2\Delta x,\;\ldots ,\;a+(n-2)\Delta x,\;a+(n-1)\Delta x,\;b.$

Left Riemann sum

Left Riemann sum of x³ over [0,2] using 4 subdivisions

왼쪽 리만 합에 대해, 왼쪽-끝 점에서 그것의 값에 의해 함수를 근사화하는 것은 밑변 Δx와 높이 f(a + iΔx)를 갖는 다수의 직사각형을 제공합니다. i = 0, 1, …, n − 1에 대해 이것을 하고, 결과 넓이를 더함으로써 다음을 제공합니다:

$A_{\mathrm {left} }=\Delta x\left[f(a)+f(a+\Delta x)+f(a+2\,\Delta x)+\cdots +f(b-\Delta x)\right].$

왼쪽 리만 합은 만약 f가 이 구간 위에 단조 감소(monotonically decreasing)하는 것이면 과대평가되고, 그것이 단조 증가(monotonically increasing)하는 것이면 과소평가됩니다.

Right Riemann sum

Right Riemann sum of x³ over [0,2] using 4 subdivisions

f는 여기서 오른쪽 끝점에서 값에 의해 근사화됩니다. 이것은 밑변 Δx와 높이 f(a + i Δx)를 갖는 다수의 직사각형을 제공합니다. i = 1, …, n에 대해 이것을 하고, 결과 넓이를 더함으로써 다음을 제공합니다:

$A_{\mathrm {right} }=\Delta x\left[f(a+\Delta x)+f(a+2\,\Delta x)+\cdots +f(b)\right].$

오른쪽 리만 합은 만약 f가 이 구간 위에 단조 감소(monotonically decreasing)하는 것이면 과소평가되고, 그것이 단조 증가(monotonically increasing)하는 것이면 과대평가됩니다. 이 공식의 오차는 다음일 것입니다:

$\left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {right} }\right\vert \leq {\frac {M_{1}(b-a)^{2}}{2n}}$,

여기서 $M_{1}$은 구간 위의 $f^{\prime }(x)$의 절댓값(absolute value)의 최댓값입니다.

Midpoint rule

Midpoint Riemann sum of x³ over [0,2] using 4 subdivisions

구간의 중간점에서 f를 근사화하는 것은 첫 번째 구간에 대해 f(a + Δx/2), 다음에 대해 f(a + 3Δx/2), 및 이런 식으로 f(b − Δx/2)까지 제공합니다. 넓이를 더함으로써 다음을 제공합니다:

$A_{\mathrm {mid} }=\Delta x\left[f\left(a+{\tfrac {\Delta x}{2}}\right)+f\left(a+{\tfrac {3\,\Delta x}{2}}\right)+\cdots +f\left(b-{\tfrac {\Delta x}{2}}\right)\right]$.

이 공식의 오차는 다음일 것입니다:

$\left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {mid} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{24n^{2}}}$,

여기서 $M_{2}$는 구간 위의 $f^{\prime \prime }(x)$의 절댓값(absolute value)의 최댓값입니다.

Trapezoidal rule

Trapezoidal Riemann sum of x³ over [0,2] using 4 subdivisions

Main article: Trapezoidal rule

이 경우에서, 구간 위에 함수 f의 값은 왼쪽과 오른쪽 끝점에서 값의 평균에 의해 근사화됩니다. 위와 같은 방식에서, 평행 변 b₁, b₂와 높이 h를 갖는 사다리꼴(trapezium)에 대해 다음 넓이 공식을 사용하여 간단한 계산은

$A={\tfrac {1}{2}}h(b_{1}+b_{2})$

다음을 제공합니다:

$A_{\mathrm {trap} }={\tfrac {1}{2}}\,\Delta x\left[f(a)+2f(a+\Delta x)+2f(a+2\,\Delta x)+\cdots +f(b)\right].$

이 공식의 오차는 다음일 것입니다:

$\left\vert \int _{a}^{b}f(x)\,dx-A_{\mathrm {trap} }\right\vert \leq {\frac {M_{2}(b-a)^{3}}{12n^{2}}},$

여기서 $M_{2}$는 $f^{\prime \prime }(x)$의 절댓값의 최댓값입니다.

함수에 대해 사다리꼴 규칙으로 얻어진 근삿값은 해당 함수의 왼쪽과 오른쪽 합의 평균과 같습니다.

Connection with integration

도메인 $[a,b]$에 걸쳐 일-차원 리만 합에 대해, 분할 원소의 최대 크기가 영으로 축소됨에 따라 (즉, 분할의 노름의 극한이 영으로 감), 일부 함수는 같은 값으로 수렴하는 모든 리만 합을 가질 것입니다. 이 극한하는 값은, 만약 그것이 존재하면, 도메인에 걸쳐 함수의 리만 한정 적분으로 정의됩니다:

$\int _{a}^{b}\!f(x)\,dx=\lim _{\|\Delta x\|\rightarrow 0}\sum _{i=1}^{n}f(x_{i}^{*})\,\Delta x_{i}.$

유한-크기 도메인에 대해, 만약 분할 원소의 최대 크기가 영으로 줄어들면, 이것은 분할 원소의 숫자가 무한대로 감을 의미합니다. 유한 분할에 대해, 리만 합은 항상 극한하는 값에 대한 근삿값이고 이 근사는 분할이 더 미세할수록 더 좋아집니다. 다음 애니메이션은 분할의 숫자를 늘리면서 (최대 분할 원소 크기를 낮추면서) 곡선 아래의 "넓이"를 더 잘 근사하는 방법을 보여줍니다:

• 
  Left sum
• 
  Right sum
• 
  Middle sum

여기에서 빨간색 함수는 매끄러운 함수로 가정되기 때문에, 모든 셋의 리만 합은 분할의 숫자가 무한대로 갈 때 같은 값으로 수렴할 것입니다.

Example

Comparison of right hand sums of the function y = x² from 0 to 2 with the integral of it from 0 to 2.

A visual representation of the area under the curve y = x² for the interval from 0 to 2. Using antiderivatives this area is exactly 8/3.

Approximating the area under $y=x^{2}$ from 0 to 2 using right-rule sums. Notice that because the function is monotonically increasing, right-hand sums will always overestimate the area contributed by each term in the sum (and do so maximally).

The value of the Riemann sum under the curve y = x² from 0 to 2. As the number of rectangles increases, it approaches the exact area of 8/3.

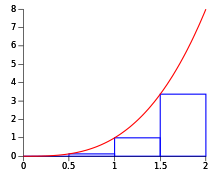
예제를 취하여, 0과 2 사이의 y = x² 곡선 아래의 넓이는 리만의 방법을 사용하여 절차적으로 계산될 수 있습니다.

구간 [0, 2]는 먼저 n 부분구간으로 나뉘며, 그것의 각각은 ${\tfrac {2}{n}}$의 너비로 주어집니다; 이것들은 리만 직사각형 (이하 "상자")의 너비입니다. 오른쪽 리만 합이 사용되어야 하기 때문에, 상자에 대해 x 좌표의 수열은 $x_{1},x_{2},\ldots ,x_{n}$일 것입니다. 그러므로, 상자의 높이의 수열은 $x_{1}^{2},x_{2}^{2},\ldots ,x_{n}^{2}$일 것입니다. 중요한 사실은 $x_{i}={\tfrac {2i}{n}}$이고, $x_{n}=2$라는 것입니다.

각 상자의 넓이는 ${\tfrac {2}{n}}\times x_{i}^{2}$일 것이고 따라서 n번째 오른쪽 리만 합은 다음일 것입니다:

${\begin{aligned}S&={\frac {2}{n}}\times \left({\frac {2}{n}}\right)^{2}+\cdots +{\frac {2}{n}}\times \left({\frac {2i}{n}}\right)^{2}+\cdots +{\frac {2}{n}}\times \left({\frac {2n}{n}}\right)^{2}\\&={\frac {8}{n^{3}}}\left(1+\cdots +i^{2}+\cdots +n^{2}\right)\\&={\frac {8}{n^{3}}}\left({\frac {n(n+1)(2n+1)}{6}}\right)\\&={\frac {8}{n^{3}}}\left({\frac {2n^{3}+3n^{2}+n}{6}}\right)\\&={\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\end{aligned}}$

만약 극한이 n → ∞일 때 보이면, 근사가 상자의 숫자가 증가함에 따라 곡선 아래의 넓이의 실제 값에 접근합니다. 따라서:

$\lim _{n\to \infty }S=\lim _{n\to \infty }\left({\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}\right)={\frac {8}{3}}$

이 방법은 보다 기계적인 방법에서 계산된 한정 적분과 일치합니다:

$\int _{0}^{2}x^{2}\,dx={\frac {8}{3}}$

함수가 구가 위에 연속적이고 단조적으로 증가하기 때문에, 오른쪽 리만 합은 적분을 가장 큰 총양에 의한 적분을 과대평가합니다 (반면에 왼쪽 리만 합은 가장 큰 총양에 의한 적분 과소평가합니다). 이 사실은, 다이어그램에서 직관적으로 명백해지고, 함수의 본성이 적분이 얼마나 정확하게 추정되는지를 결정하는 방법을 보여줍니다. 단순하지만, 오른쪽과 왼쪽 리만 합은 종종 사다리꼴 규칙(Trapezoidal rule) 또는 심슨의 규칙(Simpson's rule)과 같은 적분을 추정하는 고급 기술보다 정확도가 떨어집니다.

예제 함수는 찾기 쉬운 역도함수를 가지므로 리만 합에 의한 적분을 추정하는 것은 대부분 학문적 연습입니다; 어쨌든, 모든 함수가 역도함수를 가지는 것은 아니므로 합을 통해 적분을 추정하는 것이 실질적으로 중요하다는 점을 기억해야 합니다.

Higher dimensions

리만 합의 기본 아이디어는 분할을 통해 도메인을 조각으로 "나누고", 각 조각의 "크기"에 함수가 해당 조각에 취하는 값을 곱하고, 모든 이들 곱을 합하는 것입니다. 이것은 일 차원보다 많은 차원의 도메인에 걸쳐 함수에 대해 리만 합을 허용하기 위해 일반화될 수 있습니다.

직관적으로, 영역을 분할하는 과정은 이해하기 쉽지만, 영역이 분할될 수 있는 방법에 대한 기술적인 세부 사항은 일차원 경우보다 훨씬 더 복잡해지고 도메인의 기하학적 모양의 관점을 포함합니다.

Two dimensions

이차원에서, 도메인, $A$은 ${\textstyle A=\bigcup _{i}A_{i}}$를 만족하는 셀, $A_{i}$의 숫자로 나뉠 수 있습니다. 이차원에서, 각 셀은 그때에 $\Delta A_{i}$에 의해 표시되는 "넓이"를 가지는 것으로 해석될 수 있습니다. 리만 합은 다음입니다:

$S=\sum _{i=1}^{n}f(x_{i}^{*},y_{i}^{*})\,\Delta A_{i},$

여기서 $(x_{i}^{*},y_{i}^{*})\in A_{i}$입니다.

Three dimensions

삼차원에서, 분할 아래에서 ${\textstyle V=\bigcup _{i}V_{i}}$이고 $\Delta V_{i}$가 $i$에 의해 인덱스된 셀의 "부피"임을 만족하는 도메인에 대해 문자 $V$를 사용하는 것이 관례적입니다. 삼-차원 리만 합은 그때에 다음으로 쓸 수 있습니다:

$S=\sum _{i=1}^{n}f(x_{i}^{*},y_{i}^{*},z_{i}^{*})\,\Delta V_{i}$

여기서 $(x_{i}^{*},y_{i}^{*},z_{i}^{*})\in V_{i}$입니다.

Arbitrary number of dimensions

고차원 리만 합은 일차원에서 이차원으로, 이차원에서 삼차원으로와 유사함을 따릅니다. 임의적인 차원 n에 대해, 리만 합은 다음으로 쓸 수 있습니다:

$S=\sum _{i}f(P_{i}^{*})\,\Delta V_{i}$

여기서 $P_{i}^{*}\in V_{i}$, 즉, 그것은 n-차원 부피 $\Delta V_{i}$를 갖는 n-차원 셀 $V_{i}$에서 한 점입니다.

Generalization

높은 일반성에서, 리만 합은 다음으로 쓸 수 있습니다:

$S=\sum _{i}f(P_{i}^{*})\mu (V_{i})$

여기서 $P_{i}^{*}$는 분할 원소 $V_{i}$에 포함된 임의의 임의적인 점을 의미하고 $\mu$는 놓여있는 집합 위에 측정(measure)입니다. 대략적으로 말하자면, 측정은 집합의 "크기": 집합 $V_{i}$의 크기를 제공하는 함수입니다; 일차원에서, 이것은 종종 구간의 길이, 이차원에서 넓이, 삼차원에서, 부피로 해석될 수 있고, 이런 식으로 계속됩니다.

See also

• Antiderivative
• Euler method and midpoint method, related methods for solving differential equations
• Lebesgue integral
• Riemann integral, limit of Riemann sums as the partition becomes infinitely fine
• Simpson's rule, a powerful numerical method more powerful than basic Riemann sums or even the Trapezoidal rule
• Trapezoidal rule, numerical method based on the average of the left and right Riemann sum

External links

• Weisstein, Eric W. "Riemann Sum". MathWorld.
• A simulation showing the convergence of Riemann sums