3-dimensional coordinate system
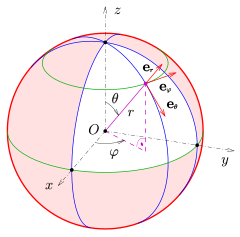
Spherical coordinates (r , θ , φ ) as commonly used in physics ISO 80000-2:2019 convention): radial distance r (distance to origin), polar angle θ (theta ) (angle with respect to polar axis), and azimuthal angle φ (phi ) (angle of rotation from the initial meridian plane). The symbol ρ (rho ) is often used instead of r . Spherical coordinates (r , θ , φ ) as often used in mathematics r , azimuthal angle θ , and polar angle φ . The meanings of θ and φ have been swapped compared to the physics convention. As in physics, ρ (rho ) is often used instead of r , to avoid confusion with the value r in cylindrical and 2D polar coordinates. A globe showing the radial distance, polar angle and azimuthal angle of a point P with respect to a unit sphere , in the mathematics convention. In this image, r equals 4/6, θ equals 90°, and φ equals 30°. 수학(mathematics) 에서, 구형 좌표 시스템 (spherical coordinate system )은, 점의 위치는 세 숫자: 고정된 원점으로부터 해당 점의 방사형 거리 (radial distance ), 고정된 천정(zenith) 방향으로부터 측정된 극 각도 (polar angle ), 및 원점을 통과하고 천정에 직각인 참조 평면 위의, 해당 평면 위의 고정된 참조 방향으로부터 측정된, 직각 투영 의 방위각 (azimuth angle )삼-차원 공간 에 대해 좌표 시스템(coordinate system) 입니다. 그것은 극좌표 시스템(polar coordinate system) 의 삼-차원 버전으로 볼 수 있습니다.
방사형 거리는 역시 반지름 (radius ) 또는 방사형 좌표 (radial coordinate )라고 불립니다. 극 각도는 공위도 (colatitude )천정 각도 (zenith angle )법선 각도 (normal angle )경사 각도 (inclination angle )
기호의 사용과 좌표의 순서는 출처와 분야에 따라 다릅니다. 이 가사는 물리학에서 빈번히 발생하는 ISO 관례를 사용합니다:[1]
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
(
ρ
,
θ
,
φ
)
{\displaystyle (\rho ,\theta ,\varphi )}
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
θ 와 φ 의 의미를 전환합니다. z- 축으로부터 반지름에 대해 r 과 같은 다른 관례도 사용되므로, 기호의 의미를 확인하려면 많은 주의를 기울여야 합니다.
지리적 좌표 시스템(geographical coordinate system) 의 관례에 따라, 위치는 위도, 경도, 및 높이 (고도)에 의해 측정됩니다. 서로 다른 토대 평면(fundamental planes) 을 기반으로 하고 다양한 좌표에 대해 서로 다른 용어를 기반으로 많은 다른 천체 좌표 시스템 이 있습니다. 수학에 사용된 구형 좌표 시스템은 통상적으로 도(degrees) 가 아닌 라디안(radian) 을 사용되고 수평 좌표 시스템(horizontal coordinate system) 과 같이 북쪽 (0°)에서 동쪽 (+90°)까지 시계 방향이 아닌 x -축에서 y -축까지 반시계 방향으로 방위 각도를 측정합니다.[2] 앙각 (elevation angle )에 의해 대체됩니다; 내림각 (depression angle )은 앙각의 음수입니다.
구형 좌표 시스템은 이-차원 극 좌표 시스템을 일반화합니다. 그것은 역시 고-차원 공간으로 확장될 수 있고, 그런-다음 초구형 좌표 시스템(hyperspherical coordinate system) 으로 참조됩니다.
Definition 구형 좌표 시스템을 정의하기 위해, 두 개의 직교 방향, 천정 (zenith )과 방위 참조 (azimuth reference ), 및 공간에서 원점 (origin )을 선택해야 합니다. 이들 선택 사항은 원점을 포함하고 천정에 수직인 참조 평면을 결정합니다. 점 P 의 구형 좌표는 그런-다음 다음과 같이 정의됩니다:
반지 름(radius ) 또는 방사형 거리 (radial distance )는 원점 O 에서 P 로의 유클리드 거리(Euclidean distance) 입니다.방위 (azimuth, 또는 방위 각도 (azimuthal angle ))는 방위 참조 방향에서 참조 평면 위의 선분 OP 의 직교 투영까지 측정된 부호화된 각도입니다.경사 (inclination 또는 극 각도 (polar angle ))는 천정 방향과 선분 OP 사이의 각도입니다.방위각의 부호는 천정을 중심으로 회전하는 양의 (positive ) 감각이 무엇인지 선택함으로써 결정됩니다. 이 선택은 임의적이고, 좌표 시스템의 정의의 일부입니다.
앙각 (elevation angle)은 참조 평면과 선분 OP 사이의 부호화된 각도이며, 여기서 양의 각도는 천정을 향합니다. 동등하게, 그것은 90도 (π / 2
만약 경사가 영도 또는 180 도 (π 라디안)이면, 방위각은 임의적입니다. 만약 반지름이 영이면, 방위각과 경사는 모두 임의적입니다.
선형 대수(linear algebra) 에서, 원점 O 에서 점 P 까지의 벡터는 종종 P 의 위치 벡터 (position vector )
Conventions 세 개의 좌표를 표현하는 것과, 그것들의 쓰이는 순서에 대한 몇 가지 다른 관례가 있습니다. 방사형 거리, 경사 (또는 고도), 및 방위를 각각 나타내기 위해
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
ISO 표준 80000-2:2019 와 이전 ISO 31-11 (1992)에서 지정됩니다.
어쨌든, 일부 저자 (수학자 포함)는 방사형 거리에 대해 ρ , 경사 (또는 고도)에 대해 φ , 방위각에 대해 θ , 및 z- 축으로부터의 반지름에 대해 r 을 사용하며, 이는 "보통의 극 좌표 표기법의 논리적 확장을 제공합니다".[3] 왼쪽-손(left-handed) 좌표 시스템을 생성합니다. 표준 관례
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
극 좌표(polar coordinates) 와 삼-차원 원통 좌표(cylindrical coordinates) 에 대한 보통의 표기법과 충돌하며, 여기서 θ 는 종종 방위각에 대해 사용됩니다.[3]
각도는 전형적으로 도 (°) 또는 라디안 (rad) 단위로 측정되며, 여기서 360° = 2π rad입니다. 도는 지리학, 천문학, 및 공학에서 가장 공통적이고, 반면에 라디안은 수학과 이론적 물리학에서 공통적으로 사용됩니다. 방사형 거리에 대해 단위는 보통 상황에 따라 결정됩니다.
그 시스템이 물리적인 삼-공간에 대해 사용될 때, 그 평면의 천정 면에서 보았을 때 참조 평면 위에 참조 방향에서 반-시계 방향으로 측정한 방위각은 양의 부호를 사용하는 것이 관례적입니다. 이 관례는, 특히, "천정" 방향이 북쪽이고 양의 방위각 (경도) 각도가 일부 본초 자오선(prime meridian) 에서 동쪽으로 측정되는 지리적 좌표에 사용됩니다.
Major conventions
coordinates
corresponding local geographical directions (Z , X , Y )
right/left-handed
(r , θ inc , φ az,right ) (U , S , E ) right
(r , φ az,right , θ el ) (U , E , N ) right
(r , θ el , φ az,right ) (U , N , E ) left
Note: easting (E ), northing (N ), upwardness (U ). Local azimuth angle would be measured, e.g., counterclockwise from S to E in the case of (U , S , E ) .Unique coordinates 임의의 구형 좌표 세-쌍
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
(
−
r
,
θ
+
180
∘
,
−
φ
)
{\displaystyle (-r,\theta {+}180^{\circ },-\varphi )}
r , θ , 및 φ 에 대해
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
(
r
,
θ
,
−
φ
)
{\displaystyle (r,\theta ,-\varphi )}
(
r
,
θ
+
180
∘
,
φ
)
{\displaystyle (r,\theta {+}180^{\circ },\varphi )}
만약 각 점에 대해 고유한 구형 좌표의 집합을 정의해야 하면, 그것들의 범위를 제한해야 합니다. 공통적인 선택은 다음과 같습니다:
r ≥ 0,0° ≤ θ < 360° (2π rad). 0° ≤ φ ≤ 180° (π rad), 어쨌든, 방위각 θ 는 종종 [0, 360°) 대신, 구간(interval) (−180°, +180°] , 또는 라디안에서 (−π , +π ] 으로 제한됩니다. 이것은 지리적 경도에 대한 표준 관례입니다.
극 각도 φ 에 대해, 경사에 대해 범위 [0°, 180°] 는 고도에 대해 범위 [−90°, +90°] 와 동등합니다. 지리학에서, 위도는 고도입니다.
이들 제한에도 불구하고, 만약 φ 가 0° 또는 180° (고도가 90° 또는 -90°)이면, 방위 각도는 임의적입니다; 그리고 만약 r 이 영이면, 방위 각도와 경사/고도 모두 임의적입니다. 좌표를 고유하게 만들기 위해, 이들 경우에서 임의적인 좌표가 영이라는 관례를 사용할 수 있습니다.
Plotting 구형 좌표 (r , θ , φ ) 에서 점을 그리기 위해, 여기서 θ 가 경사이며, 원점에서 천정 방향으로 r 단위만큼 이동하고, 원점을 기준으로 방위각 참조 방향을 향해 θ 만큼 회전하고, 적절한 방향으로 천정에 대해 φ 만큼 회전합니다.
Applications 이-차원 데카르트 좌표 시스템(Cartesian coordinate system) 이 평면에서 유용하듯이, 이-차원 구형 좌표 시스템은 구의 표면에서 유용합니다. 이 시스템에서, 구는 단위 구(unit sphere) 로 취하므로, 반지름은 일이고, 일반적으로 무시될 수 있습니다. 이 단순화는 회전 행렬(rotational matrices) 과 같은 대상을 다룰 때도 매우 유용할 수 있습니다.
구형 좌표는 구 내부의 부피 적분(volume integrals) , 집중된 질량 또는 전하를 둘러싼 잠재적 에너지 필드, 또는 행성 대기에서 전역적 기상 모의실험과 같이 점에 대해 어느 정도 대칭을 가지는 시스템을 분석하는 데 유용합니다. 데카르트 방정식 x 2 + y 2 + z 2 = c 2 r = c
많은 물리적 문제에서 발생하는 두 가지 중요한 부분 미분 방정식(partial differential equations) , 라플라스의 방정식(Laplace's equation) 과 헬름홀츠 방정식(Helmholtz equation) 은 구형 좌표에서 변수의 분리(separation of variables) 를 허용합니다. rm러한 방정식에 대한 해의 각도 부분은 구형 조화(spherical harmonics) 의 형식을 취합니다.
또 다른 응용 분야는 인체-공학적 설계이며, 여기서 r 은 가만히 있는 사람의 팔 길이이고 각도는 팔이 뻗을 때의 방향을 나타냅니다.
The output pattern of an industrial loudspeaker shown using spherical polar plots taken at six frequencies 확성기(loudspeaker) 출력 패턴의 삼-차원 모델링은 그것들의 성능을 예측하기 위해 사용될 수 있습니다. 주파수에 따라 패턴이 크게 변하기 때문에 다양한 주파수에서 취한 많은 극 그림이 필요합니다. 극 그림은 많은 확성기가 더 낮은 주파수에서 전방향성 경향이 있음을 보여줍니다.
구형 좌표 시스템은 플레이어의 위치를 기준으로 카메라를 회전시키기 위해 3D 게임 개발에서도 공통적으로 사용됩니다.[4]
In geography 첫 번째 근사치로 지리적 좌표 시스템(geographic coordinate system) 은 경사 대신 −90° ≤ φ ≤ 90° 범위에서 적도 평면 북쪽 도 단위에서 앙각 (위도 ψ , q , φ ′, φ c , φ g 지구 중심 위도 (geocentric latitude )지역적 수직(local vertical) 으로 측정되고 공통적으로 φ 로 지정되는 측지 위도 (geodetic latitude )colatitude
공통적으로 λ 로 표시되는 방위 각도 (경도 IERS Reference Meridian )에서 동쪽 또는 서쪽으로 측정되므로, 해당 영역은 −180° ≤ λ ≤ 180° 입니다. 지구 또는 기타 고체 천체의 위치에 대해, 참조 평면은 보통 회전의 축(axis of rotation) 에 수직인 평면으로 취합니다.
방사형 거리 대신 지리학자는 공통적으로 평균 해수면(mean sea level) 일 수 있는 일부 참조 표면 (수직 데이텀 고도 (altitude )r 은 약 6,360 ± 11 km (3,952 ± 7 miles)인 지구의 반지름을 추가함으로써 고도에서 계산될 수 있습니다.
어쨌든, 현대의 지리적 좌표 시스템은 매우 복잡하고, 이들 간단한 공식에 의해 암시되는 위치는 몇 킬로미터나 틀릴 수 있습니다. 위도, 경도, 및 고도의 정확한 표준 의미는 현재 세계 측지 시스템(World Geodetic System , WGS)에 의해 정의되고, 극점에서 지구의 평탄화 (약 21km 또는 13마일)과 기타 많은 세부 사항을 고려합니다.
행성 좌표 시스템(Planetary coordinate systems) 은 지리적 좌표 시스템과 유사한 공식을 사용합니다.
In astronomy 다양한 토대 평면(fundamental planes) 에서 앙각을 측정하기 위해 일련의 천문 좌표 시스템(astronomical coordinate systems) 이 사용됩니다. 이들 참조 평면은 관찰자의 수평선, 천구의 적도 (지구 자전으로 정의됨), 황도의 평면 (태양 주위를 도는 지구 궤도로 정의됨), 지구 종단의 평면 (태양에 대한 순간 방향에 수직), 및 은하 적도 (은하수의 회전으로 정의됨)입니다.
Coordinate system conversions 구형 좌표 시스템은 수많은 삼-차원 좌표 시스템 중 하나일 뿐이므로, 구형 좌표 시스템과 다른 좌표 시스템 사이의 좌표 변환을 위한 방정식이 존재합니다.
Cartesian coordinates ISO 규약에서 점의 구형 좌표 (즉, 물리학에 대해: 반지름 r , 경사 θ , 방위각 φ )는 데카르트 좌표(Cartesian coordinates) (x , y , z ) 에서 다음 공식에 의해 얻을 수 있습니다:
r
=
x
2
+
y
2
+
z
2
θ
=
arccos
z
x
2
+
y
2
+
z
2
=
arccos
z
r
=
{
arctan
x
2
+
y
2
z
if
z
>
0
π
+
arctan
x
2
+
y
2
z
if
z
<
0
+
π
2
if
z
=
0
and
x
y
≠
0
undefined
if
x
=
y
=
z
=
0
φ
=
sgn
(
y
)
arccos
x
x
2
+
y
2
=
{
arctan
(
y
x
)
if
x
>
0
,
arctan
(
y
x
)
+
π
if
x
<
0
and
y
≥
0
,
arctan
(
y
x
)
−
π
if
x
<
0
and
y
<
0
,
+
π
2
if
x
=
0
and
y
>
0
,
−
π
2
if
x
=
0
and
y
<
0
,
undefined
if
x
=
0
and
y
=
0.
{\displaystyle {\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arccos {\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}=\arccos {\frac {z}{r}}={\begin{cases}\arctan {\frac {\sqrt {x^{2}+y^{2}}}{z}}&{\text{if }}z>0\\\pi +\arctan {\frac {\sqrt {x^{2}+y^{2}}}{z}}&{\text{if }}z<0\\+{\frac {\pi }{2}}&{\text{if }}z=0{\text{ and }}xy\neq 0\\{\text{undefined}}&{\text{if }}x=y=z=0\\\end{cases}}\\\varphi &=\operatorname {sgn} (y)\arccos {\frac {x}{\sqrt {x^{2}+y^{2}}}}={\begin{cases}\arctan({\frac {y}{x}})&{\text{if }}x>0,\\\arctan({\frac {y}{x}})+\pi &{\text{if }}x<0{\text{ and }}y\geq 0,\\\arctan({\frac {y}{x}})-\pi &{\text{if }}x<0{\text{ and }}y<0,\\+{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y>0,\\-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y<0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}\end{aligned}}}
φ = arctan y / x 역 탄젠트(inverse tangent) 는 (x , y ) 의 올바른 사분면을 고려하여 적절하게 정의되어야 합니다. atan2 에 대한 기사를 참조하십시오.
대안적으로, 변환은 두 개의 순차적인 데카르트에서 극으로의 변환 으로 고려될 수 있습니다: 첫 번째는 데카르트 xy 평면에서 (x , y ) 에서 (R , φ ) 로, 여기서 R 은 xy -평면 위로의 r 의 투영이고, 두 번째는 데카르트 zR -평면에서 (z , R ) 에서 (r , θ ) 로의 변환입니다. φ 와 θ 에 대한 올바른 사분면은 평면 데카르트에서 극으로의 변환의 정확성에 의해 암시됩니다.
이들 공식은 두 시스템이 같은 원점을 가지고 있고, 구형 참조 평면이 데카르트 xy 평면이고, θ 가 z 방향에서 경사이고, 방위 각도는 (y 축이 φ = +90°x 축에서 측정된다고 가정합니다. 만약 θ 가 천정으로부터의 경사가 아니라 참조 평면으로부터의 고도를 측정하면, 위의 arccos는 arcsin이 되고, 아래의 cos θ 와 sin θ 는 바뀝니다.
반대로, 데카르트 좌표는 구형 좌표 (반지름 r , 경사 θ , 방위각 φ )에서 검색될 수 있으며, 여기서 r ∈ [0, ∞) θ ∈ [0, π ] φ ∈ [0, 2π )
x
=
r
sin
θ
cos
φ
,
y
=
r
sin
θ
sin
φ
,
z
=
r
cos
θ
.
{\displaystyle {\begin{aligned}x&=r\sin \theta \,\cos \varphi ,\\y&=r\sin \theta \,\sin \varphi ,\\z&=r\cos \theta .\end{aligned}}}
Cylindrical coordinates 원통 좌표 (축 반지름 ρ , 방위각 φ , 고도 z )는 다음 공식에 의해 구형 좌표 (중심 반지름 r , 경사 θ , 방위각 φ )로 변환될 수 있습니다:
r
=
ρ
2
+
z
2
,
θ
=
arctan
ρ
z
=
arccos
z
ρ
2
+
z
2
,
φ
=
φ
.
{\displaystyle {\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}},\\\theta &=\arctan {\frac {\rho }{z}}=\arccos {\frac {z}{\sqrt {\rho ^{2}+z^{2}}}},\\\varphi &=\varphi .\end{aligned}}}
반대로, 구형 좌표는 다음 공식에 의해 원통 좌표로 변환될 수 있습니다:
ρ
=
r
sin
θ
,
φ
=
φ
,
z
=
r
cos
θ
.
{\displaystyle {\begin{aligned}\rho &=r\sin \theta ,\\\varphi &=\varphi ,\\z&=r\cos \theta .\end{aligned}}}
이들 공식은 두 시스템이 같은 원점과 같은 참조 평면을 가지고, 같은 축에서 같은 방향으로 방위각 φ 를 측정하고, 구형 각도 θ 가 원통형 z 축에서 경사라고 가정합니다.
Generalization 역시 구형 좌표의 수정된 버전을 사용함으로써 데카르트 좌표에서 타원면체를 다루는 것이 가능합니다.
P를 수준 집합에 의해 지정된 타원면체라고 놓습니다:
a
x
2
+
b
y
2
+
c
z
2
=
d
.
{\displaystyle ax^{2}+by^{2}+cz^{2}=d.}
ISO 규약에서 P에 있는 점의 수정된 구형 좌표 (즉, 물리학에 대해: 반지름 r , 기울기 θ , 방위각 φ )는 데카르트 좌표 (x , y , z ) 에서 다음 공식으로 얻을 수 있습니다:
x
=
1
a
r
sin
θ
cos
φ
,
y
=
1
b
r
sin
θ
sin
φ
,
z
=
1
c
r
cos
θ
,
r
2
=
a
x
2
+
b
y
2
+
c
z
2
.
{\displaystyle {\begin{aligned}x&={\frac {1}{\sqrt {a}}}r\sin \theta \,\cos \varphi ,\\y&={\frac {1}{\sqrt {b}}}r\sin \theta \,\sin \varphi ,\\z&={\frac {1}{\sqrt {c}}}r\cos \theta ,\\r^{2}&=ax^{2}+by^{2}+cz^{2}.\end{aligned}}}
무한소 부피 원소는 다음에 의해 지정됩니다:
d
V
=
|
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
φ
)
|
d
r
d
θ
d
φ
=
1
a
b
c
r
2
sin
θ
d
r
d
θ
d
φ
=
1
a
b
c
r
2
d
r
d
Ω
.
{\displaystyle \mathrm {d} V=\left|{\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}\right|\,dr\,d\theta \,d\varphi ={\frac {1}{\sqrt {abc}}}r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi ={\frac {1}{\sqrt {abc}}}r^{2}\,\mathrm {d} r\,\mathrm {d} \Omega .}
제곱근 인수는 열에서 상수를 추출할 수 있는 행렬식(determinant) 의 속성에서 가져옵니다:
|
k
a
b
c
k
d
e
f
k
g
h
i
|
=
k
|
a
b
c
d
e
f
g
h
i
|
.
{\displaystyle {\begin{vmatrix}ka&b&c\\kd&e&f\\kg&h&i\end{vmatrix}}=k{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}.}
Integration and differentiation in spherical coordinates Unit vectors in spherical coordinates 다음 방정식 (Iyanaga 1977)은 논의된 물리학 관례 에서 처럼 공위도(colatitude) θ 가 z (극) 축으로부터의 경사라고 가정합니다 (x , y , 및 z 가 서로 직교이므로 모호함).
(r , θ , φ ) 에서 (r + dr , θ + dθ , φ + dφ ) 까지의 무한소 변위에 대한 선 원소(line element) 는 다음과 같습니다:
d
r
=
d
r
r
^
+
r
d
θ
θ
^
+
r
sin
θ
d
φ
φ
^
,
{\displaystyle \mathrm {d} \mathbf {r} =\mathrm {d} r\,{\hat {\mathbf {r} }}+r\,\mathrm {d} \theta \,{\hat {\boldsymbol {\theta }}}+r\sin {\theta }\,\mathrm {d} \varphi \,\mathbf {\hat {\boldsymbol {\varphi }}} ,}
r
^
=
sin
θ
cos
φ
x
^
+
sin
θ
sin
φ
y
^
+
cos
θ
z
^
,
θ
^
=
cos
θ
cos
φ
x
^
+
cos
θ
sin
φ
y
^
−
sin
θ
z
^
,
φ
^
=
−
sin
φ
x
^
+
cos
φ
y
^
{\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \cos \varphi \,{\hat {\mathbf {x} }}+\sin \theta \sin \varphi \,{\hat {\mathbf {y} }}+\cos \theta \,{\hat {\mathbf {z} }},\\{\hat {\boldsymbol {\theta }}}&=\cos \theta \cos \varphi \,{\hat {\mathbf {x} }}+\cos \theta \sin \varphi \,{\hat {\mathbf {y} }}-\sin \theta \,{\hat {\mathbf {z} }},\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi \,{\hat {\mathbf {x} }}+\cos \varphi \,{\hat {\mathbf {y} }}\end{aligned}}}
r , θ , 및 φ 의 방향에서 지역적 직교 단위 벡터(unit vectors) 이고,
x
^
{\displaystyle {\hat {\mathbf {x} }}}
y
^
{\displaystyle {\hat {\mathbf {y} }}}
z
^
{\displaystyle {\hat {\mathbf {z} }}}
회전 행렬(rotation matrix) 입니다:
R
=
(
sin
θ
cos
φ
sin
θ
sin
φ
cos
θ
cos
θ
cos
φ
cos
θ
sin
φ
−
sin
θ
−
sin
φ
cos
φ
0
)
.
{\displaystyle R={\begin{pmatrix}\sin \theta \cos \varphi &\sin \theta \sin \varphi &\cos \theta \\\cos \theta \cos \varphi &\cos \theta \sin \varphi &-\sin \theta \\-\sin \varphi &\cos \varphi &0\end{pmatrix}}.}
이것은 구형에서 데카르트로의 변환을 제공하고, 그 반대는 그것의 역에 의해 제공됩니다. 주목: 그 행렬은 직교 행렬입니다. 즉, 그것의 역은 단순히 그것의 전치(transpose) 입니다.
따라서 데카르트 단위 벡터는 다음에 의해 구형 단위 벡터와 관련됩니다:
[
x
^
y
^
z
^
]
=
[
sin
θ
cos
φ
cos
θ
cos
φ
−
sin
φ
sin
θ
sin
φ
cos
θ
sin
φ
cos
φ
cos
θ
−
sin
θ
0
]
[
r
^
θ
^
φ
^
]
{\displaystyle {\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}={\begin{bmatrix}\sin \theta \cos \varphi &\cos \theta \cos \varphi &-\sin \varphi \\\sin \theta \sin \varphi &\cos \theta \sin \varphi &\cos \varphi \\\cos \theta &-\sin \theta &0\end{bmatrix}}{\begin{bmatrix}{\boldsymbol {\hat {r}}}\\{\boldsymbol {\hat {\theta }}}\\{\boldsymbol {\hat {\varphi }}}\end{bmatrix}}}
미분 선 원소를 증명하기 위한 공식의 일반 형식은 다음과 같습니다:[5]
d
r
=
∑
i
∂
r
∂
x
i
d
x
i
=
∑
i
|
∂
r
∂
x
i
|
∂
r
∂
x
i
|
∂
r
∂
x
i
|
d
x
i
=
∑
i
|
∂
r
∂
x
i
|
d
x
i
x
^
i
,
{\displaystyle \mathrm {d} \mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial x_{i}}}\,\mathrm {d} x_{i}=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|{\frac {\frac {\partial \mathbf {r} }{\partial x_{i}}}{\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|}}\,\mathrm {d} x_{i}=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|\,\mathrm {d} x_{i}\,{\hat {\boldsymbol {x}}}_{i},}
r
{\displaystyle \mathbf {r} }
이를 현재 사례에 적용하기 위해, 각 좌표에 따라
r
{\displaystyle \mathbf {r} }
r
=
[
r
sin
θ
cos
φ
r
sin
θ
sin
φ
r
cos
θ
]
.
{\displaystyle \mathbf {r} ={\begin{bmatrix}r\sin \theta \,\cos \varphi \\r\sin \theta \,\sin \varphi \\r\cos \theta \end{bmatrix}}.}
따라서,
∂
r
∂
r
=
[
sin
θ
cos
φ
sin
θ
sin
φ
cos
θ
]
=
r
^
,
∂
r
∂
θ
=
[
r
cos
θ
cos
φ
r
cos
θ
sin
φ
−
r
sin
θ
]
=
r
θ
^
,
∂
r
∂
φ
=
[
−
r
sin
θ
sin
φ
r
sin
θ
cos
φ
0
]
=
r
sin
θ
φ
^
.
{\displaystyle {\frac {\partial \mathbf {r} }{\partial r}}={\begin{bmatrix}\sin \theta \,\cos \varphi \\\sin \theta \,\sin \varphi \\\cos \theta \end{bmatrix}}=\mathbf {\hat {r}} ,\quad {\frac {\partial \mathbf {r} }{\partial \theta }}={\begin{bmatrix}r\cos \theta \,\cos \varphi \\r\cos \theta \,\sin \varphi \\-r\sin \theta \end{bmatrix}}=r\,{\hat {\boldsymbol {\theta }}},\quad {\frac {\partial \mathbf {r} }{\partial \varphi }}={\begin{bmatrix}-r\sin \theta \,\sin \varphi \\r\sin \theta \,\cos \varphi \\0\end{bmatrix}}=r\sin \theta \,\mathbf {\hat {\boldsymbol {\varphi }}} .}
원하는 계수는 다음과 같이 이들 벡터의 크기입니다:[5]
|
∂
r
∂
r
|
=
1
,
|
∂
r
∂
θ
|
=
r
,
|
∂
r
∂
φ
|
=
r
sin
θ
.
{\displaystyle \left|{\frac {\partial \mathbf {r} }{\partial r}}\right|=1,\quad \left|{\frac {\partial \mathbf {r} }{\partial \theta }}\right|=r,\quad \left|{\frac {\partial \mathbf {r} }{\partial \varphi }}\right|=r\sin \theta .}
(일정한) 반지름 r 에서 구형 표면 위의 θ 에서 θ + dθ φ 에서 φ + dφ 표면 원소(surface element) 는 다음과 같습니다:
d
S
r
=
‖
∂
r
∂
θ
×
∂
r
∂
φ
‖
d
θ
d
φ
=
|
r
θ
^
×
r
sin
θ
φ
^
|
=
r
2
sin
θ
d
θ
d
φ
.
{\displaystyle \mathrm {d} S_{r}=\left\|{\frac {\partial {\mathbf {r} }}{\partial \theta }}\times {\frac {\partial {\mathbf {r} }}{\partial \varphi }}\right\|\mathrm {d} \theta \,\mathrm {d} \varphi =\left|r{\hat {\boldsymbol {\theta }}}\times r\sin \theta {\boldsymbol {\hat {\varphi }}}\right|=r^{2}\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi ~.}
따라서 미분 고체 각도(solid angle) 는 다음과 같습니다:
d
Ω
=
d
S
r
r
2
=
sin
θ
d
θ
d
φ
.
{\displaystyle \mathrm {d} \Omega ={\frac {\mathrm {d} S_{r}}{r^{2}}}=\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi .}
극 각도 θ 상수의 표면 (꼭짓점을 원점으로 하는 원뿔)에서 표면 원소는 다음과 같습니다:
d
S
θ
=
r
sin
θ
d
φ
d
r
.
{\displaystyle \mathrm {d} S_{\theta }=r\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} r.}
방위각 φ 상수의 표면 (수직 절반-평면)에서 표면 요소는 다음과 같습니다:
d
S
φ
=
r
d
r
d
θ
.
{\displaystyle \mathrm {d} S_{\varphi }=r\,\mathrm {d} r\,\mathrm {d} \theta .}
r 에서 r + dr θ 에서 θ + dθ φ 에서 φ + dφ 부피 원소(volume element) 는 다음 부분 도함수(partial derivatives) 의 야코비 행렬(Jacobian matrix) 의 행렬식(determinant) 에 의해 지정됩니다:
J
=
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
φ
)
=
(
sin
θ
cos
φ
r
cos
θ
cos
φ
−
r
sin
θ
sin
φ
sin
θ
sin
φ
r
cos
θ
sin
φ
r
sin
θ
cos
φ
cos
θ
−
r
sin
θ
0
)
,
{\displaystyle J={\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}={\begin{pmatrix}\sin \theta \cos \varphi &r\cos \theta \cos \varphi &-r\sin \theta \sin \varphi \\\sin \theta \sin \varphi &r\cos \theta \sin \varphi &r\sin \theta \cos \varphi \\\cos \theta &-r\sin \theta &0\end{pmatrix}},}
d
V
=
|
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
φ
)
|
d
r
d
θ
d
φ
=
r
2
sin
θ
d
r
d
θ
d
φ
=
r
2
d
r
d
Ω
.
{\displaystyle \mathrm {d} V=\left|{\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}\right|\,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi =r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi =r^{2}\,\mathrm {d} r\,\mathrm {d} \Omega ~.}
따라서, 예를 들어, 함수 f (r , θ , φ )삼중 적분(triple integral) 에 의해 R 3
∫
0
2
π
∫
0
π
∫
0
∞
f
(
r
,
θ
,
φ
)
r
2
sin
θ
d
r
d
θ
d
φ
.
{\displaystyle \int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }\int \limits _{0}^{\infty }f(r,\theta ,\varphi )r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi ~.}
이 시스템에서 델(del) 연산자는 그래디언트(gradient) , 다이버전스(divergence) , 컬(curl) , 및 (스칼라) 라플라스(Laplacian) 에 대한 다음 표현식으로 이어집니다:
∇
f
=
∂
f
∂
r
r
^
+
1
r
∂
f
∂
θ
θ
^
+
1
r
sin
θ
∂
f
∂
φ
φ
^
,
∇
⋅
A
=
1
r
2
∂
∂
r
(
r
2
A
r
)
+
1
r
sin
θ
∂
∂
θ
(
sin
θ
A
θ
)
+
1
r
sin
θ
∂
A
φ
∂
φ
,
∇
×
A
=
1
r
sin
θ
(
∂
∂
θ
(
A
φ
sin
θ
)
−
∂
A
θ
∂
φ
)
r
^
+
1
r
(
1
sin
θ
∂
A
r
∂
φ
−
∂
∂
r
(
r
A
φ
)
)
θ
^
+
1
r
(
∂
∂
r
(
r
A
θ
)
−
∂
A
r
∂
θ
)
φ
^
,
∇
2
f
=
1
r
2
∂
∂
r
(
r
2
∂
f
∂
r
)
+
1
r
2
sin
θ
∂
∂
θ
(
sin
θ
∂
f
∂
θ
)
+
1
r
2
sin
2
θ
∂
2
f
∂
φ
2
=
(
∂
2
∂
r
2
+
2
r
∂
∂
r
)
f
+
1
r
2
sin
θ
∂
∂
θ
(
sin
θ
∂
∂
θ
)
f
+
1
r
2
sin
2
θ
∂
2
∂
φ
2
f
.
{\displaystyle {\begin{aligned}\nabla f={}&{\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla \cdot \mathbf {A} ={}&{\frac {1}{r^{2}}}{\partial \over \partial r}\left(r^{2}A_{r}\right)+{\frac {1}{r\sin \theta }}{\partial \over \partial \theta }\left(\sin \theta A_{\theta }\right)+{\frac {1}{r\sin \theta }}{\partial A_{\varphi } \over \partial \varphi },\\[8pt]\nabla \times \mathbf {A} ={}&{\frac {1}{r\sin \theta }}\left({\partial \over \partial \theta }\left(A_{\varphi }\sin \theta \right)-{\partial A_{\theta } \over \partial \varphi }\right){\hat {\mathbf {r} }}\\[8pt]&{}+{\frac {1}{r}}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}\left(rA_{\varphi }\right)\right){\hat {\boldsymbol {\theta }}}\\[8pt]&{}+{\frac {1}{r}}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla ^{2}f={}&{1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}\\[8pt]={}&\left({\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}\right)f+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)f+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}f~.\end{aligned}}}
게다가, 데카르트 좌표에서 역 야코비는 다음과 같습니다:
J
−
1
=
(
x
r
y
r
z
r
x
z
r
2
x
2
+
y
2
y
z
r
2
x
2
+
y
2
−
(
x
2
+
y
2
)
r
2
x
2
+
y
2
−
y
x
2
+
y
2
x
x
2
+
y
2
0
)
.
{\displaystyle J^{-1}={\begin{pmatrix}{\dfrac {x}{r}}&{\dfrac {y}{r}}&{\dfrac {z}{r}}\\\\{\dfrac {xz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\dfrac {yz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\dfrac {-(x^{2}+y^{2})}{r^{2}{\sqrt {x^{2}+y^{2}}}}}\\\\{\dfrac {-y}{x^{2}+y^{2}}}&{\dfrac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}.}
메트릭 텐서(metric tensor) 는
g
=
J
T
J
{\displaystyle g=J^{T}J}
Distance in spherical coordinates 구형 좌표에서, φ 가 방위각 좌표를 갖는 두 점이 주어지면,
r
=
(
r
,
θ
,
φ
)
,
r
′
=
(
r
′
,
θ
′
,
φ
′
)
{\displaystyle {\begin{aligned}{\mathbf {r} }&=(r,\theta ,\varphi ),\\{\mathbf {r} '}&=(r',\theta ',\varphi ')\end{aligned}}}
두 점 사이의 거리는 다음과 같이 나타낼 수 있습니다:
D
=
r
2
+
r
′
2
−
2
r
r
′
(
sin
θ
sin
θ
′
cos
(
φ
−
φ
′
)
+
cos
θ
cos
θ
′
)
{\displaystyle {\begin{aligned}{\mathbf {D} }&={\sqrt {r^{2}+r'^{2}-2rr'(\sin {\theta }\sin {\theta '}\cos {(\varphi -\varphi ')}+\cos {\theta }\cos {\theta '})}}\end{aligned}}}
Kinematics 구형 좌표에서, 점 또는 입자의 위치 (비록 세-쌍
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
[6]
r
=
r
r
^
.
{\displaystyle \mathbf {r} =r\mathbf {\hat {r}} .}
그런-다음 그것의 속도는 다음과 같습니다:[6]
v
=
d
r
d
t
=
r
˙
r
^
+
r
θ
˙
θ
^
+
r
φ
˙
sin
θ
φ
^
{\displaystyle \mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\dot {r}}\mathbf {\hat {r}} +r\,{\dot {\theta }}\,{\hat {\boldsymbol {\theta }}}+r\,{\dot {\varphi }}\sin \theta \,\mathbf {\hat {\boldsymbol {\varphi }}} }
그리고 그것의 가속도는 다음과 같습니다:[6]
a
=
d
v
d
t
=
(
r
¨
−
r
θ
˙
2
−
r
φ
˙
2
sin
2
θ
)
r
^
+
(
r
θ
¨
+
2
r
˙
θ
˙
−
r
φ
˙
2
sin
θ
cos
θ
)
θ
^
+
(
r
φ
¨
sin
θ
+
2
r
˙
φ
˙
sin
θ
+
2
r
θ
˙
φ
˙
cos
θ
)
φ
^
{\displaystyle {\begin{aligned}\mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={}&\left({\ddot {r}}-r\,{\dot {\theta }}^{2}-r\,{\dot {\varphi }}^{2}\sin ^{2}\theta \right)\mathbf {\hat {r}} \\&{}+\left(r\,{\ddot {\theta }}+2{\dot {r}}\,{\dot {\theta }}-r\,{\dot {\varphi }}^{2}\sin \theta \cos \theta \right){\hat {\boldsymbol {\theta }}}\\&{}+\left(r{\ddot {\varphi }}\,\sin \theta +2{\dot {r}}\,{\dot {\varphi }}\,\sin \theta +2r\,{\dot {\theta }}\,{\dot {\varphi }}\,\cos \theta \right){\hat {\boldsymbol {\varphi }}}\end{aligned}}}
각 운동량(angular momentum) 은 다음과 같습니다:
L
=
r
×
p
=
r
×
m
v
=
m
r
2
(
−
φ
˙
sin
θ
θ
^
+
θ
˙
φ
^
)
{\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {r} \times m\mathbf {v} =mr^{2}(-{\dot {\varphi }}\sin \theta \,\mathbf {\hat {\boldsymbol {\theta }}} +{\dot {\theta }}\,{\hat {\boldsymbol {\varphi }}})}
여기서
m
{\displaystyle m}
φ 또는 그밖에 θ = π / 2 극 좌표에서 벡터 미적분 으로 줄어듭니다.
대응하는 각 운동량 연산자(angular momentum operator) 는 위의 위상-공간 재공식화를 따릅니다:
L
=
−
i
ℏ
r
×
∇
=
i
ℏ
(
θ
^
sin
(
θ
)
∂
∂
ϕ
−
ϕ
^
∂
∂
θ
)
.
{\displaystyle \mathbf {L} =-i\hbar ~\mathbf {r} \times \nabla =i\hbar \left({\frac {\hat {\boldsymbol {\theta }}}{\sin(\theta )}}{\frac {\partial }{\partial \phi }}-{\hat {\boldsymbol {\phi }}}{\frac {\partial }{\partial \theta }}\right).}
토크는 다음과 같이 주어집니다:[6]
τ
=
d
L
d
t
=
r
×
F
=
−
m
(
2
r
r
˙
φ
˙
sin
θ
+
r
2
φ
¨
sin
θ
+
2
r
2
θ
˙
φ
˙
cos
θ
)
θ
^
+
m
(
r
2
θ
¨
+
2
r
r
˙
θ
˙
−
r
2
φ
˙
2
sin
θ
cos
θ
)
φ
^
{\displaystyle \mathbf {\tau } ={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F} =-m\left(2r{\dot {r}}{\dot {\varphi }}\sin \theta +r^{2}{\ddot {\varphi }}\sin {\theta }+2r^{2}{\dot {\theta }}{\dot {\varphi }}\cos {\theta }\right){\hat {\boldsymbol {\theta }}}+m\left(r^{2}{\ddot {\theta }}+2r{\dot {r}}{\dot {\theta }}-r^{2}{\dot {\varphi }}^{2}\sin \theta \cos \theta \right){\hat {\boldsymbol {\varphi }}}}
운동 에너지는 다음과 같이 주어집니다:[6]
E
k
=
1
2
m
[
(
r
˙
2
)
+
(
r
θ
˙
)
2
+
(
r
φ
˙
sin
θ
)
2
]
{\displaystyle E_{k}={\frac {1}{2}}m\left[\left({\dot {r}}^{2}\right)+\left(r{\dot {\theta }}\right)^{2}+\left(r{\dot {\varphi }}\sin \theta \right)^{2}\right]}
See also Notes
^ "ISO 80000-2:2019 Quantities and units — Part 2: Mathematics" . ISO . pp. 20–21. Item no. 2-17.3. Retrieved 2020-08-12 .^ Duffett-Smith, P and Zwart, J, p. 34.
^ a b Eric W. Weisstein (2005-10-26). "Spherical Coordinates" . MathWorld . Retrieved 2010-01-15 .^ "Video Game Math: Polar and Spherical Notation" . Academy of Interactive Entertainment (AIE) . Retrieved 2022-02-16 .^ a b "Line element (dl) in spherical coordinates derivation/diagram" . Stack Exchange ^ a b c d e Reed, Bruce Cameron (2019). Keplerian ellipses : the physics of the gravitational two-body problem ISBN 978-1-64327-470-6 OCLC 1104053368 . {{cite book }}: CS1 maint: location (link ) CS1 maint: location missing publisher (link )
Bibliography Iyanaga, Shōkichi; Kawada, Yukiyosi (1977). Encyclopedic Dictionary of Mathematics ISBN 978-0262090162 Morse PM , Feshbach H (1953). Methods of Theoretical Physics, Part I . New York: McGraw-Hill. p. 658. ISBN 0-07-043316-X LCCN 52011515 .Margenau H , Murphy GM (1956). The Mathematics of Physics and Chemistry 177–178 . LCCN 55010911 .Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers . New York: McGraw-Hill. pp. 174–175. LCCN 59014456 . ASIN B0000CKZX7. Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs . New York: Springer Verlag. pp. 95–96. LCCN 67025285 . Moon P, Spencer DE (1988). "Spherical Coordinates (r, θ, ψ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 24–27 (Table 1.05). ISBN 978-0-387-18430-2 Duffett-Smith P, Zwart J (2011). Practical Astronomy with your Calculator or Spreadsheet, 4th Edition . New York: Cambridge University Press. p. 34. ISBN 978-0521146548 External links





































![{\displaystyle {\begin{aligned}\nabla f={}&{\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla \cdot \mathbf {A} ={}&{\frac {1}{r^{2}}}{\partial \over \partial r}\left(r^{2}A_{r}\right)+{\frac {1}{r\sin \theta }}{\partial \over \partial \theta }\left(\sin \theta A_{\theta }\right)+{\frac {1}{r\sin \theta }}{\partial A_{\varphi } \over \partial \varphi },\\[8pt]\nabla \times \mathbf {A} ={}&{\frac {1}{r\sin \theta }}\left({\partial \over \partial \theta }\left(A_{\varphi }\sin \theta \right)-{\partial A_{\theta } \over \partial \varphi }\right){\hat {\mathbf {r} }}\\[8pt]&{}+{\frac {1}{r}}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}\left(rA_{\varphi }\right)\right){\hat {\boldsymbol {\theta }}}\\[8pt]&{}+{\frac {1}{r}}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla ^{2}f={}&{1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}\\[8pt]={}&\left({\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}\right)f+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)f+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}f~.\end{aligned}}}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/175f5c757bb3e3aadcdd97cfd4c7953fa98379e3)











![{\displaystyle E_{k}={\frac {1}{2}}m\left[\left({\dot {r}}^{2}\right)+\left(r{\dot {\theta }}\right)^{2}+\left(r{\dot {\varphi }}\sin \theta \right)^{2}\right]}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/2277f4650b0c4a7dbd0769f0d8f27182a584dd84)