Convex function

Original article: wikipedia:Convex function

Convex function on an interval.

A function (in black) is convex if and only if the region above its graph (in green) is a convex set.

A graph of the bivariate convex function x² + xy + y².

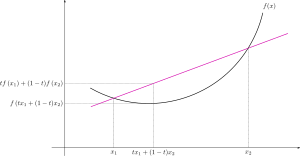
수학(mathematics)에서, n-차원 구간(n-dimensional interval)에서 정의된 실수-값 함수(real-valued function)는, 만약 함수의 그래프(graph of the function) 위의 임의의 두 점 사이의 선분(line segment)이 그래프 위쪽 또는 그래프 위에 놓이면, 볼록(convex) (또는 아래로 볼록(convex downward) 또는 위로 오목(concave upward))으로 불립니다. 동등하게, 함수는, 만약 그의 에피그래프(epigraph) (함수의 그래프 위에 또는 위쪽에 있는 점들의 집합)가 볼록 집합(convex set)이면, 볼록입니다. 단일 변수의 두번-미분가능 함수가 볼록인 것과 그것의 이차 도함수가 그것의 전체 도메인 위에 항상 비-음수인 것은 필요충분(iff) 조건입니다. 단일 변수의 볼록 함수의 잘-알려진 예제는 제곱하는 함수(squaring function) $x^{2}$ 및 지수 함수(exponential function) $e^{x}$를 포함합니다.

볼록 함수는 수학의 많은 분야에서 중요한 역할을 합니다. 그것들은 최적화(optimization) 문제의 연구에서 특히 중요하며, 여기서 그들은 여러 편리한 속성에 의해 구별됩니다. 예를 들어, 열린 집합 위에 엄격하게 볼록 함수는 하나 이상의 최솟값을 가지지 않습니다. 심지어 무한 차원 공간에서, 적절한 추가 가설 아래에서, 볼록 함수는 그러한 속성을 계속 만족시키고 그 결과로써, 그들은 변화의 계산법(calculus of variations)에서 가장 잘-이해된 함수입니다. 확률 이론(probability theory)에서, 확률 변수(random variable)의 기댓값(expected value)에 적용되는 볼록 함수는 확률 변수의 볼록 함수의 기댓값에 의해 항상 위로 경계집니다. 옌센 부등식(Jensen's inequality)으로 알려진, 이 결과는 산술–-기하 평균 부등식(arithmetic–geometric mean inequality) 및 횔더 부등식(Hölder's inequality)과 같은 부등식을 추론하기 위해 사용될 수 있습니다.

Definition

$X$를 실수 벡터 공간(vector space)에서 볼록 집합(convex set)으로 놓고 $f:X\rightarrow \mathbb {R}$를 함수로 놓습니다.

• f는 만약 다음이면 볼록이라고 불립니다:

$\forall x_{1},x_{2}\in X,\forall t\in [0,1]:\qquad f(tx_{1}+(1-t)x_{2})\leq tf(x_{1})+(1-t)f(x_{2})$

• f는 만약 다음이면 엄격하게 볼록이라고 불립니다:

$\forall x_{1}\neq x_{2}\in X,\forall t\in (0,1):\qquad f(tx_{1}+(1-t)x_{2})<tf(x_{1})+(1-t)f(x_{2})$

• 함수 f는, 만약 −f가 (엄격하게) 볼록이면, (엄격하게) 오목(concave)이라고 말합니다.

Properties

Functions of one variable

• $f$를 구간 위에 정의된 하나의 실수(real) 변수의 함수로 가정하고, 다음을 놓습니다:

$R(x_{1},x_{2})={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}$

(R(x₁, x₂)는 상기 그림에서 자주색 직선의 기울기임을 주목하십시오; 함수 R은 (x₁, x₂)에서 대칭(symmetric)입니다). $f$가 볼록인 것과 R(x₁, x₂)가 모든 각 고정된 x₂에 대해 x₁에서 단조적으로 비-감소하는(monotonically non-decreasing) (또는 반대도 마찬가지임) 것은 필요충분 조건입니다. 볼록성의 이 특징은 다음 결과를 입증하기 위해 매우 유용합니다.

• 어떤 열린 구간(open interval) C 위에 정의된 한 실수 변수의 볼록 함수 $f$는 C에서 연속(continuous)입니다. $f$는 왼쪽과 오른쪽 도함수를 허용하고, 이것들은 단조적으로 비-감소하는(monotonically non-decreasing) 것입니다. 결과적으로, $f$는 많아야 셀-수-있게 많은(countably many) 점을 제외하고 나머지에서 미분-가능(differentiable)이며, $f$가 미분-가능하지 않은 집합은 어쨌든 여전히 조밀할 수 있습니다. 만약 C가 닫혀 있으면, $f$는 C의 끝점에서 연속이 되는 것을 실패할 것입습니다 (예제는 예제 섹션에 볼 수 있습니다).
• 한 변수의 미분-가능 함수가 구간 위에 볼록인 것과 그것의 도함수(derivative)가 해당 구간에서 단조적으로 비-감소하는(monotonically non-decreasing) 것은 필요충분 조건입니다. 만약 함수가 미분-가능이고 볼록이면 그것은 역시 연속적으로 미분-가능(continuously differentiable)입니다.
• 한 변수의 미분-가능(differentiable) 함수가 구간 위에 볼록인 것과 그것의 그래프가 구간에서 모든 x와 y에 대해 그것의 모든 접선(tangent) 위에 놓이는 것은 필요충분 조건입니다:

$f(x)\geq f(y)+f'(y)(x-y)$

동등하게, 한 변수의 미분-가능 함수가 볼록인 것과 그것의 에피그래프가 볼록 집합인 것은 필요충분 조건입니다. 특히, 만약 $f'(c)=0$이면, c는 $f(x)$의 전역 최솟값(global minimum)입니다.

• 한 변수의 두번 미분-가능 함수는 구간 위에 볼록인 것과 그것의 이차 도함수(second derivative)가 그곳에서 비-음수인 것은 필요충분 조건입니다; 이것은 볼록성에 대해 실용적인 테스트를 제공합니다. 시각적으로, 두번 미분-가능 볼록 함수는 다른 방법으로 임의의 굽음 (변곡점(inflection point))없이 "위로 휘어집니다". 만약 이차 도함수가 모든 점에서 양수이면, 함수는 엄밀하게 볼록하지만, 전환(converse)은 유지되지 않습니다. 예를 들어, f(x) = x⁴의 이차 도함수는 f ′′(x) = 12x²이며, x = 0에 대해 0이지만, x⁴은 엄격하게 볼록입니다.
• 만약 $f$가 한 실수 변수의 볼록 함수이고, $f(0)\leq 0$이면, $f$는 양의 실수(positive reals) 위에 초-덧셈적(superadditive)입니다.

증명. $f$가 볼록이므로, y = 0을 설정하면 우리는 다음을 가집니다:

$f(tx)=f(tx+(1-t)\cdot 0)\leq tf(x)+(1-t)f(0)\leq tf(x),\quad \forall t\in [0,1]$

이것으로부터, 우리는 다음을 가집니다:

$f(a)+f(b)=f\left((a+b){\frac {a}{a+b}}\right)+f\left((a+b){\frac {b}{a+b}}\right)\leq {\frac {a}{a+b}}f(a+b)+{\frac {b}{a+b}}f(a+b)=f(a+b)$

• 함수는 만약 다음이면 구간 C 위의 중간점 볼록입니다:

$\forall x_{1},x_{2}\in C:\qquad f\left({\frac {x_{1}+x_{2}}{2}}\right)\leq {\frac {f(x_{1})+f(x_{2})}{2}}$

이 조건은 볼록성보다 단지 약간 더 약한 것입니다. 예를 들어, 중간점-볼록인 실수-값 르베그 측정-가능 함수(Lebesgue measurable function)는 볼록입니다: 이것은 시에르핀스키(Sierpiński)의 정리입니다. 특히, 중간-점 볼록인 연속 함수는 볼록일 것입니다.

Functions of several variables

• 여러 변수의 두번 연속적으로 미분-가능 함수는 볼록 집합 위에 볼록인 것과 그것의 이차 부분 도함수(partial derivative)의 헤세 행렬(Hessian matrix)이 볼록 집합의 내부에서 양의 반-한정(positive semidefinite)인 것은 필요충분 조건입니다.
• 볼록 함수의 임의의 지역 최소(local minimum)는 역시 전역 최소(global minimum)입니다. 엄격하게 볼록 함수는 많아야 하나의 전역 최솟값을 가질 것입니다.
• 볼록 함수 $f$에 대해, a ∈ R를 갖는 부분-수준 집합(sublevel set) {x | f(x) < a} 및 {x | f(x) ≤ a}은 볼록 집합입니다. 어쨌든, 그의 부분-수준 집합이 볼록 집합인 함수는 볼록 함수이 아닐 수 있습니다. 그의 부분-수준 집합이 볼록인 함수는 준볼록 함수(quasiconvex function)라고 불립니다.
• 옌센의 부등식(Jensen's inequality)은 모든 각 볼록 함수 $f$에 적용됩니다. 만약 X가 $f$의 도메인에서 값을 취하는 확률 변수이면, $\operatorname {E} (f(X))\geq f(\operatorname {E} (X))$이며, 여기서 E는 수학적 기대(mathematical expectation)를 나타냅니다.
• 한 변수에서 볼록인 두 양의 변수 x와 y의 일-차 동차 함수(homogeneous function) (즉, 각 a,x,y > 0에 대해, f(ax, ay) = a f(x,y))는 다른 변수에서 볼록이어야 합니다.

Operations that preserve convexity

• $-f$가 오목인 것과 $f$가 볼록인 것은 필요충분 조건입니다.
• 비-음의 가중된 합:
  • 만약 $w_{1},\ldots ,w_{n}\geq 0$ 및 $f_{1},\ldots ,f_{n}$가 모두 볼록이면, 따라서 $w_{1}f_{1}+\cdots +w_{n}f_{n}$입니다. 특히, 두 볼록 함수의 합은 볼록입니다.
  • 이 속성은 무한 합, 적분과 (그들이 존재한다는 조건으로 하여) 마찬가지로 기댓값으로 확장됩니다.
• 원소별 최대: $\{f_{i}\}_{i\in I}$를 볼록 집합의 모음으로 놓습니다. 그런-다음 $g(x)=\sup _{i\in I}f_{i}(x)$는 볼록입니다. $g(x)$의 도메인은 표현이 유한인 곳의 모음입니다. 중요한 특별한 경우:
  • 만약 $f_{1},\ldots ,f_{n}$이 볼록 함수이면 따라서 $g(x)=\max\{f_{1}(x),\ldots ,f_{n}(x)\}$입니다.
  • 만약 $f(x,y)$가 x에서 볼록이면 $g(x)=\sup \nolimits _{y\in C}f(x,y)$는 심지어 C가 볼록 집합이 아니더라도 x에서 볼록입니다.
• 합성:
  • 만약 f와 g가 볼록 함수이고 g가 일변수 도메인에 걸쳐 비-감소하는 것이면, $h(x)=g(f(x))$가 볼록입니다. 예제처럼, 만약 $f$가 볼록이면, 따라서 $e^{f(x)}$인데, 왜냐하면 $e^{x}$가 볼록이고 단조적으로 증가하는 것이기 때문입니다.
  • 만약 f가 볼록이고 g가 볼록이고 일변수 도메인에 걸쳐 비-증가하는 것이면, $h(x)=g(f(x))$가 볼록입니다.
  • 볼록성은 아핀 맵 아래에서 불면입니다: 즉, 만약 f가 도메인 $D_{f}\subseteq \mathbf {R} ^{m}$을 갖는 볼록이면, 따라서 $g(x)=f(Ax+b)$이며, 여기서 도메인 $D_{g}\subseteq \mathbf {R} ^{n}$을 갖는 $A\in \mathbf {R} ^{m\times n}{\text{, }}b\in \mathbf {R} ^{m}$입니다.
• 최소화: 만약 $f(x,y)$가 $(x,y)$에서 볼록이면, $g(x)=\inf \nolimits _{y\in C}f(x,y)$가 x에서 볼록이며, C가 볼록 집합이고 $g(x)\neq -\infty$이라는 조건으로 합니다.
• 만약 $f$가 볼록이면, 도메인 $\left\lbrace (x,t)\mid {\tfrac {x}{t}}\in \operatorname {Dom} (f),t>0\right\rbrace$을 갖는 그것의 원근 $g(x,t)=tf\left({\tfrac {x}{t}}\right)$은 볼록입니다.

Strongly convex functions

강한 볼록성의 개념은 엄격한 볼록성의 개념을 확장하고 매개변수화합니다. 강력하게 볼록 함수는 역시 엄격하게 볼록이지만, 그 반대는 아닙니다.

미분-가능 함수 $f$가 만약 다음 부등식이 그것의 도메인에서 모든 점 x, y에 대해 유지되면 매개-변수 m > 0를 갖는 강한 볼록이라고 불립니다:

$(\nabla f(x)-\nabla f(y))^{T}(x-y)\geq m\|x-y\|_{2}^{2}$

또는, 보다 일반적으로,

$\langle \nabla f(x)-\nabla f(y),x-y\rangle \geq m\|x-y\|^{2}$

여기서 $\|\cdot \|$는 임의의 노름(norm)입니다. 차일릿과 같은, 일부 저자는 타원형(elliptic) 함수로 이 부등식을 만족시키는 함수를 참조합니다.

동등한 조건은 다음입니다:

$f(y)\geq f(x)+\nabla f(x)^{T}(y-x)+{\frac {m}{2}}\|y-x\|_{2}^{2}$

미분-가능인 함수에 대해 강하게 볼록이기 위해 미분-가능일 필요는 없습니다. 강하게 볼록 함수에 대해, 매개-변수 m을 갖는 세 번째 정의는 도메인의 모든 x, y와 $t\in [0,1]$에 대해 다음인 것입니다:

$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-{\frac {1}{2}}mt(1-t)\|x-y\|_{2}^{2}$

이 정의는 m → 0으로 엄격한 볼록성에 대해 정의에 접근하고, m = 0일 때 볼록 함수의 정의와 동일함에 주의하십시오. 이것에도 불구하고, 함수는 임의의 m > 0에 대해 엄격하게 볼록이지만 강하게 볼록이 아닌 것이 존재합니다 (아래 예제를 참조하십시오).

만약 함수 $f$가 두번 연속적으로 미분-가능이면, 그것이 매개-변수 m을 갖는 강하게 볼록인 것과 도메인에서 모든 x에 대해 $\nabla ^{2}f(x)\succeq mI$인 것은 필요충분 조건이며, 여기서 I는 항등원이고 $\nabla ^{2}f$는 헤세 행렬(Hessian matrix)이고, 부등호 $\succeq$는 $\nabla ^{2}f(x)-mI$가 양의 반-한정(positive semi-definite)임을 의미합니다. 이것은 $\nabla ^{2}f(x)$의 최소 고윳값(eigenvalue)이 모든 x에 대해 적어도 m인 것을 요구하는 것과 동등합니다. 만약 그 도메인이 단지 실수 직선이면, $\nabla ^{2}f(x)$가 단지 이차 도함수 $f''(x)$이므로, 조건은 $f''(x)\geq m$이 됩니다. 만약 m = 0이면, 이것은 헤세가 양의 반-한정임을 의미하며 (또는 만약 그 도메인이 실수 직선이면, 그것은 $f''(x)\geq 0$임을 의미하며), 이것은 그 함수가 볼록임을 의미하고, 아마도 엄격하게 볼록이지만, 강하게 볼록은 아닙니다.

여전히 함수가 두번 연속적으로 미분-가능이라고 가정하면, 우리는 $\nabla ^{2}f(x)$의 아래쪽 경계가 엄격하게 볼록인 것을 의미하는 것으로 볼 수 있습니다. 테일러의 정리(Taylor's Theorem)를 사용하면, 다음을 만족하는

$f(y)=f(x)+\nabla f(x)^{T}(y-x)+{\frac {1}{2}}(y-x)^{T}\nabla ^{2}f(z)(y-x)$

다음이 존재합니다:

$z\in \{tx+(1-t)y:t\in [0,1]\}$

그런-다음, 고윳값에 대한 정의에 의해,

$(y-x)^{T}\nabla ^{2}f(z)(y-x)\geq m(y-x)^{T}(y-x)$

그리고 따라서 우리가 위의 두 번째 강한 볼록성 방정식을 회복합니다.

함수 $f$가 매개-변수 m을 갖는 강하게 볼록인 것과 다음 함수가 볼록인 것은 필요충분 조건입니다:

$x\mapsto f(x)-{\frac {m}{2}}\|x\|^{2}$.

볼록, 엄격하게 볼록, 및 강하게 볼록 사이에 구별은 언뜻 보기에 미묘할 수 있습니다. 만약 $f$가 두번 연속적으로 미분-가능이고 도메인이 실수 직선이면, 우리는 다음처럼 그것을 특성화할 수 있습니다:

$f$가 볼록인 것과 모든 x에 대해 $f''(x)\geq 0$인 것은 필요충분 조건입니다.

$f$가 만약 모든 x에 대해 $f''(x)>0$이면 엄격하게 볼록입니다 (주목: 이것은 충분이지만, 필요는 아닙니다).

$f$가 강하게 볼록인 것과 모든 x에 대해 $f''(x)\geq m>0$인 것은 필요충분 조건입니다.

예를 들어, $f$를 엄격하게 볼록인 것으로 놓고, $f''(x_{n})={\tfrac {1}{n}}$를 만족하는 점 $(x_{n})$의 수열이 있음을 가정합니다. 심지어 $f''(x_{n})>0$일지라도, 함수는 강하게 볼록인데 왜냐하면 $f''(x)$가 임의적으로 작게 될 것이기 때문입니다.

모든 $x\in X$에 대해 $f''(x)>0$를 만족시키는 컴팩트 도메인 $X$ 위에 두번 연속적으로 미분-가능 함수 $f$는 강하게 볼록입니다. 이 명제의 증명은 극단 값 정리(extreme value theorem)로부터 따르며, 이것은 컴팩트 집합 위에 연속 함수가 최댓값 및 최솟값을 가짐을 말합니다.

강하게 볼록 함수는 일반적으로 볼록 또는 엄격하게 볼록 함수보다 다루기가 더 쉬운데, 왜냐하면 그들은 더 작은 클래스가 있기 때문입니다. 엄격하게 볼록 함수와 마찬가지로, 강하게 볼록 함수는 컴팩트 집합 위에 고유한 최솟값을 가집니다.

Uniformly convex functions

모듈러스 $\phi$와 함께, 균등하게 볼록 함수는 도메인에서 모든 x, y와 t ∈ [0, 1]에 대해, 다음을 만족시키는 함수 $f$입니다:

$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-t(1-t)\phi (\|x-y\|)$

여기서 $\phi$는 비-음수 및 오직 0에서 사라지는 함수입니다. 이것은 강하게 볼록 함수의 개념의 일반화입니다; $\phi (\alpha )={\tfrac {m}{2}}\alpha ^{2}$를 취함으로써 우리는 강한 볼록성의 정의를 회복합니다.

Examples

Functions of one variable

• 함수 $f(x)=x^{2}$는 $f''(x)=2>0$를 가지므로, f는 볼록 함수입니다. 그것은 강한 볼록성 상수 2와 함께, 역시 강하게 볼록입니다 (그리고 따라서 역시 엄격하게 볼록입니다).
• 함수 $f(x)=x^{4}$는 $f''(x)=12x^{2}\geq 0$를 가지므로, f는 볼록 함수입니다. 그것은 심지어 이차 도함수가 모든 점에서 엄격하게 양수가 아닐지라도 엄격하게 볼록입니다. 그것은 강하게 볼록은 아닙니다.
• 절댓값(absolute value) 함수 $f(x)=|x|$는 심지어 점 x = 0에서 도함수를 가지지 않을지라도 (삼각형 부등식(triangle inequality)에 반영된 것처럼) 볼록입니다. 그것은 엄격하게 볼록은 아닙니다.
• 함수 $f(x)=|x|^{p}$는 $p\geq 1$에 대해 볼록입니다.
• 지수 함수(exponential function) $f(x)=e^{x}$는 볼록입니다. 그것은 역시 엄격하게 볼록인데, 왜냐하면 $f''(x)=e^{x}>0$이기 때문입니다. 그러나 강하게 볼록은 아닌데, 왜냐하면 이차 도함수가 임의적으로 영에 가깝지 않기 때문입니다. 보다 일반적으로, 함수 $g(x)=e^{f(x)}$는 만약 f가 볼록 함수이면 로그적으로 볼록(logarithmically convex)입니다. 용어 "초볼록(superconvex)"은 때때로 대신에 사용됩니다.
• $0<x<1$에 대해 $f(0)=f(1)=1,f(x)=0$에 의해 정의된 도메인 [0,1]을 갖는 함수 $f$는 볼록입니다; 그것은 열린 구간 (0, 1) 위에 연속이지만, 0과 1에서 연속이 아닙니다.
• 함수 x³는 이차 도함수 6x를 가집니다; 따라서 그것은 x ≥ 0인 집합 위에 볼록이고 x ≤ 0인 집합 위에 오목(concave)입니다.
• 단조적으로 증가하지만 볼록이 아닌 함수의 예제는 $f(x)={\sqrt {x}}$ 및 $g(x)=\log x$을 포함합니다.
• 볼록이지만 단조적으로 증가하지 않는 함수의 예제는 $h(x)=x^{2}$ 및 $k(x)=-x$를 포함합니다.
• 함수 $f(x)={\tfrac {1}{x}}$는 $f''(x)={\tfrac {2}{x^{3}}}$을 가지며 만약 x > 0이면 영보다 크므로, $f(x)$는 구간 $(0,\infty )$ 위에 볼록입니다. 그것은 구간 $(-\infty ,0)$ 위에 오목입니다.
• $f(0)=\infty$을 갖는 함수 $f(x)={\tfrac {1}{x^{2}}}$는 구간 $(0,\infty )$ 위에 볼록이고 구간 $(-\infty ,0)$ 위에 볼록이지만, 구간 $(-\infty ,\infty )$ 위에 볼록은 아닌데, 왜냐하면 x = 0에서 특이점 때문입니다.

Functions of n variables

• 로그합지수(LogSumExp) 함수는, 역시 소프트맥스(softmax) 함수로 불리며, 볼록 함수입니다.
• 양수-한정 행렬(positive-definite matrices)의 도메인 위에 함수 $-\log \det(X)$는 볼록입니다.
• 모든 각 실수-값 선형 변환(linear transformation)은 볼록이지만, 엄격하게 볼록은 아닌데, 왜냐하면 만약 f가 선형이면, $f(a+b)=f(a)+f(b)$이기 때문입니다. 이 명제는 만약 우리가 "볼록"을 "오목"으로 대체하면 역시 유지됩니다.
• 모든 각 실수-값 아핀 함수(affine function), 즉, 형식 $f(x)=a^{T}x+b$의 각 함수는 동시에 볼록이고 오목입니다.
• 모든 각 노름(norm)은, 삼각형 부등식(triangle inequality)과 양수 동차성(positive homogeneity)에 의해, 볼록 함수입니다.
• 비-음의 행렬(nonnegative matrix)의 스펙트럼 반지름(spectral radius)은 그것의 대각 원소의 볼록 함수입니다.

See also

• Concave function
• Convex optimization
• Convex conjugate
• Geodesic convexity
• Kachurovskii's theorem, which relates convexity to monotonicity of the derivative
• Logarithmically convex function
• Pseudoconvex function
• Quasiconvex function
• Invex function
• Subderivative of a convex function
• Jensen's inequality
• Karamata's inequality
• Hermite–Hadamard inequality
• K-convex function

References

• Bertsekas, Dimitri (2003). Convex Analysis and Optimization. Athena Scientific.
• Borwein, Jonathan, and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.
• Donoghue, William F. (1969). Distributions and Fourier Transforms. Academic Press.
• Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
• Krasnosel'skii M.A., Rutickii Ya.B. (1961). Convex Functions and Orlicz Spaces. Groningen: P.Noordhoff Ltd.
• Lauritzen, Niels (2013). Undergraduate Convexity. World Scientific Publishing.
• Luenberger, David (1984). Linear and Nonlinear Programming. Addison-Wesley.
• Luenberger, David (1969). Optimization by Vector Space Methods. Wiley & Sons.
• Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.
• Thomson, Brian (1994). Symmetric Properties of Real Functions. CRC Press.
• Zălinescu, C. (2002). Convex analysis in general vector spaces. River Edge, NJ: World Scientific Publishing  Co., Inc. pp. xx+367. ISBN 981-238-067-1. MR 1921556.

External links

• "Convex function (of a real variable)", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Convex function (of a complex variable)", Encyclopedia of Mathematics, EMS Press, 2001 [1994]