Necessity and sufficiency

논리(logic)와 수학(mathematics)에서, 필요(necessity) 및 충분(sufficiency)은 두 명제(statements) 사이의 조건부(conditional) 또는 함축적 관계를 설명하기 위해 사용되는 용어입니다. 예를 들어, 조건부 명제: "만약 P이면 Q입니다"에서, Q는 P에 대해 필요인데, 왜냐하면 P의 진리가 Q의 진리를 보장하기 때문입니다 (동등하게, Q없이 P를 가지는 것이 불가능합니다).^[1]^[2] 비슷하게, P가 Q에 대해 충분인데, 왜냐하면 참인 P는 Q가 참임을 항상 의미하기 하지만, 참이 아닌 P는 Q가 참이 아님을 항상 의미하지는 않기 때문입니다.^[3]

일반적으로, 필요 조건은 또 다른 조건에 대해 발생하기 위해 존재해야 하는 조건이지만, 충분 조건은 말했던 조건을 생성하는 조건입니다.^[4] 한 명제가 또 다른 명제의 "필요 및 충분" 조건이라는 주장은 전자 명제가 참인 것과 후자가 참인 것은 필요충분(iff) 조건입니다.^[5] 즉, 두 명제는 동시에 참, 또는 동시에 거짓이어야 합니다.^[6]^[7]^[8]

보통의 영어(ordinary English)에서, "필요"와 "충분"은 명제가 아닌 일의 조건 또는 상태 사이의 관계를 나타냅니다. 예를 들어, 남녀를 준수하는 가정에서, 남자가 되는 것은 형제가 되기 위한 필수 조건이지만, 충분은 아닙니다–반면에 남자 형제가 되는 것은 형제가 되기 위한 필요 및 충분 조건입니다.

Definitions

조건부 명제, "만약 S이면, N입니다"에서, S에 의해 표시된 표현은 전제(antecedent)라고 불리고, N에 의해 표시된 표현은 결론(consequent)이라고 불립니다. 이 조건부 명제는 "N 만약 S",, "S 오직 만약 S", "S는 N을 의미합니다", "N은 S에 의해 의미됩니다", $S \to N$ , $S \Rightarrow N$ 및 "S일 때마다 N과 같은 여러 동등한 방법으로 쓸 수 있습니다. ^[9]

위의 상황에서, N은 S에 대해 필요 조건이라고 말합니다. 공통 언어에서, 이것은 만약 조건부 명제가 참 명제이면, 결론 N이 반드시 참이어야 한다는 말하는 것과 동등합니다–만약 S가 참이면 (바로 아래의 "진리 테이블(truth table)"의 세 번째 열을 참조하십시오). 달리 말해서, 전제 S는 참이 되는 N없이 절대 참이 될 수 없습니다. 예를 들어, 누군가에 대해 소크라테스(S)라고 불리기 위해, 그 누군가를 이름-짓는(N) 것이 필요합니다. 비슷하게, 인간에 대해 살아가기 위해, 그들은 공기를 가지는 것이 필요합니다.^[10]

위의 상황에서, 우리는 S는 N에 대해 충분 조건임을 역시 말할 수 있습니다 (바로 아래의 진리 테이블의 세 번째 열을 다시 참조하십시오). 만약 조건부 명제가 참이면, 그런-다음 만약 S가 참이면, N은 참이어야 합니다; 반면에 만약 조건부 명제가 참이고 N이 참이면, S는 참 또는 거짓일 수 있습니다. 일반적인 용어에서, "S의 진리는 N의 진리를 보장합니다".^[10] 예를 들어, 앞의 예제에서 계속해서, 우리는 누군가가 소크라테스(S)라고 불리는 것을 아는 것은 누군가가 이름(N)을 가짐을 알기 위해 충분합니다.

필요 및 충분 조건은 함축 $S\Rightarrow N$ 및 $N\Rightarrow S$ (그것의 후자는 $S\Leftarrow N$ 으로 역시 쓸 수 있음) 둘 다가 유지되는 것을 요구합니다. 첫 번째 함축은 S가 N에 대해 충분 조건임을 암시하지만, 두 번째 함축은 S가 N에 필요 조건임을 암시합니다. 이것은 "S는 N에 대해 필요 및 충분입니다", "S if and only if N ", 또는 $S\Leftrightarrow N$ 로 표현됩니다.^[5]

Truth table
$S$	$N$	$S\Rightarrow N$	$S\Leftarrow N$	$S\Leftrightarrow N$
T	T	T	T	T
T	F	F	T	F
F	T	T	F	F
F	F	T	T	T

Necessity

Q가 P에 대해 필요라는 역설은 구어체적으로 "P는 만약 Q가 참이 아니면 절대 참이 될 수 없습니다" 또는 "만약 Q가 거짓이면, P는 거짓입니다"와 동등합니다.^[10]^[2] 대우(contraposition)에 의해, 이것은 "P가 참일 때마다, Q도 마찬가지입니다"와 같은 것입니다.

P와 Q 사이의 논리적 관계는 "만약 P이면, Q입니다"로 표현되고 "P ⇒ Q"로 표시됩니다 (P는 Q를 의미(implies)합니다). 그것은 역시 "P 오직 만약 Q", "Q, 만약 P", "P일 때마다 Q", 및 "P일 때 Q" 중 임의의 것으로 표현될 수 있습니다. 우리는 종종, 예를 들어, 수학적 산문에서, 예제 5에 보인 것처럼, 함께 취해져서, 충분 조건을 구성하는 여러 필요 조건 (즉, 개별적으로 필요이고 결합적으로 충분^[10])이 발견합니다.

예제 1

"존은 미혼-남자입니다"가 참인 것에 대해, 그가 다음인 것이 역시 참인 것은 필요입니다:

미혼,
남자,
성인,

왜냐하면 "존이 미혼-남자입니다"를 말하는 것은 그들의 세 추가적인 술어(predicates)를 가짐을 의미합니다:

예제 2: 2보다 큰 자연수에 대해, 홀수가 되는 것은 소수가 되는 것에 필요인데, 왜냐하면 2는 짝수와 소수 둘 다인 유일한 자연수이기 때문입니다.

예제 3: 번개로 인한 천둥, 소리를 생각해 보십시오. 우리는 천둥는 번개에 대해 필요라고 말하는데, 왜냐하면 번개는 천둥없이 발생하지 않기 때문입니다. 번개가 있을 때마다, 천둥가 있습니다. 천둥은 번개를 일으키지 않지만 (번개는 천둥을 유발하기 때문에), 번개는 항상 천둥과 함께 오기 때문에, 우리는 천둥은 번개에 대해 필요라고 말합니다. (즉, 그것의 형식적인 의미에서, 필요는 인과-관계를 의미하지 않습니다.)

예제 4: 적어도 30살이 되는 것은 미국 상원에서 봉사하는 것에 대해 필요입니다. 만약 30살 아래이면, 상원 의원이 될 수 없습니다. 즉, 만약 상원 의원이면, 그것은 적어도 30살이어야 함을 따릅니다.

예제 5: 대수(algebra)에서, 그룹(group)을 형성하기 위한 연산(operation) $\star$ 과 함께 일부 집합(set) S에 대해, $\star$ 가 결합적(associative)인 것이 필요입니다. S가 S에서 모든 각 x에 대해, e $\star$ x 및 x $\star$ e가 x와 둘 다 같은 것을 만족하는 특수 원소 e를 포함하는 것은 역시 필요입니다. S에서 모든 각 x에 대해 x $\star$ x″ 및 x″ $\star$ x 둘 다가 특수 원소 e와 같음을 만족하는 해당하는 원소 x″가 있는 것은 필요입니다. 자체로 이들 세 필요 조건은 어떤 것은 충분은 아니지만, 셋의 논리곱(conjunction)은 충분입니다.

Sufficiency

만약 P가 Q에 대해 충분이면, 참인 P를 아는 것은 Q가 참이라고 결론을 내리기에 충분한 근거입니다; 어쨌든, 거짓인 P를 아는 것은 Q가 거짓이라고 결론을 내릴 최소한의 요구를 충족시키지 못합니다.

논리적 관계는, 이전과 같이, "만약 P이면, Q" 또는 "P ⇒ Q"로 표현됩니다. 이것은 "P 오직 만약 Q", "P는 Q를 의미합니다" 또는 여러 다른 변형으로 역시 표현될 수 있습니다. 여러 충분 조건이, 합쳐질 때, 예제 5에 묘사된 것처럼 단일의 필요 조건 (즉, 개별적으로 충분 및 결합적으로 필요)을 구성하는 경우일 수 있습니다.

예제 1: "존은 왕입니다"는 존이 남자임을 의미합니다. 따라서 존이 왕인 것을 아는 것은 그가 남자인 것을 아는 것에 대한 충분입니다.

예제 2: 4로 나뉠 수 있는 숫자는 짝수인 것에 대해 충분이지만 (필요하지는 아니며), 2로 나뉠 수 있는 것은 충분 및 필요 둘 다입니다.

예제 3: 천둥의 발생은 천둥이 들리는 것을 의미하는 번개의 발생에 대해 충분 조건이고, 그것을 명백하게 인식하면 번개가 있었다는 결론을 정당화합니다.

예제 4: 만약 미국 의회가 법안을 통과하면, 법안의 대통령의 서명은 그것을 법률로 만드는 것에 충분입니다. 대통령이 법안에 서명하지 않은 것에 의해 경우는, 예를 들어 대통령 거부권(veto) 행사를 통해, 법안이 법률이 되지 않았다는 것을 의미하지는 않음에 주목하십니다 (예를 들어, 의회의 재정의(override)를 통해 여전히 법률이 될 수 있습니다).

예제 5: 카드가 에이스가 되기 위해서는 플레잉 카드(playing card)의 중앙에 하나의 큰 스페이드 (♠)가 표시되어야 합니다. 세 다른 충분 조건은 카드 중앙에 단일 다이아몬드 (♦), 하트 (♥), 또는 클럽 (♣)이 표시되어 있다는 것입니다. 카드가 에이스가 되기 위해서는 이들 조건들 중 어느 것도 필요이지 않지만, 이들 조건 중 적어도 하나 (실제로, 정확히)를 충족함없이 에이스가 될 수 없기 때문에 그들의 논리합(disjunction)입니다.

Relationship between necessity and sufficiency

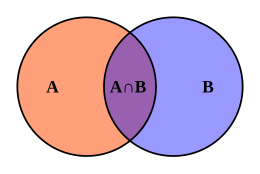
조건은 다른 조건없이 필요 또는 충분 중 하나일 수 있습니다. 예를 들어, 포유 동물(mammal)인 것 (N)은 사람인 것 (S)은 필요이지만 충분은 아니고, 숫자 $x$ 가 유리수인 것 (S)은 $x$ 가 실수(real number)인 것 (N)은 충분이지만 필요는 아닙니다 (왜냐하면 유리수가 아닌 실수가 있기 때문입니다).

조건은 필요 및 충분 둘 다일 수 있습니다. 예를 들어, 현재, "오늘은 7월 4일입니다"는 "오늘은 미국(United States)에서 독립 기념일(Independence Day)입니다"에 대해 필요 및 충분 조건입니다. 비슷하게, 행렬(matrix) M의 역-가능성(invertibility)에 대해 필요 및 충분 조건은 M이 비-영 행렬식(determinant)을 가지는 것입니다.

수학적으로 말하면, 필요성과 충분성은 서로 이중(dual)입니다. 임의의 명제 S 및 N에 대해, "N은 S에 대해 필요입니다"는 주장은 "S가 N에 대해 충분입니다"는 주장과 동등합니다. 이러한 이중성의 또 다른 관점은, 위에서 묘사된 것처럼, 필요 조건의 논리곱 ("그리고"를 사용함)이 충분성을 달성할 수 있지만, 충분 조건의 논리합 ("또는"을 사용함)은 필요성을 달성할 수 있다는 것입니다. 세 번째 관점에 대해, N이 참을 유지시키는 것에 대해 대상, 사건, 또는 명제의 집합 T(N)을 갖는 모든 각 수학적 술어(predicate) N을 식별하십시오; 그런-다음 S에 대해 N의 필요성을 주장하는 것은 T(N)이 T(S)의 초월-집합(superset)이라고 주장하는 것과 동등하지만, N에 대해 S의 충분성을 주장하는 것은 T(S)가 T(N)의 부분-집합(subset)이라고 주장하는 것과 동등합니다.

Simultaneous necessity and sufficiency

P가 Q에 대해 필요 및 충분이라고 말하는 것은 두 가지를 말하는 것입니다:

P가 Q에 대해 필요, $P\Leftarrow Q$ 이고, P가 Q에 대해 충분, $P\Rightarrow Q$ 입니다.
동등하게, P와 Q가 나머지 하나에 대해 필요, $P\Rightarrow Q\land Q\Rightarrow P$ 임을 말하는 것으로 이해될 수 있으며, 이것은 각각이 나머지 하나에 대해 충분입니다 또는 다른 하나를 의미합니다로 역시 말할 수 있습니다.

우리는 $P\Leftrightarrow Q$ 에 의해 표시되는 명제 "P if and only if Q"에 의해 이들 경우의 임의의 것, 및 따라서 모두를 요약할 수 있지만, 경우들은 $P\Leftrightarrow Q$ 가 $P\Rightarrow Q\land Q\Rightarrow P$ 와 동일하다는 것을 말합니다.

예를 들어, 그래프 이론(graph theory)에서 그래프 G는 만약 G의 모든 각 가장자리가 각 색상의 하나의 끝점을 갖는 그러한 방법에서 각 꼭짓점에 검정 또는 흰색을 할당하는 것이 가능하면 이분(bipartite)이라고 불립니다. 그리고 이분되는 임의의 그래프에 대해, 홀수-길이 순환(cycles)을 포함하지 않는 것이 필요 및 충분 조건입니다. 따라서 그래프가 임의의 홀수 순환을 갖는지 여부를 발견하는 것은 그래프가 이분인지 및 반대인지 여부를 말합니다. 철학자는^[11] 따라서 일의 이러한 상태를 다음과 같이 특징-지을 수 있습니다: "비록 이분성의 개념과 홀수 순환의 부재는 내부-내용(intension)에서 다를지라도, 그것들은 동일한 확장(extension)을 가집니다. ^[12]

수학에서, 정리는 형식 "P가 참인 것과 Q가 참인 것은 필요충분 조건입니다"으로 종종 표시됩니다. 그들의 증명은 통상적으로 먼저 충분성, 예를 들어 $P\Rightarrow Q$ 을 입증합니다. 둘째, 그 반대가 입증되며, $Q\Rightarrow P$

둘 다 직접적으로, Q가 참임을 가정하고 Q 순환이 P 이내에 위치됨을 시연합니다. 또는
대우적으로(contrapositively), 즉 P의 원 밖으로 나가면, 우리는 Q 밖으로 떨어짐: P가 아님을 가정하면, Q가 아님이 초래되는 것을 시연합니다.

이것은 Q와 P에 대해 그 원이 위의 벤-다이어그램 위에 일치함을 입증합니다.

이전 섹션에서 설명한 것처럼, 다른 하나에 대해 하나의 필요성은 첫 번째 하나에 대해 다른 하나의 충분성과 동등하며, 예를 들어 $P\Leftarrow Q$ 는 $Q\Rightarrow P$ 와 동등(equivalent)합니다. 만약 P가 Q에 대해 필요 및 충분이면, Q는 P에 대해 필요 및 충분입니다. 우리는 $P\Leftrightarrow Q\equiv Q\Leftrightarrow P$ 를 쓸 수 있고, 명제 "P가 참인 것과 Q가 참인 것은 필요충분(iff)입니다" 및 "Q가 참인 것과 P가 참인 것은 필요충분입니다"라고 말합니다.

References

^ "The Definitive Glossary of Higher Mathematical Jargon — Necessity". Math Vault. 2019-08-01. Retrieved 2019-12-02.{{cite web}}: CS1 maint: url-status (link)
^ ^a ^b "[M06] Necessity and sufficiency". philosophy.hku.hk. Retrieved 2019-12-02.
^ Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. pp. 8–9. ISBN 978-1-4419-7126-5.
^ Confusion-of-Necessary (2019-05-15). "Confusion of Necessary with a Sufficient Condition". www.txstate.edu. Retrieved 2019-12-02.
^ ^a ^b "The Definitive Glossary of Higher Mathematical Jargon — Iff". Math Vault. 2019-08-01. Retrieved 2019-12-02.{{cite web}}: CS1 maint: url-status (link)
^ Betz, Frederick (2011). Managing Science: Methodology and Organization of Research. New York: Springer. p. 247. ISBN 978-1-4419-7487-7.
^ Manktelow, K. I. (1999). Reasoning and Thinking. East Sussex, UK: Psychology Press. ISBN 0-86377-708-2.
^ Asnina, Erika; Osis, Janis; Jansone, Asnate (2013). "Formal Specification of Topological Relations". Databases and Information Systems VII: 175. doi:10.3233/978-1-61499-161-8-175. {{cite journal}}: Unknown parameter |last-author-amp= ignored (|name-list-style= suggested) (help)
^ Devlin, Keith (2004), Sets, Functions and Logic / An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall, pp. 22–23, ISBN 978-1-58488-449-1
^ ^a ^b ^c ^d "The Concept of Necessary Conditions and Sufficient Conditions". www.sfu.ca. Retrieved 2019-12-02.
^ Stanford University primer, 2006.
^ "Meanings, in this sense, are often called intensions, and things designated, extensions. Contexts in which extension is all that matters are, naturally, called extensional, while contexts in which extension is not enough are intensional. Mathematics is typically extensional throughout." Stanford University primer, 2006.

External links

Critical thinking web tutorial: Necessary and Sufficient Conditions
Simon Fraser University: Concepts with examples

[1] "The Definitive Glossary of Higher Mathematical Jargon — Necessity". Math Vault. 2019-08-01. Retrieved 2019-12-02.{{cite web}}: CS1 maint: url-status (link)

[:0-2] "[M06] Necessity and sufficiency". philosophy.hku.hk. Retrieved 2019-12-02.

[3] Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. pp. 8–9. ISBN 978-1-4419-7126-5.

[4] Confusion-of-Necessary (2019-05-15). "Confusion of Necessary with a Sufficient Condition". www.txstate.edu. Retrieved 2019-12-02.

[:1-5] "The Definitive Glossary of Higher Mathematical Jargon — Iff". Math Vault. 2019-08-01. Retrieved 2019-12-02.{{cite web}}: CS1 maint: url-status (link)

[betz-6] Betz, Frederick (2011). Managing Science: Methodology and Organization of Research. New York: Springer. p. 247. ISBN 978-1-4419-7487-7.

[Manktelow-7] Manktelow, K. I. (1999). Reasoning and Thinking. East Sussex, UK: Psychology Press. ISBN 0-86377-708-2.

[asnina-8] Asnina, Erika; Osis, Janis; Jansone, Asnate (2013). "Formal Specification of Topological Relations". Databases and Information Systems VII: 175. doi:10.3233/978-1-61499-161-8-175. {{cite journal}}: Unknown parameter |last-author-amp= ignored (|name-list-style= suggested) (help)

[9] Devlin, Keith (2004), Sets, Functions and Logic / An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall, pp. 22–23, ISBN 978-1-58488-449-1

[:2-10] "The Concept of Necessary Conditions and Sufficient Conditions". www.sfu.ca. Retrieved 2019-12-02.

[stan-11] Stanford University primer, 2006.

[12] "Meanings, in this sense, are often called intensions, and things designated, extensions. Contexts in which extension is all that matters are, naturally, called extensional, while contexts in which extension is not enough are intensional. Mathematics is typically extensional throughout." Stanford University primer, 2006.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Necessity and sufficiency

Definitions

Necessity

Sufficiency

Relationship between necessity and sufficiency

Simultaneous necessity and sufficiency

See also

Argument forms involving necessary and sufficient conditions

Valid forms of argument

Invalid forms of argument (i.e. fallacies)

References

External links