Pyramid (geometry)

Regular-based right pyramids
Regular-based right pyramids
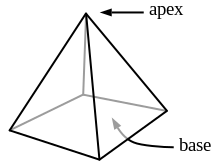	Example: square pyramid
Faces	n triangles; 1 n-sided polygon
Edges	2n
Vertices	n + 1
Schläfli symbol	( ) ∨ {n}
Conway notation	Yn
Symmetry group	Cnv, [1,n], (*nn), order 2n
Rotation group	Cn, [1,n]+, (nn), order n
Dual polyhedron	self-dual
Properties	convex

기하학(geometry)에서, 각뿔(pyramid) (from el πυραμίς (pyramís)^[1]^[2])는 다각형(polygonal) 밑면과 꼭대기(apex)라고 하는 한 점을 연결함으로써 형성된 다면체(polyhedron)입니다. 각 밑면 가장자리와 꼭대기는 측면(lateral face)이라고 하는 삼각형을 형성합니다. 그것은 다각형 밑면을 갖는 원뿔형 고체(conic solid)입니다. n-변 밑면을 갖는 각뿔는 $n + 1$ 개의 꼭짓점(vertices), $n + 1$ 개의 면(faces), 및 $2 n$ 개의 가장자리(edges)를 가지고 있습니다. 모든 각뿔는 자기-이중(self-dual)적입니다.

직각 각뿔(right pyramid)은 그것의 밑변의 도형중심(centroid) 바로 위에 그것의 꼭대기를 가집니다. 비-직각 각뿔은 경사 각뿔(oblique pyramids)이라고 합니다. 정규 각뿔(regular pyramid)은 정규 다각형(regular polygon) 밑변을 가지고 보통 직각 각뿔(right pyramid)임을 암시합니다.^[3]^[4]

지정되지 않았을 때, 각뿔은 보통 물리적 각뿔(pyramid) 구조와 같은 정규 정사각형 각뿔(square pyramid)로 가정됩니다. 삼각형-밑변 각뿔은 더 자주 사면체(tetrahedron)라고 불립니다.

예각과 둔각 삼각형(acute and obtuse triangles)과 같은 경사 각뿔 중에서, 각뿔은 그것의 꼭대기가 밑변의 내부보다 위에 있으면 예각(acute)이라고 하고 꼭대기가 밑변의 외부보다 위에 있으면 둔각(obtuse)이라고 할 수 있습니다. 직각 각뿔(right-angled pyramid)은 밑변의 가장자리 또는 꼭짓점 위에 그것의 꼭대기를 가집니다. 사면체에서, 이들 한정자는 어떤 면이 밑변으로 고려되는지에 따라 변경됩니다.

각뿔은 각기둥형(prismatoids)의 클래스입니다. 각뿔은 밑변 평면의 다른 쪽에 두 번째 오프셋 점을 추가함으로써 쌍-각뿔(bipyramids)을 두 배로 만들 수 있습니다.

Right pyramids with a regular base

정규 밑면을 갖는 직각 각뿔은 이등변 삼각형 측면을 가지며, 대칭은 C_nv 또는 [1,n]이고, 차수 2n을 가집니다. 그것은 정규 다각형(regular polygon), {n}에 (직교적으로 오프셋) 결합된 한 점, ( )을 나타내는 확장된 슐래플리 기호(Schläfli symbol) ( ) ∨ {n}이 주어질 수 있습니다. 결합 연산은 두 결합된 그림의 모든 꼭짓점 쌍 사이에 새 가장자리를 만듭니다.^[5]

모든 등변 삼각형(equilateral triangle) 면을 갖는 삼각형 각뿔(trigonal 또는 triangular pyramid)은 플라톤 고체(Platonic solids) 중 하나, 정규(regular) 사면체(tetrahedron)가 됩니다. 삼각형 각뿔(triangular pyramid)의 하부 대칭 경우는 등변 삼각형 밑변과 3개의 동일한 이등변 삼각형 측면을 가지는 C_3v입니다. 정사각형과 오각형 각뿔은 역시 정규 볼록 다각형으로 구성될 수 있으며, 이 경우에서 그것들은 존슨 고체(Johnson solids)입니다.

만약 정사각형 각뿔 (또는 임의의 볼록 다면체)의 모든 가장자리는 접하는 점의 평균 위치가 구의 중심에 있도록 구(sphere)에 접(tangent)하면, 각뿔은 정식(canonical)이라고 말해지고, 그것은 정규 팔면체(octahedron)의 절반을 형성합니다.

육각형 이상의 밑변을 갖는 각뿔은 이등변 삼각형으로 구성되어야 합니다. 등변 삼각형을 갖는 육각형 각뿔은 완전하게 평평한 도형일 것이고, 칠각형 이상은 삼각형이 전혀 만나지 않을 것입니다.

Regular pyramids
Digonal	Triangular	Square	Pentagonal	Hexagonal	Heptagonal	Octagonal	Enneagonal	Decagonal...
Improper	Regular	Equilateral		Isosceles

Right star pyramids

정규 별 다각형(regular star polygon)의 밑면을 갖는 직각 각뿔은 별 각뿔(star pyramids)이라고 합니다.^[6] 예를 들어, 오각형 각뿔은 오각형(pentagram) 밑변과 5개의 교차하는 삼각형 면을 가집니다.

Right pyramids with an irregular base

직각 각뿔(right pyramid)은 ( )∨P로 이름-지어질 수 있으며, 여기서 ( )는 꼭대기, ∨는 결합 연산자이고, P는 밑변 다각형입니다.

이등변 삼각형 직각 사면체(isosceles triangle right tetrahedron)는 이등변 삼각형 밑면에 대한 점의 결합으로 ( )∨[( )∨{ }]로, 4개의 이등변 삼각형 면을 포함하는 2개의 직교 세그먼트, 대각선 디스피노이드(digonal disphenoid)의 결합 (직교 오프셋)으로 [( )∨( )]∨{ } 또는 { }∨{ }로 쓸 수 있습니다. 그것은 두 개의 서로 다른 밑변-꼭대기 방향에서 C_1v 대칭을 가지고, 완전한 대칭에서 C_2v를 가집니다.

( )∨[{ }×{ }]로 쓰인 직사각형(rectangular) 직각 각뿔(right pyramid) 과 ( )∨[{ }+{ }]로 쓰인 마름모(rhombic) 각뿔(pyramid)은 모두 대칭 C_2v를 가집니다.

Right pyramids
Rectangular pyramid	Rhombic pyramid

Volume

각뿔 (역시 임의의 원뿔)의 부피(volume)는 $V={\tfrac {1}{3}}bh$ , 여기서 b는 밑면의 넓이이고 h는 밑면에서 꼭대기까지의 높이입니다. 이것은, h가 밑면을 포함하는 평면(plane)으로부터 수직(perpendicular) 거리로 측정된다는 조건 아래에서, 임의의 다각형, 정규 또는 비-정규, 및 꼭대기의 임의의 위치에 대해 작동합니다. 기원후 499년에, 인도 수학(Indian mathematics)과 인도 천문학(Indian astronomy)의 고전 시대로부터 수학자이자-천문학자(mathematician-astronomer), 아리아바타(Aryabhata)는 Aryabhatiya (2.6절)에서 이 방법을 사용했습니다.

그 공식은 미적분학을 사용하여 공식적으로 증명될 수 있습니다. 닮음에 의해, 밑면에 평행한 단면의 선형 치수는 꼭대기에서 밑변까지 선형적으로 증가합니다. 스케일링 인수 (비례 인수)는 $1-{\tfrac {y}{h}}$ , 또는 ${\tfrac {h-y}{h}}$ 이며, 여기서 h는 높이이고 y는 밑면에서 교차-단면까지의 수직 거리입니다. 임의의 교차-단면의 넓이(area)는 모양의 스케일링(scaling) 인수의 제곱에 비례하므로, 높이 y에서의 교차-단면의 넓이는 $b{\tfrac {(h-y)^{2}}{h^{2}}}$ 이거나, b와 h 둘 다가 상수이므로, ${\tfrac {b}{h^{2}}}(h-y)^{2}$ 입니다. 그 부피는 적분(integral)에 의해 주어집니다:

{\frac {b}{h^{2}}}\int _{0}^{h}(h-y)^{2}\,dy={\frac {-b}{3h^{2}}}(h-y)^{3}{\bigg |}_{0}^{h}={\tfrac {1}{3}}bh.

같은 방정식, $V={\tfrac {1}{3}}bh$ 은 역시 임의의 밑변을 갖는 원뿔에 대해 유지됩니다. 이것은 위의 것과 유사한 논증으로 증명될 수 있습니다. 원뿔의 부피(volume of a cone)를 참조하십시오.

예를 들어, 밑변이 변 길이 s를 갖는 n-변 정규 다각형(regular polygon)이고 높이가 h인 각뿔의 부피는 다음과 같습니다:

V={\frac {n}{12}}hs^{2}\cot {\frac {\pi }{n}}.

그 공식은 직사각형 밑변을 갖는 각뿔에 대해 미적분없이 정확하게 유도될 수도 있습니다. 단위 정육면체를 생각해 보십시오. 정육면체의 중심에서 8개의 각 꼭짓점까지 직선을 그리십시오. 이것은 정육면체를 밑면 넓이 1과 높이 1/2인 6개의 같은 정육면체 각뿔로 나눕니다. 각 각뿔은 분명히 1/6의 부피를 가집니다. 이것으로부터, 우리는 각뿔 부피 = 높이 × 밑면 넓이 / 3임을 추론합니다.

다음으로, 결과 직사각형 고체 가장자리가 a, b, 및 c이고, 고체 부피 abc를 갖도록 정육면체를 같지 않은 양만큼 세 방향에서 균등하게 확장하십시오. 내부의 6개의 각뿔의 각각은 마찬가지로 확장됩니다. 그리고 각 각뿔은 같은 부피 abc/6를 가집니다. 각뿔의 쌍은 높이 a/2, b/2, 및 c/2를 가지므로, 우리는 각뿔 부피 = 높이 × 밑면 넓이 / 3임을 다시 알 수 있습니다.

변 삼각형이 등변일 때, 부피에 대해 그 공식은 다음과 같습니다:

V={\frac {1}{12}}ns^{3}\cot \left({\frac {\pi }{n}}\right){\sqrt {1-{\frac {1}{4\sin ^{2}{\tfrac {\pi }{n}}}}}}.

이 공식은 n = 2, 3, 4, 및 5에만 적용됩니다; 그것은 역시 그 부피가 영과 같은 것 (즉, 각뿔 높이가 영)에 대해, n = 6 경우을 다룹니다.^{[citation needed]}

Surface area

각뿔의 표면 넓이(surface area)는 $SA=B+{\tfrac {1}{2}}PL$ 이며, 여기서 B는 밑면 넓이, P는 밑면 둘레(perimeter)이고, 경사 높이(slant height) $L={\sqrt {h^{2}+r^{2}}}$ 이며, 여기서 h는 각뿔 고도이고 r은 밑면의 내반지름(inradius)입니다.

Centroid

각뿔의 도형중심(centroid)은 꼭대기(apex)와 밑면의 도형중심을 연결하는 선분 위에 놓입니다. 고체 각뿔에 대해, 도형중심은 밑변에서 꼭대기까지의 거리의 1/4입니다.

n-dimensional pyramids

2-차원 각뿔은 꼭대기(apex)라고 하는 동일선상에 있지 않은 점에 연결된 밑변 가장자리에 의해 형성된 삼각형입니다.

4-차원 각뿔은 다면체 각뿔(polyhedral pyramid)이라고 하며, 4-공간의 3-공간 초평면에 있는 다면체(polyhedron)와 해당 초평면에서 또 다른 점에 의해 구성됩니니다.

더 높은 차원의 각뿔은 역시 유사하게 구성됩니다.

심플렉스(simplices)의 가족은 삼각형(triangle), 사면체(tetrahedron), 5-셀(5-cell), 5-심플렉스(5-simplex), 등으로 증가하는 임의의 차원에서 각뿔을 나타냅니다. n-차원 심플렉스는 최소 n+1개의 꼭짓점(vertices)을 가지며, 가장자리(edges)에 의해 연결된 모든 꼭짓점의 쌍, 면을 정의하는 모든 세 쌍의 꼭짓점, 사면체 셀(cells)을 정의하는 모든 네 쌍의 점, 등을 가집니다.

Polyhedral pyramid

4-차원 기하학(geometry)에서, 다면체 각뿔(polyhedral pyramid)은 밑면 다면체(polyhedron) 셀과 꼭대기(apex) 점에 의해 구성된 4-폴리토프(4-polytope)입니다. 측면 패싯(facets)은 각뿔 셀이며, 각각은 밑변 다면체의 한 면과 꼭대기로 구성됩니다. 다면체 각뿔의 꼭짓점과 가장자리는 평면 그래프(planar graph) (밑변의 그래프)에 꼭짓점 (꼭대기) 하나를 추가함으로써 형성된 그래프, 꼭대기 그래프(apex graphs)의 예제를 형성합니다.

정규 5-셀(5-cell) (또는 4-심플렉스(simplex))은 사면체 각뿔의 예제입니다. 1보다 작은 둘레-반지름을 갖는 균등 다면체는 정규 사면체 면을 갖는 다면체 각뿔을 만들 수 있습니다. v 꼭짓점, e 가장자리, 및 f 면을 갖는 다면체는 v+1 꼭짓점, e+v 가장자리, f+e 면, 및 1+f 셀을 갖는 다면체 각뿔의 밑면이 될 수 있습니다.

축 대칭을 갖는 4D 다면체 각뿔은 정점을 밑면 다면체의 중심에 꼭대기를 배치하는 3D 투영, Schlegel 다이어그램(Schlegel diagram)을 갖는 3D로 시각화될 수 있습니다.

Equilateral uniform polyhedron-based pyramids (Schlegel diagram)
Symmetry	[1,1,4]	[1,2,3]	[1,3,3]	[1,4,3]		[1,5,3]
Name	Square-pyramidal pyramid	Triangular prism pyramid	Tetrahedral pyramid	Cubic pyramid	Octahedral pyramid	Icosahedral pyramid
Segmentochora index^[7]	K4.4	K4.7	K4.1	K4.26.1	K4.3	K4.84
Height	0.707107	0.645497	0.790569	0.500000	0.707107	0.309017
Image (Base)
Base	Square pyramid	Triangular prism	Tetrahedron	Cube	Octahedron	Icosahedron

임의의 볼록 4-폴리토프는 내부 점을 추가하고 각 패싯에서 중심점까지 하나의 각뿔을 생성함으로써 다면체 각뿔(polyhedral pyramids)로 나뉠 수 있습니다. 이것은 부피를 계산하는 데 유용할 수 있습니다.

다면체 각뿔의 4-차원 초부피는 밑변의 길이 곱하기 높이의 1/2인 삼각형의 넓이와 밑면의 넓이 곱하기 높이의 1/3인 각뿔의 부피와 비교하여, 밑변 다면체의 부피 곱하기 그것의 수직 높이의 1/4입니다.

다면체 각뿔의 3-차원 표면 부피는 $SV=B+{\tfrac {1}{3}}AL$ 이며, 여기서 B는 밑면 부피, A는 밑면 표면 넓이이고, L은 경사 높이 (측면 각뿔 셀의 높이) $L={\sqrt {h^{2}+r^{2}}}$ 이며, 여기서 h는 높이이고 r은 내반지름입니다.

References

^ πυραμίς, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus Digital Library
^ The word meant "a kind of cake of roasted wheat-grains preserved in honey"; the Egyptian pyramids were named after its form (R. S. P. Beekes, Etymological Dictionary of Greek, Brill, 2009, p. 1261).
^ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p. 46
^ Civil Engineers' Pocket Book: A Reference-book for Engineers Archived 2018-02-25 at the Wayback Machine
^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms
^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 50, ISBN 978-0-521-09859-5, archived from the original on 2013-12-11.
^ Convex Segmentochora Archived 2014-04-19 at the Wayback Machine Dr. Richard Klitzing, Symmetry: Culture and Science, Vol. 11, Nos. 1–4, 139–181, 2000

External links

Weisstein, Eric W. "Pyramid". MathWorld.

[1] πυραμίς, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus Digital Library

[2] The word meant "a kind of cake of roasted wheat-grains preserved in honey"; the Egyptian pyramids were named after its form (R. S. P. Beekes, Etymological Dictionary of Greek, Brill, 2009, p. 1261).

[3] William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p. 46

[4] Civil Engineers' Pocket Book: A Reference-book for Engineers Archived 2018-02-25 at the Wayback Machine

[5] N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms

[6] Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 50, ISBN 978-0-521-09859-5, archived from the original on 2013-12-11.

[Segmentochora-7] Convex Segmentochora Archived 2014-04-19 at the Wayback Machine Dr. Richard Klitzing, Symmetry: Culture and Science, Vol. 11, Nos. 1–4, 139–181, 2000

[1]

[2]

[3]

[4]

[5]

[6]

[7]