Quadratic formula

Original article: w:Quadratic formula

A quadratic function with roots x = 1 and x = 4.

기초 대수학(elementary algebra)에서, 이차 공식(quadratic formula)은 이차 방정식(quadratic equation)에 대한 해를 제공하는 공식입니다. 이차 공식을 사용하는 것 대신에 이차 방정식을 푸는 다른 방법, 예를 들어, 인수화(factoring) (직접 인수화, 묶기, AC 방법), 제곱식을 완성(completing the square), 또는 그래프(graphing), 등이 있습니다.

미지수를 나타내는 $x$, $a\neq 0$을 갖는, 상수(constant)를 나타내는 $a$, $b$ 및 $c$와 함께, 다음 형식의 일반적인 이차 방정식이 주어지면:

$ax^{2}+bx+c=0$.

이차 공식은 다음입니다:

$$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \$$

여기서 양-음 기호 "±"(plus-minus symbol "±")는 이차 방정식이 두 개의 해를 가짐을 가리킵니다. 분리해서 쓰면, 그들은 다음이 됩니다:

$x_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\quad {\text{and}}\quad x_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}$

이들 두 해의 각각은 이차 방정식의 근 또는 영(root or zeor)으로 불립니다. 기하학적으로, 이들 근은, $y=ax^{2}+bx+c$로 명시적으로 주어진, 임의의 포물선(parabola)이 $x$-축과 교차하는 것에서 $x$ 값을 나타냅니다.

마찬가지로 임의의 포물선의 영을 산출하는 공식이 될 것이며, 이차 공식은 포물선의 대칭축, 및 이차 방정식이 포함하는 실수(real) 영의 개수를 식별하기 위해 역시 사용될 수 있습니다.

Equivalent formulations

이차 공식은 다음으로 역시 쓸 수 있습니다:

$x={\frac {-b}{2a}}\pm {\sqrt {\frac {b^{2}-4ac}{4a^{2}}}}\ \ ,$

이것은 다음으로 단순화될 수 있습니다:

$x=-{\frac {b}{2a}}\pm {\sqrt {\left({\frac {b}{2a}}\right)^{2}-{\frac {c}{a}}}}\ \ .$

공식의 이 버전은 복소수 근이 포함될 때 편리합니다. 이 경우에서 제곱근 외부의 표현은 실수 부분이 될 것이고 제곱근 표현은 허수 부분이 될 것입니다. 제곱근 내부의 표현은 하나의 판별식입니다.

Muller's method

뮬러의 방법(Muller's method)에서 사용되고 비에타의 공식(Vieta's formulas)에서 구할 수 있는, 덜 알려진 이차 공식은 다음 방정식을 통해 같은 근을 제공합니다:

$x={\frac {-2c}{b\mp {\sqrt {b^{2}-4ac}}}}={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac\ }}}}\ \ .$

Formulations based on alternative parametrizations

이차 방정식의 표준 매개변수화는 다음입니다:

$ax^{2}+bx+c=0\ \ .$

일부 출처, 특히 오래된 출처는 다음과 같은 이차 방정식의 대안적인 매개변수화를 사용합니다:

$ax^{2}-2b_{1}x+c=0$, where $b_{1}=-b/2$,

또는

$ax^{2}+2b_{2}x+c=0$, where $b_{2}=b/2$.

이들 대안적인 매개변수화는 해에 대해 약간 다른 형식의 결과를 낳지만, 표준 매개변수화에 대한 기타의 점에서 동등합니다.

Derivations of the formula

이차 공식을 유도하기 위한 많은 다른 방법들이 문헌에서 유용합니다. 표준적인 하나는 제곱식을 완성(completing the square) 기법의 간단한 응용입니다. 대안적인 방법은 때때로 제곱식을 완성하는 것보다 더 간단하고, 수학의 다른 영역에 대한 흥미로운 통찰력을 제공할 수 있습니다.

By using the 'completing the square' technique

Standard method

이차 방정식을 $a$로 나눕니다. 이것은 $a$가 비-영이기 때문에 허용됩니다:

$x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0\ \ .$

방정식의 양쪽 변으로부터 c/a를 빼면, 다음을 산출합니다:

$x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}\ \ .$

이차 방정식은 이제 제곱식을 완성(completing the square)의 방법이 적용될 수 있는 형식입니다. 실제로, 왼쪽 변이 완전 제곱식이 되는 것을 만족하는 상수를 방정식의 양쪽 변에 더함으로써, 방정식은 다음이 됩니다:

$x^{2}+{\frac {b}{a}}x+\left({\frac {b}{2a}}\right)^{2}=-{\frac {c}{a}}+\left({\frac {b}{2a}}\right)^{2}\ \ ,$

이것은 다음을 산출합니다:

$\left(x+{\frac {b}{2a}}\right)^{2}=-{\frac {c}{a}}+{\frac {b^{2}}{4a^{2}}}\ \ .$

그에 따라서 공통 분모를 갖도록 오른쪽 변에서 항을 다시-정렬한 후에, 우리는 다음을 얻습니다:

$\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}\ \ .$

제곱식은 따라서 완성되었습니다. 양쪽 변에 제곱근(square root)을 취함으로써 다음 방정식을 산출합니다:

$x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}\ \ .$

이 경우에서, $x$를 분리하면 이차 공식을 제공할 것입니다:

$x={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}\ \ .$

대부분 $a$의 조작과 관련하여, 사소한 차이를 가진 이 유도의 많은 대안들이 있습니다.

Method 2

지난 수십 년 동안 출판된 대수학 교과서의 대부분은 이전에 제시된 순서를 사용하여 제곱식을 완성(completing the square)하는 것을 가르칩니다:

1. 일계수(monic) 다항식을 만들기 위해 양쪽 변을 $a$로 나누십시오.
2. 재배열하십시오.
3. 제곱식을 완성하기 위해 양쪽 변에 $\textstyle \left({\frac {b}{2a}}\right)^{2}$를 더하십시오.
4. 공통 분모를 가지기 위해 오른쪽 변에서 항을 재배열하십시오.
5. 양쪽 변의 제곱 근을 취하십시오.
6. $x$를 분리하십시오.

1975년에 래리 호흔(Larry Hoehn)에 의해 지적된 것처럼, 제곱식을 완성하는 것은 더 짧고 간단한 순서로 수행될 수 있습니다:

1. 양쪽 변에 $4a$을 곱하십시오.
2. 재배열하십시오.
3. 제곱식을 완성하기 위해 양쪽 변에 $b^{2}$를 더하십시오.
4. 양쪽 변의 제곱근을 취하십시오.
5. $x$를 분리하십시오.

이 경우에서, 이차 공식은 다음으로 역시 유도될 수 있습니다:

${\begin{aligned}ax^{2}+bx+c&=0\\4a^{2}x^{2}+4abx+4ac&=0\\4a^{2}x^{2}+4abx&=-4ac\\4a^{2}x^{2}+4abx+b^{2}&=b^{2}-4ac\\(2ax+b)^{2}&=b^{2}-4ac\\2ax+b&=\pm {\sqrt {b^{2}-4ac}}\\2ax&=-b\pm {\sqrt {b^{2}-4ac}}\\x&={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .\end{aligned}}$

이것은 실제로 이차 공식의 고전적인 유도를 나타내고 적어도 1025년으로 거슬러 올라가서 힌두교인에게 알려졌었습니다. 표준 사용법의 유도와 비교하면, 이 대안적인 유도는 더 간단하고 짧은데, 왜냐하면 마지막 단계까지 분수와 제곱된 분수를 피하고 그러므로 그것은 오른쪽 변에서 공통 분모를 얻기 위한 단계 3 다음에 재배열을 요구하지 않기 때문입니다.

Method 3

방법 1과 비슷하게, 왼쪽 변을 다항식 일계수(monic)로 만들기 위해 양쪽 변을 $a$로 나누십시오 (즉, $x^{2}$의 계수가 1이 됩니다).

$x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0\ \ .$

보다 간결하고 다루기-쉬운 형식으로 방정식을 쓰십시오:

$x^{2}+Bx+C=0$

여기서 $\textstyle B={\frac {b}{a}}$ 및 $\textstyle C={\frac {c}{a}}$입니다.

첫 번째 항에 $\textstyle {\frac {B^{2}}{4}}$을 더해서 제곱식을 완성하고 그것을 세 번째 항으로부터 빼십시오:

$\left(x+{\frac {B}{2}}\right)^{2}+\left(C-{\frac {B^{2}}{4}}\right)=0$

왼쪽 변을 두 제곱의 차이(difference of two squares)로 재정렬하십시오:

$\left(x+{\frac {B}{2}}\right)^{2}-\left({\sqrt {{\frac {B^{2}}{4}}-C}}\right)^{2}=0$

그리고 그것을 인수화하십시오:

$\left(x+{\frac {B}{2}}+{\sqrt {{\frac {B^{2}}{4}}-C}}\right)\left(x+{\frac {B}{2}}-{\sqrt {{\frac {B^{2}}{4}}-C}}\right)=0$

이것은 다음 둘 중 하나임을 의미합니다:

$x+{\frac {B}{2}}+{\sqrt {{\frac {B^{2}}{4}}-C}}=0$

또는

$x+{\frac {B}{2}}-{\sqrt {{\frac {B^{2}}{4}}-C}}=0$

이들 두 방정식의 각각은 선형이고 $x$에 대해 풀릴 수 있으며, 다음을 획득합니다:

$x=-{\frac {B}{2}}-{\sqrt {{\frac {B^{2}}{4}}-C}}$ 또는 $x=-{\frac {B}{2}}+{\sqrt {{\frac {B^{2}}{4}}-C}}$

$B$ 및 $C$를, 각각, $\textstyle {\frac {b}{a}}$ 및 $\textstyle {\frac {c}{a}}$으로 다시-표현함으로써, 이차 공식은 그런-다음 획득될 수 있습니다.

By substitution

또 다른 기법은 치환(substitution)에 의한 해입니다. 이 기법에서, 우리는 $x=y+m$을 다음을 얻기 위해 이차에 치환합니다:

$a(y+m)^{2}+b(y+m)+c=0\ \ .$

결과를 전개하고 그런 다음 $y$의 거듭제곱을 정리하면 다음을 생성합니다:

$ay^{2}+y(2am+b)+\left(am^{2}+bm+c\right)=0\ \ .$

우리는 아직 $y$와 $m$에 대한 두 번째 조건을 부과하지 않았으므로, 우리는 이제 중간 항을 없애도록 $m$을 선택합니다. 즉, $2am+b=0$ 또는 $\textstyle m={\frac {-b}{2a}}$입니다. 방정식의 양쪽 변으로부터 상수 항을 빼고 그런-다음 $a$로 나누면 다음을 제공합니다:

$y^{2}={\frac {-\left(am^{2}+bm+c\right)}{a}}\ \ .$

$m$에 대해 치환하면 다음을 제공합니다:

$y^{2}={\frac {-\left({\frac {b^{2}}{4a}}+{\frac {-b^{2}}{2a}}+c\right)}{a}}={\frac {b^{2}-4ac}{4a^{2}}}\ \ .$

그러므로,

$y=\pm {\frac {\sqrt {b^{2}-4ac}}{2a}}$

공식 $\textstyle x=y+m=y-{\frac {b}{2a}}$을 사용하여 $x$의 관점에서 $y$를 다시-표현하면, 보통의 이차 공식은 그런-다음 획득될 수 있습니다:

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .$

By using algebraic identities

다음 방법은 역사적으로 많은 수학자에 의해 사용되었습니다:

표준 이차 방정식의 근을 r₁ 및 r₂로 놓습니다. 유도는 다음 항등식을 기억해냄으로써 시작합니다:

$(r_{1}-r_{2})^{2}=(r_{1}+r_{2})^{2}-4r_{1}r_{2}\ \ .$

양쪽 변에 대해 제곱근을 취하면, 우리는 다음을 얻습니다:

$r_{1}-r_{2}=\pm {\sqrt {(r_{1}+r_{2})^{2}-4r_{1}r_{2}}}\ \ .$

계수 a ≠ 0이므로, 우리는 같은 근들을 가지는 이차 다항식을 얻기 위해 a로 표준 방정식을 나눌 수 있습니다. 즉,

$x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=(x-r_{1})(x-r_{2})=x^{2}-(r_{1}+r_{2})x+r_{1}r_{2}\ \ .$

이것으로부터 우리는 표준 이차 방정식의 근의 합이 −b/a로 제공되고, 그들 근의 곱은 c/a로 제공됨을 알 수 있습니다. 그러므로 항등식은 다음으로 다시 쓸 수 있습니다:

$r_{1}-r_{2}=\pm {\sqrt {\left(-{\frac {b}{a}}\right)^{2}-4{\frac {c}{a}}}}=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}-{\frac {4ac}{a^{2}}}}}=\pm {\frac {\sqrt {b^{2}-4ac}}{a}}\ \ .$

이제,

$r_{1}={\frac {(r_{1}+r_{2})+(r_{1}-r_{2})}{2}}={\frac {-{\frac {b}{a}}\pm {\frac {\sqrt {b^{2}-4ac}}{a}}}{2}}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .$

r₂ = −r₁ − b/a이므로, 만약 우리가 다음을 취하면

$r_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}$

그런-다음 우리는 다음을 획득합니다:

$r_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\ \ ;$

그리고 만약 우리가 대신에 다음을 취하면

$r_{1}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}$

그런-다음 우리는 다음임을 계산합니다:

$r_{2}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\ \ .$

표준 속기법 ±를 사용하여 이들 결과를 연결하면, 우리는 이차 방정식의 해가 다음으로 제공되는 것을 가집니다:

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .$

By Lagrange resolvents

Further information: Lagrange resolvents

이차 공식을 유도하는 대안적인 방법은, 갈루아 이론(Galois theory)의 초기 부분인, 라그랑주 분해(Lagrange resolvents)의 방법을 통한 것입니다. 이 방법은 삼차 다항식(cubic polynomial)과 사차 다항식(quartic polynomial)의 근을 제공하기 위해 일반화될 수 있고, 갈루아 이론으로 이어지며, 이것은 우리에게 그들의 근의 대칭 그룹(symmetry group), 갈루아 그룹(Galois group)의 관점에서 임의의 차수의 대수 방정식의 해를 이해하는 것을 허용합니다.

이 접근법은 원래 방정식을 재정렬하는 것보다 근에 집중합니다. 일계수 이차 방정식이 주어지면:

$x^{2}+px+q\ \ ,$

그것이 다음으로 인수화되는 것을 가정합니다:

$x^{2}+px+q=(x-\alpha )(x-\beta )\ \ ,$

전개하면 다음을 산출합니다:

$x^{2}+px+q=x^{2}-(\alpha +\beta )x+\alpha \beta \ \ ,$

여기서 p = −(α + β) 및 q = αβ입니다.

곱셈의 순서는 문제가 되지 않으므로, 우리는 α와 β의 위치를 바꿀 수 있고 p와 q의 값은 변하지 않을 것입니다: 우리는 p와 q는 α와 β에서 대칭 다항식(symmetric polynomials)임을 말할 수 있습니다. 사실, 그들은 기초 대칭 다항식(elementary symmetric polynomials)입니다 – α와 β에서 임의의 대칭 다항식은 α + β 및 αβ의 관점에서 표현될 수 있습니다. 다항식을 분석하고 해결하기 위한 갈루아 이론 접근법은 다음입니다: 근에서 대칭 함수인, 다항식의 계수가 주어지면, "대칭을 깨고" 근을 복구할 수 있습니까? 따라서 차수 n의 다항식을 푸는 것은 n 항을 재정렬하는 ("순열하는") 방법과 관련되는데, 이것은 n 문자에 대한 대칭 그룹(symmetric group)이라고 불리고, S_n으로 나타냅니다. 이차 다항식에 대해, 두 항을 재정렬하기 위한 유일한 방법은 그들의 위치를 바꾸는 것 (그들을 "전치(transpose)"하는 것)이고, 따라서 이차 방정식을 푸는 것은 간단합니다.

근 α 및 β를 찾기 위해, 그들의 합과 차이를 생각해 보십시오:

${\begin{aligned}r_{1}&=\alpha +\beta \\r_{2}&=\alpha -\beta \ \ .\end{aligned}}$

이들은 다항식의 라그랑주 분해(Lagrange resolvents)로 불립니다; 이것들 중 하나는 근의 순서에 의존하며, 이것이 핵심임을 주목하십시오. 우리는 위의 방정식을 반대로 정리함으로써 분해로부터 근을 복구할 수 있습니다:

${\begin{aligned}\alpha &=\textstyle {\frac {1}{2}}\left(r_{1}+r_{2}\right)\\\beta &=\textstyle {\frac {1}{2}}\left(r_{1}-r_{2}\right)\ \ .\end{aligned}}$

따라서, 분해에 대해 푸는 것은 원래 근을 제공합니다.

이제 r₁ = α + β은 α와 β에서 대칭 함수이므로, 그것은 p와 q의 관점에서 표현될 수 있고, 위에서 주목한 것처럼 사실 r₁ = −p입니다. 그러나 r₂ = α − β는 대칭이 아닌데, 왜냐하면 α와 β의 위치를 바꾸면 −r₂ = β − α를 생성하기 때문입니다 (공식적으로, 이것은 근의 대칭 그룹의 그룹 동작(group action)이라고 이름 짓습니다). r₂는 대칭이 아니므로, 그것은 계수 p와 q의 관점에서 절대 표현될 수 없는데, 왜냐하면 이들은 근에서 대칭이고 따라서 그들을 포함하는 임의의 다항 표현도 마찬가지입니다. 근의 순서를 바꾸는 것은 r₂를 –1의 인수만큼 오직 변하고, 따라서 제곱 r₂² = (α − β)²는 근에서 대칭이고, 따라서 p와 q의 관점에서 표현 가능합니다. 다음 방정식을 사용하여

$(\alpha -\beta )^{2}=(\alpha +\beta )^{2}-4\alpha \beta \ \$

다음을 산출합니다:

$r_{2}^{2}=p^{2}-4q\ \$

따라서

$r_{2}=\pm {\sqrt {p^{2}-4q}}\ \$

만약 우리가 양의 근을 취하면, 대칭이 깨지고, 다음을 획득합니다:

${\begin{aligned}r_{1}&=-p\\r_{2}&={\sqrt {p^{2}-4q}}\end{aligned}}$

따라서

${\begin{aligned}\alpha &={\tfrac {1}{2}}\left(-p+{\sqrt {p^{2}-4q}}\right)\\\beta &={\tfrac {1}{2}}\left(-p-{\sqrt {p^{2}-4q}}\right)\ \ .\end{aligned}}$

따라서 근은 다음입니다:

$\textstyle {\frac {1}{2}}\left(-p\pm {\sqrt {p^{2}-4q}}\right)$

이것은 이차 공식입니다. p = b/a, q = c/a으로 치환하는 것은 이차가 일계수가 아닐 때에 대해 보통 형식을 산출합니다. 분해는 꼭짓점이 되는 r₁/2 = −p/2 = −b/2a으로 인식될 수 있고, r₂² = p² − 4q는 (일계수 다항식의) 판별식입니다.

비슷하지만 보다 복잡한 방법은 삼차 방정식(cubic equation)에 대해 작동하며, 여기서 우리는 세 분해 및 r₂와 r₃와 관련된 ("분해되는 다항식") 이차 방정식을 가지며, 우리는 그 이차 방정식을 풀 수 있고, 비슷하게 사차 방정식(quartic equation)에 대해, 그의 분해되는 다항식은 삼차이고, 그것은 차례로 풀릴 수 있습니다. 오차 방정식(quintic equation)에 대해 같은 방법은 차수 24의 다항식을 생성하며, 이것은 문제를 단순화하지 않고, 사실, 일반적으로 오차 방정식에 대한 해는 오직 근을 사용하여 절대 표현될 수 없습니다.

By extrema

함수의 극점에서 x의 값을 아는 것은 이차 방정식을 풀기 위한 x에 오직 필요한 증가 (또는 감소)에 대해 푸는 것을 가능하게 만듭니다. 이 방법은 먼저, x_ext라고 부르는, 극값에서 x 값을 찾기 위해 미분을 사용합니다. 우리는 그런-다음 f(x_ext + q) = 0임을 보증하는 값, q에 대해 풉니다. 이것이 가장 직관적인 방법은 아니지만, 그것은 수학이 복잡하지 않은 것임을 보증합니다.

${\begin{aligned}f(x)&=ax^{2}+bx+c\\[5pt]{\frac {\partial f}{\partial x}}&=2ax+b\ \ .\end{aligned}}$

위의 미분을 영으로 설정함으로써 이차 함수의 극점을 우리에게 제공할 것입니다:

$x_{\text{ext}}={\frac {-b}{2a}}\ \ .$

우리는 다음으로 q를 정의합니다:

$q=x_{0}-x_{\text{ext}}\ \ ,$

여기서 x₀는 이차 방정식을 푸는 x의 값입니다. x_ext의 합과 관심의 변수 q는 다음 이차 방정식에 끼워 넣어집니다:

${\begin{aligned}a\left({\frac {-b}{2a}}+q\right)^{2}+b\left({\frac {-b}{2a}}+q\right)+c&=0\\[5pt]\left({\frac {-b}{2a}}+q\right)^{2}+{\frac {b}{a}}\left({\frac {-b}{2a}}+q\right)+{\frac {c}{a}}&=0&&(a\neq 0)\\[5pt]{\frac {b^{2}}{4a^{2}}}+q^{2}-{\frac {bq}{a}}-{\frac {b^{2}}{2a^{2}}}+{\frac {bq}{a}}+{\frac {c}{a}}&=0\\[5pt]{\frac {-b^{2}}{4a^{2}}}+q^{2}+{\frac {c}{a}}&=0\\[5pt]q^{2}&={\frac {b^{2}-4ac}{4a^{2}}}\\[5pt]q&={\frac {\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .\end{aligned}}$

극점에서 x의 값은 그런-다음 방정식의 양쪽 변에 더합니다:

$x_{0}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\ \ .$

이것은 이차 공식을 제공합니다. 이 방법은 제곱식을 완성하는 기법을 피하고 훨씬 더 복잡한 수학은 요구되지 않습니다.

By splitting into real and imaginary parts

Visualisation of the complex roots of y = ax² + bx + c: the parabola is rotated 180° about its vertex (orange). Its x-intercepts are rotated 90° around their mid-point, and the Cartesian plane is interpreted as the complex plane (green).

다음 방정식을 생각해 보십시오:

$az^{2}+bz+c=0,$

여기서 $z=x+iy$는 복소수이고, a, b, 및 c는 실수입니다. 그런 다음

${\begin{aligned}a(x+iy)^{2}+b(x+iy)+c&=0\\a(x^{2}-y^{2}+i2xy)+b(x+iy)+c&=0.\end{aligned}}$

이것은 두 방정식으로 분리하는데, 다음의 실수 부분:

$a(x^{2}-y^{2})+bx+c=0$

및 다음의 허수 부분입니다:

$2axy+by=0.$

$y\neq 0$임을 가정하고 y로 두 방정식을 나누면:

$2ax+b=0$

그리고 x에 대해 풀면:

$x={\frac {-b}{2a}}.$

x에 대해 이 값을 첫 번째 방정식에 치환하고 y에 대해 풀면:

${\begin{aligned}a\left({\frac {b^{2}}{4a^{2}}}-y^{2}\right)-{\frac {b^{2}}{2a}}+c&=0\\{\frac {b^{2}}{4a}}-ay^{2}-{\frac {2b^{2}}{4a}}+c&=0\\{\frac {-b^{2}}{4a}}-ay^{2}+c&=0\\ay^{2}+{\frac {b^{2}}{4a}}-c&=0\\y^{2}&={\frac {c}{a}}-{\frac {b^{2}}{4a^{2}}}\\y&=\pm {\sqrt {{\frac {c}{a}}-{\frac {b^{2}}{4a^{2}}}}}={\frac {\pm {\sqrt {ca-{\frac {b^{2}}{4}}}}}{a}}={\frac {\pm {\sqrt {4ca-b^{2}}}}{2a}}.\end{aligned}}$

$z=x+iy$이므로,

${\begin{aligned}z&={\frac {-b}{2a}}\pm {\frac {i{\sqrt {4ac-b^{2}}}}{2a}}\\[5pt]z&={\frac {-b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac}}{2a}}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.\end{aligned}}$

비록 y가 비-영임을 가정될지라도, 이 마지막 공식은 원래 방정식의 임의의 근에 대해 유지됩니다.

Historical development

이차 방정식을 푸는 가장 초기의 방법은 기하학적이었습니다. 바빌로니아 쐐기 태블릿은 이차 방정식을 풀기 위한 축소 가능한 문제를 포함합니다. 중세 왕국(Middle Kingdom) (기원전 2050년에서 기원전 1650년)으로 거슬러 올라가는, 이집트 베를린 파피루스(Berlin Papyrus)는 이-항 이차 방정식에 대한 해를 포함합니다.

Euclid in Raphael Sanzio's School of Athens

그리스의 수학자 유클리드 (기원전 약 300년)는 영향력있는 수학 논문, 그의 Elements의 제 2권에서 이차 방정식을 풀기 위한 기하학적 방법을 사용했습니다. 이차 방정식에 대해 규칙은 기원전 약 200년의 중국 The Nine Chapters on the Mathematical Art에서 나타납니다. 그의 작품 Arithmetica에서 그리스 수학자 디오판토스(Diophantus) (기원후 약 250년)는 유클리드의 기하학적 대수에 비해 보다 인식-가능한 대수적 방법과 함께 이차 방정식을 풀었습니다. 그의 해는, 심지어 두 근이 모두 양일 때에도, 오직 하나의 근을 제공합니다.

인도의 수학자 브라마굽타(Brahmagupta) (기원후 597–668)는 기원후 628년에 출판된 그의 논문 Brāhmasphuṭasiddhānta에서 이차 공식을 명시적으로 설명했지만, 기호 대신에 단어로 쓰였습니다. 이차 방정식 ax² + bx = c의 그의 해는 다음이었습니다: "절대 숫자에 제곱[의 계수]의 네 배를 곱한 후에, 중간 항[의 계수]의 제곱을 더합니다; 그 숫자의 제곱근, 중간 항[의 계수]을 빼십시오, 제곱[의 계수] 두 배로 나누면 그 값입니다." 이것은 다음과 동등합니다:

$x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}\ \ .$

9세기 페르시아 수학자 무하마드 이븐 무사 알-콰리즈미(Muḥammad ibn Mūsā al-Khwārizmī)는 대수적으로 이차 방정식을 풀었습니다. 모든 경우를 포괄하는 이차 공식은 1594년에 시몬 스테빈(Simon Stevin)에 의해 처음으로 획득되었습니다. 1637년에 르네 데카르트(René Descartes)는 오늘날 우리가 알고 있는 형식으로 이차 공식의 특수한 경우를 포함하는 La Géométrie를 출판했습니다. 현대 수학적 문헌에서 일반적인 해의 첫 번째 출현은 헨리 히튼(Henry Heaton)에 의한 1896년 논문에서 나타났습니다.

Significant uses

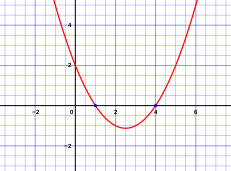
Geometric significance

Graph of y = ax² + bx + c, where a and the discriminant b² − 4ac are positive, with

• Roots and y-intercept in red
• Vertex and axis of symmetry in blue
• Focus and directrix in pink

좌표 기하학의 관점에서, 포물선은 (x, y)-좌표가 이차 다항식, 즉 다음 형식의 임의의 방정식으로 묘사되는 곡선입니다:

$y=p(x)=a_{2}x^{2}+a_{1}x+a_{0}\ \ ,$

여기서 p는 차수 2의 다항식을 나타내고 a₀, a₁, 및 a₂ ≠ 0는 아래첨자가 그들이 나타내는 항의 차수에 해당하는 상수 계수입니다. 이차 공식의 기하학적 해석은, 그것이 x-축 위의 점을 정의한다는 것이며 여기서 포물선은 축을 가로지를 것입니다. 추가적으로, 만약 이차 공식이 다음 두 항으로 보이면,

$x={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}$

대칭의 축(axis of symmetry:대칭축)은 직선 x = −b/2a으로 나타납니다. 다른 항, √b² − 4ac/2a은 대칭의 축으로부터 떨어져있는 영들의 거리를 제공하며, 여기서 양의 부호는 오른쪽에 대한 거리를 나타내고, 음의 부호는 왼쪽에 대한 거리를 나타냅니다.

만약 이 거리 항이 영으로 줄어들면, 대칭축의 값은 유일한 영의 x 값일 것입니다. 즉, 이차 방정식에 대한 유일한 하나의 가능한 해입니다. 대수적으로, 이것은 √b² − 4ac = 0, 또는 간단히 b² − 4ac = 0임을 의미합니다 (여기서 왼쪽 변은 판별식으로 참조됩니다). 이것은 세 경우의 하나이며, 여기서 판별식은 포물선이 얼마나 많은 영들을 가질 수 있는지를 나타냅니다. 만약 판별식이 양수이면, 거리는 비-음일 것이고, 두 개의 해가 있을 것입니다. 어쨌든, 판별식이 영보다 작은 경우가 역시 있고, 이것은 거리가 허수 (또는 허수 단위 i의 어떤 배수, 여기서 i = √−1입니다)일 것이고 포물선의 영은 복소수(complex number)일 것입니다. 복소수 근은 복소수 켤레(complex conjugate)일 것이며, 여기서 복소수 근의 실수 부분은 대칭축의 값일 것입니다. 포물선이 x-축을 가로지르는 x의 실수 값이 없을 것입니다.

Dimensional analysis

만약 상수 a, b, 및/또는 c가 무단위(unitless)가 아니면, x의 단위는, ax²와 bx가 그들의 단위와 일치한다는 요구사항에 기인하여, b/a의 단위에 반드시 같아야 합니다. 게다가, 같은 논리에 의해, c의 단위는 b²/a의 단위와 반드시 같아야 하며, 이것은 x에 대해 푸는 것없이 검증될 수 있습니다. 이것은, 물리적 양(physical quantities)의 이차 표현이, 이것을 풀기 전에, 정확하게 설정되어 왔는지 검증하는 것에 대해 강력한 도구일 것입니다.

See also

• Discriminant
• Fundamental theorem of algebra
• Cubic equation