Rotation

A sphere rotating (spinning) about an axis

회전(rotation)은 회전의 축(axis of rotation)을 중심으로 한 대상의 원형 운동입니다. 삼-차원 대상은 무한대의 회전축을 가질 수 있습니다.

만약 회전 축이 몸체 자체의 질량의 중심(center of mass)을 내부로 통과하면, 그 몸체는 자동회전(autorotating) 또는 스피닝(spinning)으로 말해지고, 축의 표면 교차는 극(pole)이라고 불릴 수 있습니다. 완전히 외부 축을 중심으로 한 회전, 예를 들어, 태양(Sun) 주위를 도는 행성 지구(Earth)는 전형적으로 그것이 중력(gravity)에 의해 생성될 때 자전(revolving) 또는 공전(orbiting)이라고 불리고, 회전축의 끝은 궤도 극(orbital pole)이라고 불릴 수 있습니다.

Mathematics

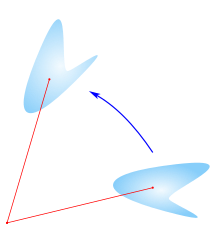
Relations between rotation axis, plane of orbit and axial tilt (for Earth).

수학적으로(Mathematically), 회전은 평행이동(translation)과 달리 한 점을 고정된 상태로 유지하는 강체(rigid body) 운동입니다. 이 정의는 이-차원과 삼-차원 (각각 평면과 공간) 내 회전에 적용됩니다.

모든 강체 운동은 회전, 평행이동, 또는 그 둘의 조합입니다.

회전은 단순히 공통 점에 대한 점진적인 방사형 방향입니다. 해당 공통 점은 해당 움직임의 축 안에 놓입니다. 그 축은 운동의 평면에 수직으로 90도입니다. 만약 회전의 축이 질문에서 몸체의 외부에 놓이면 그 몸체는 궤도를 도는 것이라고 말합니다. "회전"과 "궤도" 및/또는 "스핀" 사이는 근본적인 차이가 없습니다. 주요 차이점은 단순히 회전의 축이 질문에서 몸체 내부 또는 외부에 놓이는 위치에 있습니다. 이 구별은 "강체" 및 "비강체" 모두에 대해 시연될 수 있습니다.

만약 한 점이나 축을 중심으로 한 회전에 이어 같은 점/축을 중심으로 한 두 번째 회전이 발생하면, 세 번째 회전이 발생합니다. 회전의 반대 (역(inverse))은 역시 회전입니다. 따라서, 점/축을 중심으로 한 회전은 그룹(group)을 형성합니다. 어쨌든, 점 또는 축을 중심으로 한 회전과 다른 점/축을 중심으로 한 회전은 회전이 아닌 다른 결과, 예를 들어 평행이동을 초래할 수 있습니다.

x, y, 및 z 축을 중심으로 한 회전은 주요 회전(principal rotations)이라고 불립니다. 임의의 축을 중심으로 한 회전은 x축을 중심으로 회전한 다음, y축을 중심으로 회전한 다음, z축을 중심으로 회전하여 수행될 수 있습니다. 다시 말해서, 임의의 공간 회전은 주요 회전의 조합으로 분해될 수 있습니다.

비행 동역학(flight dynamics)에서, 주요 회전(principal rotations)은 요(yaw), 피치(pitch), 및 롤(roll)로 알려져 있습니다 (테이트–브라이언 각도(Tait–Bryan angles)로 알려져 있습니다). 이 용어는 역시 컴퓨터 그래픽(computer graphics)에서 사용됩니다.

Astronomy

천문학(astronomy)에서, 회전은 공통적으로 관찰되는 현상입니다. 별(star), 행성(planet), 및 이와 유사한 천체는 모두 그것들의 축을 중심으로 회전합니다. 태양 시스템에서 행성의 회전 율은 먼저 시각적 특징을 추적함으로써 측정되었습니다. 항성 회전(Stellar rotation)은 도플러 이동(Doppler shift)을 통해 또는 활성 표면 특징을 추적함으로써 측정됩니다.

이 회전은 적도(equator)에 가까울수록 중력(gravitation)의 영향을 약간 상쇄하는 지구의 기준 좌표계에서 원심 가속도(centrifugal acceleration)를 유도합니다. 지구의 중력(Earth's gravity)은 물체의 무게가 극에서 보다 적도에서 약간 더 작음을 만족하는 두 가지 질량 효과를 결합합니다. 또 다른 것은 시간이 지남에 따라 지구가 약간 편평한 타원체(oblate spheroid)로 변형된다는 것입니다; 비슷한 적도 돌출부(equatorial bulge)가 다른 행성에서도 발생합니다.

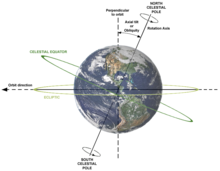
행성의 자전의 또 다른 결과는 세차운동(precession)의 현상입니다. 자이로스코프(gyroscope)와 마찬가지로, 전체적인 효과는 행성의 축의 움직임에서 약간의 "흔들림"입니다. 현재 지구(Earth) 축의 궤도면에 대한 경사 (황도의 경사도(obliquity of the ecliptic))는 23.44 도이지만, 이 각도는 (수천 년에 걸쳐) 천천히 변합니다. (역시 춘분의 세차운동(Precession of the equinoxes) 및 극 별(Pole star)을 참조하십시오.)

Revolution

공전은 종종 회전에 대해 동의어로 사용되지만, 많은 분야, 특히 천문학과 관련 분야에서, 공전은, 명확성을 위해 종종 궤도 회전으로 참조되며, 한 전체가 또 다른 전체 주위를 이동할 때 사용되고 반면에 회전은 축 주위의 움직임을 의미하기 위해 사용됩니다. 달은 그것들의 행성을 중심으로 공전하고, 행성은 그것들 별을 중심으로 공전합니다 (예를 들어 태양 주위의 지구); 그리고 별은 그것들의 은하 중심(galaxial center)을 중심으로 천천히 공전합니다. 은하(galaxies)의 구성 요소의 움직임은 복잡하지만, 보통 회전 구성 요소를 포함합니다.

Retrograde rotation

지구(Earth)를 포함한 태양 시스템(Solar System)에서 대부분의 행성(planet)은 그것들이 태양(Sun)을 공전할 때 같은 방향으로 자전합니다. 금성(Venus)과 천왕성(Uranus)은 예외입니다. 금성은 천천히 뒤로 회전하는 (또는 "거꾸로" 회전하는) 것으로 생각될 수 있습니다. 천왕성은 그것의 궤도에 관해 거의 옆으로 회전합니다. 현재 추측에 따르면 천왕성은 전형적인 프로그레이드 방향으로 시작했고 역사상 초기에 큰 충격으로 인해 옆으로 쓰러졌습니다. 왜행성(dwarf planet) 명왕성(Pluto) (이전에는 행성으로 고려됨)은 옆으로 회전한다는 점을 포함하여 여러 면에서 변칙적입니다.

Physics

회전의 속도(speed of rotation)는 각도 주파수(angular frequency) (rad/s) 또는 주파수(frequency) (시간당 바퀴(turns)), 또는 기간(period) (초, 일, 등)에 의해 제공됩니다. 각도 주파수의 변화 시간-율은 토크(torque)로 인한 각도 가속도 (rad/s²)입니다. 그 둘의 비율 (시작, 중지, 또는 그렇지 않으면 회전의 변경이 얼마나 강한지)은 관성 모멘트(moment of inertia)에 의해 제공됩니다.

각속도(angular velocity) 벡터 (축 벡터(axial vector))는 역시 회전의 축의 방향을 나타냅니다. 유사하게 토크는 축 벡터입니다.

고정된 축을 중심으로 한 회전(rotation around a fixed axis)의 물리학은 회전의 축–각도 표시(axis–angle representation)로 수학적으로 설명됩니다. 오른-손 법칙(right-hand rule)에 따르면, 관찰자로부터 멀어지는 방향은 시계-방향 회전과 결합되고 관찰자를 향하는 방향은 나사(screw)처럼 반시계 방향 회전으로 결합됩니다.

Cosmological principle

물리의 법칙(laws of physics)은 현재 임의의 고정된 회전 아래에서 불변으로 믿어집니다. (비록 그것들이 회전하는 관점에서 보일 때 변경되는 것처럼 보일지라도: 회전하는 참조 프레임(rotating frame of reference)을 참조하십시오.)

현대 물리 우주론에서, 우주론적 원리(cosmological principle)는, 힘이 우주 전체에 균등하게 작용할 것으로 예상되고 선호하는 방향을 가지지 않고, 따라서 빅뱅에 의해 처음에 정해진 물질 필드의 진화 과정에 걸쳐 대규모 구조화에서 관찰-가능 불규칙성을 일으키지 않기 때문에, 우주의 물질 분포가 충분하게 큰 스케일로 보일 때 균일(homogeneous)하고 등방적(isotropic)이라는 개념입니다.

특히, 그것이 공간에서 방향화된 방법에 관계없이 같은 것이 행동하는 시스템에 대해, 그것의 라그랑주(Lagrangian)는 회전적으로 불변입니다. 뇌터의 정리(Noether's theorem)에 따르면, 만약 물리적 시스템의 작용 (그것의 라그랑주의 시간에 걸쳐 적분(integral over time))이 회전 아래에서 불변이면, 각도 운동량은 보존됩니다.

Euler rotations

오일러 회전은 회전의 대안적인 설명을 제공합니다. 그것은 오일러 각도(Euler angles) 중 하나를 변경하고 나머지 둘은 상수로 남겨둠으로써 얻어진 움직임으로 정의되는 세 회전의 합성입니다. 오일러 회전은 외부 프레임의 관점에서, 또는 함께 움직이는 회전된 몸체 프레임의 관점에서 결코 표현되지 않고 혼합으로 표현됩니다. 그것들은 회전 시스템의 혼합된 축을 구성하며, 여기서 첫 번째 각도는 외부 축 z를 중심으로 노드의 선(line of nodes)을 이동하고, 두 번째 각도는 노드의 선(line of nodes)을 중심으로 회전하고, 세 번째 각도는 움직이는 몸체에 고정된 축을 중심으로 한 고유 회전입니다.

이들 회전은 세차(precession), 장동(nutation), 및 고유 회전이라고 불립니다.

Flight dynamics

비행 동역학(flight dynamics)에서, 위의 오일러 각도로 설명된 주요 회전은 피치, 롤, 및 요로 알려져 있습니다. 회전(rotation)이라는 용어는 특히 이륙 후 상승을 시작할 때 항공기의 상향 피치 (기수가 위로 이동함)를 참조하기 위해 항공에서도 사용됩니다.

주요 회전은 짐벌(gimbal), 및 조이스틱(joystick)과 같은 여러 물리적 시스템을 모델링하는 이점을 가지므로, 쉽게 시각화되고, 회전을 저장하는 매우 간결한 방법입니다. 그러나 그것들은 회전 조합과 같은 간단한 작업도 수행하는 데 계산에서 사용하기 어렵고, 각도가 특정 회전에 대해 고유하게 계산될 수 없는 짐벌 잠금(gimbal lock)의 형식으로 고통을 받습니다.

Amusement rides

많은 놀이기구(amusement ride)는 회전을 제공합니다. 관람차(Ferris wheel)는 중력에 의해 또는 기계적으로 회전이 반대인 각 곤돌라에 대해 수평 중심축과 평행 축을 가지고 있습니다. 결과로써, 곤돌라의 방향은 언제든지 수직 (회전하지 않음)이며, 단지 평행이동됩니다. 평행이동 벡터의 끝은 원을 나타냅니다. 회전목마는 수직 축에 대한 회전을 제공합니다. 많은 놀이기구는 여러 축에 대한 회전 조합을 제공합니다. Chair-O-Planes에서, 수직축에 대한 회전은 기계적으로 제공되고, 반면에 수평 축에 대한 회전은 구심력(centripetal force)으로 인한 것입니다. 롤러 코스터 역전(roller coaster inversion)에서 수평 축에 대한 회전은 하나 이상의 전체 사이클이며, 여기서 관성은 사람들을 좌석에 유지시킵니다.

Sports

보통 스핀이라고 불리는 공 또는 다른 물체의 회전은 테니스(tennis)에서 탑스핀과 백스핀, 당구에서 들어치기(English), 밀어치기(follow), 및 끌어치기(draw), 야구에서 커브 볼, 크리켓에서 스핀 볼링, 플라잉 디스크 스포츠, 등을 포함해서 많은 스포츠에서 중요한 역할을 합니다. 탁구 채는 플레이어에게 공에 더 많거나 적은 양의 스핀을 부여할 수 있도록 다른 표면 특성으로 제조됩니다.

선수가 수직축을 중심으로 한 번 이상 회전은 피겨 스케이팅에서 스핀, 배턴 트위링에서 (배턴 또는 연주자의) 트위링, 또는 스노보딩에서 360, 540, 720 등, 기타 등등이라고 불릴 수 있습니다. 선수 또는 연주자의 수평 축을 중심으로 한 번 이상의 회전은 체조, 수상 스키, 또는 많은 다른 스포츠에서 플립, 롤, 공중제비, 헬리 등, 또는 다이빙에서 한번-반, 두번-반, 게이너 (물과 반대 방향으로 시작) 등, 기타 등등으로 불릴 수 있습니다. 수직과 수평 회전의 조합 (360° 백 플립)은 수상스키 자유형 점프에서 뫼비우스라고 불립니다.

일반적으로 180도에서 360도 사이의 수직 축을 중심으로 선수의 회전은 스핀 이동이라고 불릴 수 있고, 기만 또는 회피 기동으로 사용되거나, 볼 또는 퍽을 플레이, 패스, 또는 받는 등, 또는 플레이어에게 골 또는 다른 플레이어의 시야를 제공 위한 시도로 사용됩니다. 그것은 종종 하키, 농구, 다양한 코드의 축구, 테니스 등에서 볼 수 있습니다.

Fixed axis vs. fixed point

고정된 점에 대한 3D에서 임의의 물체의 회전의 임의의 순서의 최종 결과는 항상 한 축에 대한 회전과 동등합니다. 어쨌든, 물체는 동시에 둘 이상의 축에서 고정된 점에 대한 3D에서 물리적으로 회전할 수 있으며, 이 경우에서 단일 고정된 회전의 축이 없습니다 – 단지 고정된 점이 있습니다. 어쨌든, 이들 두 가지 설명은 조화될 수 있습니다 – 그러한 물리적 운동은 항상 단일 회전의 축의 관점에서 다시 설명될 수 있으며, 물체에 관한 해당 축의 방향이 시시각각 변할 수 있다는 조건 아래에서 그렇습니다.

Axis of 2 dimensional rotations

2-차원 회전은, 3-차원 회전과 달리, 회전축이 없습니다. 이것은 선형 변환에 대해 동등하며, 물론 동일성을 제외하고는 2-차원 회전에 의해 변경되지 않고 유지되는 위치에 방향이 없다는 것과 같습니다.

그러한 방향의 존재에 대한 질문은 회전을 나타내는 행렬 A에 대해 고유벡터(eigenvector)의 존재에 대한 질문입니다. 반시계 방향에서 각도 $\theta$ 를 통한 원점 주위의 모든 각 2D 회전은 다음 행렬에 의해 아주 간단하게 표현될 수 있습니다:

A={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}

표준 고윳값(eigenvalue) 결정은 특성 방정식(characteristic equation)으로 이어집니다:

\lambda ^{2}-2\lambda \cos \theta +1=0

,

이것은 그것의 고윳값으로 다음을 가집니다:

\cos \theta \pm i\sin \theta

.

그러므로, $\cos \theta \neq \pm 1$ 일 때마다 실수 고윳값은 없으며, 이것은 평면에 실수 벡터가 A에 의해 변경되지 않은 상태로 유지되지 않음을 의미합니다.

Rotation angle and axis in 3 dimensions

자취가 불변임을 알면, 적절한 직교 3x3 회전 행렬 $A$ 에 대해 회전 각도 $\alpha$ 다음에 의해 구해집니다:

\alpha =\cos ^{-1}\left({\frac {A_{11}+A_{22}+A_{33}-1}{2}}\right)

주요 아크-코사인을 사용하여, 이 공식은 $0\leq \alpha \leq 180^{\circ }$ 를 만족시키는 회전 각도를 제공합니다. 해당하는 회전 축은 회전 각도를 180도를 초과하지 않도록 제한하는 방향에서 가르키기 위해 정의되어야 합니다. (이것은 축 $m$ 에 대한 180 각도 이상의 임의의 회전은 만약 그 축이 $n=-m$ 으로 대체되면 $0\leq \alpha \leq 180^{\circ }$ 을 가지는 회전으로 쓸 수 있기 때문에 항상 수행될 수 있습니다.)

3D 공간에서 모든 각 적절한 회전 $A$ 는 회전 축을 가지며, 회전 축과 정렬된 임의의 벡터 $v$ 는 회전에 의해 영향을 받지 않음을 만족하도록 정의됩니다. 그것에 따라서, $Av=v$ 이고, 회전 축은 따라서 고윳값 1과 결합된 회전 행렬의 고유벡터에 해당합니다. 회전 각도 $\alpha$ 가 비-영인 한 (즉, 회전이 항등 텐서가 아닌 한), 그러한 방향은 단 하나뿐입니다. $A$ 가 오직 실수 성분을 가지기 때문에, 적어도 하나의 실수 고윳값이 있고, 남아있는 두 고윳값은 서로의 복소 켤레여야 합니다 (Eigenvalues and eigenvectors#Eigenvalues and the characteristic polynomial를 참조하십시오). 1이 고윳값임을 알면, 남아있는 두 고윳값은 서로의 복소 켤레이지만, 이것이 그것들이 복소수를 의미하는 것은 아님–그것들은 이중 중복도를 갖는 실수일 수 있음을 따릅니다. 회전 각도 $\alpha =180^{\circ }$ 의 축퇴 경우에서, 남아있는 두 고윳값은 모두 −1과 같습니다. 영 회전 각도의 퇴화 경우에서, 회전 행렬은 항등이고, 모든 셋의 고윳값은 1입니다 (이것은 회전 축이 임의적이라는 유일한 경우입니다).

스펙트럼 분석은 회전 축을 찾기 위해 요구되지 않습니다. 만약 $n$ 이 회전 축에 정렬된 단위 고유벡터를 나타내고, $\alpha$ 가 회전 각도를 나타내면, $2\sin(\alpha )n=\{A_{32}-A_{23},A_{13}-A_{31},A_{21}-A_{12}\}$ 임을 보일 수 있습니다. 결과적으로, 고윳값 분석의 비용은 만약 그것이 비-영 크기를 가지면 이 벡터를 단순히 정규화함으로써 피해질 수 있습니다. 다시 말해서, 이 벡터가 영일 것과 회전 각도가 0 또는 180 각도인 것은 필요충분 조건이고, 회전 축은 비-영 크기를 가지는 $A+I$ 의 임의의 열을 정규화함으로써 이 경우에서 할당될 수 있습니다.^[2]

이 논의는 적절한 회전에 적용되고, 따라서 $\det A=1$ 입니다. 임의의 부적절한 직교 3x3 행렬 $B$ 는 $B=-A$ 로 쓸 수 있으며, 이것에서 $A$ 는 적절한 직교입니다. 즉, 임의의 부적절한 직교 3x3 행렬은 적절한 회전 (위에서 설명한 대로 회전 축을 찾을 수 있음)에 뒤이은 반전 (−1에 의한 곱셈)으로 분해될 수 있습니다. $A$ 의 회전 축은 역시 고윳값 −1에 해당하는 $B$ 의 고유벡터임을 따릅니다.

Rotation plane

모든 각 삼차원 회전이 회전 축을 가지는 것처럼, 역시 모든 각 삼차원 회전은 회전 축에 수직이고 회전에 의해 불변으로 남겨지는 한 평면을 가집니다. 이 평면으로 제한된 회전은 보통의 2D 회전입니다.

증명은 위의 논의와 유사하게 진행됩니다. 먼저, 3D 회전 행렬 A의 모든 고윳값이 실수라고 가정합니다. 이것은 대응하는 고유벡터 (필연적으로 직교해야 함)에 의해 만들어진 직교 기저가 있다는 것을 의미하며, 회전 행렬의 효과는 단지 그것을 늘리는 것입니다. 만약 우리가 이 기저로 A를 쓰면, 그것은 대각선입니다; 그러나 대각 직교 행렬은 대각선 엔트리에서 +1과 −1만으로 구성됩니다. 그러므로, 우리는 적절한 회전이 없지만, 일련의 반사 결과 또는 항등을 가지고 있습니다.

그런-다음, 적절한 회전은 일부 복소 고윳값을 가짐을 따릅니다. v를 해당하는 고유벡터라고 놓습니다. 그런-다음, 우리는 이전 주제에서 보여주었듯이, ${\bar {v}}$ 는 역시 고유벡터이고, $v+{\bar {v}}$ 와 $i(v-{\bar {v}})$ 는 그것들의 스칼라 곱이 사라짐을 만족하는 것입니다.

i(v^{T}+{\bar {v}}^{T})(v-{\bar {v}})=i(v^{T}v-{\bar {v}}^{T}{\bar {v}}+{\bar {v}}^{T}v-v^{T}{\bar {v}})=0

왜냐하면, ${\bar {v}}^{T}{\bar {v}}$ 가 실수이므로, 그것은 복소 켤레 $v^{T}v$ 와 같고, ${\bar {v}}^{T}v$ 와 $v^{T}{\bar {v}}$ 는 둘 다 $v$ 와 ${\bar {v}}$ 사이의 같은 스칼라 곱의 표시입니다.

이것은 $v+{\bar {v}}$ 와 $i(v-{\bar {v}})$ 는 직교 벡터임을 의미합니다. 역시, 그것들은 둘 다 구성에 의한 실수 벡터입니다. 이들 벡터는 $v$ 와 ${\bar {v}}$ 와 같은 부분공간을 확장하며, 이것은 A의 적용 아래에서 불변 부분공간입니다. 그러므로, 그것들은 불변 평면을 확장합니다.

이 평면은 A의 고유벡터의 직교성 때문에 고윳값 1을 갖는 A의 남아있는 고유벡터에 해당하는 불변 축에 직교합니다.

References

^ "An Oasis, or a Secret Lair?". ESO Picture of the Week. Archived from the original on 11 October 2013. Retrieved 8 October 2013.
^ Brannon, R.M., "Rotation, Reflection, and Frame Change", 2018

External links

"Rotation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Product of Rotations at cut-the-knot. cut-the-knot.org
When a Triangle is Equilateral at cut-the-knot. cut-the-knot.org
Rotate Points Using Polar Coordinates, howtoproperly.com
Rotation in Two Dimensions by Sergio Hannibal Mejia after work by Roger Germundsson and Understanding 3D Rotation by Roger Germundsson, Wolfram Demonstrations Project. demonstrations.wolfram.com
Rotation, Reflection, and Frame Change: Orthogonal tensors in computational engineering mechanics, IOP Publishing

[1] "An Oasis, or a Secret Lair?". ESO Picture of the Week. Archived from the original on 11 October 2013. Retrieved 8 October 2013.

[2] Brannon, R.M., "Rotation, Reflection, and Frame Change", 2018

[1]

[2]