Rotation (mathematics)

수학(mathematics)에서, 회전은 기하학(geometry)에서 기원하는 개념입니다. 임의의 회전은 적어도 하나의 점(point)을 보존하는 특정 공간(space)의 운동(motion)입니다. 그것은, 예를 들어, 고정된 점을 중심으로 강체(rigid body)의 운동을 설명할 수 있습니다. 회전은 (각도의 부호에서 처럼) 부호(sign)를 가질 수 있습니다: 시계방향 회전은 음의 크기이므로 반시계방향 회전은 양의 크기를 가집니다. 회전은 운동의 다른 유형과 다릅니다: 고정 점을 가지지 않는 평행이동(translations), 및 (초평면) 반사(reflections), 그들의 각각은 $n$ -차원(dimensional) 공간에서 고정 점의 전체 $(n - 1)$ -차원 플랫(flat)을 가집니다.

수학적으로, 회전은 맵(map)입니다. 고정된 점에 대한 모든 회전은 (특정 공간의) 회전 그룹(rotation group)이라고 불리는 합성(composition) 아래에서 그룹(group)을 형성합니다. 그러나 역학(mechanics) 및, 더 일반적으로, 물리학(physics)에서, 이 개념은 좌표 변환(coordinate transformation) (중요하게, 직교-정규 기저(orthonormal basis)의 변환)으로 자주 이해되는데, 왜냐하면 몸체의 임의의 운동에 대해, 만약 같은 좌표에 있는 물체의 결과로 참조 프레임(frame of reference)에 적용되면 역 변환이 있기 때문입니다. 예를 들어, 이차원에서 고정된 축을 유지하는 점에 대한 시계 방향(clockwise)으로 몸체를 회전하는 것은 몸체가 고정되게 유지되고 같은 점에 대한 반시계방향으로 축을 회전하는 것과 동등합니다. 이들 회전의 두 유형은 능동과 수동 변환(active and passive transformation)이라고 불립니다.^[1]^[2]

Related definitions and terminology

회전 그룹(rotation group)은 고정된 점(fixed point)에 대한 회전의 리 그룹(Lie group)입니다. 이 (공통) 고정된 점은 회전의 중심이라고 불리고 보통 원점(origin)으로 식별됩니다. 회전 그룹은 운동(motions)의 (방향-보존하는) 더 넓은 그룹에서 점 안정기입니다.

특정 회전에 대해:

회전의 축은 그것의 고정된 점의 직선(line)입니다. 그것들은 $n > 2$ 에서 오직 존재합니다.
회전의 평면은 회전 아래에서 불변(invariant)인 평면(plane)입니다. 축과 달리, 그것의 점은 자체로 고정되지 않습니다. 회전의 축 (존재하는 곳)과 평면은 직교(orthogonal)합니다.

회전의 표시는 회전 맵을 매개변수화하기 위해 사용되는 대수적 또는 기하학적 특정 형식주의입니다. 이 의미는 어떻게 든 그룹 이론에서 의미와 반대입니다.

점의 (아핀) 공간과 각각의 벡터 공간(vector space)의 회전이 항상 명확하게 구별되는 것은 아닙니다. 전자는 때때로 아핀 회전으로 참조되고 (비록 그 용어가 오해의 소지가 있을지라도), 반면에 후자는 벡터 회전입니다. 자세한 내용에서 아래 기사를 참조하십시오.

Definitions and representations

In Euclidean geometry

A plane rotation around a point followed by another rotation around a different point results in a total motion which is either a rotation (as in this picture), or a translation.

유클리드 공간(Euclidean space)의 운동은 그것의 등거리변환(isometry)과 같습니다: 그것은 변환 후 임의의 두 점 사이의 거리(distance)를 변경하지 않고 그대로 둡니다. 그러나 (적절한) 회전은 역시 방향 구조(orientation structure)를 보존해야 합니다. "부적절한 회전(improper rotation)"이라는 용어는 방향을 뒤집는 등거리변환을 참조합니다. 그룹 이론(group theory)의 언어에서 구별은 유클리드 그룹(Euclidean group)에서 직접 대 간접 등거리변환으로 표현되며, 여기서 전자는 항등 구성요소(identity component)를 구성합니다. 임의의 직접적인 유클리드 운동은 고정된 점에 대한 회전과 평행이동의 조합으로 나타낼 수 있습니다.

일-차원에서 비-자명한(trivial) 회전은 없습니다. 이-차원(two dimensions)에서, 오직 단일 각도(angle)가 원점(origin)에 대한 회전을 지정하기 위해 필요됩니다 – 원 그룹(circle group)의 원소를 지정하는 회전의 각도 (역시 $U(1)$ 으로 알려져 있음)입니다. 그 회전은 원점(origin)에 대한 각도 $θ$ 만큼 대상을 반시계방향(counterclockwise)으로 회전시키는 역할을 합니다; 자세한 내용은 아래를 참조하십시오. 회전의 합성은 그것의 각도 모듈로(modulo) 1 바퀴(turn)로 합산하며, 이것은 같은 점에 대한 모든 이-차원 회전이 교환(commute)된다는 것을 의미합니다. 다른 점에 대한 회전은, 일반적으로, 교환되지 않습니다. 임의의 이-차원 직접 운동은 평행이동 또는 회전입니다; 자세한 내용에 대해 유클리드 평면 등거리변환(Euclidean plane isometry)을 참조하십시오.

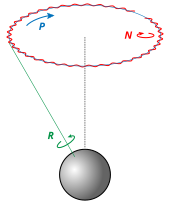
Euler rotations of the Earth. Intrinsic (green), precession (blue) and nutation (red)

삼-차원 공간(three-dimensional space)에서 회전은 여러 가지 중요한 면에서 이-차원에서의 회전과 다릅니다. 삼-차원에서 회전은 일반적으로 교환적(commutative)이 아니므로, 회전이 적용되는 순서가 심지어 같은 점에 대해서도 중요합니다. 역시, 이-차원의 경우와 달리, 삼-차원 직접 운동은, 일반적인 위치(general position)에서, 회전이 아닌 나사 조작(screw operation)입니다. 원점에 대한 회전은 차원의 숫자와 같은 셋의 자유도를 가집니다 (자세한 내용에 대해 삼차원에서 회전 형식주의(rotation formalisms in three dimensions)를 참조하십시오).

삼-차원 회전은 여러 가지 방법으로 지정될 수 있습니다. 가장 보통의 방법은 다음입니다:

오일러 각도(Euler angles) (왼쪽에 있는 그림). 원점에 대한 임의의 회전은 오일러 각도 중 하나를 변경하고 나머지 둘을 상수로 남겨둠으로써 얻어진 운동으로 정의된 세 회전의 합성(composition)으로 나타낼 수 있습니다. 그것들은 회전 시스템의 혼합된 축을 구성하는데 왜냐하면 각도는 순수하게 외부적이거나 순수하게 고유한 단일 프레임이 아니라 서로 다른 참조 프레임(reference frames)의 혼합과 관련하여 측정되기 때문입니다. 구체적으로 특별히, 첫 번째 각도는 외부 축 z를 중심으로 노드의 선(line of nodes)을 이동하고, 두 번째 각도는 노드의 선을 중심으로 회전하고 세 번째 각도는 움직이는 몸체에 고정된 축을 중심으로 한 고유 회전 (스핀)입니다. 오일러 각도는 전형적으로 α, β, γ, 또는 φ, θ, ψ로 표시됩니다. 이 표시는 고정된 점에 대한 회전에 대해 오직 편리합니다.

축–각도 표시(axis–angle representation) (오른쪽에 있는 그림)는 회전이 발생하는 축과의 각도를 지정합니다. 그것은 쉽게 시각화될 수 있습니다. 그것을 나타내기 위한 두 가지 변형이 있습니다:
- 각도와 축에 대해 단위 벡터(unit vector)로 구성된 쌍으로, 또는
- 각도에, 회전 벡터로 불리는, 이 단위 벡터를 곱함으로써 얻어진 유클리드 벡터(Euclidean vector)로 (비록, 엄밀하게 말하면, 그것은 유사-벡터(pseudovector)이지만).
행렬, 버서 (쿼터니언), 및 다른 대수적 항목: 자세한 내용에 대해 선형 및 다중-선형 대수 형식주의 섹션을 참조하십시오.

A perspective projection onto three-dimensions of a tesseract being rotated in four-dimensional Euclidean space.

사-차원(four dimensions)에서 일반적인 회전은 오직 하나의 고정된 점, 회전의 중심을 가지고, 회전의 축은 없습니다; 자세한 내용에 대해 4-차원 유클리드 공간에서 회전을 참조하십시오. 대신 회전이 서로 직교하는 둘의 회전 평면이 있으며, 이것의 각각이 각 평면에서 점이 평면 내에 유지된다는 점에서 고정되어 있습니다. 그 회전은 각 회전 평면에 대해 하나씩 둘의 회전의 각도를 가지며, 평면에서 점이 회전합니다. 만약 이것들이 $ω 1$ 과 $ω 2$ 이면 평면에 있지 않은 모든 점은 $ω 1$ 과 $ω 2$ 사이의 각도로 회전합니다. 고정된 점에 대한 사-차원에서 회전은 여섯 자유도를 가집니다. 일반적인 위치에서 사-차원 직접 운동은 특정 점에 대한 회전 (모든 짝수(even) 유클리드 차원에서와 같이)이지만, 나사 조작도 존재합니다.

Linear and multilinear algebra formalism

우리가 그 원점(the origin)을 유지하는 유클리드 공간의 운동을 고려할 때, 순수 수학에서 중요한 점과 벡터 사이의 구분이 지워질 수 있는데 왜냐하면 점과 위치 벡터(position vectors) 사이에 정식의 일-대-일 대응(one-to-one correspondence)이 있기 때문입니다. 같은 것은 유클리드(Euclidean) 이외의 기하학에 대해 참이지만, 그것의 공간은 보충 구조(structure)를 갖는 아핀 공간(affine space)입니다; 아래의 예제를 참조하십시오. 대안적으로, 회전의 벡터 설명은 평행이동을 갖는 그것들의 합성까지(up to) 기하학적 회전의 매개변수화로 이해될 수 있습니다. 다시 말해서, 하나의 벡터 회전은 공간에서 모든 점에 대한 많은 동등한 회전을 나타냅니다.

원점을 유지하는 운동은 같은 기하학적 구조를 유지하지만 벡터의 관점에서 표현되는 벡터의 선형 연산자(linear operator)와 같습니다. 유클리드 벡터(Euclidean vector)에 대해, 이 표현은 그것들의 크기 (유클리드 노름(Euclidean norm))입니다. 구성요소(components)에서, 그러한 연산자는 열 벡터(column vector)로 곱해지는 $n \times n$ 직교 행렬(orthogonal matrix)로 표현됩니다.

이미 언급했듯이, (적절한) 회전은 벡터 공간의 방향의 그것의 보존에서 임의적인 고정된-점 운동과 다릅니다. 따라서, 회전 직교 행렬의 행렬식(determinant)은 1이어야 합니다. 직교 행렬의 행렬식에 대해 유일한 다른 가능성은 −1이고, 이 결과는 변환이 초평면 반사(hyperplane reflection), (홀수(odd) $n$ 에 대해) 점 반사(point reflection), 또는 또 다른 일종의 부적절한 회전(improper rotation)입니다. 모든 적절한 회전의 행렬은 특수 직교 그룹(special orthogonal group)을 형성합니다.

Two dimensions

이-차원에서, 행렬을 사용하여 회전을 수행하기 위해, 반시계방향으로 회전할 점 $(x, y)$ 은 열 벡터로 작성하고, 그런-다음 각도 $θ$ 에서 계산된 회전 행렬(rotation matrix)을 곱합니다:

{\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}

.

회전 후 점의 좌표는 $x', y'$ 이고, $x'$ 과 $y'$ 에 대해 공식은 다음입니다:

{\begin{aligned}x'&=x\cos \theta -y\sin \theta \\y'&=x\sin \theta +y\cos \theta .\end{aligned}}

벡터 ${\begin{bmatrix}x\\y\end{bmatrix}}$ 와 ${\begin{bmatrix}x'\\y'\end{bmatrix}}$ 는 같은 크기를 가지고 예상된 것처럼 각도 $θ$ 에 의해 분리됩니다.

$R 2$ 평면 위의 점은 역시 복소수(complex number)로 나타낼 수 있습니다: 평면에서 점 $(x, y)$ 는 복소수에 의해 표시됩니다:

z=x+iy

이것은 그것에 $e iθ$ 를 곱하고, 그런-다음 다음과 같이 오일러 공식(Euler's formula)을 사용하여 곱을 확장함으로써 각도 $θ$ 만큼 회전할 수 있습니다:

{\begin{aligned}e^{i\theta }z&=(\cos \theta +i\sin \theta )(x+iy)\\&=x\cos \theta +iy\cos \theta +ix\sin \theta -y\sin \theta \\&=(x\cos \theta -y\sin \theta )+i(x\sin \theta +y\cos \theta )\\&=x'+iy',\end{aligned}}

그리고 실수 부분과 허수 부분을 동일시하면 이-차원 행렬과 같은 결과를 얻을 수 있습니다:

{\begin{aligned}x'&=x\cos \theta -y\sin \theta \\y'&=x\sin \theta +y\cos \theta .\end{aligned}}

복소수는 교환 링(commutative ring)을 형성하기 때문에, 이-차원에서 벡터 회전은 더 높은 차원과 달리 교환적입니다. 그것들은 그러한 회전이 전적으로 회전의 각도에 의해 결정되기 때문에 오직 일 자유도(degree of freedom)를 가집니다.^[3]

Three dimensions

이-차원에서처럼, 행렬은 점 $(x, y, z)$ 을 점 $(x', y', z')$ 으로 회전하기 위해 사용될 수 있습니다. 사용된 행렬은 3×3 행렬이며,

\mathbf {A} ={\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}

이것은 결과를 제공하기 위해 점을 나타내는 벡터에 의해 곱해집니다:

\mathbf {A} {\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}x'\\y'\\z'\end{pmatrix}}

행렬 곱셈(matrix multiplication)의 연산과 함께 모든 적절한 행렬의 집합은 회전 그룹 SO(3)입니다. 행렬 $A$ 는 삼-차원 특수 직교 그룹(special orthogonal group), $SO(3)$ 의 구성원입니다. 즉, 그것은 행렬식(determinant) 1을 갖는 직교 행렬(orthogonal matrix)입니다. 그것이 직교 행렬이라는 것은 그것의 행이 그것의 열과 마찬가지로 직교 단위 벡터(unit vector)의 집합이라는 것을 의미이며 (따라서 그것들은 직교-정규 기저(orthonormal basis)입니다), 행렬이 유효한 회전 행렬인지 발견하고 확인하는 것을 간단하게 만듭니다.

위에-언급된 오일러 각도와 축-각도 표시는 회전 행렬로 쉽게 변환될 수 있습니다.

삼-차원 유클리드 벡터의 회전을 나타내기 위해 또 다른 가능성은 아래에 설명된 쿼터니언입니다.

Quaternions

단위 쿼터니언(quaternion), 또는 버서(versor)는 어떤 면에서 삼-차원 회전의 가장 직관적이지 않은 표시입니다. 그것들은 일반적인 접근 방식의 삼-차원 사례가 아닙니다. 그것들은 행렬보다 간결하고 모든 다른 방법보다 작업하기 쉬우므로, 종종 실제 응용에서 선호됩니다.

버서 (역시 회전 쿼터니언으로 불림)는 넷의 실수로 구성되며, 쿼터니언의 노름(norm)이 1이 되도록 제한됩니다. 이 제약은 필요에 따라 쿼터니언의 자유도를 삼으로 제한합니다. 행렬 및 복소수와 달리, 둘의 곱셈이 필요됩니다:

\mathbf {x'} =\mathbf {qxq} ^{-1},

여기서 $q$ 는 버서, $q -1$ 는 그것의 역(inverse)이고, $x$ 는 영 스칼라 부분(scalar part)을 갖는 쿼터니언으로 취급된 벡터입니다. 쿼터니언은 쿼터니언에 걸쳐 지수 맵(exponential map)에 의해 축 각도 회전의 회전 벡터 형식과 관련될 수 있습니다,

\mathbf {q} =e^{\mathbf {v} /2},

여기서 $v$ 는 쿼터니언으로 취급된 회전 벡터입니다.

왼쪽이든 오른쪽이든 버서에 의한 단일 곱셈은 그 자체로 회전이지만, 사차원에 있습니다. 원점에 대한 임의의 사-차원 회전은 둘의 다른 단위 쿼터니언에 의해, 둘의 쿼터니언 곱셈: 왼쪽에 하나와 오른쪽에 하나로 나타낼 수 있습니다.

Further notes

보다 일반적으로, 임의의 차원에서 좌표 회전은 직교 행렬에 의해 표시됩니다. 행렬 곱셈의 연산과 함께 적절한 회전 (행렬식 = +1)을 설명하는 $n$ 차원에서 모든 직교 행렬의 집합은 특수 직교 그룹(special orthogonal group) $SO(n)$ 을 형성합니다.

행렬은 그것들이 선형 연산자(linear operator)의 직접 표시이기 때문에 특히 많은 숫자의 점이 변환될 때 변환을 수행하는 데 종종 사용됩니다. 다른 방법에서 표현된 회전은 사용되기 전에 종종 행렬로 변환됩니다. 그것들은 동차 좌표(homogeneous coordinates)를 사용하여 회전과 변환을 동시에 나타내기 위해 확장될 수 있습니다. 투영 변환(projective transformation)은 4×4 행렬에 의해 표현됩니다. 그것들이 회전 행렬은 아니지만, 유클리드 회전을 나타내는 변환은 왼쪽 상단 모서리에 3×3 회전 행렬을 가집니다.

행렬의 주요 단점은 그것들이 계산하고 계산을 수행하는 데 더 많은 비용이 든다는 것입니다. 역시 수치적 불안정성(numerical instability)이 우려되는 계산에서 행렬은 이에 더 취약할 수 있으므로, 행렬에 대해 수행하는 데 비용이 많이 드는 직교-정규성(orthonormality)을 복원하는 계산은 더 자주 수행되어야 합니다.

More alternatives to the matrix formalism

위에서 시연했던 것처럼, 셋의 다중-선형 대수 회전 형식주의가 존재합니다: 하나는 이-차원에 대해 U(1), 또는 복소수를 사용하고, 다른 둘은 삼차원과 사차원에 대해 버서, 또는 쿼터니언을 사용합니다.

일반적으로 (심지어 비-유클리드 민코프스키 이차 형식(quadratic form)을 갖춘 벡터에 대해), 벡터 공간의 회전은 이중벡터(bivector)로 표현될 수 있습니다. 이 형식주의는 기하 대수(geometric algebra), 더 일반적으로 리 그룹의 클리퍼드 대수(Clifford algebra) 표시에서 사용됩니다.

양의-한정 유클리드 이차 형식의 경우에서, 등거리변환 그룹 $\mathrm {SO} (n)$ 의 이중 덮는 그룹(covering group)은 스핀 그룹(Spin group), $\mathrm {Spin} (n)$ 으로 알려져 있습니다. 그것은 클리퍼드 대수의 관점에서 편리하게 설명될 수 있습니다. 단위 쿼터니언은 그룹 $\mathrm {Spin} (3)\cong \mathrm {SU} (2)$ 를 제공합니다.

In non-Euclidean geometries

구형 기하학(spherical geometry)에서, $n$ -구 (타원 기하학(elliptic geometry)의 예제)의 직접 운동은 원점 ( $SO(n + 1)$ )에 대한 $(n + 1)$ -차원 유클리드 공간의 회전과 같습니다. 홀수 $n$ 에 대해, 이들 운동의 대부분은 $n$ -구 위에 고정된 점을 가지지 않고, 엄밀히 말하면, 구의 회전이 아닙니다; 그러한 운동은 때때로 클리포드 평행이동으로 참조됩니다. 타원과 쌍곡선(hyperbolic) 기하학에서 고정된 점에 대한 회전은 유클리드 기하학과 다르지 않습니다.

아핀 기하학(Affine geometry)과 투영 기하학(projective geometry)은 구별되는 회전의 개념을 가지지 않습니다.

In relativity

이것의 한 가지 적용은 특수 상대성(special relativity)인데, 왜냐하면 그것은 셋의 공간 차원과 하나의 시간 차원에 의해 확장된 사-차원 공간, 시공간(spacetime)에서 작동하는 것으로 고려될 수 있기 때문입니다. 특수 상대성에서, 이 공간은 선형이고 로렌츠 변환(Lorentz transformation)이라고 불리는 사차원 회전은 실제적인 물리적 해석을 가지고 있습니다. 민코프스키 공간(Minkowski space)은 메트릭 공간(metric space)이 아니고, 용어 등거리변환은 로렌츠 변환에 적용할 수 없습니다.

만약 회전이 오직 셋의 공간 차원에 있으면, 즉 완전히 공간에 있는 평면에서 있으면, 이 회전은 삼차원에서의 공간 회전과 같습니다. 그러나 하나의 공간 차원과 하나의 시간 차원에 의해 확장된 평면에서 회전은 쌍곡선 회전(hyperbolic rotation), 둘의 서로 다른 참조 프레임(reference frames) 사이의 변환이며, 이것은 때때로 "로렌츠 부스트"라고 불립니다. 이들 변환은 민코프스키 공간의 유사-유클리드(pseudo-Euclidean) 본성을 보여줍니다. 그것들은 때때로 스퀴즈 매핑(squeeze mapping)으로 설명되고 평면 도면에서 (1 + 1)-차원 유사-유클리드 기하학을 시각화하는 민코프스키 다이어그램(Minkowski diagram)에 자주 나타납니다. 상대성 이론의 연구는 공간 회전과 쌍곡선 회전에 의해 생성된 로렌츠 그룹(Lorentz group)에 관한 것입니다.^[4]

물리학 및 천문학에서 $SO(3)$ 회전은 유클리드 3-공간에서 2-구체로서의 천구(celestial sphere)의 회전에 해당하는 반면, $SO(3;1) +$ 에서 로렌츠 변환은 천구의 등각(conformal) 변환을 유도합니다. 그것은 뫼비우스 변환(Möbius transformation)으로 알려진 구체 변환의 더 넓은 클래스입니다.

Discrete rotations

Importance

회전은 중요한 대칭(symmetry)의 클래스를 정의합니다: 회전 대칭(rotational symmetry)은 특정 회전에 관해 불변입니다. 원형 대칭(circular symmetry)은 고정된 축에 대한 모든 회전에 관해 불변입니다.

위에서 언급했듯이, 유클리드 회전은 강체 동역학(rigid body dynamics)에 적용됩니다. 게다가, 물리학(physics)에서 수학적 형식주의 (예를 들어 벡터 미적분학(vector calculus))의 대부분은 회전-불변입니다; 더 많은 물리적 측면에 대해 회전(rotation)을 참조하십시오. 위에서 설명된 유클리드 회전과 보다 일반적으로 로렌츠 대칭은 자연의 대칭 법칙으로 생각됩니다. 대조적으로, 반사 대칭(reflectional symmetry)은 자연의 정확한 대칭 법칙이 아닙니다.

Generalizations

실수 직교 행렬과 유사한 복소-값 행렬은 유니태리 행렬(unitary matrices) $\mathrm {U} (n)$ 이며, 이것은 복소 공간에서 회전을 나타냅니다. 주어진 차원 $n$ 에 있는 모든 유니태리 행렬의 집합은 차수 $n$ 의 유니태리 그룹(unitary group) $\mathrm {U} (n)$ 입니다; 그리고 적절한 회전을 나타내는 그것의 부분그룹 (공간의 방향을 유지하는 것)은 차수 $n$ 의 특수 유니태리 그룹(special unitary group) $\mathrm {SU} (n)$ 입니다. 이들 복소 회전은 스피너(spinor)의 문맥에서 중요합니다. $\mathrm {SU} (2)$ 의 원소는 삼-차원 유클리드 회전 (위 참조)과 마찬가지로 스핀(spin)의 각각의 변환을 매개변수화하기 위해 사용됩니다 (SU(2)의 표시 이론을 참조하십시오).

Footnotes

^ Weisstein, Eric W. "Alibi Transformation." From MathWorld--A Wolfram Web Resource.
^ Weisstein, Eric W. "Alias Transformation." From MathWorld--A Wolfram Web Resource.
^ Lounesto 2001, p. 30.
^ Hestenes 1999, pp. 580–588.

References

Hestenes, David (1999). New Foundations for Classical Mechanics. Dordrecht: Kluwer Academic Publishers. ISBN 0-7923-5514-8.

Lounesto, Pertti (2001). Clifford algebras and spinors. Cambridge: Cambridge University Press. ISBN 978-0-521-00551-7.

Brannon, Rebecca M. (2002). "A review of useful theorems involving proper orthogonal matrices referenced to three-dimensional physical space" (PDF). Albuquerque: Sandia National Laboratories.

[1] Weisstein, Eric W. "Alibi Transformation." From MathWorld--A Wolfram Web Resource.

[2] Weisstein, Eric W. "Alias Transformation." From MathWorld--A Wolfram Web Resource.

[3] Lounesto 2001, p. 30.

[4] Hestenes 1999, pp. 580–588.

[1]

[2]

[3]

[4]