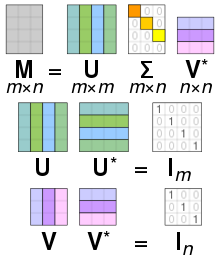
Singular value decomposition

Original article: w:Singular value decomposition

Illustration of the singular value decomposition UΣV^⁎ of a real 2×2 matrix M.

• Top: The action of M, indicated by its effect on the unit disc D and the two canonical unit vectors e₁ and e₂.
• Left: The action of V^⁎, a rotation, on D, e₁, and e₂.
• Bottom: The action of Σ, a scaling by the singular values σ₁ horizontally and σ₂ vertically.
• Right: The action of U, another rotation.

선형 대수(linear algebra)에서, 특이값 분해(singular value decomposition, 줄여서 SVD)는 실수 또는 복소수 행렬의 인수분해입니다. 그것은 직교정규 고유기저를 갖는 정사각 정규 행렬(normal matrix)의 고유분해(eigendecomposition)를 임의의  $m\times n$ 행렬로 일반화합니다. 그것은 극 분해(polar decomposition)와 관련이 있습니다.

구체적으로, $m\times n$ 복소수 행렬 M의 특이값 분해는 $\mathbf {M} =\mathbf {U\Sigma V^{*}}$ 형식의 인수분해이며, 여기서 U는 $m\times m$ 복소 유니태리 행렬(unitary matrix)이고, $\mathbf {\Sigma }$는 대각선 위에 비-음의 실수를 갖는 직사각형 대각 행렬이고, V는 $n\times n$ 복소 유니태리 행렬이고, $\mathbf {V^{*}}$는 V의 켤레 전치(conjugate transpose)입니다. 그러한 분해는 항상 임의의 복소 행렬에 대해 존재합니다. 만약 M이 실수이면, U와 V는 실수 직교(orthogonal) 행렬임을 보장될 수 있습니다; 그러한 맥락에서, SVD는 종종 $\mathbf {U\Sigma V} ^{\mathsf {T}}$로 표시됩니다.

$\mathbf {\Sigma }$의 대각선 엔트리 $\sigma _{i}=\Sigma _{ii}$는 M에 의해 고유하게 결정되고 M의 특이값(singular values)으로 알려져 있습니다. 비-영 특이값의 개수는 M의 랭크(rank)와 같습니다. U의 열과 V의 열은 각각 M의 왼쪽-특이 벡터와 오른쪽-특이 벡터라고 불립니다. 그것들은 직교정규 기저 u₁, ..., u_m 와 v₁, ..., v_n 의 두 집합을 형성하고, 그것들이 값 영을 갖는 특이값 $\sigma _{i}$가 모두 가장 높은-번호 매겨진 열 (또는 행)에 있도록 정렬되면, 특이값 분해는 $\mathbf {M} =\sum _{i=1}^{r}\sigma _{i}\mathbf {u} _{i}\mathbf {v} _{i}^{*}$로 쓸 수 있으며, 여기서 $r\leq \min\{m,n\}$은 M의 랭크입니다.

SVD는 고유하지 않습니다. 특이값 $\Sigma _{ii}$가 내림차순이 되도록 분해를 선택하는 것이 항상 가능합니다. 이 경우에서, $\mathbf {\Sigma }$ (그러나 U와 V는 아님)는 M에 의해 고유하게 결정됩니다.

그 용어는 때때로 컴팩트 SVD(compact SVD), 유사한 분해 $\mathbf {M} =\mathbf {U\Sigma V^{*}}$를 참조하며, 여기서 $\mathbf {\Sigma }$는 크기 $r\times r$의 정사각 대각이며, 여기서 $r\leq \min\{m,n\}$은 M의 랭크이고, 비-영 특이값만 가집니다. 이 변형에서, U는 $m\times r$ 반-유니태리 행렬이고 V는 $n\times r$ 반-유니태리 행렬이며, $\mathbf {U^{*}U} =\mathbf {V^{*}V} =\mathbf {I} _{r}$를 만족합니다.

SVD의 수학적 응용은 유사-역(pseudoinverse) 계산, 행렬 근사화, 및 행렬의 랭크, 치역, 및 널 공간(null space) 결정을 포함합니다. SVD는 역시 신호 처리, 데이터의 최소 제곱 피팅, 및 프로세스 제어와 같은 과학, 공학, 및 통계의 모든 영역에서 매우 유용합니다.

Intuitive interpretations

Animated illustration of the SVD of a 2D, real shearing matrix M. First, we see the unit disc in blue together with the two canonical unit vectors. We then see the actions of M, which distorts the disk to an ellipse. The SVD decomposes M into three simple transformations: an initial rotation V^⁎, a scaling $\mathbf {\Sigma }$ along the coordinate axes, and a final rotation U. The lengths σ₁ and σ₂ of the semi-axes of the ellipse are the singular values of M, namely Σ_1,1 and Σ_2,2.

Visualization of the matrix multiplications in singular value decomposition

Rotation, coordinate scaling, and reflection

M이 m × m 실수 정사각 행렬인 특별한 경우에서, 행렬 U와 V^⁎도 실수 m × m 행렬로 선택될 수 있습니다. 해당 경우에서, "유니태리"는 "직교"와 같습니다. 그런 다음, 여기에 A로 요약된, 대각 행렬과 마찬가지로 단위 행렬을 공간 R^m의 선형 변환(linear transformation) x ↦ Ax로 해석하여, 행렬 U와 V^⁎는 공간의 회전(rotations) 또는 반사(reflection)를 나타내고, 반면에 $\mathbf {\Sigma }$는 각 좌표 x_i를 인수 σ_i만큼 스케일링(scaling)을 나타냅니다. 따라서 SVD 분해는 R^m의 임의의 선형 변환을 세 가지 기하학적 변환: 회전 또는 반사 (V^⁎) 다음에, 좌표별 스케일링 ($\mathbf {\Sigma }$) 다음에, 또 다른 회전 또는 반사 (U)의 합성(composition)으로 분해합니다.

특히, M이 양의 행렬식을 가지면, U와 V^⁎는 반사를 갖는 두 회전, 또는 반사 없이 두 회전으로 선택될 수 있습니다. 만약 행렬식이 음수이면, 그 중 정확히 하나만 반사를 가질 것입니다. 만약 행렬식이 영이면, 각각은 독립적으로 두 유형 중 하나로 선택될 수 있습니다.

만약 행렬 M이 실수이지만 정사각이 아니면, 즉 m ≠ n인 m×n이면, 그것은 Rⁿ에서 R^m으로의 선형 변환으로 해석될 수 있습니다. 그런 다음 U와 V^⁎는 각각 R^m과 Rⁿ의 회전/반사로 선택될 수 있습니다; 그리고 $\mathbf {\Sigma }$는, 첫 번째 $\min\{m,n\}$ 좌표의 스케일링하는 것 외에도, 역시 벡터를 영들로 확장하며, 즉, 후행하는 좌표를 제거하여, Rⁿ을 R^m으로 바꿉니다.

Singular values as semiaxes of an ellipse or ellipsoid

그림에서 볼 수 있듯이, 특이값(singular values)은 2차원에서 타원(ellipse)의 반축의 크기로 해석될 수 있습니다. 이 개념은 n-차원 유클리드 공간(Euclidean space)으로 일반화될 수 있으며, 임의의 n × n 정사각 행렬의 특이값은 n-차원 타원면체(ellipsoid)의 반축의 크기로 고려됩니다. 마찬가지로, 임의의 m × n 행렬의 특이값은 m-차원 공간에서 n-차원 타원면체, 예를 들어 3D 공간에서 (기울어진) 2D 평면에서 타원의 반축의 크기로 볼 수 있습니다. 특이값은 반축의 크기를 인코딩하고, 반면에 특이 벡터는 방향을 인코딩합니다. 자세한 내용에 대해 아래를 참조하십시오.

The columns of U and V are orthonormal bases

U와 V^⁎는 유니태리이기 때문에, 그것들 중 각각의 열은 기저 벡터(basis vectors)로 고려될 수 있는 직교정규 벡터(orthonormal vectors)의 집합을 형성합니다. 행렬 M은 기저 벡터 V_i를 뻗은 단위 벡터 σ_i U_i로 매핑합니다. 유니태리 행렬의 정의에 의해, 켤레 전치 U^⁎와 V에 대해서도 참이며, 단, 뻗음에 따른 특이값의 기하학적 해석이 손실됩니다. 간단히 말해서, U, U^⁎, V와 V^⁎의 열은 직교정규 기저(orthonormal bases)입니다. $\mathbf {M}$이 양수-한정 에르미트 행렬(Hermitian matrix)일 때, U와 V는 모두 $\mathbf {M}$을 대각화하기 위해 사용되는 유니태리 행렬과 같습니다. 어쨌든, $\mathbf {M}$이 양수-한정과 에르미트 행렬이 아니지만 여전히 대각화-가능(diagonalizable)이면, 고유분해(eigendecomposition)와 특이값 분해는 구별됩니다.

Geometric meaning

U와 V는 유니태리이기 때문에, 우리는 U의 열 U₁, ..., U_m은 (이들 공간 위의 표준 스칼라 곱에 관해) K^m의 직교정규 기저를 산출하고 V의 열 V₁, ..., V_n은 Kⁿ의 직교정규 기저를 산출한다는 것을 알고 있습니다.

다음 선형 변환(linear transformation)은

$T\colon \left\{{\begin{aligned}K^{n}&\to K^{m}\\x&\mapsto \mathbf {M} x\end{aligned}}\right.$

이들 직교정규 기저에 관해 특히 간단한 설명을 가집니다: 우리는 다음을 가집니다:

$T(\mathbf {V} _{i})=\sigma _{i}\mathbf {U} _{i},\qquad i=1,\ldots ,\min(m,n),$

여기서 σ_i는 $\mathbf {\Sigma }$의 i-번째 대각 엔트리이고, i > min(m,n)에 대해 T(V_i) = 0입니다.

따라서 SVD 정리의 기하학적 컨텐츠는 다음과 같이 요약될 수 있습니다: 모든 각 선형 맵 T : Kⁿ → K^m에 대해, T가 Kⁿ의 i-번째 기저 벡터를 K^m의 i-번째 기저 벡터의 비-음의 배수로 매핑하고, 나머지 기저 벡터를 영으로 보냄을 만족하는 Kⁿ과 K^m의 직교정규 기저를 찾을 수 있습니다. 이들 기저에 관해, 따라서 맵 T는 비-음의 실수 대각선 엔트리를 갖는 대각 행렬로 표시됩니다.

적어도 실수 벡터 공간에서 연구할 때, 특이값과 SVD 인수분해에 대해 좀 더 시각적인 느낌을 얻기 위해, Rⁿ에서 반지름 1의 구 S를 생각해 보십시오. 선형 맵 T는 이 구를 R^m에서 타원면체(ellipsoid)에 매핑합니다. 비-영 특이값은 단순히 이 타원면체의 반축의 길이입니다. 특히 n = m이고 모든 특이값이 구별되고 비-영이면, 선형 맵 T의 SVD는 세 개의 연이은 이동의 연속으로 쉽게 분석될 수 있습니다: 타원면체 T(S)와 특히 그것의 축을 생각해 보십시오; 그런-다음 T에 의해 이들 축 위로 보내진 Rⁿ에서 방향을 생각해 보십시오. 이들 방향은 서로 직교합니다. 먼저 이들 방향을 Rⁿ의 좌표축으로 보내는 등거리변환 V^⁎를 적용합니다. 두 번째 이동에서, T(S)의 반축 길이를 잡아 늘리는 계수로 사용하여 좌표축을 따라 대각선화되고 각 방향에서 늘어나거나 줄어드는 자기사상(endomorphism) D를 적용합니다. 합성 D ∘ V^⁎는 그런-다음 단위 구를 T(S)에 등거리-변환적인 타원면체 위로 보냅니다. 세 번째이자 마지막 이동을 정의하기 위해, 이 타원면체에 등거리변환 U를 T(S)를 얻기 위해 적용합니다. 쉽게 확인할 수 있듯이, 합성 U ∘ D ∘ V^⁎는 T와 일치합니다.

Example

다음 4 × 5 행렬을 생각해 보십시오:

$\mathbf {M} ={\begin{bmatrix}1&0&0&0&2\\0&0&3&0&0\\0&0&0&0&0\\0&2&0&0&0\end{bmatrix}}$

이 행렬의 특이값 분해는 UΣV^⁎에 의해 제공됩니다:

${\begin{aligned}\mathbf {U} &={\begin{bmatrix}\color {Green}0&\color {Blue}-1&\color {Cyan}0&\color {Emerald}0\\\color {Green}-1&\color {Blue}0&\color {Cyan}0&\color {Emerald}0\\\color {Green}0&\color {Blue}0&\color {Cyan}0&\color {Emerald}-1\\\color {Green}0&\color {Blue}0&\color {Cyan}-1&\color {Emerald}0\end{bmatrix}}\\[6pt]{\boldsymbol {\Sigma }}&={\begin{bmatrix}3&0&0&0&\color {Gray}{\mathit {0}}\\0&{\sqrt {5}}&0&0&\color {Gray}{\mathit {0}}\\0&0&2&0&\color {Gray}{\mathit {0}}\\0&0&0&\color {Red}\mathbf {0} &\color {Gray}{\mathit {0}}\end{bmatrix}}\\[6pt]\mathbf {V} ^{*}&={\begin{bmatrix}\color {Violet}0&\color {Violet}0&\color {Violet}-1&\color {Violet}0&\color {Violet}0\\\color {Plum}-{\sqrt {0.2}}&\color {Plum}0&\color {Plum}0&\color {Plum}0&\color {Plum}-{\sqrt {0.8}}\\\color {Magenta}0&\color {Magenta}-1&\color {Magenta}0&\color {Magenta}0&\color {Magenta}0\\\color {Orchid}0&\color {Orchid}0&\color {Orchid}0&\color {Orchid}1&\color {Orchid}0\\\color {Purple}-{\sqrt {0.8}}&\color {Purple}0&\color {Purple}0&\color {Purple}0&\color {Purple}{\sqrt {0.2}}\end{bmatrix}}\end{aligned}}$

스케일링 행렬 $\mathbf {\Sigma }$는 대각선 밖의 (회색 기울임꼴) 영이고 하나의 대각선 원소는 영 (빨간색 굵은 글씨, 어두운 모드에서 밝은 파란색 굵은 글씨)입니다. 게다가, 행렬 U와 V^⁎는 유니태리(unitary)이기 때문에, 각각의 켤레 전치를 곱하면 아래와 같이 항등 행렬(identity matrices)을 산출합니다. 이 경우에서, U와 V^⁎는 실수 값이기 때문에, 각각은 직교 행렬(orthogonal matrix)입니다.

${\begin{aligned}\mathbf {U} \mathbf {U} ^{*}&={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}=\mathbf {I} _{4}\\[6pt]\mathbf {V} \mathbf {V} ^{*}&={\begin{bmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\end{bmatrix}}=\mathbf {I} _{5}\end{aligned}}$

이 특정 특이값 분해는 고유하지 않습니다. 다음이 역시 유효한 특이값 분해임을 만족하는 $\mathbf {V}$를 선택하십시오:

$\mathbf {V} ^{*}={\begin{bmatrix}\color {Violet}0&\color {Violet}1&\color {Violet}0&\color {Violet}0&\color {Violet}0\\\color {Plum}0&\color {Plum}0&\color {Plum}1&\color {Plum}0&\color {Plum}0\\\color {Magenta}{\sqrt {0.2}}&\color {Magenta}0&\color {Magenta}0&\color {Magenta}0&\color {Magenta}{\sqrt {0.8}}\\\color {Orchid}{\sqrt {0.4}}&\color {Orchid}0&\color {Orchid}0&\color {Orchid}{\sqrt {0.5}}&\color {Orchid}-{\sqrt {0.1}}\\\color {Purple}-{\sqrt {0.4}}&\color {Purple}0&\color {Purple}0&\color {Purple}{\sqrt {0.5}}&\color {Purple}{\sqrt {0.1}}\end{bmatrix}}$

SVD and spectral decomposition

Singular values, singular vectors, and their relation to the SVD

비-음의 실수 σ가 M에 대해 특이값(singular value)인 것과 다음임을 만족하는 K^m에 단위-길이 벡터 $\mathbf {u}$와 Kⁿ에 $\mathbf {v}$가 존재하는 것은 필요충분 조건입니다:

$\mathbf {Mv} =\sigma \mathbf {u} \,{\text{ and }}\mathbf {M} ^{*}\mathbf {u} =\sigma \mathbf {v} .$

벡터 $\mathbf {u}$와 $\mathbf {v}$는 각각 σ에 대해 왼쪽-특이 벡터(left-singular vectors) 및 오른쪽-특이 벡터(right-singular vectors)라고 불립니다.

임의의 특이값 분해에서

$\mathbf {M} =\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}$

$\mathbf {\Sigma }$의 대각선 엔트리는 M의 특이값과 같습니다. U와 V의 첫 번째 p = min(m, n) 열은, 각각, 해당 특이값에 대한 왼쪽- 및 오른쪽-특이 벡터입니다. 결과적으로, 위의 정리는 다음을 의미합니다:

• m × n 행렬 M은 많아야 p 구별되는 특이값을 가집니다.
• M의 각 특이값의 왼쪽-특이 벡터를 스팬하는 기저 벡터의 부분집합을 갖는 K^m에 대해 유니태리 기저(unitary basis) U를 찾는 것이 항상 가능합니다.
• M의 각 특이값의 오른쪽-특이 벡터를 스팬하는 기저 벡터의 부분집합을 갖는 Kⁿ에 대해 유니태리 기저(unitary basis) V를 찾는 것이 항상 가능합니다.

선형적으로 독립인 두 개의 왼쪽 (또는 오른쪽) 특이 벡터를 찾을 수 있는 특이값은 퇴화(degenerate)라고 불립니다. 만약 $\mathbf {u} _{1}$과 $\mathbf {u} _{2}$가 둘 다 특이값 σ에 해당하는 두 개의 왼쪽-특이 벡터이면, 두 벡터의 임의의 정규화된 선형 조합은 특이값 σ에 해당하는 왼쪽-특이 벡터이기도 합니다. 유사한 설명은 오른쪽-특이 벡터에 대해 참입니다. 독립적인 왼쪽 및 오른쪽-특이 벡터의 개수가 일치하고, 이들 특이 벡터는 모두 같은 값 σ를 갖는 $\mathbf {\Sigma }$의 대각선 원소에 해당하는 U와 V의 같은 열에 나타납니다.

하나의 예외로서, 특이값 0의 왼쪽 및 오른쪽-특이 벡터는 각각 M의 여-커널(cokernel)과 커널(kernel)에 있는 모든 단위 벡터를 구성하며, 이는 랭크-널러티 정리(rank–nullity theorem)에 의해 m ≠ n이면 같은 차원이 될 수 없습니다. 심지어 모든 특이값이 비-영이더라도, m > n이면 여커널은 비-자명하며, 이 경우에서 U는 여커널에서 m − n 직교 벡터로 채워집니다. 반대로, m < n이면, V는 커널에서 n − m 직교 벡터로 채워집니다. 어쨌든, 0의 특이값이 존재하면, U 또는 V의 여분의 열은 이미 왼쪽 또는 오른쪽-특이 벡터로 나타납니다.

비-퇴화 특이값은 단위-위상 인수 e^iφ에 의한 곱셈까지 (실수 경우에 대해 부호까지) 고유한 왼쪽- 및 오른쪽-특이 벡터를 항상 가집니다. 결과적으로, 정사각 행렬 M의 모든 특이값이 비-퇴화이고 비-영이면, 특이값 분해는 단위-위상 인수에 의한 U의 열의 곱셈과 동시에 같은 단위-위상 인수에 의한 V의 해당하는 열의 곱셈까지 고유합니다. 일반적으로, SVD는 각 특이값의 부분공간을 스팬하는 U와 V 둘 다의 열 벡터에 균등하게 적용되는 임의적인 유니태리 변환까지, 그리고 각각 M의 커널과 여-커널을 스팬하는 U와 V의 벡터 위에 임의적인 유니태리 변환까지 고유합니다.

Relation to eigenvalue decomposition

특이값 분해는 임의의 m × n 행렬에 적용될 수 있다는 의미에서 매우 일반적이지만, 고윳값 분해(eigenvalue decomposition)는 제곱된 대각화-가능 행렬(diagonalizable matrices)에만 적용될 수 있습니다. 그럼에도 불구하고, 두 분해는 서로 관련되어 있습니다.

만약 M이 SVD $\mathbf {M} =\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}$를 가지면, 다음 두 관계는 유지됩니다:

${\begin{aligned}\mathbf {M} ^{*}\mathbf {M} &=\mathbf {V} {\boldsymbol {\Sigma }}^{*}\mathbf {U} ^{*}\,\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}=\mathbf {V} ({\boldsymbol {\Sigma }}^{*}{\boldsymbol {\Sigma }})\mathbf {V} ^{*}\\\mathbf {M} \mathbf {M} ^{*}&=\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}\,\mathbf {V} {\boldsymbol {\Sigma }}^{*}\mathbf {U} ^{*}=\mathbf {U} ({\boldsymbol {\Sigma }}{\boldsymbol {\Sigma }}^{*})\mathbf {U} ^{*}\end{aligned}}$

이들 관계의 오른쪽 변은 왼쪽 변의 고윳값 분해를 나타냅니다. 결과로써:

• V의 열 (오른쪽-특이 벡터라고 참조됨)은 M^⁎M이 고유벡터(eigenvectors)입니다.
• U의 열 (왼쪽-특이 벡터라고 참조됨)은 MM^⁎의 고유벡터입니다.
• $\mathbf {\Sigma }$의 비-영 원소 (비-영 특이값)는 M^⁎M 또는 MM^⁎의 비-영 고윳값(eigenvalues)의 제곱근입니다.

M이 정규 행렬(normal matrix)이고, 따라서 역시 제곱된 것인 특수한 경우에서, 스펙트럼 정리(spectral theorem)는 고유벡터의 기저를 사용하여 유니태리적으로 대각화될 수 있고, 따라서 대각선을 따라 복소수 요소 σ_i를 갖는 일부 유니태리 행렬 U와 대각 행렬 D에 대해 $\mathbf {M} =\mathbf {U} \mathbf {D} \mathbf {U} ^{*}$로 분해될 수 있음을 보증합니다. M이 양수 반-한정(positive semi-definite)일 때, σ_i는 분해 M = UDU^⁎이 역시 특이값 분해가 되도록 비-음의 실수일 것입니다. 그렇지 않으면, 그것은 각 σ_i의 위상 e^iφ를 해당하는 V_i 또는 U_i로 이동함으로써 SVD로 다시 캐스팅될 수 있습니다. SVD를 비-정규 행렬로의 자연스러운 연결은 극 분해(polar decomposition) 정리: M = SR를 통해 이루어지며, 여기서 S = UΣU^⁎는 양수 반한정 및 정규이고, R = UV^⁎는 유니태리입니다.

따라서, 양수 반-한정 행렬을 제외하고, M의 고윳값 분해와 SVD는 관련되어 있지만 다릅니다: 고윳값 분해는 M = UDU⁻¹이며, 여기서 U는 반드시 유니태리일 필요는 없고 D는 반드시 양수 반-한정일 필요는 없고, 반면에 SVD는 M = UΣV^⁎이며, 여기서 $\mathbf {\Sigma }$는 대각이고 양수 반한정이고, U와 V는 행렬 M을 통하지 않고는 반드시 관련이 없는 유니태리 행렬입니다. 결함-없는 정사각 행렬만 고윳값 분해를 가지지만, 임의의 $m\times n$ 행렬은 SVD를 가집니다.

Applications of the SVD

Pseudoinverse

특이값 분해는 행렬의 유사역(pseudoinverse)을 계산하기 위해 사용될 수 있습니다. (다양한 저자는 유사역에 대해 서로 다른 표기법을 사용합니다; 여기서는 ^†를 사용합니다.) 실제로, 특이값 분해 M = UΣV^⁎를 갖는 행렬 M의 유사역은 다음입니다:

M^† = V Σ^† U^⁎

여기서 Σ^†은 Σ의 유사역이며, 이는 모든 각 비-영 대각 엔트리를 역수(reciprocal)로 대체하고 결과 행렬을 전치함으로써 형성됩니다. 유사역은 선형 최소 제곱(linear least squares) 문제를 해결하기 위한 한 가지 방법입니다.

Solving homogeneous linear equations

동차 선형 방정식(homogeneous linear equations)의 집합은 행렬 A와 벡터 x에 대해 Ax = 0으로 쓸 수 있습니다. 전형적인 상황은 A가 알려져 있고 비-영 x가 방정식을 만족시키는 결정되어야 하는 것입니다. 그러한 x는 A의 널 공간(null space)에 속하고 때때로 A의 (오른쪽) 널 벡터라고도 불립니다. 벡터 x는 영(zero)인 A의 특이값에 해당하는 오른쪽-특이 벡터로 특성화될 수 있습니다. 이 관찰은 A가 정사각 행렬이고 사라지는 특이값을 가지지 않으면, 그 방정식은 비-영 x를 해로 가지지 않는다는 것을 의미합니다. 그,것은 역시 여러 개의 사라지는 특이값이 있으면, 해당 오른쪽-특이 벡터의 임의의 선형 조합이 유효한 해임을 의미합니다. (오른쪽) 널 벡터의 정의와 유사하게, x^⁎A = 0를 만족시키는 비-영 x가, x^⁎가 x의 켤레 전치를 나타내는 것과 함께, A의 왼쪽 널 벡터라고 불립니다.

Total least squares minimization

전체 최소 제곱(total least squares) 문제는 ||x|| = 1 제약 조건 아래에서 벡터 Ax의 2-노름(2-norm)을 최소화하는 벡터 x를 찾습니다. 해는 가장 작은 특이값에 해당하는 A의 오른쪽-특이 벡터로 밝혀졌습니다.

Range, null space and rank

SVD의 또 다른 응용은 행렬 M의 치역(range)과 널 공간(null space)을 명시적 표현을 제공한다는 것입니다. M의 사라지는 특이값에 해당하는 오른쪽-특이 벡터는 M의 널 공간을 스팬하고 왼쪽-특이 벡터는 M의 비-영 특이값에 해당하는 왼쪽-특이 벡터는 M의 치역을 스팬합니다. 예를 들어, 위의 예제에서 널 공간은 V^⁎의 마지막 두 행에 의해 스팬되고 치역은 U의 처음 3개 열에 의해 스팬됩니다.

결과로써, M의 랭크(rank)는 $\mathbf {\Sigma }$에서 비-영 대각선 원소의 개수와 같은 비-영 특이값의 개수와 같습니다. 수치 선형 대수에서 특이값은 행렬의 유효한 랭크(effective rank)를 결정하기 위해 사용될 수 있는데, 왜냐하면 반올림 오차(rounding error)는 랭크가 부족한 행렬에서 작지만 비-영 특이값으로 이어질 수 있기 때문입니다. 상당한 간격을 넘어서는 특이값은 수치적으로 영과 동등하다고 가정됩니다.

Low-rank matrix approximation

일부 실제 응용에서는 행렬 M을 특정 랭크 r을 가지는 잘린 또 다른 행렬 ${\tilde {\mathbf {M} }}$으로 근사하는 문제를 해결해야 합니다. 근사가 $\operatorname {rank} \left({\tilde {\mathbf {M} }}\right)=r$이라는 제약 조건 아래에서 M과 ${\tilde {\mathbf {M} }}$ 사이의 차이의 프로베니우스 노름(Frobenius norm)을 최소화하는 것에 기초한 경우에서, 해는 M의 SVD, 즉, 다음에 의해 제공된다는 것이 밝혀졌습니다:

${\tilde {\mathbf {M} }}=\mathbf {U} {\tilde {\boldsymbol {\Sigma }}}\mathbf {V} ^{*},$

여기서 ${\tilde {\boldsymbol {\Sigma }}}$는 r개의 가장 큰 특이값만 포함한다는 점을 제외하면 $\mathbf {\Sigma }$와 같은 행렬입니다 (다른 특이값은 영에 의해 대체됩니다). 이것은 에카르트-영 정리(Eckart–Young theorem)로 알려져 있는데, 왜냐하면 그것은 1936년에 그들 두 저자에 의해 증명되었기 때문입니다 (비록 나중에 이전 저자에게도 알려진 것으로 밝혀졌지만; Stewart 1993 참조).

Separable models

SVD는 행렬을 분리-가능한 행렬의 가중된, 순서화된 합으로 분해하는 것으로 생각될 수 있습니다. 분리-가능에 의해, 행렬 A가 두 벡터 A = u ⊗ v, 또는, 좌표에서, $A_{ij}=u_{i}v_{j}$의 밖의 곱(outer product)으로 쓸 수 있음을 의미합니다. 구체적으로, 행렬 M은 다음으로 분해될 수 있습니다:

$\mathbf {M} =\sum _{i}\mathbf {A} _{i}=\sum _{i}\sigma _{i}\mathbf {U} _{i}\otimes \mathbf {V} _{i}.$

여기서 U_i와 V_i는 해당 SVD 행렬의 i-번째 열이고, σ_i는 순서화된 특이값이고, 각 A_i는 분리-가능합니다. SVD는 이미지 처리 필터를 분리-가능한 수평 및 수직 필터로 분해를 찾기 위해 사용될 수 있습니다. 비-영 σ_i의 개수는 정확히 행렬의 랭크라는 점에 주목하십시오.

분리-가능 모델은 종종 생물학적 시스템에서 발생하고, SVD 인수분해는 그러한 시스템을 분석하는 데 유용합니다. 예를 들어, 일부 시각적 영역 V1 단순 세포의 수용 필드는 공간 영역에서 가보르 필터(Gabor filter)에 시간 영역에서 변조 함수를 곱하여 잘 설명될 수 있습니다. 따라서, 예를 들어, 역 상관(reverse correlation)을 통해 평가된 선형 필터가 주어지면, 두 공간 차원을 하나의 차원으로 재배열하여, SVD를 통해 분해될 수 있는 2-차원 필터 (공간, 시간)를 산출할 수 있습니다. SVD 인수분해에서 U의 첫 번째 열은 가보르이고 반면에 V의 첫 번째 열은 시간 변조를 나타냅니다 (또는 그 반대). 그런-다음 분리성 지수를 정의할 수 있습니다:

$\alpha ={\frac {\sigma _{1}^{2}}{\sum _{i}\sigma _{i}^{2}}},$

이는 분해에서 첫 번째 분리-가능 행렬에 의해 설명되는 행렬 M에서 거듭제곱의 비율(fraction)입니다.

Nearest orthogonal matrix

정사각 행렬 A의 SVD를 사용하여 A에 가장 가까운 직교 행렬(orthogonal matrix) O를 결정할 수 있습니다. 적합도는 O − A의 프로베니우스 노름(Frobenius norm)으로 측정됩니다. 그 해는 곱 UV^⁎입니다. 직교 행렬은 A = UΣV^⁎이면 곱 A = UV^⁎는 특이값을 1로 바꾸는 총양이 되도록 분해 UIV^⁎를 가지기 때문에 이는 직관적으로 의미가 있으며, 여기서 I는 항등 행렬입니다. 동등하게, 그 해는 위에 설명된 대로 늘림 및 회전의 순서로 극 분해 M = RP = P'R의 유니태리 행렬 R = UV^⁎입니다.

모양 분석(shape analysis)에 흥미로운 적용이 가능한 유사한 문제는 직교 프로크루스테스 문제(orthogonal Procrustes problem)이며, 이는 A를 B에 가장 가깝게 매핑하는 직교 행렬 O를 찾는 것으로 구성됩니다. 구체적으로,

$\mathbf {O} ={\underset {\Omega }{\operatorname {argmin} }}\|\mathbf {A} {\boldsymbol {\Omega }}-\mathbf {B} \|_{F}\quad {\text{subject to}}\quad {\boldsymbol {\Omega }}^{\textsf {T}}{\boldsymbol {\Omega }}=\mathbf {I} ,$

여기서 $\|\cdot \|_{F}$는 프로베니우스 노름을 나타냅니다.

이 문제는 주어진 행렬 M = A^TB에 가장 가까운 직교 행렬을 찾는 것과 동등합니다.

The Kabsch algorithm

캅슈 알고리듬(Kabsch algorithm, 다른 분야에서는 와바의 문제(Wahba's problem)라고 함)은 SVD를 대응하는 점 집합을 갖는 점 집합과 정렬하는 (최소-제곱 최소화에 관해) 최적의 회전을 계산하기 위해 사용합니다. 그것은 다른 응용 분야 중에서도 분자 구조를 비교하기 위해 사용됩니다.

Signal processing

SVD 및 유사역은 신호 처리(signal processing), 이미지 처리(image processing), 및 빅 데이터 (예를 들어, 게놈 신호 처리)에 성공적으로 적용되어 왔습니다.

Astrodynamics

천체동역학(Astrodynamics)에서, SVD와 그 변형은 전달 궤적 설계 및 궤도 관측소-유지(Orbital station-keeping)에 적합한 기동 방향을 결정하는 옵션으로 사용됩니다.

Other examples

SVD는 역시 선형 역 문제(inverse problems)의 연구에 광범위하게 적용되고 티크호노프(Tikhonov)의 방법과 같은 정규화 방법의 분석에 유용합니다. 그것은 주요 성분 분석(principal component analysis)과 대응 분석(correspondence analysis), 및 신호 처리(signal processing)와 패턴 인식(pattern recognition)과 관련된 통계학에서 널리 사용됩니다. 그것은 역시 비-스케일된 모드 모양(mode shapes)이 특이 벡터로부터 결정될 수 있는 출력-전용 양상 해석(modal analysis)에 사용됩니다. 또 다른 용도는 자연-언어 텍스트 처리에서 잠재 의미론적 인덱싱(latent semantic indexing)입니다.

선형 또는 선형화된 시스템과 관련된 일반적인 수치 계산에서, 문제의 규칙성 또는 특이성을 특성화하는 보편 상수가 있으며, 이는 시스템의 "조건 개수" $\kappa :=\sigma _{\text{max}}/\sigma _{\text{min}}$입니다. 그것은 종종 그러한 시스템에서 주어진 계산 스킴의 오류율이나 수렴률을 제어합니다.

SVD는 역시 슈미트 분해(Schmidt decomposition)라고 참조되는 형식으로 양자 정보(quantum information)의 분야에서 결정적 역할을 합니다. 그것을 통해, 두 양자 시스템의 상태가 자연스럽게 분해되어, 두 시스템이 얽히기 위한 필요충분 조건($\mathbf {\Sigma }$ 행렬의 랭크가 1보다 크면)을 제공합니다.

다소 큰 행렬에 대한 SVD의 적용 중 하나는 수치 날씨 예측(numerical weather prediction)에 있으며, 여기서 랭크쏘스 방법(Lanczos methods)은 주어진 초기 전방 시간 구간 동안 중앙 수치 날씨 예측에 대한 가장 선형적으로 빠르게 성장하는 소수의 섭동을 추정하기 위해 사용됩니다; 즉, 해당 시간 구간에 걸쳐 지구 날씨에 대한 선형화된 전파자의 가장 큰 특이값에 해당하는 특이 벡터입니다. 이 경우에서 출력 특이 벡터는 전체 날씨 시스템입니다. 그런 다음 이들 섭동은 전체 비선형 모델을 통해 실행되어 앙상블 예측(ensemble forecast)을 생성하며, 현재 중앙 예측 주변에 대해 허용되어야 하는 일부 불확실성에 대한 처리를 제공합니다.

SVD는 역시 축소된 차수 모델링에 적용되어 왔습니다. 축소된 차수 모델링의 목적은 모델링될 복잡한 시스템에서 자유도의 개수를 줄이는 것입니다. SVD는 방사형 기저 함수(radial basis functions)와 결합되어 3-차원 비정상 흐름 문제에 대한 해를 보간했습니다.

흥미롭게도, SVD는 지상-기반 중력-파동 간섭계 aLIGO에 의한 중력 파동형식 모델링을 개선하기 위해 사용되어 왔습니다. SVD는 중력-파동 검색을 지원하고 두 가지 다른 파동형식 모델을 업데이트하기 위해 파동형식 생성의 정확성과 속도를 높이는 데 도움이 될 수 있습니다.

특이값 분해는 추천 시스템(recommender systems)에서 사람들의 항목 평가를 예측하기 위해 사용됩니다. 분산 알고리듬은 상용 기계의 클러스터에서 SVD를 계산하는 목적에 대해 개발되어 왔습니다.

낮은-랭크 SVD는 질병 발생 탐지에 응용을 갖는 시공간 데이터로부터 핫스팟 탐지를 위해 적용되어 왔습니다. SVD와 고차 SVD의 조합은 질병 감시(disease surveillance)에서 복잡한 데이터 스트림 (공간과 시간 차원을 갖는 다변수 데이터)의 실시간 사건 감지에도 적용되어 왔습니다.

Proof of existence

행렬 M의 고윳값 λ는 대수적 관계 Mu = λu로 특징지어집니다. M이 에르미트(Hermitian)일 때, 변형 특성화도 사용할 수 있습니다. M을 실수 n × n 대칭 행렬이라고 놓습니다. 다음을 정의합니다:

${\begin{cases}f:\mathbb {R} ^{n}\to \mathbb {R} \\f:\mathbf {x} \mapsto \mathbf {x} ^{\textsf {T}}\mathbf {M} \mathbf {x} \end{cases}}$

극단 값 정리(extreme value theorem)에 의해, 이 연속 함수는 단위 구 {||x|| = 1}로 제한될 때 일부 u에서 최댓값에 도달합니다. 라그랑주 곱셈수(Lagrange multipliers) 정리에 의해, u는 반드시 일부 실수 λ에 대해 다음을 만족시킵니다:

$\nabla \mathbf {u} ^{\textsf {T}}\mathbf {M} \mathbf {u} -\lambda \cdot \nabla \mathbf {u} ^{\textsf {T}}\mathbf {u} =0$

나블라 기호, ∇는 델(del) 연산자 (x에 관한 미분)입니다. M의 대칭성을 사용하여, 우리는 다음을 얻습니다:

$\nabla \mathbf {x} ^{\textsf {T}}\mathbf {M} \mathbf {x} -\lambda \cdot \nabla \mathbf {x} ^{\textsf {T}}\mathbf {x} =2(\mathbf {M} -\lambda \mathbf {I} )\mathbf {x} .$

그러므로 Mu = λu이므로, u는 M의 단위 길이 고유벡터입니다. M의 모든 각 단위 길이 고유벡터 v에 대해, 그것의 고윳값은 f(v)이므로, λ는 M의 가장 큰 고윳값입니다. u의 직교 여 위에 수행된 같은 계산은 다음으로 가장 큰 고윳값을 제공하고 이런 식으로 계속됩니다. 복소 에르미트 사례도 비슷합니다; 그곳에서 f(x) = x* M x는 2n개의 실수 변수의 실수-값 함수입니다.

특이값은 그것들이 대수적으로 또는 변동 원리로 설명될 수 있다는 점에서 유사합니다. 고윳값의 경우와 달리, M의 에르미트성 또는 대칭성은 더 이상 필요하지 않습니다.

이 섹션은 특이값 분해의 존재에 대한 이들 두 가지 주장을 제시합니다.

Based on the spectral theorem

$\mathbf {M}$을 m × n 복소수 행렬이라고 놓습니다. $\mathbf {M} ^{*}\mathbf {M}$은 양수 반-한정이고 에르미트이므로, 스펙트럼 정리(spectral theorem)에 의해, 다음임을 만족하는 n × n 유니태리 행렬 $\mathbf {V}$가 존재합니다:

$\mathbf {V} ^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} ={\bar {\mathbf {D} }}={\begin{bmatrix}\mathbf {D} &0\\0&0\end{bmatrix}},$

여기서 $\mathbf {D}$는 차원 $\ell \times \ell$의 대각이고 양수 한정이며, $\ell$는 $\mathbf {M} ^{*}\mathbf {M}$의 비-영 고윳값의 개수입니다 (이는 $\ell \leq \min(n,m)$을 확인하기 위해 표시될 수 있습니다). $\mathbf {V}$는 여기서 정의에 의해 $i$-번째 열이 고윳값 ${\bar {\mathbf {D} }}_{ii}$에 해당하는 ${\bar {\mathbf {D} }}_{ii}$의 $i$-번째 고유벡터인 행렬임에 주목하십시오. 더욱이, $j>\ell$에 대해 $\mathbf {V}$의 $j$-번째 열은 고윳값 ${\bar {\mathbf {D} }}_{jj}=0$을 갖는 $\mathbf {M} ^{*}\mathbf {M}$의 고유벡터입니다. 이것은 $\mathbf {V}$를 $\mathbf {V} ={\begin{bmatrix}\mathbf {V} _{1}&\mathbf {V} _{2}\end{bmatrix}}$로 씀으로써 표현될 수 있으며, 여기서 $\mathbf {V} _{1}$과 $\mathbf {V} _{2}$의 열은 각각 비-영 고윳값과 영 고윳값에 해당하는 $\mathbf {M} ^{*}\mathbf {M}$의 고유벡터를 포함합니다. 이것을 사용하여 $\mathbf {V}$를 다시 작성하면, 방정식은 다음이 됩니다:

${\begin{bmatrix}\mathbf {V} _{1}^{*}\\\mathbf {V} _{2}^{*}\end{bmatrix}}\mathbf {M} ^{*}\mathbf {M} {\begin{bmatrix}\mathbf {V} _{1}&\mathbf {V} _{2}\end{bmatrix}}={\begin{bmatrix}\mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}&\mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{2}\\\mathbf {V} _{2}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}&\mathbf {V} _{2}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{2}\end{bmatrix}}={\begin{bmatrix}\mathbf {D} &0\\0&0\end{bmatrix}}.$

이것은 다음임을 의미합니다:

$\mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}=\mathbf {D} ,\quad \mathbf {V} _{2}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{2}=\mathbf {0} .$

더욱이, 두 번째 방정식은 $\mathbf {M} \mathbf {V} _{2}=\mathbf {0}$를 의미합니다. 마지막으로, $\mathbf {V}$의 유니태리-성은, $\mathbf {V} _{1}$과 $\mathbf {V} _{2}$의 관점에서, 다음 조건으로 변환됩니다:

${\begin{aligned}\mathbf {V} _{1}^{*}\mathbf {V} _{1}&=\mathbf {I} _{1},\\\mathbf {V} _{2}^{*}\mathbf {V} _{2}&=\mathbf {I} _{2},\\\mathbf {V} _{1}\mathbf {V} _{1}^{*}+\mathbf {V} _{2}\mathbf {V} _{2}^{*}&=\mathbf {I} _{12},\end{aligned}}$

여기서 항등 행렬에 대한 아래첨자는 그것들이 서로 다른 차원임을 표시하기 위해 사용됩니다.

이제 다음을 정의해 보십시오:

$\mathbf {U} _{1}=\mathbf {M} \mathbf {V} _{1}\mathbf {D} ^{-{\frac {1}{2}}}.$

그런-다음,

$\mathbf {U} _{1}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}=\mathbf {M} \mathbf {V} _{1}\mathbf {D} ^{-{\frac {1}{2}}}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}=\mathbf {M} (\mathbf {I} -\mathbf {V} _{2}\mathbf {V} _{2}^{*})=\mathbf {M} -(\mathbf {M} \mathbf {V} _{2})\mathbf {V} _{2}^{*}=\mathbf {M} ,$

왜냐하면 $\mathbf {M} \mathbf {V} _{2}=\mathbf {0}$이기 때문입니다. 이것은 $\mathbf {M} \mathbf {V} _{1}\mathbf {V} _{1}^{*}=\mathbf {M}$이라는 사실의 즉각적인 결과로도 볼 수 있습니다. 이것은 $\{{\boldsymbol {v}}_{i}\}_{i=1}^{\ell }$가 비-사라지는 고윳값 $\{\lambda _{i}\}_{i=1}^{\ell }$에 대응하는 $\mathbf {M} ^{*}\mathbf {M}$의 고유벡터의 집합이면, $\{\mathbf {M} {\boldsymbol {v}}_{i}\}_{i=1}^{\ell }$는 직교 벡터의 집합이고, $\{\lambda _{i}^{-1/2}\mathbf {M} {\boldsymbol {v}}_{i}\}_{i=1}^{\ell }$는 (일반적으로 완전하지 않은) 직교정규 벡터의 집합이라는 관찰과 동등합니다. 이것은 위에서 사용된 행렬 형식 $\mathbf {V} _{1}$은 그 열이 $\{{\boldsymbol {v}}_{i}\}_{i=1}^{\ell }$인 행렬, $\mathbf {V} _{2}$는 그 열이 사라지는 고윳값을 갖는 $\mathbf {M} ^{*}\mathbf {M}$의 고유벡터인 행렬, 및 $\mathbf {U} _{1}$은 그 열이 벡터 $\{\lambda _{i}^{-1/2}\mathbf {M} {\boldsymbol {v}}_{i}\}_{i=1}^{\ell }$인 행렬을 나타내는 것과 일치합니다.

우리는 이것이 $\mathbf {U} _{1}$과 $\mathbf {V} _{1}$이, 그것들이 정사각이 아닐 수 있기 때문에, 일반적으로 유니태리가 아니라는 점을 제외하면 거의 원하는 결과라는 것을 알 수 있습니다. 어쨌든, 우리는 $\mathbf {D}$의 차원이 $m$과 $n$보다 크지 않기 때문에 $\mathbf {U} _{1}$의 행의 개수가 열의 개수보다 작지 않다는 것을 알고 있습니다. 역시, 다음이기 때문에,

$\mathbf {U} _{1}^{*}\mathbf {U} _{1}=\mathbf {D} ^{-{\frac {1}{2}}}\mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}\mathbf {D} ^{-{\frac {1}{2}}}=\mathbf {D} ^{-{\frac {1}{2}}}\mathbf {D} \mathbf {D} ^{-{\frac {1}{2}}}=\mathbf {I_{1}} ,$

$\mathbf {U} _{1}$에서 열은 직교정규이고 직교정규 기저로 확장될 수 있습니다. 이것은 $\mathbf {U} ={\begin{bmatrix}\mathbf {U} _{1}&\mathbf {U} _{2}\end{bmatrix}}$가 유니태리임을 만족하는 $\mathbf {U} _{2}$를 선택할 수 있음을 의미합니다.

V₁에 대해, 그것을 유니태리로 만들기 위해 V₂를 이미 가집니다. 이제, 다음을 정의합니다:

${\boldsymbol {\Sigma }}={\begin{bmatrix}{\begin{bmatrix}\mathbf {D} ^{\frac {1}{2}}&0\\0&0\end{bmatrix}}\\0\end{bmatrix}},$

여기서 여분의 영 행이 추가되거나 제거되어 영 행의 개수가 U₂의 열의 개수와 같게 만들고, 따라서 ${\boldsymbol {\Sigma }}$의 전체 차원은 $m\times n$과 같습니다. 그런-다음

${\begin{bmatrix}\mathbf {U} _{1}&\mathbf {U} _{2}\end{bmatrix}}{\begin{bmatrix}{\begin{bmatrix}\mathbf {} D^{\frac {1}{2}}&0\\0&0\end{bmatrix}}\\0\end{bmatrix}}{\begin{bmatrix}\mathbf {V} _{1}&\mathbf {V} _{2}\end{bmatrix}}^{*}={\begin{bmatrix}\mathbf {U} _{1}&\mathbf {U} _{2}\end{bmatrix}}{\begin{bmatrix}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}\\0\end{bmatrix}}=\mathbf {U} _{1}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}=\mathbf {M} ,$

이는 원했든 결과입니다:

$\mathbf {M} =\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}.$

논증은 M^⁎M 대신 MM^⁎를 대각화하는 것으로 시작할 수 있습니다 (이것은 MM^⁎와 M^⁎M이 같은 비-영 고윳값을 가짐을 직접적으로 보여줍니다).

Based on variational characterization

특이값은 특정 부분공간에 걸쳐 u와 v의 함수로 고려되는 u^TMv의 최댓값으로 특성화될 수도 있습니다. 특이 벡터는 이들 최댓값이 달성되는 u와 v의 값입니다.

M은 실수 엔트리를 갖는 m × n 행렬을 나타낸다고 놓습니다. S^k−1을 $\mathbb {R} ^{k}$에서 단위 $(k-1)$-구로 놓고, $\sigma (\mathbf {u} ,\mathbf {v} )=\mathbf {u} ^{\textsf {T}}\mathbf {M} \mathbf {v} ,\ \mathbf {u} \in S^{m-1},\mathbf {v} \in S^{n-1}$을 정의합니다.

S^m−1 × Sⁿ⁻¹로 제한된 함수 σ를 생각해 보십시오. S^m−1과 Sⁿ⁻¹ 둘 다는 컴팩트(compact) 집합이므로, 그것들의 곱(product)도 컴팩트입니다. 게다가, σ는 연속적이기 때문에, 그것은 적어도 한 쌍의 벡터 u ∈ S^m−1와 v ∈ Sⁿ⁻¹에 대해 가장 큰 값에 도달합니다. 이 가장 큰 값은 σ₁으로 표시되고 해당 벡터는 u₁과 v₁으로 표시됩니다. σ₁은 σ(u, v)의 가장 큰 값이므로, 그것은 비-음수여야 합니다. 만약 그것이 음수이면, u₁ 또는 v₁의 부호를 변경하는 것은 그것을 양수로 만들고 따라서 더 커집니다.

Statement. u₁, v₁는 해당 특이값 σ₁을 갖는 M의 왼쪽 및 오른쪽-특이 벡터입니다.

Proof. 고윳값의 경우와 유사하게, 두 벡터가 라그랑주 곱셈수 방정식을 만족시킨다는 가정에 의해:

$\nabla \sigma =\nabla \mathbf {u} ^{\textsf {T}}\mathbf {M} \mathbf {v} -\lambda _{1}\cdot \nabla \mathbf {u} ^{\textsf {T}}\mathbf {u} -\lambda _{2}\cdot \nabla \mathbf {v} ^{\textsf {T}}\mathbf {v}$

약간의 대수 후에, 이것은 다음이 됩니다:

${\begin{aligned}\mathbf {M} \mathbf {v} _{1}&=2\lambda _{1}\mathbf {u} _{1}+0\\\mathbf {M} ^{\textsf {T}}\mathbf {u} _{1}&=0+2\lambda _{2}\mathbf {v} _{1}\end{aligned}}$

왼쪽에서 첫 번째 방정식에 $\mathbf {u} _{1}^{\textsf {T}}$를 곱하고 왼쪽에서 두 번째 방정식에 $\mathbf {v} _{1}^{\textsf {T}}$를 곱하고 ||u|| = ||v|| = 1을 고려하는 것은 다음을 제공합니다:

$\sigma _{1}=2\lambda _{1}=2\lambda _{2}.$

이것을 위의 방정식 쌍에 대입하면, 다음을 가집니다:

${\begin{aligned}\mathbf {M} \mathbf {v} _{1}&=\sigma _{1}\mathbf {u} _{1}\\\mathbf {M} ^{\textsf {T}}\mathbf {u} _{1}&=\sigma _{1}\mathbf {v} _{1}\end{aligned}}$

이것은 그 명제를 입증합니다.

각각 u₁과 v₁에 직교하는 정규화된 u, v에 걸쳐 σ(u, v)를 최대화함으로써 더 많은 특이 벡터와 특이값을 찾을 수 있습니다.

실수에서 복소수로의 전환은 고윳값의 경우와 유사합니다.

Calculating the SVD

특이값 분해는 다음 관찰을 사용하여 계산될 수 있습니다:

• M의 왼쪽-특이 벡터는 MM^⁎의 직교정규(orthonormal) 고유벡터(eigenvectors)의 집합입니다.
• M의 오른쪽-특이 벡터는 M^⁎M의 직교정규 고유벡터의 집합입니다.
• M의 비-영 특이값 ($\mathbf {\Sigma }$의 대각선 엔트리에 있음)은 M^⁎M과 MM^⁎ 둘 다의 비-영 고윳값(eigenvalues)의 제곱근입니다.

Numerical approach

행렬 M의 SVD는 전형적으로 2-단계 절차로 계산됩니다. 첫 번째 단계에서, 행렬이 이중대각 행렬(bidiagonal matrix)로 축소됩니다. 이것은 m ≥ n이라고 가정하여 O(mn²) 부동-점 연산 (플롭)을 취합니다. 두 번째 단계는 이중대각 행렬의 SVD를 계산하는 것입니다. 이 단계는 (고윳값 알고리듬과 마찬가지로) 반복 방법으로만 수행될 수 있습니다. 어쨌든, 실제로는 기계 엡실론(machine epsilon)과 같이 특정 정밀도까지 SVD를 계산하는 것으로 충분합니다. 만약 이 정밀도가 일정하다고 고려되면, 두 번째 단계는 O(n) 반복을 취하며, 각 단계의 비용은 O(n) 플롭입니다. 따라서, 첫 번째 단계는 더 비싸고, 전체 비용은 O(mn²) 플롭입니다 (Trefethen & Bau III 1997, Lecture 31).

첫 번째 단계는 특이 벡터가 필요하지 않고 특이값만 필요하다고 가정하여 4mn² − 4n³/3 플롭의 비용으로 하우스홀더 반사(Householder reflections)를 사용하여 수행될 수 있습니다. 만약 m이 n보다 훨씬 크면, 먼저 행렬 M을 QR 분해(QR decomposition)를 갖는 삼각 행렬로 축소하고 그런-다음 하우스홀더 반사를 사용하여 행렬을 이중대각 형식으로 추가로 축소하는 것이 유리합니다; 총 비용은 2mn² + 2n³ 플롭입니다 (Trefethen & Bau III 1997, Lecture 31).

두 번째 단계는 Golub & Kahan (1965)에 의해 처음 설명된 고윳값의 계산을 위한 QR 알고리듬의 변형을 통해 수행될 수 있습니다. LAPACK 서브루틴 DBDSQR은 이 반복 방법을 구현하며, 특이값이 매우 작은 경우를 처리하기 위해 일부 수정을 가집니다 (Demmel & Kahan 1990). 하우스홀더 반사 및, 적절하다면, QR 분해를 사용하는 첫 번째 단계와 함께, 이것은 특이값 분해의 계산을 위한 DGESVD 루틴을 형성합니다.

같은 알고리듬은 GNU Scientific Library (GSL)에 구현되어 있습니다. GSL은 역시 단계2 에서 한-측 야코비 직교화를 사용하는 대안적인 방법을 제공합니다 (GSL Team 2007). 이 방법은 야코비 고윳값 알고리듬(Jacobi eigenvalue algorithm)이 2 × 2 고윳값 방법의 수열을 푸는 방법과 유사하게 2 × 2 SVD 문제의 수열을 해결함으로써 이중대각 행렬의 SVD를 계산합니다 (Golub & Van Loan 1996, §8.6.3). 단계 2의 또 다른 방법은 분할-과-정복 고윳값 알고리듬(divide-and-conquer eigenvalue algorithms)의 아이디어를 사용합니다 (Trefethen & Bau III 1997, Lecture 31).

고윳값 분해를 명시적으로 사용하지 않는 대안적인 방법이 있습니다. 보통 행렬 M의 특이값 문제는 M M^⁎, M^⁎M, 또는 다음을 만족하는 동등한 대칭 고윳값 문제로 변환됩니다:

${\begin{bmatrix}\mathbf {O} &\mathbf {M} \\\mathbf {M} ^{*}&\mathbf {O} \end{bmatrix}}.$

고윳값 분해를 사용하는 접근 방식은 안정적이고 빠르도록 잘 개발된 QR 알고리듬을 기반으로 합니다. 특이값은 실수이고 오른쪽- 및 왼쪽-특이 벡터는 닮음 변환을 형성하기 위해 필요하지 않음에 주목하십시오. 실수 대각 에르미트 행렬(Hermitian matrices)을 찾기 위해 QR 분해와 LQ 분해 사이를 반복적으로 교대로 수행할 수 있습니다. QR 분해는 M ⇒ Q R을 제공하고 R의 LQ 분해는 R ⇒ L P^⁎를 제공합니다. 따라서, 매 반복마다, M ⇒ Q L P^⁎를 가지고, M ⇐ L을 업데이트하고 직교화를 반복합니다. 결국, QR 분해와 LQ 분해 사이의 반복은 왼쪽- 및 오른쪽-유니태리 단일 행렬을 생성합니다. QR 알고리듬은 스펙트럼 이동이나 수축을 사용할 수 있으므로 이 접근 방식은 쉽게 가속화될 수 없습니다. 이것은 닮음 변환을 사용 없이 이동 방법을 쉽게 정의할 수 없기 때문입니다. 어쨌든, 이 반복적 접근 방식은 구현이 매우 간단하므로, 속도가 중요하지 않을 때 좋은 선택입니다. 이 방법은 역시 어떻게 순수 직교/유니태리 변환이 SVD를 얻을 수 있는지에 대한 통찰력을 제공합니다.

Analytic result of 2 × 2 SVD

2 × 2 행렬의 특이값은 해석적으로 찾을 수 있습니다. 행렬을 $\mathbf {M} =z_{0}\mathbf {I} +z_{1}\sigma _{1}+z_{2}\sigma _{2}+z_{3}\sigma _{3}$이라고 놓습니다.

여기서 $z_{i}\in \mathbb {C}$는 행렬을 매겨변수화하는 복소수, I는 항등 행렬이고, $\sigma _{i}$는 파울리 행렬(Pauli matrices)을 나타냅니다. 그런-다음 두 개의 특이값은 다음에 의해 주어집니다:

${\begin{aligned}\sigma _{\pm }&={\sqrt {|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}\pm {\sqrt {(|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2})^{2}-|z_{0}^{2}-z_{1}^{2}-z_{2}^{2}-z_{3}^{2}|^{2}}}}}\\&={\sqrt {|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}\pm 2{\sqrt {(\operatorname {Re} z_{0}z_{1}^{*})^{2}+(\operatorname {Re} z_{0}z_{2}^{*})^{2}+(\operatorname {Re} z_{0}z_{3}^{*})^{2}+(\operatorname {Im} z_{1}z_{2}^{*})^{2}+(\operatorname {Im} z_{2}z_{3}^{*})^{2}+(\operatorname {Im} z_{3}z_{1}^{*})^{2}}}}}\end{aligned}}$

Reduced SVDs

Visualization of Reduced SVD variants. From top to bottom: 1: Full SVD, 2: Thin SVD (remove columns of U not corresponding to rows of V*), 3: Compact SVD (remove vanishing singular values and corresponding columns/rows in U and V*), 4: Truncated SVD (keep only largest t singular values and corresponding columns/rows in U and V*)

응용 분야에서 행렬의 널-공간의 전체 유니태리 분해를 포함하여 전체 SVD가 필요한 것은 매우 이례적입니다. 대신, SVD의 축소된 버전을 계산하는 것으로 충분할 때가 많습니다 (마찬가지로 저장에 있어 더 빠르고 경제적입니다). 다음은 랭크 $r$의 $m\times n$ 행렬 M에 대해 구별될 수 있습니다:

Thin SVD

행렬 M의 얇은, 또는 경제적인-크기의 SVD는 다음에 의해 지정됩니다:

$\mathbf {M} =\mathbf {U} _{k}{\boldsymbol {\Sigma }}_{k}\mathbf {V} _{k}^{*},$

여기서

$k=\operatorname {min} (m,n)$,

행렬 $\mathbf {U} _{k}$와 $\mathbf {V} _{k}$는 $\mathbf {U}$와 $\mathbf {V}$의 처음 $k$개 열만 포함하고, $\mathbf {\Sigma } _{k}$는 $\mathbf {\Sigma }$로부터 처음 $k$개 특이값만 포함합니다. 따라서 행렬 $\mathbf {U} _{k}$는 $m\times k$이고, $\mathbf {\Sigma } _{k}$는 $k\times k$ 대각이고, $\mathbf {V} _{k}^{*}$는 $k\times n$입니다.

얇은 SVD는 k ≪ max(m, n)이면 훨씬 적은 공간과 계산 시간을 사용합니다. 계산에서 첫 번째 단계는 보통 M의 QR 분해이며, 이 경우에서 훨씬 더 빠른 계산을 가능하게 만듭니다.

Compact SVD

$\mathbf {M} =\mathbf {U} _{r}{\boldsymbol {\Sigma }}_{r}\mathbf {V} _{r}^{*}$

$\mathbf {U}$의 $r$ 열 벡터와 비-영 특이값 $\mathbf {\Sigma } _{r}$에 해당하는 $\mathbf {V} ^{*}$의 $r$ 행 벡터만 계산됩니다. $\mathbf {U}$와 $\mathbf {V} ^{*}$의 남아있는 벡터는 계산되지 않습니다. 이것은 r ≪ min(m, n)이면 얇은 SVD보다 더 빠르고 경제적입니다. 따라서 행렬 $\mathbf {U} _{r}$은 $m\times r$이고, $\mathbf {\Sigma } _{r}$은 $r\times r$ 대각이고, $\mathbf {V} ^{*}$은 $r\times n$입니다.

Truncated SVD

많은 응용 분야에서, 비-영 특이값의 개수 $r$은 크기 때문에 Compact SVD도 계산하기에 실용적이지 않습니다. 그러한 경우에서, 가장 작은 특이값은 t ≪ r 비-영 특이값만 계산하기 위해 잘라야 할 수도 있습니다. 잘린 SVD는 더 이상 원래 행렬 M의 정확한 분해가 아니지만, 고정 랭크 $t$의 임의의 행렬에 의한 최적의 낮은-랭크 행렬 근삿값(low-rank matrix approximation) ${\tilde {\mathbf {M} }}$을 제공합니다:

${\tilde {\mathbf {M} }}=\mathbf {U} _{t}{\boldsymbol {\Sigma }}_{t}\mathbf {V} _{t}^{*}$,

여기서 행렬 $\mathbf {U} _{t}$는 $m\times t$, $\mathbf {\Sigma } _{t}$는 $t\times t$이고, $\mathbf {V} _{t}^{*}$는 $t\times n$입니다. $\mathbf {U}$의 $t$개의 열 벡터와 $t$개의 가장 큰 특이값 $\mathbf {\Sigma } _{t}$에 해당하는 $\mathbf {V} ^{*}$의 $t$개의 행 벡터만 계산됩니다. 이것은 t ≪ r이면 컴팩트 SVD보다 훨씬 빠르고 경제적일 수 있지만, 완전하게 다른 수치 해결기의 도구모음이 필요합니다.

행렬 M의 무어-펜로즈 역(Moore–Penrose inverse)에 대한 근사가 필요한 응용 분야에서, M의 가장 작은 특이값이 중요하며, 이는 가장 큰 특이값에 비해 계산하기가 더 어렵습니다.

잘린 SVD는 잠재 의미론적 인덱싱(latent semantic indexing)에서 사용됩니다.

Norms

Ky Fan norms

M의 가장 큰 $k$개 특이값의 합은 M의 행렬 노름(matrix norm), 판지(Ky Fan) $k$-노름입니다.

판지 노름 중 첫 번째, 판지 1-노름은 $\mathbf {K} ^{m}$ 및 $\mathbf {K} ^{n}$의 유클리드 노름에 관한 선형 연산자로서 M의 연산자 노름(operator norm)과 같습니다. 다시 말해서, 판지 1-노름은 표준 ℓ² 유클리드 안의 곱에 의해 유도된 연산자 노름입니다. 이러한 이유로, 그것은 역시 연산자 2-노름이라고 불립니다. 판지 1-노름과 특이값 사이의 관계를 쉽게 확인할 수 있습니다. 그것은 일반적으로 (무한 차원일 수도 있는) 힐베르트 공간 위에 경계진 연산자 M에 대해 참입니다:

$\|\mathbf {M} \|=\|\mathbf {M} ^{*}\mathbf {M} \|^{\frac {1}{2}}$

그러나, 행렬 경우에서, $\left(\mathbf {M} ^{*}\mathbf {M} \right)^{\frac {1}{2}}$은 행렬 노름(normal matrix)이므로, $\|\mathbf {M} ^{*}\mathbf {M} \|^{\frac {1}{2}}$은 $\left(\mathbf {M} ^{*}\mathbf {M} \right)^{\frac {1}{2}}$의 가장 큰 고윳값, 즉, M의 가장 큰 고윳값입니다.

모든 특이값의 합, 판지 노름의 마지막은 $\|\mathbf {M} \|={\mbox{Tr}}\left[\mathbf {M} ^{*}\mathbf {M} ^{\frac {1}{2}}\right]$에 의해 정의되는 대각합 노름(trace norm, '핵 규범'이라고도 알려져 있음)입니다 ($\mathbf {M} ^{*}\mathbf {M}$의 고윳값은 특이값의 제곱입니다).

Hilbert–Schmidt norm

특이값은 연산자의 공간 위에 또 다른 노름과 관련됩니다. 다음에 의해 정의되는 n × n 행렬 위에 힐베르트-슈미트(Hilbert–Schmidt) 안의 곱을 생각해 보십시오:

$\langle \mathbf {M} ,\mathbf {N} \rangle =\operatorname {tr} \left(\mathbf {N} ^{*}\mathbf {M} \right).$

따라서 유도된 노름은 다음입니다:

$\|\mathbf {M} \|={\sqrt {\langle \mathbf {M} ,\mathbf {M} \rangle }}={\sqrt {\operatorname {tr} \left(\mathbf {M} ^{*}\mathbf {M} \right)}}.$

대각합은 유니태리 동등성 아래에서 불변이기 때문에, 이것은 다음임을 보여줍니다:

$\|\mathbf {M} \|={\sqrt {\sum _{i}\sigma _{i}^{2}}}$

여기서 σ_i는 M의 특이값입니다. 이것은 M의 프로베니우스 노름(Frobenius norm), 샤텐 2-노름(Schatten 2-norm), 또는 힐베르트-슈미트 노름(Hilbert–Schmidt norm)이라고 불립니다. 직접 계산에 따르면 M = (m_ij)의 프로베니우스 노름은 다음과 일치합니다:

${\sqrt {\sum _{ij}|m_{ij}|^{2}}}.$

게다가, 프로베니우스 노름과 대각합 노름 (핵 노름)은 샤텐 노름(Schatten norm)의 특별한 경우입니다.

Variations and generalizations

Scale-invariant SVD

행렬 A의 특이값은 고유하게 정의되고 A의 왼쪽 및/또는 오른쪽 유니태리 변환에 관해 불변입니다. 다시 말해서, 유니태리 U와 V에 대한 UAV의 특이값은 A의 특이값과 같습니다. 이것은 유클리드 거리와 회전에 관한 불변을 보존해야 하는 응용 분야에 대해 중요한 속성입니다.

스케일-불변 SVD(Scale-Invariant SVD, 또는 SI-SVD)는 그것의 고유하게-결정된 특이값이 A의 대각 변환에 관해 불변이라는 점을 제외하면 기존 SVD와 유사합니다. 다시 말해, 역 대각 행렬 D와 E에 대한 DAE의 특이값은 A의 특이값과 같습니다. 이것은 변수에 대한 단위 선택 (예를 들어, 메트릭 대 영국식 단위)에 불변성이 필요한 응용 분야에 중요한 속성입니다.

Bounded operators on Hilbert spaces

인수분해 M = UΣV^⁎는 분리-가능한 힐베르트 공간 H의 경계진 연산자(bounded operator) M으로 확장될 수 있습니다. 즉, 임의의 경계진 연산자 M에 대해, 부분 등거리변환(partial isometry) $\mathbf {U}$, 유니태리 $\mathbf {V}$, 측정 공간 (X, μ), 및 다음임을 만족하는 비-음수 측정-가능 f가 존재합니다:

$\mathbf {M} =\mathbf {U} T_{f}\mathbf {V} ^{*}$

여기서 $T_{f}$는 L²(X, μ) 위에 f에 의한 곱셈입니다.

이것은 위의 행렬적 경우에 대한 선형 대수적 논증을 모방함으로써 표시될 수 있습니다. $\mathbf {V} T_{f}\mathbf {V} ^{*}$는 자기-인접 연산자(self-adjoint operators)에 대한 보렐 함수형 미적분(Borel functional calculus)에서 제공되는 것처럼 $\mathbf {M} ^{*}\mathbf {M}$의 고유한 양의 제곱근입니다. $\mathbf {U}$가 유니태리일 필요가 없는 이유는, 유한-차원의 경우와 달리, 비-자명한 커널을 갖는 등거리변환 $U_{1}$이 주어지면, 적합한 $U_{2}$가 다음이 유니태리 연산자임을 만족하게 발견되지 않을 수 있기 때문입니다:

${\begin{bmatrix}U_{1}\\U_{2}\end{bmatrix}}$

행렬에 대한 것처럼, 특이값 인수분해는 연산자에 대해 극 분해(polar decomposition)와 동등합니다: 간단히 다음을 쓸 수 있고,

$\mathbf {M} =\mathbf {U} \mathbf {V} ^{*}\cdot \mathbf {V} T_{f}\mathbf {V} ^{*}$

$\mathbf {U} \mathbf {V} ^{*}$가 여전히 부분 등거리변환이고 반면에 $\mathbf {V} T_{f}\mathbf {V} ^{*}$는 양수임에 유의하십시오.

Singular values and compact operators

특이값과 왼쪽/오른쪽-특이 벡터의 개념은 그것들이 이산 스펙트럼을 가지기 때문에 힐베르트 공간 위에 컴팩트 연산자로 확장될 수 있습니다. 만약 T가 컴팩트이면, 그것의 스펙트럼에서 모든 각 비-영 λ는 고윳값입니다. 게다가, 컴팩트 자기-인접 연산자는 그것의 고유벡터에 의해 대각화될 수 있습니다. 만약 M이 컴팩트이면, M^⁎M도 마찬가지입니다. 대각화 결과를 적용하여, 양의 제곱근 T_f 의 유니태리 이미지는 엄격하게 양의 고윳값 {σ_i}에 해당하는 직교정규 고유벡터 {e_i}의 집합을 가집니다. 임의의 ψ ∈ H에 대해,

$\mathbf {M} \psi =\mathbf {U} T_{f}\mathbf {V} ^{*}\psi =\sum _{i}\left\langle \mathbf {U} T_{f}\mathbf {V} ^{*}\psi ,\mathbf {U} e_{i}\right\rangle \mathbf {U} e_{i}=\sum _{i}\sigma _{i}\left\langle \psi ,\mathbf {V} e_{i}\right\rangle \mathbf {U} e_{i},$

여기서 급수는 H 위에 노름 토폴로지로 수렴합니다. 이것이 유한-차원 사례의 표현과 얼마나 유사한지 주목하십시오. σ_i는 M의 특이값이라고 불립니다. {Ue_i} (각각 {Ve_i})는 M의 왼쪽-특이 (각각 오른쪽-특이) 벡터로 여길 수 있습니다.

힐베르트 공간 위에 컴팩트 연산자는 균등 연산자 토폴로지에서 유한-랭크 연산자(finite-rank operators)의 클로저입니다. 위의 급수 표현은 그러한 표현을 명시적으로 제공합니다. 이에 대한 즉각적인 결과는 다음입니다:

Theorem. M이 컴팩트인 것과 M^⁎M이 컴팩트인 것은 필요충분 조건입니다.

History

특이값 분해는 원래 미분 기하학자들에 의해 개발되었으며, 그들은 실수 쌍선형 형식(bilinear form)이 그것이 작용하는 두 공간의 독립적인 직교 변환에 의해 또 다른 형식과 같게 만들 수 있는지 여부를 확인하기를 원했습니다. 에우제니오 벨트라미(Eugenio Beltrami)와 카미유 조르당(Camille Jordan)은 각각 1873년과 1874년에 행렬로 표현된 쌍선형 형식의 특이값이 직교 치환 아래에서 쌍선형 형식에 대한 불변(invariants)의 완비 집합(complete set)을 형성한다는 것을 독립적으로 발견했습니다. 제임스 조지프 실베스터(James Joseph Sylvester)도 1889년에 벨트라미(Beltrami)와 조르당(Jordan) 둘 다와는 보기에 독립적으로 실수 정사각 행렬에 대한 특이값 분해에 도달했습니다. 실베스터는 특이값을 행렬 A의 정식의 곱셈수(canonical multipliers)라고 불렀습니다. 특이값 분해를 독립적으로 발견한 네 번째 수학자는 1915년에 오톤(Autonne)이며, 그는 극 분해(polar decompositio)를 통해 그것에 도달했습니다. 직사각 행렬과 복소수 행렬에 대한 특이값 분해의 첫 번째 증명은 1936년 Carl Eckart와 Gale J. Young에 의한 것으로 보입니다; 그들은 그것을 에르미트 행렬(Hermitian matrices)에 대한 주요 축(principal axis) 변환의 일반화로 보았습니다.

1907년에 에르하르트 슈미트(Erhard Schmidt)는 적분 연산자 (이는 일부 약한 기술적 가정 아래에서 컴팩트임)에 대한 특이값의 아날로그를 정의했습니다; 그는 유한 행렬의 특이값에 대한 병렬 작업을 인식하지 못한 것 같습니다. 이 이론은 1910년에 에밀 피카르(Émile Picard)에 의해 더욱 발전되었으며, 그는 처음으로 숫자를 $\sigma _{k}$ 특이값(singular values, 또는 프랑스어로, valeurs singulières)이라고 불렀습니다.

SVD를 계산하는 실용적인 방법은 1954–1955년에서 Kogbetliantz와 1958년에서 Hestenes로 거슬러 올라가며, 이는 평면 회전 또는 기븐스 회전(Givens rotations)을 사용하는 야코비 고윳값 알고리듬(Jacobi eigenvalue algorithm)과 매우 유사합니다. 어쨌든, 이것들은 1965년에 출판된 Gene Golub와 윌리엄 카한(William Kahan)의 방법으로 대체되었으며, 이는 하우스홀더 변환(Householder transformations) 또는 반사를 사용합니다. 1970년에, Golub과 Christian Reinsch는 오늘날에도 여전히 가장 많이 사용되는 Golub/Kahan 알고리듬의 변형을 발표했습니다.

See also

• Canonical correlation
• Canonical form
• Correspondence analysis (CA)
• Curse of dimensionality
• Digital signal processing
• Dimensionality reduction
• Eigendecomposition of a matrix
• Empirical orthogonal functions (EOFs)
• Fourier analysis
• Generalized singular value decomposition
• Inequalities about singular values
• K-SVD
• Latent semantic analysis
• Latent semantic indexing
• Linear least squares
• List of Fourier-related transforms
• Locality-sensitive hashing
• Low-rank approximation
• Matrix decomposition
• Multilinear principal component analysis (MPCA)
• Nearest neighbor search
• Non-linear iterative partial least squares
• Polar decomposition
• Principal component analysis (PCA)
• Schmidt decomposition
• Smith normal form
• Singular value
• Time series
• Two-dimensional singular-value decomposition (2DSVD)
• von Neumann's trace inequality
• Wavelet compression

References

• Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1st ed.), Chapman and Hall/CRC, ISBN 978-1420095388
• Chicco, D; Masseroli, M (2015). "Software suite for gene and protein annotation prediction and similarity search". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 12 (4): 837–843. doi:10.1109/TCBB.2014.2382127. hdl:11311/959408. PMID 26357324. S2CID 14714823.
• Trefethen, Lloyd N.; Bau III, David (1997). Numerical linear algebra. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-361-9.
• Demmel, James; Kahan, William (1990). "Accurate singular values of bidiagonal matrices". SIAM Journal on Scientific and Statistical Computing. 11 (5): 873–912. CiteSeerX 10.1.1.48.3740. doi:10.1137/0911052.
• Golub, Gene H.; Kahan, William (1965). "Calculating the singular values and pseudo-inverse of a matrix". Journal of the Society for Industrial and Applied Mathematics, Series B: Numerical Analysis. 2 (2): 205–224. Bibcode:1965SJNA....2..205G. doi:10.1137/0702016. JSTOR 2949777.
• Golub, Gene H.; Van Loan, Charles F. (1996). Matrix Computations (3rd ed.). Johns Hopkins. ISBN 978-0-8018-5414-9.
• GSL Team (2007). "§14.4 Singular Value Decomposition". GNU Scientific Library. Reference Manual.
• Halldor, Bjornsson and Venegas, Silvia A. (1997). "A manual for EOF and SVD analyses of climate data". McGill University, CCGCR Report No. 97-1, Montréal, Québec, 52pp.
• Hansen, P. C. (1987). "The truncated SVD as a method for regularization". BIT. 27 (4): 534–553. doi:10.1007/BF01937276. S2CID 37591557.
• Horn, Roger A.; Johnson, Charles R. (1985). "Section 7.3". Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6.
• Horn, Roger A.; Johnson, Charles R. (1991). "Chapter 3". Topics in Matrix Analysis. Cambridge University Press. ISBN 978-0-521-46713-1.
• Samet, H. (2006). Foundations of Multidimensional and Metric Data Structures. Morgan Kaufmann. ISBN 978-0-12-369446-1.
• Strang G. (1998). "Section 6.7". Introduction to Linear Algebra (3rd ed.). Wellesley-Cambridge Press. ISBN 978-0-9614088-5-5.
• Stewart, G. W. (1993). "On the Early History of the Singular Value Decomposition". SIAM Review. 35 (4): 551–566. CiteSeerX 10.1.1.23.1831. doi:10.1137/1035134. hdl:1903/566. JSTOR 2132388.
• Wall, Michael E.; Rechtsteiner, Andreas; Rocha, Luis M. (2003). "Singular value decomposition and principal component analysis". In D.P. Berrar; W. Dubitzky; M. Granzow (eds.). A Practical Approach to Microarray Data Analysis. Norwell, MA: Kluwer. pp. 91–109.
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 2.6", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8

External links

• Online SVD calculator