Invariant (mathematics)

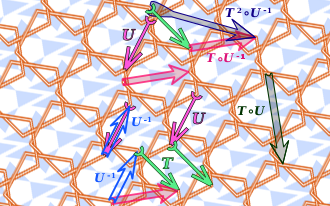
수학(mathematics)에서, 불변(invariant)은 특정 유형의 연산(operations) 또는 변환(transformations)이 대상에 적용된 후 변하지 않고 남아있는 수학적 대상(mathematical object) (또는 수학적 대상의 클래스(class))의 속성입니다.^[1]^[2] 대상의 특정 클래스와 변환의 특정 유형은 보통 그 용어가 사용되는 문맥에 의해 암시됩니다. 예를 들어, 삼각형의 넓이(area)는 유클리드 평면(Euclidean plane)의 등거리 변환(isometry)에 관해 불변입니다. 어구 변환 "아래에서 불변" 및 변환"에 대한 불변"은 둘 다 사용됩니다. 보다 일반적으로, 동치 관계(equivalence relation)에 관한 불변은 각 동치 클래스에 대한 일정한 속성입니다.^[3]

불변은 기하학(geometry), 토폴로지(topology), 대수학(algebra), 및 이산 수학(discrete mathematics)과 같은 수학의 다양한 영역에서 사용됩니다. 몇 가지 중요한 변환의 클래스는 그것들이 변경되지 않고 남아있는 불변에 의해 정의됩니다. 예를 들어, 등각 맵(conformal map)은 각도(angle)를 보존하는 평면의 변환으로 정의됩니다. 불변의 발견은 수학적 대상을 분류하는 과정에서 중요한 단계입니다.^[2]^[3]

Examples

불변성의 간단한 예제는 세기(count) 위한 우리의 능력에서 표현됩니다. 임의의 종류의 대상의 유한 집합(finite set)에 대해, 집합(set)에서 대상을 세는 순서(order)에 관계없이 항상 도달하는 숫자가 있습니다. 수량—세는 숫자(cardinal number)—은 집합과 결합되고 세는 과정 아래에서 불변입니다.

항등식(identity)은 그것의 변수의 모든 값에 대해 참으로 남아있는 방정식입니다. 역시 그것들 변수의 값이 변경될 때 참으로 남아있는 부등식(inequalities)이 있습니다.

숫자 직선(number line) 위의 두 점 사이의 거리(distance)는 두 숫자에 같은 양을 더해도 변하지 않습니다. 다른 한편으로, 곱셈(multiplication)은 이 같은 속성을 가지지 않는데, 왜냐하면 거리는 곱셈 아래에서 불변이 아니기 때문입니다.

거리의 각도(angle)와 비율(ratio)은 스케일링(scalings), 회전(rotation), 평행이동(translation), 및 반사(reflection) 아래에서 불변입니다. 이들 변환은 삼각법(trigonometry)의 기초가 되는 닮은(similar) 모양을 생성합니다. 대조적으로, 각도와 비율은 비-균등 스케일링 (예를 들어, 늘이기) 아래에서 불변이 아닙니다. 삼각형의 내각의 합 (180°)은 모든 위의 연산 아래에서 불변입니다. 또 다른 예제로, 모든 원(circle)은 닮았습니다: 그것들은 서로 변환될 수 있고 지름(diameter)에 대한 원주(circumference)의 비율은 불변입니다 (그리스 문자 π (파이)로 표시됩니다).

일부보다 복잡한 예제:

복소수(complex number)의 실수 부분(real part)과 절댓값(absolute value)은 복소 켤레(complex conjugation) 아래에서 불변입니다.
다항식(polynomial)의 차수(degree)는 변수의 선형 변경 아래에서 불변입니다.
토폴로지적 대상의 차원(dimension)과 호몰로지 그룹(homology group)은 위상동형(homeomorphism) 아래에서 불변입니다.^[4]
동적 시스템(dynamical system)의 고정된 점(fixed points)의 숫자는 많은 수학적 연산 아래에서 불변입니다.
유클리드 거리는 직교 변환(orthogonal transformation) 아래에서 불변입니다.
유클리드 넓이는 행렬식(determinant) $\pm1$ 을 가지는 선형 맵(linear map) 아래에서 불변입니다 (Equiareal map § Linear transformations를 참조하십시오).
투영 변환(projective transformation)의 일부 불변은 셋 이상 점의 공선성(collinearity), 셋 이상의 공점(concurrency), 원뿔 단면(conic section), 교차-비율(cross-ratio)을 포함합니다.^[5]
정사각 행렬(square matrix)의 행렬식(determinant), 대각합(trace), 및 고유벡터(eigenvectors)와 고윳값(eigenvalues)은 기저의 변경(changes of basis) 아래에서 불변입니다. 다시 말해서, 행렬의 스펙트럼(spectrum of a matrix)은 기저의 변경 아래에서 불변입니다.
텐서(tensors)의 주요 불변은 좌표 시스템의 회전에 따라 변하지 않습니다 (텐서의 불변(Invariants of tensors)을 참조하십시오).
행렬(matrix)의 특이 값(singular values)은 직교 변환 아래에서 불변입니다.
르베그 측정(Lebesgue measure)은 평행이동 아래에서 불변입니다.
확률 분포(probability distribution)의 분산(variance)은 실수 직선(real line)의 평행이동 아래에서 불변입니다; 따라서 확률 변수(random variable)의 분산은 상수의 덧셈 후에 변경되지 않습니다.
변환의 고정 점(fixed points)은 변환 아래에서 불변인 도메인(domain)에서 원소입니다. 응용 프로그램에 따라 해당 변환과 관련하여 대칭이라고 할 수 있습니다. 예를 들어, 평행이동 대칭을 가진 객체는 특정 번역에서 불변입니다. 그것들은, 응용에 따라, 해당 변환에 관해 대칭적(symmetric)이라고 불릴 수 있습니다. 예를 들어, 평행이동적 대칭(translational symmetry)을 갖는 대상은 특정 평행이동 아래에서 불변입니다.
2-차원 리만 매니폴드(Riemannian manifold) $(M,g)$ 의 가우스 곡률 $K$ 의 적분 ${\textstyle \int _{M}K\,d\mu }$ 은 리만 메트릭(Riemannian metric) $g$ 의 변경 아래에서 불변입니다. 이것이 가우스–보네 정리(Gauss–Bonnet theorem)입니다.
미분 방정식(differential equations)에 대해 미분 불변(differential invariant)^[6]

MU puzzle

MU 퍼즐(MU puzzle)은 불변을 결정하는 것이 불가능성 증명(impossibility proof)에 대해 사용의 논리적 문제의 좋은 예제입니다.^[7] 퍼즐은 단어 MI로 시작하여 각 단계에서 다음 변환 규칙 중 하나를 사용하여 단어 MU로 변환하도록 요청합니다:

만약 문자열이 I로 끝나면, U는 덧붙여질 수 있습니다 (xI → xIU)
M 후의 문자열은 완전하게 복제될 수 있습니다 (Mx → Mxx)
임의의 셋의 연속되는 I (III)는 단일 U로 대체될 수 있습니다 (xIIIy → xUy)
임의의 둘의 연속되는 U는 제거될 수 있습니다 (xUUy → xy)

예제 유도 (적용된 규칙을 나타내는 위첨자를 가짐)는 다음입니다:

MI →² MII →² MIIII →³ MUI →² MUIUI →¹ MUIUIU →² MUIUIUUIUIU →⁴ MUIUIIUIU → ...

이에 비추어 볼 때, 우리는 오직 이들 네 가지 변환 규칙을 사용하여 MI를 MU로 변환하는 것이 가능한지 궁금할 수 있습니다. 우리는 이들 변환 규칙을 문자열에 적용하는 데 많은 시간을 소모할 수 있습니다. 어쨌든, 모든 규칙에 대해 불변인 (즉, 규칙 중 어느 것에도 변경되지 않음) 속성(property)을 찾는 것이 더 빠를 수 있고, MU에 도달하는 것이 불가능함을 시연합니다. 논리적인 관점에서 퍼즐을 봄으로써, 우리는 임의의 I를 제거하는 유일한 방법이 문자열에 셋의 연속적인 I를 가지는 것임을 인식할 수 있습니다. 이것은 다음 불변을 고려하는 것을 흥미롭게 만듭니다:

문자열에서 I의 개수가 3의 배수가 아닙니다.

이것은 만약 각 변환 규칙에 대해 다음이 유지되면 그 문제에 대한 불변입니다: 만약 불변이 규칙을 적용하기 전에 유지되었다면, 그것은 역시 규칙을 적용 후에 유지될 것입니다. I와 U의 개수에 대한 규칙을 적용한 순 효과를 보면, 우리는 이것이 실제로 모든 규칙에 대한 경우임을 알 수 있습니다:

Rule	#I's	#U's	Effect on invariant
1	+0	+1	Number of I's is unchanged. If the invariant held, it still does.
2	×2	×2	If n is not a multiple of 3, then 2×n isn't either. The invariant still holds.
3	−3	+1	If n is not a multiple of 3, n−3 isn't either. The invariant still holds.
4	+0	−2	Number of I's is unchanged. If the invariant held, it still does.

위의 테이블은 규칙이 각 가능한 변환 규칙에 대해 유지된다는 것을 분명히 보여주며, 이것은 어떤 상태에서 어떤 규칙 하나를 선택하든 규칙을 적용하기 전에 I의 개수가 3의 배수가 아닌 경우에는 변경되으면, 그것은 나중에도 적용되지 않습니다.

시작하는 문자열 MI에 하나의 I이 있고, 3의 배수가 아닌 하나가 있다고 주어지면, 우리는 그때에 MI에서 MU로 가는 것이 불가능하다는 결론을 내릴 수 있습니다 (왜냐하면 I의 개수가 결코 3의 배수가 아닐 것이기 때문입니다).

Invariant set

매핑 T: U → U의 도메인 U의 부분집합(subset) S는 $x\in S\implies T(x)\in S$ 일 때 매핑 아래에서 불변 집합입니다. S의 원소(elements)는 심지어 집합 S가 U의 거듭제곱 집합(power set)에서 고정될지라도 고정된(fixed) 것이 아님을 주목하십시오. (일부 저자는 이들 경우 사이를 구별하기 위해 용어 집합별 불변,^[8] 대. 점별 불변을^[9] 사용합니다.) 예를 들어, 원은 원의 중심에 대한 회전(rotation) 아래에서 평면의 불변 부분집합입니다. 게다가, 원뿔형 표면(conical surface)은 공간의 중심-닮음(homothety) 아래에서 집합으로 불변입니다.

연산 T의 불변 집합은 역시 T 아래에서 안정적이라고 말합니다. 예를 들어, 그룹 이론(group theory)에서 매우 중요한 정규 부분-그룹(normal subgroup)은 주변 그룹(group)의 안의 자기동형(inner automorphism) 아래에서 안정적인 그것들의 부분그룹(subgroup)입니다.^[10]^[11]^[12] 선형 대수(linear algebra)에서, 만약 선형 변환(linear transformation) T가 고유벡터(eigenvector) v를 가지면 0과 v를 통과하는 직선이 T 아래에서 불변 집합이며, 이 경우에서 고유벡터는 안정적인 불변 부분공간(invariant subspace)에 걸쳐 있습니다.

T가 비틀림 변위(screw displacement)일 때, 비틀림 축(screw axis)은 불변 직선이지만, 피치(pitch)가 비-영이면 T는 고정점을 가지지 않습니다.

Formal statement

불변의 개념은 수학에서 그룹 동작(group action), 표시, 및 변형을 통한 세 가지 다른 방법으로 공식화됩니다.

Unchanged under group action

첫째, 만약 우리가 수학적 대상 (또는 대상의 집합) X에 작용하는(acting) 그룹 G를 가지면, 우리는 어떤 점 x가 변경되지 않는지, 그룹 동작 아래에서, 또는 그룹의 원소 g 아래에서 "불변"인지를 물어볼 수 있습니다.

자주 우리는 집합 X에 작용하는 그룹을 가질 것이며, 이 그룹은 우리에게 결합된 집합 F(X)에서 어떤 대상이 불변인지 결정하도록 남겨 놓습니다. 예를 들어, 한 점에 대한 평면에서 회전은 그것이 회전하는 점을 불변으로 남겨 놓고, 반면에 평면에서 평행이동은 임의의 점을 불변으로 남겨두지 않지만, 모든 직선을 평행이동 방향에 평행한 직선으로 남겨 둡니다. 형식적으로, 평면 P에서 직선 집합을 L(P)로 정의합니다; 그런-다음 평면의 강성 운동(rigid motion)은 직선을 직선으로 취하고 – 강체 운동의 그룹은 직선의 집합에 작용합니다 – 우리는 어떤 직선이 작용에 의해 변경되지 않는지 질문할 수 있습니다.

보다 중요하게, 우리는 "평면에서 원의 반지름"과 같은, 집합에 대한 함수를 정의할 수 있고, 그런-다음 이 함수가 강체 운동과 같은 그룹 동작 아래에서 불변인지를 물어볼 수 있습니다.

불변의 개념에 대한 이중은 공불변(coinvariant)하며, 역시 궤도로 알려져 있으며, 이것은 합동(congruence): : 그룹 동작에 의해 서로 취할 수 있는 대상의 개념을 공식화합니다. 예를 들어, 평면의 강체 운동의 그룹 아래에서, 삼각형의 둘레(perimeter)는 불변이고, 반면에 주어진 삼각형에 합동인 삼각형 집합은 공불변입니다.

이것들은 다음과 같이 연결됩니다: 불변은 공불변 위에 상수이지만 (예를 들어, 합동 삼각형은 같은 둘레를 가짐), 하나의 불변의 값에서 일치하는 두 대상은 합동일 수도 있고 그렇지 않을 수도 있습니다 (예를 들어, 같은 둘레를 갖는 두 삼각형이 합동일 필요는 없습니다). 분류 문제(classification problem)에서, 우리는 두 대상이 이 불변 집합에 대해 같은 값을 가지면, 그것들이 합동임을 만족하는 불변의 완전 집합(complete set of invariants)을 찾기 위해 추구할 수 있습니다.

예를 들어, 모든 세 변이 같음을 만족하는 삼각형은 SSS 합동(SSS congruence)을 통해 강체 운동 아래에서 합동이고, 따라서 모든 세 변의 길이는 삼각형에 대해 불변의 완전 집합을 형성합니다. 삼각형의 세 각도 측정은 역시 강체 운동 아래에서 불변이지만, 비-합동 삼각형이 같은 각도 측정을 공유할 수 있으므로 완전 집합을 형성하지 않습니다. 어쨌든, 만약 우리가 강체 운동에 추가하여 스케일링을 허용하면 AAA 닮음 기준은 이것이 불변의 완전 집합임을 보여줍니다.

Independent of presentation

둘째, 함수는 수학적 대상의 일부 표시 또는 분해의 관점에서 정의될 수 있습니다; 예를 들어, 세포 복합체(cell complex)의 오일러 특성(Euler characteristic)은 각 차원에 있는 세포의 숫자의 교대하는 합으로 정의됩니다. 우리는 세포 복합체 구조를 잊을 수 있고 놓여있는 토폴로지적 공간(topological space) (매니폴드(manifold))에서 오직 볼 수 있습니다 – 다른 세포 복합체가 같은 놓여있는 매니폴드를 제공하기 때문에, 우리는 만약 함수가 표시의 선택과 독립적인지 물을 수 있으며, 이 경우에서 그것은 본질적으로 정의된 불변입니다. 이것은 오일러 특성에 대한 경우이고, 불변을 정의하고 계산하는 일반적인 방법은 주어진 표시에 대해 불변을 정의는 것이고, 그런-다음 그것들이 표시의 선택과 독립임을 보여주는 것입니다. 이러한 의미에서 그룹 동작의 개념은 없음을 주목하십시오.

가장 공통 예제는 다음입니다:

좌표 차트의 관점에서 매니폴드의 표시(presentation of a manifold) – 불변은 좌표의 변경(change of coordinates) 아래에서 변경되지 않아야 합니다.
오일러 특성에 대해 논의할 때, 다양한 매니폴드 분해(manifold decomposition).
그룹의 표시(presentation of a group)의 불변.

Unchanged under perturbation

셋째, 대수적 기하학(algebraic geometry)과 미분 기하학(differential geometry)에서 흔히 볼 수 있는 것처럼, 만약 우리가 가족에서 변하는 대상을 연구하면, 우리는 섭동 아래에서 속성이 변경되지 않으면 (예를 들어, 만약 대상이 가족에서 일정하거나 메트릭의 변경 아래에서 불면이면) 질문할 수 있습니다.

Invariants in computer science

컴퓨터 과학(computer science)에서, 우리는 프로그램의 실행 동안, 또는 프로그램의 일부를 실행하는 동안 참이라고 믿을 수 있는 불변을 만날 수 있습니다. 그것은 실행의 특정 단계 동안 항상 참으로 유지되는 논리적 주장(logical assertion)입니다. 예를 들어, 루프 불변(loop invariant)은 모든 각 루프의 실행의 시작과 끝에서 참인 조건입니다.

불변은 컴퓨터 프로그램이 올바른지 여부를 추론할 때 특히 유용합니다. 컴파일러 최적화(optimizing compiler) 이론, 계약에 의한 설계(design by contract)의 방법론, 및 프로그램 정확성(program correctness)을 결정하기 위한 형식적 방법(formal methods)은 모두 불변에 크게 의존합니다.

프로그래머는 종종 그들의 코드에서 불변을 명시적으로 만들기 위해 주장(assertions)을 사용합니다. 일부 객체 지향(object oriented) 프로그래밍 언어(programming language)는 클래스 불변(class invariant)을 지정하기 위한 특수 구문을 가집니다.

Automatic invariant detection in imperative programs

추상 해석(Abstract interpretation) 도구는 주어진 명령형 컴퓨터 프로그램의 단순 불변을 계산할 수 있습니다. 찾을 수 있는 속성의 종류는 사용된 추상 도메인(abstract domains)에 따라 다릅니다. 전형적인 예제 속성은 0<=x<1024와 같은 단일 정수 변수 범위, 0<=i-j<2*n-1과 같은 여러 변수 사이의 관계, y%4==0과 같은 모듈러스 정보입니다. 학술 연구 프로토타입은 역시 포인터 구조의 단순한 속성을 고려합니다.^[13]

보다 정교한 불변은 일반적으로 수동으로 제공되어야 합니다. 특히, 호어 계산법(the Hoare calculus)을 사용하여 명령형 프로그램을 검증할 때,^[14] 루프 불변은 프로그램에서 각 루프에 대해 수동으로 제공되어야 하며, 이 접근 방식이 대부분의 프로그램에 대해 일반적으로 비실용적인 이유 중 하나입니다.

위의 MU 퍼즐(MU puzzle) 예제의 문맥에서, MI에서 MU로의 유도가 오직 규칙 1–4를 사용하여 불가능함을 감지할 수 있는 현재 일반적인 자동화된 도구가 없습니다. 어쨌든, 한번 문자열에서 그것의 "I"의 개수로의 추상화가 손으로 만들어져 왔으면, 예를 들어 다음 C 프로그램으로 이어지는, 추상 해석 도구는 ICount%3가 0이 될 수 없고, 따라서 "while"-루프가 종료되지 않을 것임을 탐지할 수 있습니다.

void MUPuzzle(void) {
    volatile int RandomRule;
    int ICount = 1, UCount = 0;
    while (ICount % 3 != 0)                         // non-terminating loop
        switch(RandomRule) {
        case 1:                  UCount += 1;   break;
        case 2:   ICount *= 2;   UCount *= 2;   break;
        case 3:   ICount -= 3;   UCount += 1;   break;
        case 4:                  UCount -= 2;   break;
        }                                          // computed invariant: ICount % 3 == 1 || ICount % 3 == 2
}

Notes

^ "Invariant Definition (Illustrated Mathematics Dictionary)". www.mathsisfun.com. Retrieved 2019-12-05.
^ ^a ^b Weisstein, Eric W. "Invariant". mathworld.wolfram.com. Retrieved 2019-12-05.
^ ^a ^b "Invariant – Encyclopedia of Mathematics". www.encyclopediaofmath.org. Retrieved 2019-12-05.
^ Fraleigh (1976, pp. 166–167)
^ Kay (1969, pp. 219)
^ Differential Invariants for Differential Equations by André Platzer
^ Hofstadter, Douglas R. (1999) [1979], Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, ISBN 0-465-02656-7 Here: Chapter I.
^ Barry Simon. Representations of Finite and Compact Groups. American Mathematical Soc. p. 16. ISBN 978-0-8218-7196-6.
^ Judith Cederberg (1989). A Course in Modern Geometries. Springer. p. 174. ISBN 978-1-4757-3831-5.
^ Fraleigh (1976, p. 103)
^ Herstein (1964, p. 42)
^ McCoy (1968, p. 183)
^ Bouajjani, A.; Drǎgoi, C.; Enea, C.; Rezine, A.; Sighireanu, M. (2010). "Invariant Synthesis for Programs Manipulating Lists with Unbounded Data" (PDF). Proc. CAV. doi:10.1007/978-3-642-14295-6_8.
^ Hoare, C. A. R. (October 1969). "An axiomatic basis for computer programming" (PDF). Communications of the ACM. 12 (10): 576–580. doi:10.1145/363235.363259. S2CID 207726175. Archived from the original (PDF) on 2016-03-04.

References

Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68-15225
J.D. Fokker, H. Zantema, S.D. Swierstra (1991). "Iteratie en invariatie", Programmeren en Correctheid. Academic Service. ISBN 90-6233-681-7.
Weisstein, Eric W. "Invariant". MathWorld.
Popov, V.L. (2001) [1994], "Invariant", Encyclopedia of Mathematics, EMS Press

External links

"Applet: Visual Invariants in Sorting Algorithms" by William Braynen in 1997

[1] "Invariant Definition (Illustrated Mathematics Dictionary)". www.mathsisfun.com. Retrieved 2019-12-05.

[:1-2] Weisstein, Eric W. "Invariant". mathworld.wolfram.com. Retrieved 2019-12-05.

[:2-3] "Invariant – Encyclopedia of Mathematics". www.encyclopediaofmath.org. Retrieved 2019-12-05.

[4] Fraleigh (1976, pp. 166–167)

[5] Kay (1969, pp. 219)

[6] Differential Invariants for Differential Equations by André Platzer

[7] Hofstadter, Douglas R. (1999) [1979], Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, ISBN 0-465-02656-7 Here: Chapter I.

[Simon-8] Barry Simon. Representations of Finite and Compact Groups. American Mathematical Soc. p. 16. ISBN 978-0-8218-7196-6.

[9] Judith Cederberg (1989). A Course in Modern Geometries. Springer. p. 174. ISBN 978-1-4757-3831-5.

[10] Fraleigh (1976, p. 103)

[11] Herstein (1964, p. 42)

[12] McCoy (1968, p. 183)

[13] Bouajjani, A.; Drǎgoi, C.; Enea, C.; Rezine, A.; Sighireanu, M. (2010). "Invariant Synthesis for Programs Manipulating Lists with Unbounded Data" (PDF). Proc. CAV. doi:10.1007/978-3-642-14295-6_8.

[14] Hoare, C. A. R. (October 1969). "An axiomatic basis for computer programming" (PDF). Communications of the ACM. 12 (10): 576–580. doi:10.1145/363235.363259. S2CID 207726175. Archived from the original (PDF) on 2016-03-04.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]