1 + 2 + 4 + 8 + ⋯

Original article: w:1 + 2 + 4 + 8 + ⋯

The first four partial sums of 1 + 2 + 4 + 8 + ⋯.

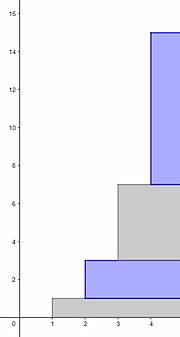
수학(mathematics)에서, 1 + 2 + 4 + 8 + ⋯은 그것의 항이 연속적인 이의 거듭제곱(powers of two)인 무한 급수(infinite series)입니다. 기하 급수(geometric series)로서, 그것은 첫 번째 항, 1과 공통 비율(common ratio), 2에 의해 특성화됩니다. 실수(real number)의 급수로서, 그것은 무한대(infinity)로 발산(diverges)하므로, 보통의 의미에서 그것은 합을 가지지 않습니다. 훨씬 더 넓은 의미에서, 그 급수는 ∞ 이외의 또 다른 값, 즉 2-진수 메트릭을 사용하는 급수의 극한인 –1과 결합됩니다.

Summation

$1+2+4+8+\cdots$의 부분 합은 $1,3,7,15,\ldots$입니다; 이것들이 무한대로 발산하기 때문에 그 급수도 마찬가지입니다. $$2^{0}+2^{1}+\cdots +2^{k}=2^{k+1}-1$$

그러므로, 임의의 전체적으로 정규 합계 방법(totally regular summation method)은 체사로 합(Cesàro sum)과 아벨 합(Abel sum)을 포함하여 무한대의 합을 제공합니다. 다른 한편으로, $1+2+4+8+\cdots$를 −1의 유한 값으로 합하는 적어도 하나의 일반적으로 유용한 방법이 있습니다. 결합된 거듭제곱 급수(power series)는 $$f(x)=1+2x+4x^{2}+8x^{3}+\cdots +2^{n}{}x^{n}+\cdots ={\frac {1}{1-2x}}$$ 오직 ${\frac {1}{2}}$의 0 주위로 수렴의 반지름)radius of convergence)을 가지므로 그것은 $x=1$에서 수렴하지 않습니다. 그럼에도 불구하고, 그렇게-정의된 함수 $f$는 삭제된 점 $x={\frac {1}{2}}$을 갖는 복소 평면(complex plane)에 대한 고유한 해석적 연속성(analytic continuation)을 가지고, 그것은 같은 규칙 $f(x)={\frac {1}{1-2x}}$에 의해 제공됩니다. $f(1)=-1$이기 때문에, 원래 급수 $1+2+4+8+\cdots$는 −1 합-가능 (E)이라고 말해지고, (E)은 그 급수의 (E) 합입니다. (표기법은 발산 급수에 대한 레온하르트 오일러(Leonhard Euler)의 접근 방식에 대한 참조에서 고드프리 해럴드 하디(G. H. Hardy)에 기인합니다.

거의 동일한 접근 방식 (오일러 자신에 의해 취해진 방식)은 그것의 계수가 모두 1인 거듭제곱 급수를 고려하는 것입니다. 즉, $$1+y+y^{2}+y^{3}+\cdots ={\frac {1}{1-y}}$$

그리고 $y=2$를 대입합니다. 이들 두 급수는 치환 $y=2x$에 의해 관련됩니다.

(E) 합계가 유한 값을 $1+2+4+8+\cdots$에 할당한다는 사실은 일반적인 방법이 전체적으로 정규가 아님을 보여줍니다. 다른 한편으로, 그것은 안정성과 선형성을 포함하여 합계 방법에 대해 몇 가지 다른 바람직한 속성을 가지고 있습니다. 이들 후자의 두 공리는 실제로 그 합을 −1로 강제하는데, 왜냐하면 그것들은 다음 조작을 유효하게 만들기 때문입니다:

${\begin{array}{rcl}s&=&\displaystyle 1+2+4+8+16+\cdots \\&=&\displaystyle 1+2(1+2+4+8+\cdots )\\&=&\displaystyle 1+2s\end{array}}$

유용한 의미에서, $s=\infty$는 방정식 $s=1+2s$의 근입니다. (예를 들어, $\infty$는 리만 구(Riemann sphere) 위에 뫼비우스 변환(Möbius transformation) $z\mapsto 1+2z$의 두 고정된 점(fixed point) 중 하나입니다). 만약 일부 합계 방법이 $s$에 대해 보통의 숫자로 반환하는 것으로 알려져 있으면; 즉, $\infty$가 아니면, 그것은 쉽게 결정됩니다. 이 경우에서 $s$는 방정식의 양쪽 변에서 빼질 수 있으며, $0=1+s$을 산출하므로, $s=-1$입니다.

위의 조작은 충분하게 강력한 합계 절차의 문맥 외부에서 −1을 생성하기 위해 호출될 수 있습니다. 기본 수렴 개념을 포함하여 가장 잘 알려져 있고 직접적인 합 개념에 대해, 양의 항의 급수가 음의 값을 가질 수 있다는 것은 터무니없는 일입니다. 유사한 현상은 발산 기하 급수 $1-1+1-1+\cdots$ (그란디 급수(Grandi's series))에서 발생하며, 여기서 정수(integer)의 급수가 비-정수 합 ${\frac {1}{2}}$를 가지는 것으로 보입니다. 이들 예제는 $0.111\ldots$과 가장 주목할만한 $0.999\ldots$와 같이 그러한 반복하는 십진(recurring decimal)에 의해 암시되는 급수에 유사한 논증을 적용하는 것에서 잠재적인 위험을 묘사합니다. 그 논증은 궁극적으로 이들 수렴 급수에 대해 정당화되며, $0.111\ldots ={\frac {1}{9}}$와 $0.999\ldots =1$임을 의미하지만, 놓여있는 증명(proof)은 끝없는 합의 해석에 대해 신중한 생각을 요구합니다.

이 급수를 실수와 다른 숫자 시스템, 즉, 2-진수 숫자에서 수렴하는 것으로 볼 수도 있습니다. 2-진수 숫자의 급수로서, 이 급수는 해석적 연속에 의해 위에서 도출된 것과 같은 같은 합, −1로 수렴합니다.

See also

• 1 − 1 + 2 − 6 + 24 − 120 + · · ·
• Grandi's series
• 1 + 1 + 1 + 1 + · · ·
• 1 − 2 + 3 − 4 + · · ·
• 1 + 2 + 3 + 4 + · · ·
• 1 − 2 + 4 − 8 + ⋯
• Two's complement, a data convention for representing negative numbers where −1 is represented as if it were 1 + 2 + 4 + ⋯ + 2ⁿ⁻¹.