Circumscribed circle

Original article: w:Circumscribed circle

This article is about circumscribed circles in geometry. For the use of circumscribed in biological classification, see Circumscription (taxonomy).

Circumscribed circle, C, and circumcenter, O, of a cyclic polygon, P

기하학(geometry)에서, 다각형(polygon)의 둘레-접하는 원(circumscribed circle) 또는 둘레-원(circumcircle)은 다각형의 모든 꼭짓점(vertices)을 통과하는 원(circle)입니다. 이 원의 중심은 둘레-중심(circumcenter)이라고 불리고 그것의 반지름은 둘레-반지름(circumradius)라고 불립니다.

모든 각 다각형에 둘레-접하는 원을 가지는 것은 아닙니다. 둘레원을 가지는 다각형은 순환 다각형(cyclic polygon), 또는 때때로 일치순환 다각형(concyclic polygon)이라고 불리는데 왜냐하면 그것의 꼭짓점이 일치순환(concyclic)이기 때문입니다. 모든 삼각형(triangle), 모든 정규(regular) 단순 다각형(simple polygon), 모든 직사각형(rectangle), 모든 이등변 사다리꼴(isosceles trapezoid), 및 모든 직각 연꼴(right kite)은 순환적입니다.

관련된 개념은 최소 경계하는 원(minimum bounding circle) 중 하나이며, 만약 그 원의 중심이 다각형 내에있으면, 그것 안에 다각형을 완전히 포함하는 가장 작은 원입니다. 모든 각 다각형이 고유한 최소 경계하는 원을 가지며, 이것은 선형 시간(linear time) 알고리듬에 의해 구성될 수 있습니다. 심지어 다각형이 둘레-접하는 원을 가지더라고, 그것의 최소 경계하는 원과 다를 수 있습니다. 예를 들어, 둔각 삼각형(obtuse triangle)에 대해, 최소 경계하는 원은 지름으로 가장 긴 변을 가지고 반대쪽 꼭짓점을 통과하지 않습니다.

Triangles

모든 삼각형이 순환적입니다; 즉, 모든 각 삼각형은 둘레-접하는 원을 가집니다.

Straightedge and compass construction

Construction of the circumcircle (red) and the circumcenter Q (red dot)

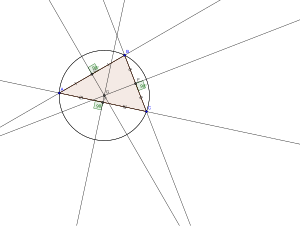
삼각형의 둘레-중심은 셋의 수직 이등분선(perpendicular bisectors) 중 임의의 둘을 그림으로써 구성될(constructed) 수 있습니다. 셋의 비-공선 점에 대해, 이들 두 직선은 평행일 수 없고, 둘레-중심은 그것들이 교차하는 점입니다. 이등분선 위의 모든 점은 그것이 이등분하는 두 점에서 같은-거리에 있으며, 이 점은, 이등분선 둘 다 위에, 모든 셋의 삼각형 꼭짓점에서 같은-거리에 있음으로부터 따릅니다. 둘레-반지름은 그것에서 셋의 꼭짓점 중 임의의 하나까지의 거리입니다.

Alternative construction

Alternative construction of the circumcenter (intersection of broken lines)

둘레-중심을 결정하는 대안적인 방법은 꼭짓점 중 하나에서 출발하는 임의의 두 개의 직선을 공통 변과 각도에서 각각 그리는 것이며, 공통 출발의 각도는 90°에서 반대 꼭짓점의 각도를 뺀 값입니다. (반대 각도가 둔각인 경우에서, 음의 각도로 직선을 그리는 것은 삼각형 밖으로 나가는 것을 의미합니다.)

연안의 항법(coastal navigation)에서, 삼각형의 둘레원은 때때로 나침반(compass)이 유용하지 없을 때 육분의(sextant)를 사용하여 위치 선(position line)을 얻는 방법으로 사용됩니다. 두 랜드마크 사이의 수평 각도는 관찰자가 놓여있는 둘레원을 정의합니다.

Circumcircle equations

Cartesian coordinates

유클리드 평면(Euclidean plane)에서, 내접된 삼각형의 꼭짓점의 데카르트 좌표(Cartesian coordinates)의 관점에서 둘레원의 방정식을 명시적으로 제공하는 것이 가능합니다. 다음이 점 A, B, 및 C의 좌표임을 가정합니다:

${\begin{aligned}\mathbf {A} &=(A_{x},A_{y})\\\mathbf {B} &=(B_{x},B_{y})\\\mathbf {C} &=(C_{x},C_{y})\end{aligned}}$

둘레원은 그런-다음 다음 방정식을 만족시키는 데카르트 평면에서 점 v = (v_x,v_y)의 자취입니다:

${\begin{aligned}|\mathbf {v} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {A} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {B} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {C} -\mathbf {u} |^{2}&=r^{2}\end{aligned}}$

여기서 점 A, B, C, 및 v는 그 원의 공통 중심 u에서 모두 같은 거리 r임을 보장합니다. 극화 항등식(polarization identity)을 사용하여, 이들 방정식은 다음 행렬(matrix)이 비-영 커널(kernel)을 가진다는 조건으로 줄어듭니다:

${\begin{bmatrix}|\mathbf {v} |^{2}&-2v_{x}&-2v_{y}&-1\\|\mathbf {A} |^{2}&-2A_{x}&-2A_{y}&-1\\|\mathbf {B} |^{2}&-2B_{x}&-2B_{y}&-1\\|\mathbf {C} |^{2}&-2C_{x}&-2C_{y}&-1\end{bmatrix}}$

따라서 둘레원은 이 행렬의 행렬식(determinant)의 영들의 자취(locus)로 대안적으로 묘사될 수 있습니다:

$\det {\begin{bmatrix}|\mathbf {v} |^{2}&v_{x}&v_{y}&1\\|\mathbf {A} |^{2}&A_{x}&A_{y}&1\\|\mathbf {B} |^{2}&B_{x}&B_{y}&1\\|\mathbf {C} |^{2}&C_{x}&C_{y}&1\end{bmatrix}}=0.$

여인수 전개(cofactor expansion)를 사용하여, 다음을 놓습니다:

${\begin{aligned}S_{x}&={\frac {1}{2}}\det {\begin{bmatrix}|\mathbf {A} |^{2}&A_{y}&1\\|\mathbf {B} |^{2}&B_{y}&1\\|\mathbf {C} |^{2}&C_{y}&1\end{bmatrix}},\\[5pt]S_{y}&={\frac {1}{2}}\det {\begin{bmatrix}A_{x}&|\mathbf {A} |^{2}&1\\B_{x}&|\mathbf {B} |^{2}&1\\C_{x}&|\mathbf {C} |^{2}&1\end{bmatrix}},\\[5pt]a&=\det {\begin{bmatrix}A_{x}&A_{y}&1\\B_{x}&B_{y}&1\\C_{x}&C_{y}&1\end{bmatrix}},\\[5pt]b&=\det {\begin{bmatrix}A_{x}&A_{y}&|\mathbf {A} |^{2}\\B_{x}&B_{y}&|\mathbf {B} |^{2}\\C_{x}&C_{y}&|\mathbf {C} |^{2}\end{bmatrix}}\end{aligned}}$

우리는 그런-다음 a|v|² − 2Sv − b = 0을 가지고, 셋의 점은 직선 안에 있지 않음을 가정하여 (그렇지 않으면 둘레원은 역시 무한대에서 S를 갖는 일반화된 원으로 보일 수 있는 해당 직선입니다), |v − S/a|² = b/a + |S|²/a², 둘레중심 S/a와 둘레반지름 √b/a + |S|²/a²을 제공합니다. 유사한 접근 방법은 사면체(tetrahedron)의 둘레-구(circumsphere)의 방정식을 추론하는 것을 허용합니다.

Parametric equation

원을 포함하는 평면에 수직(perpendicular)인 단위 벡터(unit vector)는 다음에 의해 제공됩니다:

${\widehat {n}}={\frac {(P_{2}-P_{1})\times (P_{3}-P_{1})}{|(P_{2}-P_{1})\times (P_{3}-P_{1})|}}.$

따라서, 반지름, r, 중심, P_c, 원 위의 한 점, P₀ 및 원을 포함하는 평면의 단위 법선, ${\textstyle {\widehat {n}}}$이 주어지면, 점 P₀로 시작하고 $\scriptstyle {\widehat {n}}$에 대한 양적으로 방향화된 (즉, 오른-손(right-handed)) 의미에서 진행하는 원의 하나의 매개변수 방정식은 다음입니다:

$\mathrm {R} (s)=\mathrm {P_{c}} +\cos \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)(P_{0}-P_{c})+\sin \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)\left[{\widehat {n}}\times (P_{0}-P_{c})\right].$

Trilinear and barycentric coordinates

삼-선형 좌표(trilinear coordinates) x : y : z에서 둘레원에 대한 방정식은 다음입니다: a/x + b/y + c/z = 0. 질량-중심 좌표(barycentric coordinates) x : y : z에서 둘레원에 대한 방정식은 다음입니다: a²/x + b²/y + c²/z = 0.

둘레원의 등각형 켤레(isogonal conjugate)는, ax + by + cz = 0에 의해 삼-선형 좌표(trilinear coordinates) 및 x + y + z = 0에 의해 질량-중심 좌표에서 주어진, 무한대에서 직선입니다.

Higher dimensions

추가적으로, d 차원에서 삽입된 삼각형의 둘레원은 일반화된 방법을 사용하여 찾아질 수 있습니다. A, B, C를 삼각형의 꼭짓점을 형성하는 d-차원 점이라고 놓습니다. 우리는 C를 원점에 배치하기 위해 시스템을 전치함으로써 시작합니다:

${\begin{aligned}\mathbf {a} &=\mathbf {A} -\mathbf {C} ,\\\mathbf {b} &=\mathbf {B} -\mathbf {C} .\end{aligned}}$

둘레-반지름, r은 그런-다음 다음입니다:

$r={\frac {\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left\|\mathbf {a} -\mathbf {b} \right\|}{2\left\|\mathbf {a} \times \mathbf {b} \right\|}}={\frac {\left\|\mathbf {a} -\mathbf {b} \right\|}{2\sin \theta }}={\frac {\left\|\mathbf {A} -\mathbf {B} \right\|}{2\sin \theta }},$

여기서 θ는 a와 b 사이의 내부 각도입니다. 둘레중심, p₀는 다음에 의해 제공됩니다:

$p_{0}={\frac {(\left\|\mathbf {a} \right\|^{2}\mathbf {b} -\left\|\mathbf {b} \right\|^{2}\mathbf {a} )\times (\mathbf {a} \times \mathbf {b} )}{2\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}}}+\mathbf {C} .$

이 공식은 교차 곱이 다른 차원에서 정의되지 않았기 때문에 오직 삼차원에서 작동하지만, 그것은 교차 곱을 다음 항등식으로 대체함으로써 다른 차원으로 일반화될 수 있습니다:

${\begin{aligned}(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} &=(\mathbf {a} \cdot \mathbf {c} )\mathbf {b} -(\mathbf {b} \cdot \mathbf {c} )\mathbf {a} ,\\\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )&=(\mathbf {a} \cdot \mathbf {c} )\mathbf {b} -(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} ,\\\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}&=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.\end{aligned}}$

Circumcenter coordinates

Cartesian coordinates

둘레중심 $U=\left(U_{x},U_{y}\right)$의 데카르트 좌표(Cartesian coordinates)는 다음입니다:

${\begin{aligned}U_{x}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_{y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})\right]\\[5pt]U_{y}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})\right]\end{aligned}}$

여기서

$D=2\left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})\right].\,$

일반성의 손실 없이, 이것은 꼿짓점 A를 데카르트 좌표 시스템의 원점으로 평행이동한 후, 즉, A′ = A − A = (A′_x,A′_y) = (0,0)일 때, 단순화된 형식으로 표현될 수 있습니다. 이 경우에서, 꼭짓점 B′ = B − A 및 C′ = C − A의 좌표는 꼭짓점 A′에서 이들 꼭짓점까지의 벡터를 나타냅니다. 이 자명한 평행이동이 모든 삼각형과 삼각형 A′B′C′의 둘레중심에 대해 다음처럼 가능하다는 것을 관찰하십시오:

${\begin{aligned}U'_{x}&={\frac {1}{D'}}\left[C'_{y}({B'_{x}}^{2}+{B'_{y}}^{2})-B'_{y}({C'_{x}}^{2}+{C'_{y}}^{2})\right],\\[5pt]U'_{y}&={\frac {1}{D'}}\left[B'_{x}({C'_{x}}^{2}+{C'_{y}}^{2})-C'_{x}({B'_{x}}^{2}+{B'_{y}}^{2})\right]\end{aligned}}$

여기서

$D'=2(B'_{x}C'_{y}-B'_{y}C'_{x}).\,$

꼭짓점 A를 원점으로 평행이동으로 인해, 둘레-반지름 r은 다음처럼 계산될 수 있습니다:

$r=\|U'\|={\sqrt {{U'_{x}}^{2}+{U'_{y}}^{2}}}$

그리고 ABC의 실제 둘레중심은 다음처럼 계산될 수 있습니다:

$U=U'+A$

Trilinear coordinates

둘레중심은 다음 삼-선형 좌표(trilinear coordinates)를 가집니다:

cos α : cos β : cos γ

여기서 α, β, γ는 삼각형의 각도입니다.

변 길이 a, b, c의 관점에서, 삼-선형은 다음입니다:

$a\left(b^{2}+c^{2}-a^{2}\right):b\left(c^{2}+a^{2}-b^{2}\right):c\left(a^{2}+b^{2}-c^{2}\right).$

Barycentric coordinates

둘레중심은 다음 질량-중심 좌표(barycentric coordinates)를 가집니다:

$a^{2}\left(b^{2}+c^{2}-a^{2}\right):\;b^{2}\left(c^{2}+a^{2}-b^{2}\right):\;c^{2}\left(a^{2}+b^{2}-c^{2}\right),\,$

여기서 a, b, c는 삼각형의 가장자리 길이 (각각, BC, CA, AB)입니다.

삼각형의 각도 $\alpha ,\beta ,\gamma$의 관점에서, 둘레중심의 질량-중심 좌표는 다음입니다:

$\sin 2\alpha :\sin 2\beta :\sin 2\gamma .$

Circumcenter vector

임의의 점의 데카르트 좌표는 그것들의 꼭짓점의 가중된 평균이고, 가중은 합해서 단위로 정규화된 점의 질량-중심 좌표이므로, 둘레중심 벡터는 다음처럼 쓸 수 있습니다:

$U={\frac {a^{2}\left(b^{2}+c^{2}-a^{2}\right)A+b^{2}\left(c^{2}+a^{2}-b^{2}\right)B+c^{2}\left(a^{2}+b^{2}-c^{2}\right)C}{a^{2}\left(b^{2}+c^{2}-a^{2}\right)+b^{2}\left(c^{2}+a^{2}-b^{2}\right)+c^{2}\left(a^{2}+b^{2}-c^{2}\right)}}.$

여기서 U는 둘레중심의 벡터이고 A, B, C는 꼭짓점 벡터입니다. 제수는 여기서 16S ²와 같고 S는 삼각형의 넓이입니다. 앞서 언급했듯이,

${\begin{aligned}\mathbf {a} &=\mathbf {A} -\mathbf {C} ,\\\mathbf {b} &=\mathbf {B} -\mathbf {C} .\end{aligned}}$

Cartesian coordinates from cross- and dot-products

유클리드 공간(Euclidean space)에서, 임의의 주어진 셋의 같은 직선 위에 있지 않은 점 P₁, P₂, 및 P₃을 통과하는 고유한 원이 있습니다. 데카르트 좌표(Cartesian coordinates)를 사용하여 이들 점을 공간 벡터(spatial vector)로 나타내기 위해, 점 곱(dot product)과 교차 곱(cross product)을 원의 반지름과 중심을 계산하기 위해 사용하는 것이 가능합니다. 다음으로 놓습니다:

$\mathrm {P_{1}} ={\begin{bmatrix}x_{1}\\y_{1}\\z_{1}\end{bmatrix}},\mathrm {P_{2}} ={\begin{bmatrix}x_{2}\\y_{2}\\z_{2}\end{bmatrix}},\mathrm {P_{3}} ={\begin{bmatrix}x_{3}\\y_{3}\\z_{3}\end{bmatrix}}$

그런-다음 원의 반지름은 다음에 의해 제공됩니다:

$\mathrm {r} ={\frac {\left|P_{1}-P_{2}\right|\left|P_{2}-P_{3}\right|\left|P_{3}-P_{1}\right|}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|}}$

원의 중심은 선형 조합(linear combination)에 의해 제공됩니다:

$\mathrm {P_{c}} =\alpha \,P_{1}+\beta \,P_{2}+\gamma \,P_{3}$

여기서

${\begin{aligned}\alpha ={\frac {\left|P_{2}-P_{3}\right|^{2}\left(P_{1}-P_{2}\right)\cdot \left(P_{1}-P_{3}\right)}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|^{2}}}\\\beta ={\frac {\left|P_{1}-P_{3}\right|^{2}\left(P_{2}-P_{1}\right)\cdot \left(P_{2}-P_{3}\right)}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|^{2}}}\\\gamma ={\frac {\left|P_{1}-P_{2}\right|^{2}\left(P_{3}-P_{1}\right)\cdot \left(P_{3}-P_{2}\right)}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|^{2}}}\end{aligned}}$

Location relative to the triangle

둘레중심의 위치는 삼각형의 유형에 따라 다릅니다:

• 예각 삼각형 (모든 각도가 직각보다 작음)에 대해, 둘레중심은 항상 삼각형의 내부에 놓입니다.
• 직각 삼각형에 대해, 둘레중심은 항상 빗변(hypotenuse)의 중간점에 놓입니다. 이것은 탈레스의 정리(Thales' theorem)의 한 형식입니다.
• 둔각 삼각형 (직각 보다 더 큰 하나의 각도를 갖는 삼각형)에 대해, 둘레중심은 항상 삼각형의 밖에 놓입니다.

The circumcenter of an acute triangle is inside the triangle

The circumcenter of a right triangle is at the midpoint of the hypotenuse

The circumcenter of an obtuse triangle is outside the triangle

이들 위치적 특징은 둘레중심에 대해 위에 제공된 삼-선형 또는 질량-중심 좌표를 고려함으로써 보일 수 있습니다: 모든 세 좌표는 임의의 내부 점에 대해 양수이고, 적어도 하나의 좌표는 임의의 외부 점에 대해 음수이고, 하나의 좌표는 영이고 둘이 삼각형의 한 변에 있는 비-꼭짓점에 대해 양수입니다.

Angles

둘레에-새겨진 원이 삼각형의 변과 형성하는 각도는 변이 서로 만나는 각도와 일치합니다. 변 반대쪽 각도 α는 원과 두 번 만납니다: 각 끝에서 한 번씩; 각각의 경우에서 각도 α로 만납니다 (다른 두 각도에 대해 유사합니다). 이것은 접선과 현 사이의 각도가 교대 선분에서 각도와 같다는 교대 선분 정리(alternate segment theorem) 때문입니다.

Triangle centers on the circumcircle of triangle ABC

이 섹션에서, 꼭짓점 각도는 A, B, C로 레이블이 지정되고 모든 좌표는 삼-선형 좌표(trilinear coordinates)입니다:

• 슈타이너 점(Steiner point) = bc / (b² − c²) : ca / (c² − a²) : ab / (a² − b²) = 둘레원과 슈타이너 타원의 교차점의 꼭짓점이 아닌 점. (슈타이너 타원(Steiner ellipse)은, 중심 = 도형중심 (ABC)과 함께, A, B, 및 C를 통과하는 최소 넓이의 타원입니다. 이 타원에 대한 방정식은 1/(ax) + 1/(by) + 1/(cz) = 0입니다.)
• 탈히 점(Tarry point) = sec (A + ω) : sec (B + ω) : sec (C + ω) = 슈타이너 점의 대척점
• 키페르트 포물선(Kiepert parabola)의 초점 = csc (B − C) : csc (C − A) : csc (A − B).

Other properties

둘레원의 지름(diameter)은, 둘레지름(circumdiameter)이라고 불리고 둘레반지름(circumradius)의 두 배와 같으며, 삼각형의 임의의 변의 길이를 반대쪽 각도(angle)의 사인(sine)으로 나눈 것으로 계산될 수 있습니다:

${\text{diameter}}={\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}.$

사인의 법칙(law of sines)의 결과로써, 어떤 변과 반대쪽 각도를 취하는지는 중요하지 않습니다: 그 결과는 같을 것입니다.

둘레원의 지름은 역시 다음으로 표현될 수 있습니다:

${\begin{aligned}{\text{diameter}}&{}={\frac {abc}{2\cdot {\text{area}}}}={\frac {|AB||BC||CA|}{2|\Delta ABC|}}\\[5pt]&{}={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\[5pt]&{}={\frac {2abc}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}\end{aligned}}$

여기서 a, b, c는 삼각형의 변의 길이이고 s = (a + b + c)/2는 반둘레입니다. 위의 표현 ${\sqrt {\scriptstyle {s(s-a)(s-b)(s-c)}}}$은 헤론의 공식(Heron's formula)에 의한 삼각형의 넓이입니다. 둘레원의 지름에 대해 삼각 표현은 다음을 포함합니다:

${\text{diameter}}={\sqrt {\frac {2\cdot {\text{area}}}{\sin A\sin B\sin C}}}.$

삼각형의 아홉-점 원(nine-point circle)은 둘레원의 지름의 절반입니다.

임의의 주어진 삼각형에서, 둘레원은 항상 도형-중심(centroid)과 직교-중심(orthocenter)과 같은 직선 위에 놓입니다. 그것들의 모두를 통과하는 직선은 오일러 직선(Euler line)으로 알려져 있습니다.

둘레중심의 등각형 켤레(isogonal conjugate)는 직교중심(orthocenter)입니다.

세 점의 유용한 최소 경계하는 원(minimum bounding circle)은 둘레원에 의해 (여기서 세 점은 최소 경계하는 원 위에 있음) 또는 삼각형의 가장 긴 변의 두 점에 의해 (여기서 두 점은 원의 지름을 정의함) 정의됩니다. 최소 경계 원과 둘레 원을 혼동하는 것이 공통적입니다.

셋의 같은 직선 위의 점(collinear points)의 둘레원은 세 점이 놓인 직선이며, 종종 무한 반지름의 원(circle of infinite radius)으로 참조됩니다. 거의 같은 직선 위의 점은 종종 둘레원의 계산에서 수치적 불안정성(numerical instability)으로 이어집니다.

삼각형의 둘레원은 점들의 집합(set)의 델로네 삼각분할(Delaunay triangulation)과 밀접한 관계를 가집니다.

기하학에서 오일러의 정리(Euler's theorem in geometry)에 의해, 둘레원 O와 내-중심(incenter) I 사이의 거리는 다음입니다:

$OI={\sqrt {R(R-2r)}},$

여기서 r은 내-원 반지름이고 R은 둘레원 반지름입니다; 따라서 둘레반지름은 적어도 내반지름의 두 배이며 ((오일러의 삼각형 부등식(Euler's triangle inequality)), 이때 상등은 오직 같은-변(equilateral) 경우입니다.

둘레중심 O와 직교-중심(orthocenter) H 사이의 거리는 다음입니다:

$OH={\sqrt {R^{2}-8R^{2}\cos A\cos B\cos C}}={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}.$

도형-중심(centroid) G와 아홉-점 중심(nine-point center) N에 대해 우리는 다음을 가집니다:

${\begin{aligned}IG&<IO,\\2IN&<IO,\\OI^{2}&=2R\cdot IN.\end{aligned}}$

변 a, b, 및 c를 갖는 삼각형의 내원 반지름과 둘레원 반지름의 곱은 다음입니다:

$rR={\frac {abc}{2(a+b+c)}}.$

둘레반지름 R, 변 a, b, c, 및 중앙선(medians) m_a, m_b, 및 m_c와 함께, 우리는 다음을 가집니다:

${\begin{aligned}3{\sqrt {3}}R&\geq a+b+c\\[5pt]9R^{2}&\geq a^{2}+b^{2}+c^{2}\\[5pt]{\frac {27}{4}}R^{2}&\geq m_{a}^{2}+m_{b}^{2}+m_{c}^{2}.\end{aligned}}$

만약 중앙선 m, 고도 h, 및 내부 이등분선 t 모두가 둘레반지름 R을 갖는 삼각형의 같은 꼭짓점에서 나오면, 다음입니다:

$4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).$

카르노의 정리(Carnot's theorem)는 둘레중심에서 셋의 변까지의 거리의 합이 둘레반지름과 내-반지름(inradius)의 합과 같음을 말합니다. 여기서 선분의 길이가 음수로 고려되는 것과 선분이 전적으로 삼각형 밖에 놓이는 것은 필요충분 조건입니다.

만약 삼각형이 그것의 둘레원과 내원(incircle)으로 둘의 특정 원을 가지면, 둘레원 위의 임의의 점을 꼭짓점으로 갖는 같은 둘레원과 내원을 갖는 무한한 숫자의 다른 삼각형이 존재합니다 (이것이 퐁슬레의 포리즘(Poncelet's porism)의 n = 3 경우입니다). 그러한 삼각형이 존재하기 위한 필요충분 조건은 위의 상등 $OI={\sqrt {R(R-2r)}}$입니다.

Cyclic quadrilaterals

Cyclic quadrilaterals

Main article: Cyclic quadrilateral

둘레-접해질 수 있는 사변형은 반대편 각도가 보충 각도(supplementary angles) (합해서 180° 또는 π 라디안)라는 사실을 포함하여 특정 속성을 가집니다.

Cyclic n-gons

홀수의 변을 갖는 순환 다각형에 대해, 모든 각도가 같은 것과 다각형이 정규인 것은 필요충분 조건입니다. 짝수의 변을 갖는 순환 다각형은 모두 같은 각을 가지는 것과 교대 변이 같은 것 (즉, 변 1, 3, 5, ...이 같고, 변 2, 4, 6, ... 같음)은 것은 필요충분 조건입니다.

유리수(rational) 변과 넓이를 갖는 순환 오각형(pentagon)은 로빈스 오각형(Robbins pentagon)으로 알려져 있습니다; 모든 알려진 경우에서, 그것의 대각선은 역시 유리수 길이를 가집니다.

짝수 n을 갖는 임의의 순환 n-각형에서, 한 집합의 교대 각도 (첫 번째, 세 번째, 다섯 번째 등)의 합은 다른 집합의 교대 각도의 합과 같습니다. 이것은 n=4 경우에서 귀납법에 의해 입증될 수 있으며, 각 경우에서 한면을 셋의 더 많은 변으로 대체하고 이들 셋의 새로운 변을 기존 변과 함께 사변형을 형성하며 그 자체가 이 속성을 갖는다는 점에 주목하십시오; 후자 사변형의 교대 각도는 이전 n-각형의 교대 각도 합에 대한 덧셈을 나타냅니다.

하나의 n-각형을 원으로 내접시키게 놓고, 또 다른 n-각형을 첫 번째 n-각형의 꼭짓점에서 해당 원에 접하게(tangential) 놓습니다. 그런-다음 원 위의 임의의 점 P에서, P에서 첫 번째 n-각형의 변까지의 수직 거리의 곱은 P에서 두 번째 n-각형의 변까지의 수직 거리의 곱과 같습니다.

Point on the circumcircle

순환 n-각형이 단위 원 위에 꼭짓점 A₁ , ..., A_n을 가진다고 놓습니다. 그런-다음 작은 쪽의 호 A₁A_n 위에 임의의 점 M에 대해, M에서 꼭짓점까지의 거리는 다음을 만족시킵니다:

${\begin{cases}MA_{1}+MA_{3}+\cdots +MA_{n-2}+MA_{n}<n/{\sqrt {2}}&{\text{if }}n{\text{ is odd}};\\MA_{1}+MA_{3}+\cdots +MA_{n-3}+MA_{n-1}\leq n/{\sqrt {2}}&{\text{if }}n{\text{ is even}}.\end{cases}}$

정규 n-각형에 대해, 만약 $MA_{i}$가 둘레원 위의 임의의 점 $M$에서 꼭짓점 $A_{i}$까지의 거리이면, 다음입니다:

$3(MA_{1}^{2}+MA_{2}^{2}+...+MA_{n}^{2})^{2}=2n(MA_{1}^{4}+MA_{2}^{4}+...+MA_{n}^{4}).$

Polygon circumscribing constant

A sequence of circumscribed polygons and circles.

임의의 정규 다각형(regular polygon)은 순환적입니다. 단위 원, 그런-다음 각 변이 원에 접촉함을 만족하는 정규 삼각형을 둘레-접한다고 생각해 보십시오. 원을 둘레-접하고, 그런-다음 정사각형을 둘레-접하십시오. 다시 원을 둘레-접하고, 그런-다음 정규 5-각형을 둘레-접하고, 이런 식으로 계속합니다. 둘레-접된 원의 반지름은 소위 다각형 둘레-접하는 상수(polygon circumscribing constant)로 수렴합니다.

$\prod _{n=3}^{\infty }{\frac {1}{\cos \left({\frac {\pi }{n}}\right)}}=8.7000366\ldots .$

(OEIS에서 수열 A051762). 이 상수의 역수는 케플러–바우캄프 상수(Kepler–Bouwkamp constant)입니다.

See also

• Circumgon
• Circumscribed sphere
• Inscribed circle
• Japanese theorem for cyclic polygons
• Japanese theorem for cyclic quadrilaterals
• Jung's theorem, an inequality relating the diameter of a point set to the radius of its minimum bounding sphere
• Kosnita theorem
• Lester's theorem
• Tangential polygon
• Triangle center

External links

• Derivation of formula for radius of circumcircle of triangle at Mathalino.com
• Semi-regular angle-gons and side-gons: respective generalizations of rectangles and rhombi at Dynamic Geometry Sketches, interactive dynamic geometry sketch.

MathWorld

• Weisstein, Eric W. "Circumcircle". MathWorld.
• Weisstein, Eric W. "Cyclic Polygon". MathWorld.
• Weisstein, Eric W. "Steiner circumellipse". MathWorld.

Interactive

• Triangle circumcircle and circumcenter With interactive animation
• An interactive Java applet for the circumcenter