수학(mathematics) 에서, 급수(series) 는 숫자의 무한 수열(infinite sequence) 의 항들의 합(sum) 입니다. 보다 정확하게, 무한 수열
(
a
0
,
a
1
,
a
2
,
…
)
{\displaystyle (a_{0},a_{1},a_{2},\ldots )}
급수(series) S 를 정의합니다:
S
=
a
0
+
a
1
+
a
2
+
⋯
=
∑
k
=
0
∞
a
k
.
{\displaystyle S=a_{0}+a_{1}+a_{2}+\cdots =\sum _{k=0}^{\infty }a_{k}.}
n 부분 합(partial sum) S n n
S
n
=
∑
k
=
1
n
a
k
.
{\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}.}
(
S
1
,
S
2
,
S
3
,
…
)
{\displaystyle (S_{1},S_{2},S_{3},\dots )}
극한(limit) 으로 경향이면 수렴(convergent) 입니다 (또는 수렴합니다(converges) ); 그것은, 인덱스에 의해 주어진 순서에서
a
k
{\displaystyle a_{k}}
ε
{\displaystyle \varepsilon }
n
≥
N
{\displaystyle n\geq N}
정수(integer)
N
{\displaystyle N}
ℓ
{\displaystyle \ell }
|
S
n
−
ℓ
|
<
ε
.
{\displaystyle \left|S_{n}-\ell \right|<\varepsilon .}
만약 급수가 수렴하면, (필연적으로 고유한) 숫자
ℓ
{\displaystyle \ell }
급수의 합 이라고 불립니다.
다음 합 표기법은
∑
k
=
1
∞
a
k
{\displaystyle \sum _{k=1}^{\infty }a_{k}}
급수에 대해 사용되고, 만약 그것이 수렴하면, 합에 수렴합니다. 이 관례는 덧셈에 사용되는 것과 유사합니다: a + b a 와 b 를 더하는 연산a 와 b 의 합 이라고 불리는 이 덧셈 의 결과를 표시합니다.
수렴하지 않는 임의의 급수는 발산(divergent) 또는 발산하는 것이라고 말합니다.
Examples of convergent and divergent series 양의 정수(positive integers) 의 역수는 발산 급수(divergent series) (조화 급수(harmonic series) )를 생성합니다:
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
⋯
→
∞
.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .}
양의 정수의 역수의 부호를 교대하는 것은 수렴 급수 (교대 조화 급수(alternating harmonic series) )를 생성합니다:
1
1
−
1
2
+
1
3
−
1
4
+
1
5
−
⋯
=
ln
(
2
)
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-\cdots =\ln(2)}
소수의 역수는 발산 급수(divergent series) 를 생성합니다 (따라서 소수 집합은 "큰(large)" 것입니다; 소수의 역수의 합의 발산 을 참조하십시오):
1
2
+
1
3
+
1
5
+
1
7
+
1
11
+
1
13
+
⋯
→
∞
.
{\displaystyle {1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .}
삼각형 숫자(triangular number) 의 역수는 수렴 급수를 생성합니다:
1
1
+
1
3
+
1
6
+
1
10
+
1
15
+
1
21
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.}
팩토리얼(factorial) 의 역수는 수렴 급수를 생성합니다 (e 를 참조하십시오):
1
1
+
1
1
+
1
2
+
1
6
+
1
24
+
1
120
+
⋯
=
e
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.}
제곱 숫자(square number) 의 역수는 수렴 급수를 생성합니다 (바젤 문제(Basel problem) 를 참조하십시오):
1
1
+
1
4
+
1
9
+
1
16
+
1
25
+
1
36
+
⋯
=
π
2
6
.
{\displaystyle {1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.}
2의 거듭제곱(powers of 2) 의 역수는 수렴 급수를 생성합니다 (따라서 2의 거듭제곱의 집합은 ""작은(small)" 것입니다):
1
1
+
1
2
+
1
4
+
1
8
+
1
16
+
1
32
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.}
임의의 n>1의 거듭제곱(powers of any n>1) 의 역수는 수렴 급수를 생성합니다:
1
1
+
1
n
+
1
n
2
+
1
n
3
+
1
n
4
+
1
n
5
+
⋯
=
n
n
−
1
.
{\displaystyle {1 \over 1}+{1 \over n}+{1 \over n^{2}}+{1 \over n^{3}}+{1 \over n^{4}}+{1 \over n^{5}}+\cdots ={n \over n-1}.}
2의 거듭제곱(powers of 2) 의 역수의 부호를 교대하는 것은 역시 수렴 급수를 생성합니다:
1
1
−
1
2
+
1
4
−
1
8
+
1
16
−
1
32
+
⋯
=
2
3
.
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.}
임의의 n>1 거듭제곱의 역수의 부호를 교대하는 것은 수렴 급수를 생성합니다:
1
1
−
1
n
+
1
n
2
−
1
n
3
+
1
n
4
−
1
n
5
+
⋯
=
n
n
+
1
.
{\displaystyle {1 \over 1}-{1 \over n}+{1 \over n^{2}}-{1 \over n^{3}}+{1 \over n^{4}}-{1 \over n^{5}}+\cdots ={n \over n+1}.}
피보나치 숫자(Fibonacci number) 의 역수는 수렴 급수를 생성합니다 (ψ 를 참조하십시오):
1
1
+
1
1
+
1
2
+
1
3
+
1
5
+
1
8
+
⋯
=
ψ
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{8}}+\cdots =\psi .}
Convergence tests 급수가 수렴하는지 또는 발산(diverges) 하는지를 결정하는 여러 방법이 있습니다.
If the blue series,
Σ
b
n
{\displaystyle \Sigma b_{n}}
Σ
a
n
{\displaystyle \Sigma a_{n}}
Σ
a
n
{\displaystyle \Sigma a_{n}}
Σ
b
n
{\displaystyle \Sigma b_{n}}
비교 테스트(Comparison test)
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
{
b
n
}
{\displaystyle \left\{b_{n}\right\}}
n 에 대해,
0
≤
a
n
≤
b
n
{\displaystyle 0\leq \ a_{n}\leq \ b_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
어쨌든, 만약, 모든 n 에 대해,
0
≤
b
n
≤
a
n
{\displaystyle 0\leq \ b_{n}\leq \ a_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
비율 테스트(Ratio test) n 에 대해,
a
n
{\displaystyle a_{n}}
r
{\displaystyle r}
lim
n
→
∞
|
a
n
+
1
a
n
|
=
r
.
{\displaystyle \lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=r.}
만약 r < 1이면, 급수는 절대적으로 수렴입니다. 만약 r > 1r = 1
근 테스트(Root test) n 번째 근 테스트비-음수(non-negative) 라고 가정합니다. r 을 다음처럼 정의합니다:
r
=
lim sup
n
→
∞
|
a
n
|
n
,
{\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}
여기서 "lim sup"는 극한 상부(limit superior) 를 표시합니다 (아마도 ∞; 만약 극한이 존재하면 그것과 같은 갑입니다). 만약 r < 1이면, 급수는 수렴합니다. 만약 r > 1r = 1
비율 테스트와 근 테스트는 둘 다 기하학적 급수와의 비교를 기반으로 하고, 이들테면 그것들은 유사한 상황에서 작동합니다. 실제로, 만약 비율 테스트가 작동하면 (극한이 존재하고 1과 같지 않음을 의미), 근 테스트도 작동합니다; 그 전환은, 어쨌든, 참이 아닙니다. 근 테스트는 따라서 보다 일반적으로 적용-가능하지만, 실제적인 문제로 극한은 종종 공통적으로 보이는 급수의 유형을 위해 계산하는 것이 어렵습니다.
적분 테스트(Integral test)
f
(
n
)
=
a
n
{\displaystyle f(n)=a_{n}}
단조적으로 감소하는 함수(monotonically decreasing function) 라고 놓습니다. 만약 다음이면,
∫
1
∞
f
(
x
)
d
x
=
lim
t
→
∞
∫
1
t
f
(
x
)
d
x
<
∞
,
{\displaystyle \int _{1}^{\infty }f(x)\,dx=\lim _{t\to \infty }\int _{1}^{t}f(x)\,dx<\infty ,}
급수는 수렴합니다. 그러나 만약 적분이 발산하면, 급수도 마찬가지로 발산합니다.
극한 비교 테스트(Limit comparison test)
{
a
n
}
,
{
b
n
}
>
0
{\displaystyle \left\{a_{n}\right\},\left\{b_{n}\right\}>0}
lim
n
→
∞
a
n
b
n
{\displaystyle \lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
필요충분(iff) 조건입니다.
교대 급수 테스트(Alternating series test) 라이프니츠 기준 으로 알려져 있으며, 교대 급수 테스트(alternating series test) 는 형식
∑
n
=
1
∞
a
n
(
−
1
)
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}(-1)^{n}}
교대 급수(alternating series) 에 대해, 만약
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
감소(decreasing) 하고, 무한대에서 0의 극한을 가지면, 급수는 수렴한다고 말합니다.
코시 응집 테스트(Cauchy condensation test)
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
∑
k
=
1
∞
2
k
a
2
k
{\displaystyle \sum _{k=1}^{\infty }2^{k}a_{2^{k}}}
디리클레의 테스트(Dirichlet's test)
아벨의 테스트(Abel's test)
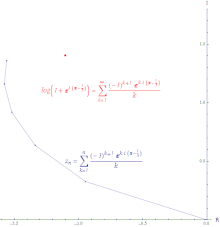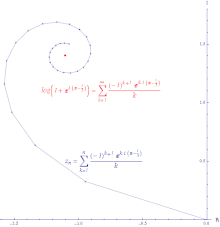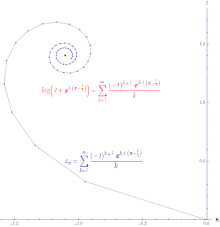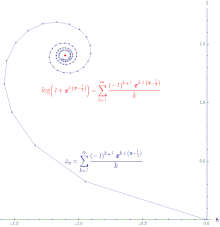
Conditional and absolute convergence Illustration of the conditional convergence of the power series of log(z +1) around 0 evaluated at z = exp((π − 1 ⁄3 i ). 임의의 수열
{
a
1
,
a
2
,
a
3
,
…
}
{\displaystyle \left\{a_{1},\ a_{2},\ a_{3},\dots \right\}}
n 에 대해
a
n
≤
|
a
n
|
{\displaystyle a_{n}\leq \left|a_{n}\right|}
∑
n
=
1
∞
a
n
≤
∑
n
=
1
∞
|
a
n
|
.
{\displaystyle \sum _{n=1}^{\infty }a_{n}\leq \sum _{n=1}^{\infty }\left|a_{n}\right|.}
이것은 만약
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right|}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
만약 급수
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right|}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
절대적으로 수렴(absolutely convergent) 입니다. 절대적으로 수렴하는 수열(convergent sequence) 은 부분 합에 대한 모든 증분을 함께 결합함으로써 생성된 직선의 길이가 유한하게 긴 수열입니다. 지수 함수(exponential function) 의 거듭제곱 급수는 어디에서나 절대적으로 수렴합니다.
만약 급수
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right|}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
조건적으로 수렴(conditionally convergent) 입니다. 조건적으로 수렴하는 급수의 부분 합을 연결함으로써 형성된 경로는 무한하게 깁니다. 로그(logarithm) 의 거듭제곱 급수는 조건적으로 수렴입니다.
리만 급수 정리(Riemann series theorem) 는 만약 급수가 조건적으로 수렴하면, 급수가 임의의 값으로 수렴하거나, 심지어 발산하는 그러한 방법에서 급수의 항을 재정렬할 수 있음을 말합니다.
Uniform convergence
{
f
1
,
f
2
,
f
3
,
…
}
{\displaystyle \left\{f_{1},\ f_{2},\ f_{3},\dots \right\}}
∑
n
=
1
∞
f
n
{\displaystyle \sum _{n=1}^{\infty }f_{n}}
{
s
n
}
{\displaystyle \{s_{n}\}}
f 에 균등하게 수렴한다고 말합니다:
s
n
(
x
)
=
∑
k
=
1
n
f
k
(
x
)
{\displaystyle s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)}
이것이 f 에 균등하게 수렴합니다.
바이어슈트라스 M-테스트(Weierstrass M-test) 라고 불리는 함수의 무한 급수에 대해 비교 테스트와 유사한 것이 있습니다.
Cauchy convergence criterion 코시 응집 테스트(Cauchy convergence criterion) 는 다음임을 말합니다: 다음 급수가
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
수렴하는 것과 부분 합(partial sum) 의 수열이 코시 수열(Cauchy sequence) 인 것은 필요충분(iff) 조건입니다.
이것은 모든 각
ε
>
0
{\displaystyle \varepsilon >0}
n
≥
m
≥
N
{\displaystyle n\geq m\geq N}
N
{\displaystyle N}
|
∑
k
=
m
n
a
k
|
<
ε
,
{\displaystyle \left|\sum _{k=m}^{n}a_{k}\right|<\varepsilon ,}
이것은 다음과 동등합니다:
lim
n
→
∞
m
→
∞
∑
k
=
n
n
+
m
a
k
=
0.
{\displaystyle \lim _{n\to \infty \atop m\to \infty }\sum _{k=n}^{n+m}a_{k}=0.}
See also External links



































![{\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}](https://dawoum.duckdns.org/api/rest_v1/media/math/render/svg/dd5eebb0f17b1155c0bea36edfdd50d6b9aa0f01)

















