Jump to content

Countable set

This is a fully translated article. Click here for more information.
From DawoumWiki, the free Mathematics self-learning
(Redirected from Countably infinite)
Original article: w:Countable set
"Countable" redirects here. For the linguistic concept, see Count noun. For the political media company, see Countable (app).
Not to be confused with (recursively) enumerable sets.

수학(mathematics)에서, 셀-수-있는 집합(countable set)은 자연수의 집합의 일부 부분집합(subset)과 같은 카디널리티(cardinality) (원소의 숫자(number))를 갖는 집합(set)입니다. 셀-수-있는 집합은 유한 집합(finite set) 또는 셀-수-있는 무한(countably infinite) 집합입니다. 유한 또는 무한 여부에 관계없이, 셀-수-있는 집합의 원소는–비록 세는 것이 결코 끝낼 수 없을지라도–항상 한 번에 하나씩 셀 수 있고 집합의 모든 각 원소는 고유한 자연수와 결합됩니다.

일부 저자는 셀-수-있는 집합을 단독으로 셀-수-있는 무한 을 의미하기 위해 사용합니다.[1] 이 모호함을 피하기 위해, 용어 많아야 셀-수-있는(at most countable)이 유한 집합이 포함될 때 사용할 수 있고, 그렇지 않으면 셀-수-있는 무한(countably infinite), 열거-가능한(enumerable),[2] 또는 번호-매길-수-있는(denumerable)[3]을 사용할 수 있습니다.

게오르크 칸토어(Georg Cantor)는 용어 셀-수-있는 집합(countable set)을 도입했으며, 셀-수-없는(uncountable) (즉, 열거할-수-없는(nonenumerable) 또는 번호-매길-수-없는(nondenumerable)[4]) 것인 집합과 셀-수-있는 것인 집합을 대조합니다. 오늘날, 셀-수-있는 집합은 이산 수학(discrete mathematics)이라고 불리는 수학의 가지의 토대를 형성합니다.

Definition

집합 S는 만약 S에서 자연수(natural numbers) N = {0, 1, 2, 3, ...}로의 단사 함수(injective function) f가 존재하면 셀-수-있는 것입니다.[citation needed][5]

만약 그러한 f가 역시 surjective (및 따라서 전단사)인 것을 발견할 수 있으면, S는 셀-수-있는 무한(countably infinite)이라고 불립니다.

달리 말해서, 집합이 만약 그것이 자연수의 집합, N과 일-대-일 대응(one-to-one correspondence)을 가지면 셀-수-있는 무한입니다. 이 경우에서, 집합의 카디널리티는 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \aleph_0} (알레프-널(aleph-null))–알레프 숫자의 수열에서 첫 번째–으로 표시됩니다.[6]

이 용어는 보편적이지 않습니다. 일부 저자는 셀-수-있는 것을 여기서 셀-수-있는 무한으로 불리는 것을 의미하기 위해 사용하고, 유한 집합을 포함하지 않습니다.

전단사(bijective) 함수 또는 전사(surjective) 함수의 관점에서 정의의 대안적인 (동등한) 공식이 역시 제공될 수 있습니다.[7] 역시 아래의 § Formal overview without details를 참조하십시오.

History

1874년에, 그의 첫 번째 집합 이론 기사에서, 칸토어는 실수(real number)의 집합이 셀-수-없는 것임을 입증하고, 따라서 모든 무한 집합이 셀-수-있는 것은 아니라는 것을 보여주었습니다.[8] 1878년에, 그는 카디널리티를 정의하고 비교하기 위해 일-대-일 대응을 사용했습니다.[9] 1883년에, 그는 무한 순서-숫자(ordinals)로 자연수를 확장하고, 순서-숫자의 집합을 서로 다른 무한 카디널리티를 갖는 집합의 무한대를 생성하기 위해 사용됩니다.[10]

Introduction

집합(set)은 원소의 모음이고, 다양한 방법으로 설명될 수 있습니다. 한 가지 방법은 단순히 그것의 원소의 모두를 나열하는 것입니다; 예를 들어, 정수 3, 4, 및 5로 구성된 집합은 {3, 4, 5}로 표시될 수 있습니다. 어쨌든, 이것은 오직 작은 집합에 효과적입니다; 더 큰 집합에 대해, 이것은 시간-소모적이고 오류의 경향이 있습니다. 모든 각 단일 원소를 나열하는 대신에, 때때로 생략부호가 만약 작성자가 독자가 누락된 것을 쉽게 추측할 수 있다고 믿으면 ("...")가 사용됩니다; 예를 들어 {1, 2, 3, ..., 100}은 아마도 1부터 100까지의 정수(integer)의 집합을 표시합니다. 심지어 이 경우에도, 어쨌든, 집합이 유한하기 때문에 모든 원소를 나열하는 것이 가능합니다.

일부 집합은 무한입니다; 이들 집합은 임의의 정수 n에 대해 n 원소보다 많은 것을 가집니다. 예를 들어, 자연수의 집합은, {0, 1, 2, 3, 4, 5, ...}로 표시되며, 무한하게 많은 원소를 가지고, 우리는 그것의 크기를 제공하기 위해 임의의 표준 숫자를 사용할 수 없습니다. 그럼에도 불구하고, 무한 집합은 잘-정의된 크기의 개념 (또는 보다 적절하게, 카디널리티, 집합에서 원소의 숫자에 대해 기술적 용어)을 가지고, 모든 무한 집합이 같은 카디널리티를 갖는 것은 아니라는 것을 밝혔습니다.

Bijective mapping from integer to even numbers

이것이 무엇을 의미하는지 이해하기 위해, 우리는 먼저 그것이 의미하지 않는 것을 조사합니다. 예를 들어, 무한하게 많은 홀수 정수, 무한하게 많은 짝수 정수, 및 (따라서) 전체적으로 무한하게 많은 정수가 있습니다. 어쨌든, 홀수 정수의 개수와 같은 것인, 짝수 정수의 개수가 역시 전체적으로 정수의 개수와 같다는 것이 밝혀졌습니다. 이것은 모든 정수에 대해, 구별되는 짝수 정수: ... −2→−4, −1→−2, 0→0, 1→2, 2→4, ...; 또는, 보다 일반적으로, n→2n가 있음을 만족하는 것을 배열할 수 있기 때문입니다 (그림을 참조하십시오). 우리가 한 것은 여기서 정수와 짝수를 일-대-일 대응 (또는 전단사(bijection))으로 배열하는 것이며, 이것은 각 집합의 각 원소가 나머지 다른 집합에서 단일 요소에 해당하는 것을 만족하는 두 집합 사이를 매핑하는 함수(function)입니다.

어쨌든, 모든 무한 집합이 같은 카디널리티를 갖는 것은 아닙니다. 예를 들어, 게오르크 칸토어(Georg Cantor) (그는 이 개념을 도입했음)는 실수가 자연수 (비-음의 정수)와 일-대-일 대응으로 놓을 수 없고, 따라서 실수의 집합이 자연수의 집합보다 더 큰 카디널리티를 가짐을 시연했습니다.

집합은 만약: (1) 그것이 유한함, 또는 (2) 그것이 자연수 집합과 같은 카디널리티 (크기)를 가지면 (즉 번호-매길-수-있으면) 셀-수-있는 것입니다.[11] 동등하게, 집합이 만약 그것이 자연수 집합의 일부 부분집합(subset)과 같은 카디널리티를 가지면 셀-수-있는 것입니다. 그렇지 않으면, 그것은 셀-수-없는 것입니다.

Formal overview without details

정의에 의해, 집합 S는 만약 S에서 자연수(natural numbers) N = {0, 1, 2, 3, ...}로의 단사 함수(injective function) f : S → N가 존재하면 셀-수-있는 것입니다.

집합을 다른 클래스로 나누는 것이 자연스러워 보일 수 있습니다: 하나의 원소를 포함하는 모든 집합을 함께 모으십시오; 두 원소를 포함하는 모든 집합을 함께 모으십시오; ...; 마지막으로, 모든 무한 집합을 함께 모우고 그것들을 같은 크기를 가지는 것으로 생각해 보십시오. 이 견해는 크기의 자연적인 정의 아래에서, 어쨌든, 유지할 수 없습니다.

이것을 정교하게 하기 위해, 우리는 전단사(bijection)의 개념을 요구합니다. 비록 "전단사"가 숫자보다 더 진보된 개념처럼 보일지라도, 집합 이론의 관점에서 수학의 보통의 발전은 숫자 전에 함수를 정의하는데, 왜냐하면 그것들이 훨씬 더 단순한 집합에 기반을 두기 때문입니다. 이것이 전단사의 개념이 들어오는 곳입니다: 다음 대응을 정의합니다,

a ↔ 1, b ↔ 2, c ↔ 3

{a, b, c}의 모든 각 원소가 {1, 2, 3}의 정확하게 하나의 원소와 쌍을 이루고, 그 반대의 경우도 마찬가지이므로, 이것은 전단사를 정의합니다.

우리는 이제 이 상황을 일반화하고 두 집합을 같은 크기의 것으로 정의하는 것과 그것들 사이에 전단사가 있는 것은 필요충분 조건입니다. 모든 유한 집합에 대해, 이것은 "같은 크기"의 보통의 정의를 제공합니다.

무한 집합에 대한 것일 때, 집합 A = {1, 2, 3, ... }, 양의 정수(integer)의 집합과 B = {2, 4, 6, ...}, 짝수 양의 정수의 집합을 생각해 보십시오. 우리는, 우리의 정의 아래에서, 이들 집합이 같은 크기를 가지고, B는 셀-수-있는 무한임을 주장합니다. 이것을 입증하기 위해, 우리는 그들 사이에 전단사를 보여줄 필요가 있음을 회상하십시오. 이것은 다음이 되도록 할당 n ↔ 2n을 사용하여 달성될 수 있습니다:

1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....

앞의 예에서와 같이, A의 모든 각 원소는 정확하게 B의 하나의 원소와 쌍을 이루고, 그 반대의 경우도 마찬가지입니다. 그러므로 그것들은 같은 크기를 가집니다. 이것은 유한 집합에 대해 불가능한 것인 적절한 부분집합 중 하나와 같은 크기의 집합의 예제입니다.

마찬가지로, 자연수의 모든 순서화된 쌍의 집합은 그림에 있는 것과 같은 경로를 따름으로써 보일 수 있듯이 셀-수-있는 무한입니다:

The Cantor pairing function assigns one natural number to each pair of natural numbers

결과 매핑은 다음처럼 진행됩니다:

0 ↔ (0,0), 1 ↔ (1,0), 2 ↔ (0,1), 3 ↔ (2,0), 4 ↔ (1,1), 5 ↔ (0,2), 6 ↔ (3,0) ....

이 매핑은 모든 그러한 순서화된 쌍을 덮습니다.

만약 각 쌍이 일반 분수(vulgar fraction)의 분자(numerator)와 분모(denominator)로 취급되면, 모든 각 양의 분수에 대해, 우리는 그것에 대응하는 고유한 숫자를 얻을 수 있습니다. 이 표현은 역시 자연수를 포함하는데, 왜냐하면 모든 각 자연수가 역시 분수 N/1이기 때문입니다. 따라서 우리는 양의 정수가 있는만큼 양의 유리수가 정확히 있음을 결론내릴 수 있습니다. 이것은 역시 아래에서 보일 수 있듯이 모든 유리수에 대해 참입니다.

정리: 유한하게 많은 셀-수-있는 집합의 데카르트 곱(Cartesian product)은 셀-수-있는 것입니다.

이 형식의 삼각형 매핑(mapping)은, 처음 두 원소를 자연수로의 반복적으로 매핑함으로써, 유한하게 많은 자연수의 벡터(vectors)로 재귀적(recursively)으로 일반화합니다. 예를 들어, (0,2,3)은 39에 매핑하는 (5,3)에 매핑합니다.

때때로 하나보다 많은 매핑이 유용합니다: 셀-수-있는 무한인 것으로 표시되는 집합이 또 다른 집합 위로 매핑되며, 그런-다음 이 다른 집합이 자연수에 위로 매핑됩니다. 예를 들어, 양의 유리수(rational number)는 자연수 쌍(의 부분집합)에 쉽게 매핑될 수 있는데, 왜냐하면 p/q는 (p, q)로 매핑하기 때문입니다.

다음 정리는 셀-수-있는 무한 집합의 무한 부분집합에 관여합니다.

정리: 셀-수-있는 집합의 모든 각 부분집합은 셀-수-있는 것입니다. 특히, 셀-수-있는 무한 집합의 모든 각 무한 부분집합은 셀-수-있는 무한입니다.[12]

예를 들어, 소수(prime number)의 집합은 n-번째 소수를 n에 매핑함으로써 셀-수-있는 것입니다:

  • 2는 1로 매핑합니다
  • 3은 2로 매핑합니다
  • 5는 3으로 매핑합니다
  • 7은 4로 매핑합니다
  • 11은 5로 매핑합니다
  • 13은 6으로 매핑합니다
  • 17은 7로 매핑합니다
  • 19는 8로 매핑합니다
  • 23은 9로 매핑합니다
  • ...

역시 N보다 "자연적으로 더 큰" 것인 집합이 있습니다. 예를 들어, Z, 모든 정수(integer)의 집합 또는 Q, 모든 유리수(rational number)의 집합은 직관적으로 N보다 훨씬 더 크게 보일 수 있습니다. 그러나 보이는 것은 속일 수 있으며, 우리는 다음에 대해 주장합니다:

정리: Z (모든 정수의 집합) 및 Q (모든 유리수의 집합)는 셀-수-있는 것입니다.

유사한 방식에서, 대수적 숫자(algebraic number)의 집합은 셀-수-있는 것입니다.[13]

이들 사실은 많은 사람들이 비-직관적이라고 생각하는 결과에서 쉽게 따릅니다.

정리: 셀-수-있는 집합의 임의의 유한 합집합(union)은 셀-수-있는 것입니다.

셀-수-없는 집합이 있다는 것을 알고 있는 선견지명과 함께, 우리가 이 마지막 결과가 더 이상 밀려날 수 있는지 궁금할 수 있습니다. 그 대답은 "예"와 "아니오"이며, 우리는 그것을 확장할 수 있지만, 우리는 그렇게 하기 위해 새로운 공리를 가정하는 것이 필요합니다.

정리: (셀-수-있는 선택의 공리(axiom of countable choice)를 가정하여) 셀-수-있게 많은 셀-수-있는 집합의 합집합은 셀-수-있는 것입니다.

예를 들어, 셀-수-있는 집합 a, b, c, ...이 주어지면,

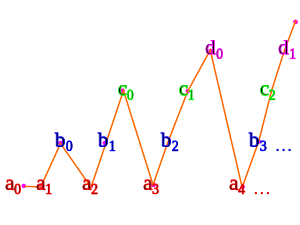
Enumeration for countable number of countable sets

우리가 위에서 본 삼각형 열거의 변형을 사용하여:

  • a0은 0에 매핑합니다
  • a1은 1에 매핑합니다
  • b0은 2에 매핑합니다
  • a2은 3에 매핑합니다
  • b1은 4에 매핑합니다
  • c0은 5에 매핑합니다
  • a3은 6에 매핑합니다
  • b2은 7에 매핑합니다
  • c1은 8에 매핑합니다
  • d0은 9에 매핑합니다
  • a4은 10에 매핑합니다
  • ...

이것은 만약 집합 a, b, c, ...가 서로소(disjoint)이면 오직 작동합니다. 만약 그렇지 않다면, 합집합은 훨씬 더 작고 따라서 역시 이전 정리에 의해 셀-수-있는 것입니다.

우리는 모든 집합 a, b, c, ...를 동시에 색인하기 위해 셀-수-있는 선택의 공리(axiom of countable choice)를 필요로 합니다.

정리: 자연수의 모든 유한-길이 수열(sequence)의 집합이 셀-수-있는 것입니다.

이 집합이 길이-1 수열, 길이-2 수열, 길이-3 수열의 합집합이며, 이것의 각각이 셀-수-있는 집합 (유한 데카르트 곱)입니다. 따라서 우리는 셀-수-있는 집합의 셀-수-있는 합집합에 대해 얘기하며, 이것이 이전 정리에 의해 셀-수-있는 것입니다.

정리: 자연수의 모든 유한 부분집합(subset)의 집합은 셀-수-있는 것입니다.

임의의 유한 부분집합의 원소는 유한 수열로 순서화될 수 있습니다. 오직 셀-수-있게 많은 유한 수열이 있으므로, 역시 오직 셀-수-있게 많은 유한 부분집합이 있습니다.

다음 정리는 전단사 함수 또는 전사 함수(surjective function)의 관점에서 동등한 공식화를 제공합니다. 이 결과의 증명은 랭의 텍스트에 발견될 수 있습니다.[3]

(기본) 정리: S를 집합으로 놓습니다. 다음 명제는 동등합니다:

  1. S가 셀-수-있는 것, 즉, 단사 함수 f : S → N가 존재합니다.
  2. S가 빈 것 또는 전사 함수 g : N → S가 존재합니다.
  3. S가 유한인 것 또는 전단사(bijection) h : N → S가 존재합니다.

따름정리: S와 T를 집합으로 놓습니다.

  1. 만약 함수 f : S → T가 단사이고 T가 셀-수-있는 것이면 S는 셀-수-있는 것입니다.
  2. 만약 함수 g : S → T가 전사이고 S가 셀-수-있는 것이면 T는 셀-수-있는 것입니다.

칸토의의 정리(Cantor's theorem)는 만약 A가 집합이고 P(A)가 그것의 거듭제곱 집합(power set), 즉, A의 모든 부분집합의 집합이면, A에서 P(A)로의 전사 함수가 없다고 주장합니다. 증명은 기사 칸토어의 정리(Cantor's theorem)에서 제공됩니다. 이것과 위의 기본 정리의 즉각적인 결과로, 우리는 다음을 가집니다:

제안: 집합 P(N)이 셀-수-있는 것이 아닙니다; 즉, 그것은 셀-수-없는(uncountable) 것입니다.

이 결과의 고심한 내용에 대해 칸토어의 대각선 논증(Cantor's diagonal argument)을 참조하십시오.

실수(real number)의 집합은 셀-수-없는 것이고 (칸토어의 첫 번째 셀-수-없음-속성 증명(Cantor's first uncountability proof)을 참조하십시오), 자연수의 모든 무한 수열(sequence)의 집합도 마찬가지입니다.

Some technical details

위의 섹션에서 명제의 증명은 특정 속성을 가진 함수의 존재에 의존합니다. 이 섹션은 이 역할에 공통적으로 사용되는 함수를 제공하지만, 이들 함수가 필수 요구된 속성을 가지는지 검증하는 내용은 없습니다. 기본 정리와 그것의 따름정리는 종종 증명을 단순화하기 위해 사용됩니다. 해당 정리에서 N은 임의의 셀-수-있는 무한 집합으로 대체될 수 있음을 관찰하십시오.

제안: 임의의 유한 집합(finite set)은 셀-수-있는 것입니다.

증명: S를 그러한 집합으로 놓습니다. 두 경우는 고려될 수 있습니다: S가 빈 것 또는 그것이 아닌 것으로 고려됩니다. 1.) 빈 집합은 심지어 자체도 자연수의 부분집합이므로, 그것은 셀-수-있는 것입니다. 2.) S가 비-빈이고 유한이면, 유한성의 정의에 의해 S와 일부 양의 자연수 n에 대해 집합 {1, 2, ..., n} 사이에 전단사이 있습니다. 이 함수는 S에서 N으로 단사입니다.

제안: 셀-수-있는 집합의 임의의 부분집합은 셀-수-있는 것입니다.[14]

증명: 그것의 도메인(domain)의 부분집합에 대한 단사 함수의 제한은 여전히 단사입니다.

제안: 만약 S가 셀-수-있는 집합이면 S ∪ {x}는 셀-수-있는 것입니다.[15]

증명: 만약 x ∈ S이면, 보일 수 있는 어떤 것이 없습니다. 그렇지 않으면, f: S → N를 단사라고 놓습니다. g(x) = 0에 의한 g: S ∪ {x} → N와 S에서 모든 y에 대해 g(y) = f(y) + 1를 정의하십시오. 이 함수 g는 단사입니다.

제안: 만약 A와 B가 셀-수-있는 집합이면 A ∪ B는 셀-수-있는 것입니다.[16]

증명: f: A → N와 g: B → N를 단사로 놓습니다. 만약 x가 A 안에 있으면 h(x) = 2f(x)에 의한 새로운 단사 h: A ∪ B → N와 만약 x가 B 안에 있지만 A 안에 있지 않으면 새로운 단사 h(x) = 2g(x) + 1를 정의합니다.

제안: 두 셀-수-있는 집합 A와 B의 데카르트 곱(Cartesian product)은 셀-수-있는 것입니다.[17]

증명: N × N가 정의의 결론으로 셀-수-있는 것인데 왜냐하면 f(m, n) = 2m3n에 의해 주어진 함수 f : N × N → N가 단사임을 관찰하십시오.[18] 그런-다음 기본 정리와 따름정리에서 임의의 두 셀-수-있는 집합의 데카르트 곱이 셀-수-있는 것임을 따릅니다. 이것은 만약 A와 B가 셀-수-있는 것이면 전사 f : N → A와 g : N → B가 있기 때문입을 따릅니다. 따라서 다음은

f × g : N × N → A × B

셀-수-있는 집합 N × N에서 집합 A × B로의 전사이고 따름정리는 A × B가 셀-수-있는 것임을 의미합니다. 이 결과는 셀-수-있는 집합의 임의의 유한 모음의 데카르트 곱으로 일반화되고 그 증명은 모음에서 집합의 숫자에 대한 귀납법(induction)에 의해 따릅니다.

제안: 정수(integers) Z는 셀-수-있는 것이고 유리수(rational numbers) Q는 셀-수-있는 것입니다.

증명: 정수 Z가 셀-수-있는 것인데 왜냐하면 만약 n이 비-음수이면 f(n) = 2n과 만약 n이 음수이면 f(n) = 3− n에 의해 주어진 함수 f : Z → N는 단사 함수이기 때문입니다. 유리수 Q가 셀-수-있는 것인데 왜냐하면 g(m, n) = m/(n + 1)에 의해 주어진 함수 g : Z × N → Q는 셀-수-있는 집합 Z × N에서 유리수 Q로의 전사이기 때문입니다.

제안: 대수적 숫자(algebraic number) A는 셀-수-있는 것입니다.

증명: 정의에 대해, (복소수를 포함하여) 모든 각 대수적 숫자는 정수 계수를 갖는 다항식의 근입니다. 대수적 숫자 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \alpha} 가 주어지면, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle a_0x^0+a_1x^1+a_2x^2+ \cdots + a_nx^n} 를 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \alpha} 가 다항식의 k번째 근임을 만족하는 정수 계수를 갖는 다항식으로 놓으며, 여기서 근은 작은 것에서 큰 것까지 절댓값에 의해 정렬되고, 그런-다음 작은 것에서 큰 것까지 인수에 의해 정렬됩니다. 우리는 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle f(\alpha) = 2^{k-1} \cdot 3^{a_0} \cdot 5^{a_1} \cdot 7^{a_2} \cdots {p_{n+2}}^{a_n}} 에 의해 주어진 단사 (즉, 일-대-일) 함수 f : A → Q를 정의할 수 있으며, 여기서 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle p_n} 은 n-번째 소수(prime)입니다.

제안: 만약 An가 N에서 각 n에 대해 셀-수-있는 집합이면 모든 An의 합집합은 역시 셀-수-있는 것입니다.[19]

증명: 이것은 각 n에 대해 전사 함수 gn : N → An가 있고 따라서 G(n, m) = gn(m)에 의해 주어진 다음 함수가 전사라는 사실의 결론입니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle G : \mathbf{N} \times \mathbf{N} \to \bigcup_{n \in \mathbf{N}} A_n} .

N × N가 셀-수-있는 것이므로, 따름정리는 합집합이 셀-수-있는 것임을 의미합니다. 우리는 N에서 An로의 전사의 비-빈 모음으로부터 N 전사 gn에서 각 n에 대해 선택하기 위해 이 증명에서 셀-수-있는 선택의 공리(axiom of countable choice)를 사용합니다.

실수의 셀-수-없음-성질에 대해 토폴로지적 증명은 유한 교집합 속성(finite intersection property)에서 설명됩니다.

Minimal model of set theory is countable

만약 ZFC 집합 이론의 표준 모델인 집합이 있으면 (안의 모델(inner model)을 참조하십시오), 최소 표준 모델이 있습니다 (구성-가능 우주(Constructible universe)을 참조하십시오). Löwenheim–Skolem 정리를 사용하여이 최소 모델이 셀 수 있음을 보여줄 수 있습니다. "불덧셈가능성"이라는 개념은이 모델에서도 의미가 있으며 특히이 모델 M에는 다음과 같은 요소가 포함되어 있습니다. 뢰벤하임–스콜렘 정리(Löwenheim–Skolem theorem)는 이 최소 모델이 셀-수-있는 것임을 보이기 위해 사용될 수 있습니다. "셀-수-없음-속성"이라는 개념은 심지어 이 모델에서 의미가 있고, 특히 이 모델 M이 다음과 같은 원소를 포함한다는 사실은:

  • M의 부분집합, 따라서 셀-수-있는 것,
  • 그러나 M의 관점에서 셀-수-있는 것,

집합 이론의 초기에는 역설적으로 보였으며, 자세한 것에 대해 스콜렘의 역설(Skolem's paradox)을 참조하십시오.

최소 표준 모델은 모든 대수적 숫자(algebraic number)와 모든 효과적으로 계산-가능 초월적 숫자(transcendental number), 마찬가지로 모든 다른 종류의 숫자를 포함합니다.

Total orders

셀-수-있는 집합은 다양한 방법에서 전체적으로 순서화된(totally ordered) 것일 수 있습니다. 예를 들어:

  • 바른-순서(Well-order) (역시 순서-숫자(ordinal number)를 참조하십시오):
    • 자연수 (0, 1, 2, 3, 4, 5, ...)의 보통 순서
    • 순서 (0, 1, 2, 3, ...; −1, −2, −3, ...)에서 정수
  • 다른 것 (바른 순서가 아님):
    • 정수 (..., −3, −2, −1, 0, 1, 2, 3, ...)의 보통 순서
    • 유리수의 보통 순서 (순서화된 목록으로 명시적으로 쓸 수 없습니다!)

여기서 바른 순서의 두 예제에서, 임의의 부분집합은 최소 원소를 가집니다; 그리고 비-바른 순서의 두 예제에서, 일부 부분집합은 최소 원소를 가지지 않습니다. 이것은 전체 순서가 역시 바른 순서인지 여부를 결정하는 핵심 정의입니다.

See also

Notes

  1. ^ Rudin 1976, Chapter 2
  2. ^ Kamke 1950, p. 2
  3. ^ a b Lang 1993, §2 of Chapter I
  4. ^ Apostol 1969, Chapter 13.19
  5. ^ Since there is an obvious bijection between N and N* = {1, 2, 3, ...}, it makes no difference whether one considers 0 a natural number or not. In any case, this article follows ISO 31-11 and the standard convention in mathematical logic, which takes 0 as a natural number.
  6. ^ "Comprehensive List of Set Theory Symbols". Math Vault. 2020-04-11. Retrieved 2020-09-06.
  7. ^ Halmos 1960, p. 91, calls S countable if a bijective mapping between a subset of S and N exists. Kamke 1950, p. 2, requires a bijective mapping between S and N.
  8. ^ Stillwell, John C. (2010), Roads to Infinity: The Mathematics of Truth and Proof, CRC Press, p. 10, ISBN 9781439865507, Cantor's discovery of uncountable sets in 1874 was one of the most unexpected events in the history of mathematics. Before 1874, infinity was not even considered a legitimate mathematical subject by most people, so the need to distinguish between countable and uncountable infinities could not have been imagined.
  9. ^ Cantor 1878, p. 242.
  10. ^ Ferreirós 2007, pp. 268, 272–273.
  11. ^ Weisstein, Eric W. "Countable Set". mathworld.wolfram.com. Retrieved 2020-09-06.
  12. ^ "9.2: Countable Sets". Mathematics LibreTexts. 2017-09-20. Retrieved 2020-09-06.
  13. ^ Kamke 1950, pp. 3–4
  14. ^ Halmos 1960, p. 91
  15. ^ Avelsgaard 1990, p. 179
  16. ^ Avelsgaard 1990, p. 180
  17. ^ Halmos 1960, p. 92
  18. ^ Avelsgaard 1990, p. 182
  19. ^ Fletcher & Patty 1988, p. 187

References

Look up countable in Wiktionary, the free dictionary.

Retrieved from "https://dawoum.duckdns.org/w/index.php?title=Countable_set&oldid=83839"