Cubic equation

Original article: w:Cubic equation

This article is about cubic equations in one variable. For cubic equations in two variables, see cubic plane curve.

Graph of a cubic function with 3 real roots (where the curve crosses the horizontal axis—where y = 0). The case shown has two critical points. Here the function is f(x) = (x³ + 3x² − 6x − 8)/4.

대수학(algebra)에서, 하나의 변수에서 삼차(입방) 방정식(cubic equation)는 다음 형식의 방정식(equation)입니다:

$ax^{3}+bx^{2}+cx+d=0$

여기서 a는 비-영입니다.

이 방정식의 해는 그 방정식의 왼쪽 변에 의해 정의되는 삼차 함수(cubic function)의 근(roots)이라고 불립니다. 만약 삼차 방정식의 계수(coefficients) a, b, c, 및 d의 모두는 실수(real number)이면, 그것은 적어도 하나의 실근을 가집니다 (이것은 모든 홀수-차수 다항 함수(polynomial function)에 대해 참입니다). 삼차 방정식의 근의 모두는 다음 방법으로 찾아질 수 있습니다:

• 대수적으로(algebraically), 즉, 그들은 네 계수, 네 기본 산술 연산(arithmetic operation) 및 n-번째 근(n-th roots, radicals)을 포함하는 삼차 공식(cubic formula)에 의해 표현될 수 있습니다. (이것은, 아벨–루피니 정리(Abel–Ruffini theorem)에 의한, 이차(quadratic) 및 사차(quartic) 방정식에서 역시 참이지만, 더 높은 방정식에서 참이 아닙니다.)
• 삼각법적으로(trigonometrically)
• 근의 수치적 근사(numerical approximation)는 뉴턴의 방법(Newton's method)과 같은 근-찾기 알고리듬(root-finding algorithm)을 사용하여 찾아질 수 있습니다.

계수는 실수가 될 필요는 없습니다. 아래에서 다룰 내용의 대부분은 2 및 3 이외의 특성(characteristic)을 가진 임의의 필드(field)에서 계수에 대해 유효합니다. 삼차 방정식의 해는 계수와 같은 필드에 반드시 속할 필요는 없습니다. 예를 들어, 유리수 계수를 가진 일부 삼차 방정식은 무리수 (및 심지어 비-실수) 복소수(complex number)인 근을 가집니다.

History

삼차 방정식은 고대 바빌로니아인, 그리스인, 중국인, 인디언, 및 이집트인에게 알려졌습니다. (기원전 20에서 16세기까지) 바빌로니아(Babylonia) 쐐기뼈 태블릿은 삼차와 삼차 근을 계산하기 위한 테이블과 함께 발견되어 왔습니다. 바빌로니아 사람들은 삼차 방정식을 풀기 위해 그 테이블을 사용했을 것이지만, 그들이 그렇게 했다는 것을 확인할 수 있는 흔적은 존재하지 않습니다. 정육면체 두배(doubling the cube)의 문제는 가장 단순하고 가장 오래된 연구된 삼차 방정식이고, 고대 이집트 사람들이 해가 존재하지 않을 것이라고 믿었던 것 중에 하나입니다. 기원전 5세기에서, 히포크라테스(Hippocrates)는 이 문제를 한 직선과 그의 길이가 두 배인 또 다른 두 직선 사이의 두 개의 평균 비례를 찾는 문제로 줄였지만, 컴퍼스와 직선자 구성(compass and straightedge construction)과 함께 이 문제를 해결할 수 없었을 것인데, 이 임무는 현재 불가능한 것으로 알려져 있습니다. 삼차 방정식을 푸는 방법은 기원전 약 2세기에 수집되고 3세기에 유 휘(Liu Hui)에 의해 주석이 달린 중국 수학(Chinese mathematical) 텍스트, The Nine Chapters on the Mathematical Art에 나타납니다. 기원후 3세기에서, 그리스 수학자(Greek mathematician) 디오판토스(Diophantus)는 일부 이변수 삼차 방정식 (디오판토스 방정식(Diophantine equations))에 대해 정수 또는 유리수 해를 찾았습니다. 히포크라테스(Hippocrates), 메나이크모스(Menaechmus) 및 아르키메데스(Archimedes)는, 비록 레비얼 네츠(Reviel Netz)와 같은 역사학자들은 그리스인이 삼차 방정식에 대해 생각하고 있었던 것 또는 단지 문자가 삼차 방정식으로 이어질 수 있었던 것인지에 대해 논쟁하고 있을지라도, 교차하는 원뿔 단면(conic sections)을 사용하여 정육면체 두배의 문제를 해결하기 위해 가까워지는 것으로 믿었습니다. 아르키메데스의 작품을 전부 번역한 토마스 히스(Thomas Heath)와 같은 일부 사람들은 동의하지 않고, 아르키메데스가 두 원뿔(conics)의 교차를 사용하여 삼차 방정식을 실제로 풀었고 근(root)이 0, 1 또는 2인 조건에 대해 역시 논의했다는 증거를 제시했습니다.

Graph of the cubic function f(x) = 2x³ − 3x² − 3x + 2 = (x + 1) (2x − 1) (x − 2)

7세기에서, 당나라(Tang dynasty) 천문학자이자 수학자 왕 효통(Wang Xiaotong)은 Jigu Suanjing이라는 그의 수학적 논문에서 형식 x³ + px² + qx = N의 25 삼차 방정식, p, q ≠ 0와 함께 그들의 23, q = 0와 함께 그들의 둘을 체계적으로 확립하고 수치적으로(numerically) 풀었습니다.

11세기에서, 페르시아 시인-수학자 오마르 카야얌(Omar Khayyám) (1048–1131)은 삼차 방정식의 이론에서 상당한 진전을 이루었습니다. 초기 논문에서, 그는 삼차 방정식이 하나 이상의 해를 가질 수 있는 것을 발견했고, 그것은 컴퍼스와 직선자 구성을 사용하여 절대 해결할 수 없다는 것을 말했습니다. 그는 기하학적 해(geometric solution)를 역시 찾았습니다. 그의 후기 작품, Treatise on Demonstration of Problems of Algebra에서, 그는 교차하는 원뿔 단면(conic section)에 의해 발견된 일반적인 기하학적 해와 함께 삼차 방정식의 완전한 분류를 작성했습니다.

12세기에서, 인도의 수학자 바스카라 2세는 일반적인 결과없이 삼차 방정식의 해를 시도했습니다. 어쨌든, 그는 삼차 방정식: x³ + 12x = 6x² + 35의 하나의 예제를 제공했습니다. 12세기에서, 또 다른 페르시아(Persian) 수학자, 샤라프 알-딘 알-천(Sharaf al-Dīn al-Tūsī) (1135–1213)은 Al-Muʿādalāt (방정식에 대한 논문)을 썼으며, 그것은 양의 해를 갖는 삼차 방정식의 여덟 가지 유형과 양의 해를 갖지 않을 수 있는 삼차 방정식의 다섯 가지 유형을 다루었습니다. 그는 삼차 방정식의 근(root)을 수치적으로(numerically) 근사화하기 위해 나중에 "루피니(Ruffini)-호너(Horner) 방법"으로 알려지게 되는 것을 사용했습니다. 그는 양의 해를 가지지 않을 수 있는 삼차 방정식을 풀기 위해 곡선의 최댓값과 최솟값(maxima and minima)의 개념을 역시 사용했습니다. 그는 삼차 방정식의 특정 유형에 대한 대수적 해를 찾기 위해 삼차 방정식의 판별식(discriminant)의 중요성을 이해했습니다.

그의 책 Flos에서, 피보나치(Fibonacci) (1170–1250)로 역시 알려진, 레오나르도 데 피사는 삼차 방정식 x³ + 2x² + 10x = 20에 대한 양의 해를 거의 근사할 수 있었습니다. 바빌로니아 숫자 시스템(Babylonian numerals)으로 쓰면 그는 1,22,7,42,33,4,40 (1 + 22/60 + 7/60² + 42/60³ + 33/60⁴ + 4/60⁵ + 40/60⁶와 동등한) 결과를 제공했으며, 이것은 약 10⁻⁹의 상대 오차(relative error)를 가집니다.

16세기 초에서, 이탈리아 수학자 시피오니 델 페로(Scipione del Ferro) (1465–1526)는 삼차 방정식의 클래스, 즉 형식 x³ + mx = n의 그들을 구하는 방법을 찾았습니다. 사실, 모든 입방 방정식은, 만약 우리가 m과 n을 음수인 것을 허용하면, 이 형태로 줄어들 수 있지만, 음수(negative number)는 그 때 당시에 그에게 알려지지 않았습니다. 델 페로는, 자신의 학생 안토니오 피오르(Antonio Fior)에게 그것에 대해 말했을 때, 그의 죽음 바로 직전까지 그의 업적을 비밀로 유지했습니다.

Niccolò Fontana Tartaglia

1530년, 니콜로 타르탈리아(Niccolò Tartaglia) (1500–1557)는 주안 다 코이(Zuanne da Coi)로부터 삼차 방정식에서 두 가지 문제를 받았고 그것을 해결할 수 있다고 발표했습니다. 그는 곧 피오르의 도전을 받았고, 두 사람 사이에 유명한 대회로 이어졌습니다. 각 참가자는 일정량의 돈을 넣어야 했고 그의 라이벌이 해결해야 하는 많은 문제를 냈습니다. 30일 이내에 더 많은 문제를 해결 한 사람은 모든 돈을 얻을 것입니다. 타르탈리아는 형식 x³ + mx = n으로 질문을 받았으며, 그것에 대해 그는 일반적인 방법을 연구했습니다. 피오르는 형식 x³ + mx² = n으로 질문을 받았는데, 그가 그것을 해결하기에 너무 어려웠고, 타르탈리아가 대회에서 이겼습니다.

나중에, 타르탈리아는 제롤라모 카르다노(Gerolamo Cardano) (1501–1576)에 의해 삼차 방정식을 해결하는 것에 대해 비밀을 밝히도록 설득되었습니다. 1539년, 타르탈리아는 카르다노가 그것을 절대 공개하지 않을 것 그리고 만약 그가 삼차에 대한 책을 쓰게 되면, 그는 출판하기 위해 타르탈리아에게 시간을 제공해야 할 것이라는 조건에서 오직 그렇게 했습니다. 몇 년 후, 카르다노는 델 페로의 이전 연구에 대해 배웠고 1545년 그의 책 Ars Magna에서 델 페로의 방법을 출판했는데, 이것은 카르다노가 (독립적 해에 대해 타르탈리아에게 주어진 신용과 함께) 그의 결과를 출판하기 위해 타르탈리아에게 6년을 제공했다는 의미입니다. 타르탈리아에 대한 카르다노의 약속은 그가 타르탈리아의 연구를 출판하지 않을 것이라고 말했던 것이었고, 카르다노는, 약속을 지키기 위해, 델 페로의 것을 출판하는 것이라고 느꼈습니다. 그럼에도 불구하고, 이것은 타르탈리아로부터 카르다노로의 도전으로 이어졌지만, 카르다노는 그것을 거절했습니다. 도전은 카로다노의 학생 로도비코 페라리(Lodovico Ferrari) (1522–1565)에 의해 결국 받아들여졌습니다. 페라리는 경쟁에서 타르탈리아보다 우수했고, 타르탈리아는 명성과 수입을 모두 잃었습니다.

카르다노는 타르탈리아의 방법이 때때로 음수의 제곱근을 추출하는 것을 요구한다는 것을 알게 되었습니다. 그는 심지어 Ars Magna에서 이들 복소수(complex number)를 가진 계산을 포함했지만, 그는 그것을 실제로 이해하지는 못했습니다. 라파엘 봄벨리(Rafael Bombelli)는 이 문제를 자세하게 연구했고 그러므로 복소수의 발견자로 종종 여겨집니다.

프랑수아 비에트(François Viète) (1540–1603)는 세 개의 실수 근을 가진 삼차에 대해 삼각법 해를 독립적으로 도출했고, 르네 데카르트(René Descartes) (1596–1650)는 비에타의 연구을 확장했습니다.

Factorization

만약 삼차 방정식의 계수가 유리수(rational number)이면, 우리는 모든 계수에 그들 분모의 공통 배수(common multiple)를 곱함으로써, 정수 계수를 가진 동등한 방정식을 얻을 수 있습니다. 정수 계수를 가진 그러한 방정식

$ax^{3}+bx^{2}+cx+d=0,$

은, 만약 왼쪽 변의 다항식이 더 낮은 차수의 다항식의 곱이면 비-기약(reducible:가약)이라고 말합니다. 가우스의 보조 정리(Gauss's lemma)에 의해, 만약 방정식이 비-기약이면, 우리는 인수가 정수 계수를 가진 것으로 생각할 수 있습니다.

비-기약 삼차 방정식의 근을 찾는 것이 일반적인 경우를 해결하는 것보다 더 쉽습니다. 사실, 만약 방정식이 비-기약이면, 인수 중 하나는 반드시 차수가 1을 가지고, 따라서 다음 형식을 가집니다:

$qx-p$

여기서 q와 p는 서로소 정수(coprime integers)입니다. 유리수 근 테스트(rational root test)는 유한한 숫자의 경우를 검사함으로써 q와 p를 찾는 것을 허용합니다 (왜냐하면 q는 반드시 a의 약수이고, p는 반드시 d의 약수이기 때문입니다).

따라서, 하나의 근은 $\textstyle x_{1}={\frac {p}{q}}$이고 다른 근들은 다른 인수의 근이며, 이것은 다항식 긴 나눗셈(polynomial long division)에 의해 구할 수 있습니다. 이 다른 인수는 다음입니다:

${\frac {a}{q}}x^{2}+{\frac {bq+ap}{q^{2}}}x+{\frac {cq^{2}+bpq+ap^{2}}{q^{3}}}$

(계수는 정수가 아닌 것처럼 보이지만, 만약 p / q가 근이면 반드시 정수여야 합니다.)

그런 다음, 다른 근들은 이 이차 다항식(quadratic polynomial)의 근이고 이차 공식(quadratic formula)을 사용함으로써 구할 수 있습니다.

Depressed cubic

다음 형식의 삼차는 눌린 것이라고 말합니다:

$t^{3}+pt+q$

그들은 일반적인 삼차보다 훨씬 더 단순하지만, 기본적인데, 왜냐하면 임의의 삼차의 연구는 간단한 변수의 변경(change of variable)으로 눌린 삼차의 그것으로 감소될 수 있기 때문입니다.

다음 방정식을 삼차 방정식으로 놓습니다:

$ax^{3}+bx^{2}+cx+d=0$

다음 변수의 변경은 t²에 항이 없는 삼차를 결과로써 생성합니다:

$x=t-{\frac {b}{3a}}$

양쪽 변을 a로 나눈 후에, 우리는 다음 눌린 삼차 방정식을 얻습니다:

$t^{3}+pt+q=0,$

여기서

${\begin{aligned}t=&x+{\frac {b}{3a}}\\p=&{\frac {3ac-b^{2}}{3a^{2}}}\\q=&{\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}.\end{aligned}}$

원래 방정식의 근(roots) $x_{1},x_{2},x_{3}$는, $i=1,2,3$에 대해, 관계

$x_{i}=t_{i}-{\frac {b}{3a}}$

에 의해 눌러진 방정식의 근 $t_{1},t_{2},t_{3}$와 관련됩니다.

Discriminant and nature of the roots

삼차의 근(roots)의 본성 (실수 또는 아닌 것, 구별되는 것 또는 아닌 것)은, 판별식(discriminant)을 사용함으로써, 명시적으로 그들을 계산하지 않고 결정될 수 있습니다.

Discriminant

다항식(polynomial)의 판별식(discriminant)은 그의 계수의 함수입니다. 그것이 영인 것과 다항식이 중복 근(multiple root)을 가지는 것, 또는 그것이 비-상수 다항식의 제곱으로 나뉘는 것은 필요충분 조건입니다. 달리 말해서, 판별식이 비-영인 것과 다항식이 제곱-없는(square-free) 것은 필요충분 조건입니다.

만약 r₁, r₂, r₃이 삼차 $ax^{3}+bx^{2}+cx+d$의 세 근(roots)이면 (구별되는 것 또는 실수(real)인 것을 요구하지 않습니다), 판별식은 다음입니다:

$a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}.$

눌린 삼차 $t^{3}+pt+q$의 판별식은 다음입니다:

$-\left(4\,p^{3}+27\,q^{2}\right).$

일반적인 삼차 $ax^{3}+bx^{2}+cx+d$의 판별식은 다음입니다:

$18\,abcd-4\,b^{3}d+b^{2}c^{2}-4\,ac^{3}-27\,a^{2}d^{2}.$

그것은 $a^{4}$과 눌린 삼차에 해당하는 판별식의 곱입니다. 이들 두 판별식 중 하나가 영인 것과 다른 하나가 역시 영인 것은 필요충분 조건이고, 만약 계수가 실수(real)이면, 두 판별식은 같은 부호를 가지는 것이 따릅니다. 요약하면, 같은 정보는 이들 두 판별식으로부터 추론될 수 있습니다.

앞의 공식을 증명하기 위해, 우리는 모든 것을 r₁, r₂, r₃, 및 a에서 다항식으로 표현하기 위해 비에타의 공식(Vieta's formulas)을 사용할 수 있습니다. 증명은 그런 다음 두 다항식의 상등의 검증에서 결과로 생깁니다.

Nature of the roots

만약 다항식의 계수가 실수(real number)이고 판별식 $\Delta$가 영이 아니면, 두 경우가 있습니다:

• 만약 $\Delta >0$이면, 삼차는 세 구별되는 실수 근(roots)을 가집니다.
• 만약 $\Delta <0$이면, 삼차는 하나의 실수 근과 두 비-실수 복소수 켤레(complex conjugate) 근을 가집니다.

이것은 다음으로 입증될 수 있습니다. 먼저, 만약 r이 실수 계수를 갖는 다항식의 근이면, 그의 복소수 켤레(complex conjugate)는 역시 하나의 근입니다. 그래서 비-실수 근은, 만약 있다면, 복소수 켤레 근의 쌍으로 발생합니다. 삼차 다항식은 대수학의 기본 정리(fundamental theorem of algebra)에 의해 (필수적으로 구별되는 것은 아닌) 세 근을 가지므로, 적어도 하나의 근은 반드시 실수여야 합니다.

위에서 말한 것처럼, 만약 r₁, r₂, r₃이 삼차 $ax^{3}+bx^{2}+cx+d$의 세 근이면, 판별식은 다음입니다:

$\Delta =a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}$

만약 세 근이 실수이고 구별되면, 판별식은 양의 실수의 곱, 즉, $\Delta >0$입니다.

만약 오직 하나의 근, 말하자면 r₁이 실수이면, r₂와 r₃는 복소수 켤레이며, 이것은 r₂ – r₃는 순수한 허수(purely imaginary number:순허수)이고, 따라서 (r₂ – r₃)²는 실수이고 음수임을 의미합니다. 다른 한편으로, r₁ – r₂와 r₁ – r₃가 복소수 켤레이고, 그들의 곱이 실수이고 양수입니다. 따라서 판별식은 하나의 음의 실수와 여러 양의 실수의 곱입니다. 즉 $\Delta <0$입니다.

Multiple root

만약 삼차의 판별식이 영이면, 삼차는 중복 근(multiple root)을 가지고, 그의 모든 근은 실수입니다.

눌러진 삼차 $t^{3}+pt+q$의 판별식은, 만약 $4p^{3}+27q^{2}=0$이면, 영과 같습니다. 만약 p가 역시 영이면, p = q = 0이고, 0은 삼차의 삼중 근입니다. 만약 $4p^{3}+27q^{2}=0$이고 p ≠ 0이면, 삼차는 다음의 하나의 단순 근

$t_{1}={\frac {3q}{p}}$

과 다음의 하나의 이중 근을 가집니다:

$t_{2}=t_{3}={\frac {-3q}{2p}}.$

달리 말해서,

$t^{3}+pt+q=\left(t-{\frac {3q}{p}}\right)\left(t+{\frac {3q}{2p}}\right)^{2}.$

이 결과는 후자의 곱을 전개함으로써 입증될 수 있거나 비에타의 공식에서 나오는 꽤 간단한 방정식의 시스템(system of equations)을 해결함으로써 검색될 수 있습니다.

눌러진 삼차의 감소(reduction of a depressed cubic)를 사용함으로써, 이들 결과는 일반적인 삼차에 대해 확장될 수 있습니다. 이것은 제공합니다:만약 삼차 $ax^{3}+bx^{2}+cx+d$의 판별식이 영이면, 다음 중 하나입니다. 만약 $b^{2}=3ac$이면, 삼차는 하나의 삼중 근을 가집니다:

$x_{1}=x_{2}=x_{3}={\frac {-b}{3a}},$

및

$ax^{3}+bx^{2}+cx+d=a\left(x+{\frac {b}{3a}}\right)^{3}$

또는, 만약 $b^{2}\neq 3ac$이면, 삼차는 하나의 이중 근

$x_{2}=x_{3}={\frac {9ad-bc}{2(b^{2}-3ac)}},$

및 하나의 다음의 단순 근을 가집니다:

$x_{1}={\frac {4abc-9a^{2}d-b^{3}}{a(b^{2}-3ac)}}.$

따라서

$ax^{3}+bx^{2}+cx+d=a\left(x-x_{1}\right)\left(x-x_{2}\right)^{2}.$

Characteristic 2 and 3

위의 결과는, 계수가 2 또는 3 이외의 특성(characteristic)의 필드(field)에 속하면 유효하지만, 2와 3에 의한 관련된 나눗셈 때문에, 특성 2 또는 3에 대해 수정되어야 합니다.

눌러진 삼차의 감소은 특성 2에 대해 작동하지만, 특성 3에 대해 그렇지 않습니다. 두 경우 모두에서, 그것은 수립하기 더 간단하고 일반적인 삼차에 대해 결과를 말합니다. 그것에 대해 주요 도구는 중복 근이 다항식과 그의 형식적 도함수(formal derivative)의 공통 근이라는 사실입니다. 이들 특성에서, 만약 도함수가 상수가 아니면, 그것은 특성 3에서 선형인 하나의 근, 또는 특성 2에서 선형 다항식의 제곱을 가집니다. 이것은 중복 근을 계산하는 것을 허용하고, 세 번째 근은 그의 합으로부터 추론될 수 있으며, 그것은 비에타의 공식(Vieta's formulas)에 의해 제공됩니다.

다른 특성과의 차이는, 특성 2에서 이중 근에 대해 공식은 제곱 근(square root)을 포함하고, 특성 3에서, 삼중 근에 대해 공식은 세제곱 근(cube root)을 포함한다는 것입니다.

Cardano's formula

제롤라모 카르다노(Gerolamo Cardano)는 삼차 방정식을 푸는 것에 대해 첫 번째 공식을 공인 받았습니다. 그의 공식은 눌린 삼차에 적용되지만, § Depressed cubic에서 보인 것처럼, 그것은 모든 삼차 방정식을 푸는 것을 허용합니다.

카르다노의 원래 결과는 다음의 것인데, 만약

$x^{3}+px+q=0$

이 p와 q가 $4p^{3}+27q^{2}>0$를 만족하는 실수(real number)를 갖는 삼차 방정식이면, 방정식은 다음 실수 근을 가집니다:

${\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.$

이 결과를 얻는 것에 대한 여러 방법에 대해, 아래의 § Derivation of the roots를 참조하십시오.

§ Nature of the roots에 보인 것처럼, 이 경우에서, 두 다른 근은 비-실수 복소수 켤레(complex conjugate) 숫자입니다. 그것은 나중에 보여졌는데 (카르다노는 복소수(complex number)를 알지 못했습니다) 두 다른 근은 단위의 주요 세제곱 근(primitive cube root of unity) ${\frac {-1+i{\sqrt {3}}}{2}}$에 의한 세제곱 근의 하나, 및 ${\frac {-1-i{\sqrt {3}}}{2}}$에 의한 다른 하나의 세제곱 근을 곱합으로써 얻습니다.

만약 $4p^{3}+27q^{2}<0$이면, 세 실수 근이 있지만, 갈루아 이론(Galois theory)은 그들이 오직 실수를 포함하는 대수적 표현(algebraic expression)에 의해 절대 표현될 수 없음을 입증하는 것을 허용합니다. 그러므로, 방정식은 카르다노의 시대의 지식과 함께 이 경우에서 절대 풀려지지 않습니다. 이 경우는, 따라서, 라틴어에서 기약 경우를 의미하는, casus irreducibilis으로 불려져 왔습니다.

casus irreducibilis에서, 카르다노의 공식은 여전히 사용될 수 있지만, 일부 주의가 세제곱 근을 사용에서 필요됩니다. 첫 번째 방법은 근 함수의 주요 값(principal value)을 나타내는 것으로 기호 ${\sqrt {{~}^{~}}}$ 및 ${\sqrt[{3}]{{~}^{~}}}$를 정의하는 것입니다 (그것이 가장 큰 실수 부분을 가진 근입니다). 이 관례와 함께, 세 근에 대해 카르다노의 공식은 유효하게 남지만, 순수하게 대수적은 아닌데, 왜냐하면 주요 부분의 정의는 순수하게 대수적은 아닌데, 그것은 실수 부분을 비교하는 것에 대해 부등식을 포함하기 때문입니다. 또한, 주요 세제곱 근의 사용은, 만약 계수가 비-실수 복소수이면, 잘못된 결과를 제공할 수 있습니다. 게다가, 만약 계수가 또 다른 필드(field)에 속하면, 주요 세제곱 근은 일반적으로 정의되지 않습니다.

카르다노의 공식을 항상 올바르게 만드는 것에 대해 두 번째 방법은 두 세제곱 근의 곱이 반드시 –p / 3여야 함을 주의하는 것입니다. 그것은 방정식의 근이 다음인 것의 결과로써 생깁니다:

$C-{\frac {p}{3C}}\quad {\text{with}}\quad C={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.$

이 공식에서, 기호 ${\sqrt {{~}^{~}}}$ 및 ${\sqrt[{3}]{{~}^{~}}}$는 임의의 제곱 근과 임의의 세제곱 근을 나타냅니다. 방정식의 다른 근은 세제곱 근의 변경하는 것 또는, 동등하게 단위의 주요 세제곱 근, 즉 $\textstyle {\frac {-1\pm {\sqrt {-3}}}{2}}$에 의한 세제곱 근을 곱함으로써 얻어질 수 있습니다.

근에 대해 이 공식은 p = q = 0일 때, 만약 q = 0이면, C ≠ 0을 가지는 것에 대해 제곱 근을 선택하는 조건 아래의 경우를 제외하고 항상 정확합니다. 비슷하게, 공식은, $4p^{3}+27q^{2}=0$일 때 및 삼차 다항식이 기약(irreducible)이 아닐 때인, 세제곱 근이 요구되지 않는 다른 경우에서 역시 쓸모없습니다.

이 공식은, p와 q가 2 또는 3 이외의 특성(characteristic)의 임의의 필드(field)에 속할 때, 역시 정확합니다.

General cubic formula

일반적인 삼차 방정식 (a ≠ 0을 가진)

$ax^{3}+bx^{2}+cx+d=0$

의 근에 대해 삼차 공식(cubic formula)은 눌린 삼차(depressed cubic)에 대한 축소에 의해 카르다노의 공식의 모든 각 변형으로부터 추론될 수 있습니다. 여기서 눌린 것인 변형은 실수 계수 뿐만 아니라, 2와 3과 다른 특성(characteristic)의 임의의 필드(field)에 속하는 계수 a, b, c, d에 역시 유효합니다.

공식은 꽤 복잡하므로 그것을 더 작은 공식으로 쪼갤 가치가 있습니다.

다음을 놓습니다:

${\begin{aligned}\Delta _{0}&=b^{2}-3ac,\\\Delta _{1}&=2b^{3}-9abc+27a^{2}d,\end{aligned}}$

및

$C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}},$

여기서 기호 ${\sqrt {{~}^{~}}}$ 및 ${\sqrt[{3}]{{~}^{~}}}$는, 각각, 임의의 제곱 근 및 임의의 세제곱 근을 나타냅니다. 제곱 근 앞의 기호 "±"는 "+" 또는 "–" 주에 하나입니다; 선택은 거의 임의적이고, 그것을 바꾸는 것은 결과적으로 제곱근의 변화에 이릅니다. 어쨌든, 만약 하나의 선택이 C = 0으로 이어지면, 다른 부호가 반드시 선택되어야 합니다. 그런-다음, 근의 하나는 다음입니다:

$x=-{\frac {1}{3a}}\left(b+C+{\frac {\Delta _{0}}{C}}\right){\text{.}}$

다른 두 근은 C의 정의에서 세제곱 근의 선택을 바꾸는 것 또는, 동등하게 단위의 주요 세제곱 근(primitive cube root of unity), 즉 –1 ± √–3/2을 C에 곱함으로써 얻어질 수 있습니다. 다른 말로, 세 근은 다음입니다:

$x_{k}=-{\frac {1}{3a}}\left(b+\xi ^{k}C+{\frac {\Delta _{0}}{\xi ^{k}C}}\right),\qquad k\in \{0,1,2\}{\text{,}}$

여기서 ξ = –1 + √–3/2입니다.

눌린 삼차의 특별한 경우에 관해서, 이 공식은 적용되지만 근이 세제곱 근없이 표현될 수 있을 때 쓸모가 없습니다.

Trigonometric and hyperbolic solutions

Trigonometric solution for three real roots

실수 계수를 가진 삼차 방정식은 세 실수 근을 가질 때, 제곱근의 관점에서 이들 근을 표현하는 공식은 복소수를 포함합니다. 갈루아 이론(Galois theory)은 세 근이 실수이고, 어느 것도 유리수가 아닐 때 (casus irreducibilis), 우리는 실수 제곱근의 관점에서 근을 절대 표현할 수 없음을 입증하는 것을 허용합니다. 그럼에도 불구하고, 해의 순수하게 실수 표현은, 특히 코사인(cosine) 및 아크코사인(arccosine)의 관점에서, 삼각 함수(trigonometric functions)를 사용하여 얻어질 수 있습니다. 보다 정확하게, 눌린 삼차(depressed cubic) $t^{3}+pt+q$의 근은 다음입니다:

$t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-{\frac {2\pi k}{3}}\right)\quad {\text{for}}\quad k=0,1,2.$

이 공식은 프랑수아 비에타(François Viète)에 기인합니다. 그것은 방정식이 세 실수 근을 가질 때 (즉, $4p^{3}+27q^{2}<0$) 순수하게 실수입니다. 그렇지 않으면, 그것은 여전히 정확하지만 오직 하나의 실수 근이 있을 때 복소수 코사인과 아크코사인을 포함하고, 그것은 p = 0)일 때 무의미합니다 (영에 의한 나눗셈).

이 공식은, § Depressed cubic에서 설명된 역 치환을 사용하여, 일반적인 삼차 방정식의 근에 대해 공식으로 직접적으로 변환될 수 있습니다. 그것은 다음으로 입증될 수 있습니다.

방정식 t³ + pt + q = 0으로 시작하여, t = u cos θ를 설정합니다. 아이디어는 방정식을 다음 항등식과 일치하도록 만드는 u를 선택하는 것입니다:

$4\cos ^{3}\theta -3\cos \theta -\cos(3\theta )=0\,.$

이것에 대해, $u=2{\sqrt {-{\frac {p}{3}}}}$를 선택하고 방정식을 ${\frac {u^{3}}{4}}$으로 나눕니다. 이것은 다음을 제공합니다:

$4\cos ^{3}\theta -3\cos \theta -{\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}=0\,.$

위의 항등식과 결합함으로써, 우리는 다음을 얻습니다:

$\cos(3\theta )={\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}},$

그리고 근은 따라서 다음입니다:

$t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-{\frac {2\pi k}{3}}\right)\quad {\text{for}}\quad k=0,1,2\,.$

Hyperbolic solution for one real root

오직 하나의 실수 근 (및 p ≠ 0)이 있을 때, 이 근은, 쌍곡선 함수(hyperbolic function)를 사용하여, 다음으로 비슷하게 표현될 수 있습니다:

${\begin{aligned}t_{0}&=-2{\frac {|q|}{q}}{\sqrt {-{\frac {p}{3}}}}\cosh \left({\frac {1}{3}}\operatorname {arcosh} \left({\frac {-3|q|}{2p}}{\sqrt {\frac {-3}{p}}}\right)\right)\quad {\text{if }}\quad 4p^{3}+27q^{2}>0{\text{ and }}p<0\,,\\t_{0}&=-2{\sqrt {\frac {p}{3}}}\sinh \left({\frac {1}{3}}\operatorname {arsinh} \left({\frac {3q}{2p}}{\sqrt {\frac {3}{p}}}\right)\right)\quad {\text{if }}\quad p>0\,.\end{aligned}}$

만약 p ≠ 0이고 오른쪽 변에 대한 부등식이 만족시켜지지 않으면 (세 실수 근의 경우에서), 공식은 유효하게 남지만 복소수 양을 포함합니다.

p = ±3일 때, t₀의 위의 값은 때때로 체비쇼프 세제곱 근(Chebyshev cube root)으로 불립니다. 보다 정확하게, 코사인 및 쌍곡선 코사인을 포함하는 값은 정의하고, p = −3일 때, 같은 해석적 함수(analytic function)는 C_1/3(q)를 나타내며, 이것은 적절한 체비쇼프 세제곱 근입니다. 쌍곡선 사인을 포함하는 값은, p = 3일 때, S_1/3(q)을 유사하게 표시됩니다.

Geometric solutions

Omar Khayyám's solution

Omar Khayyám's geometric solution of a cubic equation, for the case m = 2, n = 16, giving the root 2. The intersection of the vertical line on the x-axis at the center of the circle is happenstance of the example illustrated.

n > 0과 함께, 삼차 방정식 x³ + m²x = n을 푸는 것에 대해, 오마르 캬야암(Omar Khayyám)은 양의 x-축 위의 선분(line segment) [0, n/m²]을 지름으로 가지는 원, 포물선 y = x²/m을 구성하고, 원과 포물선이 x-축 위에서 교차하는 점을 통과하는 수직 직선을 구성했습니다. 해는 원점에서 수직 직선과 x-축의 교점까지 수평 선분의 길이에 의해 제공됩니다 (그림을 참조하십시오).

간단한 현대 증명은 다음입니다. 방정식에 x를 곱하고 항을 다시-묶으면 다음을 제공합니다:

${\frac {x^{4}}{m^{2}}}=x\left({\frac {n}{m^{2}}}-x\right).$

왼쪽 변은 포물선 위의 y²의 값입니다. 원의 방정식이 y² + x(x − n/m²) = 0이므로, 오른쪽 변은 원 위의 y²의 값입니다.

Solution with angle trisector

실수 계수를 가진 삼차 방정식은 컴퍼스-와-직선자(compass and straightedge), 및 각도 삼등분기(angle trisector)를 사용하여 기하학적으로 풀 수 있는 것과 그것이 세 실수 근을 가지는 것은 필요충분 조건입니다.

삼차 방정식은 (삼등분기없이) 컴퍼스-와-직선자로 풀 수 있는 것과 그것이 유리수(rational) 근을 가지는 것은 필요충분 조건입니다. 이것은, 고대 그리스의 수학자들(ancient Greek mathematicians)에 의해 세워진, 각도 삼등분(angle trisection)과 정육면체를 두 배(doubling the cube)의 오래된 문제는 컴퍼스-와-직선자 구성으로 절대 해결할 수 없다는 것을 의미합니다.

Geometric interpretation of the roots

Three real roots

For the cubic (1) with three real roots, the roots are the projection on the x-axis of the vertices A, B, and C of an equilateral triangle. The center of the triangle has the same abscissa as the inflection point.

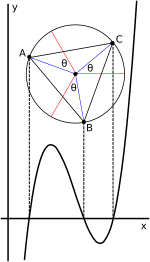
세-실수-근의 경우에서 근의 비에타의 삼각법 표현은 원의 관점에서 기하학적 해석에 그 자체를 빌려줍니다. 삼차가, 위에서 처럼, 눌린 형식 (2), t³ + pt + q = 0으로 쓰일 때, 해는 다음으로 표현될 수 있습니다:

$t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-k{\frac {2\pi }{3}}\right)\quad {\text{for}}\quad k=0,1,2\,.$

여기서 $\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)$는 단위 원에서 각도입니다; 그 각도의 1/3를 취하는 것은 복소수의 세제곱 근을 취하는 것에 해당합니다; k = 1, 2에 대해 −k2π/3를 더하여 다른 세제곱 근을 찾십니다; 그리고 이들 결과 각의 코사인에 $2{\sqrt {-{\frac {p}{3}}}}$를 곱하여 크기에 대해 정정합니다.

(첨부된 그래프에서 표시된) 비-눌린 경우 (1)에 대해, 이전에 표시된 것처럼 눌린 경우는 x = t − b/3a 그래서 t = x + b/3a를 만족하는 t를 정의함으로써 얻어질 수 있브니다. 그래픽적으로, 이것은, 각도 관계 변경없이, 변수 t와 x 사이를 변경할 때 수평적으로 단순히 그래프를 이동하는 것에 해당합니다. 이 이동은 변곡 점과 원의 중심을 y-축 위로 이동합니다. 결과적으로, t에서 방정식의 근은 합해져서 영이 됩니다.

One real complex root

In the Cartesian plane

The slope of line RA is twice that of RH. Denoting the complex roots of the cubic as g ± hi, g = OM (negative here) and h = √tan ORH = √slope of line RH = BE = DA.

삼차 함수(cubic function)의 그래프가 데카르트 평면(Cartesian plane)에서 그려질 때, 만약 실수 하나의 근이 있을 때, 그것은 곡선의 수평 절편 (그림의 점 R)의 앱시서(abscissa) (x-좌표)입니다. 게다가, 만약 복소수 켤레 근이 g ± hi로 쓰이면, 실수 부분(real part) g는 삼차의 x-절편 R을 통과하는 삼차에 대한 접선(tangent line)의 접점 H의 앱시서입니다 (즉 부호화된 길이 RM, 그림에서 음수입니다). 허수 부분(imaginary part) ±h는 이 접선과 수평 축 사이의 각도의 탄젠트의 제곱 근입니다.

In the complex plane

하나의 실수와 두 복소수 근과 함께, 세 근은 복소 평면에서 점으로 표현될 수 있으며, 마찬가지로 삼차의 도함수의 두 근도 가능합니다. 모든 이들 근 사이의 흥미로운 기하학적 관계가 있습니다.

세 근을 나타내는 복소 평면에서 점은 이등변 삼각형의 꼭짓점으로 제공됩니다. (삼각형은 이등변인데 왜냐하면 하나의 근은 수평 (실수) 축 위에 있고 복소수 켤레인, 다른 두 개의 근은 실수 축 위와 아래에 대칭으로 나타나기 때문입니다.) 마든의 정리(Marden's theorem)는 삼차의 도함수의 근을 나타내는 점은 삼각형의 슈타이너 내접-타원(Steiner inellipse)–그의 변의 중점에서 삼각형에 접하는 고유한 타원의 초점(foci)임을 말합니다. 만약 실수 축 위의 꼭짓점에서 각도가 π/3보다 작으면, 타원의 주요 축은 실수 축 위에 놓이며, 마찬가지로 그의 초점이 그렇고 따라서 도함수의 근이 그렇습니다. 만약 해당 각도가 π/3보다 크면, 주요 축은 수직 직선이고 그의 초점, 도함수의 근은 복소수 켤레입니다. 그리고 만약 해당 각도가 π/3이면, 삼각형은 정삼각형이며, 슈타이너 내접-타원은 단순히 삼각형의 내접원이며, 그의 초점은 내접원의-중심에서 서로 일치하며, 이것은 실수 축 위에 놓이고, 그러므로 도함수는 중복 실수 근을 가집니다.

Galois group

2와 3과 다른 특성(characteristic) k의 필드에 걸쳐 삼차 기약 다항식(irreducible polynomial)이 주어지면, k에 걸쳐 갈루아 그룹(Galois group)은 (분할 필드(splitting field)) k의 가장-작은 확장의 k를 고정하는 필드 자기-동형(field automorphism) 그룹입니다. 이들 자기-동형은 다항식의 근을 순열해야 하므로, 이 그룹은 세 근의 모든 여섯 순열의 그룹 S₃, 또는 세 원형 순열의 그룹 A₃ 중의 하나입니다.

삼차의 판별식 Δ는 다음의 제곱입니다:

${\sqrt {\Delta }}=a^{2}(r_{1}-r_{2})(r_{1}-r_{3})(r_{2}-r_{3}),$

여기서 a는 삼차의 선행 계수이고, r₁, r₂ 및 r₃는 삼차의 세 근입니다. ${\sqrt {\Delta }}$는, 만약 두 근이 교환되면, 부호의 변화이므로, ${\sqrt {\Delta }}$가, 만약 갈루아 그룹이 A₃이면 오직 갈루아 그룹에 의해 고정됩니다. 달리 말해서, 갈루아 그룹이 A₃인 것과 판별식이 k의 원소의 제곱인 것은 필요충분 조건입니다.

대부분 정수는 제곱이 아니므로, 유리수(rational number)의 필드 Q에 걸쳐 작업할 때, 대부분 기약 삼차 다항식의 갈루아 그룹은 여섯 원소를 가진 그룹 S₃입니다. 세 원소를 가진 갈루아 그룹 A₃의 예제는 p(x) = x³ − 3x − 1로 제공되며, 그의 판별식은 81 = 9²입니다.

Derivation of the roots

이 섹션은 카르다노의 공식(Cardano's formula)을 유도하는 것에 대해 여러 방법을 재편성합니다.

Cardano's method

이 방법은 시피오니 델 페로(Scipione del Ferro)와 타르탈리아(Tartaglia)에 기인하지만, 제롤라모 카르다노(Gerolamo Cardano)의 이름을 따서 명명되었으며, 그는 그의 책 Ars Magna (1545)에서 그것을 처음으로 출판했습니다.

이 방법은 눌린 삼차 t³ + pt + q = 0에 적용됩니다. 그 아이디어는 u + v = t를 만족하는 두 변수 u와 v를 도입하고 이것을 눌린 삼차로 치환하는 것이며, 다음을 제공합니다:

$u^{3}+v^{3}+(3uv+p)(u+v)+q=0.$

이 시점에서 카르다노는 조건 3uv + p = 0을 강제했습니다. 이것은 이전 등식에서 세 번째 항을 제거하여, 다음 방정식 시스템으로 이어집니다:

${\begin{aligned}u^{3}+v^{3}&=-q\\uv&=-{\frac {p}{3}}.\end{aligned}}$

u³ 및 v³의 합과 곱을 알면, 우리는 그들이 다음 이차 방정식(quadratic equation)의 두 해라는 것을 추론합니다:

$(x-u^{3})(x-v^{3})=x^{2}-(u^{3}+v^{3})x+u^{3}v^{3}=x^{2}-(u^{3}+v^{3})x+(uv)^{3}=0,$

그래서

$x^{2}+qx-{\frac {p^{3}}{27}}=0,$

이 방정식의 판별식은 $\Delta =q^{2}+{\frac {4p^{3}}{27}}$이고, 그것이 양수임을 가정하면, 이 방정식에 대한 실수 해는 다음입니다 (제곱 근 아래에서 4로 나눗셈 후에)

$-{\frac {q}{2}}\pm {\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}.$

그래서 (u 또는 v 선택에서 일반성의 손실 없이):

$u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.$

$v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.$

u + v = t이므로, 이들 해의 세제곱 근의 합은 만약 그 방정식이면 근입니다. 즉

$t={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}$

은 그 방정식의 근입니다; 이것이 카르다노의 공식입니다.

이것은 $4p^{3}+27q^{2}>0$일 때 잘 작동하지만, 만약 $4p^{3}+27q^{2}<0$이면, 공식에서 나타나는 제곱 근은 실수가 아닙니다. 복소수(complex number)가 세제곱 근을 가지므로, 주의없이 카르다노의 공식을 사용하면 아홉 근을 제공할 것인데, 반면에 삼차 방정식은 절대 세 근보다 많이 가지지 못합니다. 이것은 라파엘 봄벨리(Rafael Bombelli)에 의해 그의 책 L'Algebra (1572)에서 처음으로 명확해졌습니다. 그 해는 uv = –p/3, 즉 v = –p/3u이라는 사실을 사용한 것입니다. 이것은, 오직 하나의 세제곱 근이 계산되어야 하고, § Cardano's formula에서 주어진 두 번째 공식으로 이어짐을 의미합니다.

그 방정식의 다른 근은 세제곱 근을 바꾸는 것, 또는, 동등하게, 세제곱 근에 두 개의 단위의 주요 세제곱 근(primitive cube roots of unity), 즉 ${\frac {-1\pm {\sqrt {-3}}}{2}}$의 각각을 곱함으로써 획득될 수 있습니다.

Vieta's substitution

비에타의 치환은 1615년 사후에 출판된 텍스트에서 프랑수아 비에트(François Viète) (비에타는 그의 라틴어 이름입니다)에 의해 도입된 방법이며, § Cardano's method의 두 번째 공식을 직접 제공하고, 두 개의 다른 세제곱 근을 계산하는 문제를 피합니다.

눌린 삼차 t³ + pt + q = 0에서 시작하여, 비에타의 치환은 t = w – p/3w입니다.

치환 t = w – p/3w은 눌린 삼차를 다음으로 변환합니다.

$w^{3}+q-{\frac {p^{3}}{27w^{3}}}=0.$

w³를 곱하여, 우리는 w³에서 다음 이차 방정식을 얻습니다:

$(w^{3})^{2}+q(w^{3})-{\frac {p^{3}}{27}}=0.$

다음

$W=-{\frac {q}{2}}\pm {\sqrt {{\frac {p^{3}}{27}}+{\frac {q^{2}}{4}}}}$

을 이차 방정식의 임의의 비-음의 근으로 놓습니다. 만약 w₁, w₂ 및 w₃은 W의 세 개의 세제곱 근(cube root)이면, 원래 눌린 삼차의 근은 w₁ − p/3w₁, w₂ − p/3w₂, 및 w₃ − p/3w₃입니다. 이차 방정식의 다른 근은 $\textstyle -{\frac {p^{3}}{27W}}$입니다. 이것은 제곱 근의 부호를 변경하여 i = 1, 2, 3에 대해 w_i 및 − p/3w_i을 서로 바꾸고, 따라서 근을 바꾸지 않는 것을 의미합니다. 이 방법은, 이차 방정식의 두 근 모두가 영일 때, 즉 p = q = 0일 때, 오직 실패하며, 그 경우에서 눌린 삼차의 유일한 근은 0입니다.

Lagrange's method

그의 논문 Réflexions sur la résolution algébrique des équations ("방정식의 대수적 푸는 것에 대한 생각")에서, 조제프 루이 라그랑주(Joseph Louis Lagrange)는 균등 방법에서 낮은 차수의 방정식을 해결하기 위한 새로운 방법 도입했으며, 그는 그것을 더 높은 차수에 대해 일반화될기를 희망했습니다. 이 방법은 삼차 및 사차 방정식(quartic equation)에 대해 잘 작동하지만, 라그랑주는 그것을 오차 방정식(quintic equation)에 적용하는 것에서 성공하지 못했는데, 왜냐하면 그것은 최소 육차의 분해 다항식을 푸는 것을 요구하기 때문입니다. 그 문제를 해결하기 전에 아무도 성공하지 못했다는 것을 제외하고, 이것은 차수 5 이상의 대수적 공식의 비-존재의 첫 번째 징후였습니다. 이것은 나중에 증명되었고, 아벨–루피니 정리(Abel–Ruffini theorem)라고 이름 지어졌습니다. 그럼에도 불구하고, 해결-가능한 오차 방정식을 푸는 현대적인 방법은 주로 라그랑주의 방법을 기초로 합니다.

삼차 방정식의 경우에서, 라그랑주의 방법은 카르다노의 것과 같은 해를 제공합니다. 라그랑주의 방법은 일반적인 삼차 방정식 ax³ + bx² + cx + d = 0에 직접 적용될 수 있지만, 계산은 눌린 삼차 방정식, t³ + pt + q = 0과 함께 더 간단합니다.

라그랑주의 주요 아이디어는 근 자체 대신에 근의 이산 푸리에 변환(discrete Fourier transform)으로 작동하는 것이었습니다. 보다 정확하게, ξ를 단위의 원시 세 번째 근(primitive third root of unity), 즉 ξ³ = 1 및 ξ² + ξ + 1 = 0을 만족하는 숫자로 놓습니다 (복소수의 공간에서 작동할 때, 우리는 $\textstyle \xi ={\frac {-1\pm i{\sqrt {3}}}{2}}=e^{2i\pi /3}$를 가지지만, 이 복소수 해석은 여기서 사용되지 않습니다). x₀, x₁ 및 x₂를 풀어야 할 삼차 방정식의 세 근으로 나타내면, 다음

${\begin{aligned}s_{0}&=x_{0}+x_{1}+x_{2},\\s_{1}&=x_{0}+\xi x_{1}+\xi ^{2}x_{2},\\s_{2}&=x_{0}+\xi ^{2}x_{1}+\xi x_{2},\end{aligned}}$

을 근의 이산 푸리에 변환으로 놓습니다. 만약 s₀, s₁ 및 s₂가 알려지면, 근은 이 선형 변환을 역함으로써 구성되는 역 푸리에 변환과 함께 그들로부터 다시-구할 수 있습니다; 즉,

${\begin{aligned}x_{0}&={\tfrac {1}{3}}(s_{0}+s_{1}+s_{2}),\\x_{1}&={\tfrac {1}{3}}(s_{0}+\xi ^{2}s_{1}+\xi s_{2}),\\x_{2}&={\tfrac {1}{3}}(s_{0}+\xi s_{1}+\xi ^{2}s_{2}).\end{aligned}}$

비에타의 공식(Vieta's formulas)에 의해, s₀가 눌린 삼차의 경우에서 영, 일반적인 삼차에 대해 −b/a가 되는 것으로 알려져 있습니다. 그래서, 오직 s₁ 및 s₂가 계산될 필요가 있습니다. 그들은 근의 대칭 함수(symmetric functions) (x₁ 및 x₂가 서로 바꾸면 s₁ 및 s₂가 역시 서로 바뀝니다)가 아니지만, s₁ 및 s₂의 일부 간단한 대칭 함수는 풀어야 할 삼차 방정식의 근에서 역시 대칭입니다. 따라서 이들 대칭 함수는 원래 삼차의 (알려진) 계수의 관점에서 표현될 수 있고, 이것은 알려진 계수와 함께 다항식의 근으로 s_i를 표현하는 것을 결국 허용합니다.

삼차 방정식의 경우에서, P=s₁s₂, 및 S=s₁³ + s₂³은 그러한 대칭 다항식입니다 (아래를 참조하십시오). 그것은 s₁³ 및 s₂³가 이차 방정식 z² − Sz + P³ = 0의 두 근인 것을 따릅니다. 따라서 방정식의 분해는 카르다노의 방법, u 및 v의 자리에서 s₁ 및 s₂와 함께 정확하게 완료될 수 있습니다.

눌린 삼차의 경우에서, 우리는 x₀ = 1/3(s₁ + s₂) 및 s₁s₂ = −3p을 가지며, 반면에 카르다노의 방법에서 우리는 x₀ = u + v 및 uv = −1/3p을 설정했습니다. 따라서, 우리는, u 및 v을 교환까지(up to), s₁ = 3u 및 s₂ = 3v를 가집니다. 달리 말해서, 이 경우에서, 카르다노의 방법과 라그랑주의 방법은, 임의의 변수에서 세 개의 인수까지(up to), 정확히 같은 것을 계산하며, 주요 차이는 라그랑주의 방법은 이들 임의의 변수가 그 문제에서 나타나는 이유를 설명하는 것입니다.

Computation of S and P

관계 ξ³ = 1 및 ξ² + ξ + 1 = 0을 사용하여 간단한 계산은 다음을 제공합니다:

${\begin{aligned}P&=s_{1}s_{2}=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}-(x_{0}x_{1}+x_{1}x_{2}+x_{2}x_{0}),\\S&=s_{1}^{3}+s_{2}^{3}=2(x_{0}^{3}+x_{1}^{3}+x_{2}^{3})-3(x_{0}^{2}x_{1}+x_{1}^{2}x_{2}+x_{2}^{2}x_{0}+x_{0}x_{1}^{2}+x_{1}x_{2}^{2}+x_{2}x_{0}^{2})+12x_{0}x_{1}x_{2}.\end{aligned}}$

이것은 P와 Q가 근의 대칭 함수임을 보여줍니다. 뉴턴의 항등식(Newton's identities)을 사용하여, 근의 기본 대칭 함수(elementary symmetric functions)의 관점에서 그들을 표현하는 것은 간단합니다. 눌린 삼차의 경우에서 e₁ = 0, e₂ = p와 e₃ = −q와 함께, 및 일반적인 경우에서 e₁ = −b/a, e₂ = c/a와 e₃ = −d/a와 함께 다음을 제공합니다:

${\begin{aligned}P&=e_{1}^{2}-3e_{2},\\S&=2e_{1}^{3}-9e_{1}e_{2}+27e_{3},\end{aligned}}$.

Applications

삼차 방정식은 다양한 다른 문맥에서 발생합니다.

In mathematics

• 각도 삼등분(Angle trisection) 및 정육면체를 두 배(doubling the cube)는 직선자와 컴퍼스 구성(straightedge and compass construction)에 의해 해결될 수 없는 것으로 입증된 기하학(geometry)의 두 고대의 문제인데, 왜냐하면 그들은 삼차 방정식을 푸는 것과 동등하기 때문입니다.
• 마든의 정리(Marden's theorem)는 임의의 삼각형의 슈타이너 내접-타원(Steiner inellipse)의 초점(foci)은 그의 근이 삼각형의 세 꼭짓점의 복소 평면(complex plane)에서 좌표인 삼차 함수를 사용함으로써 찾아질 수 있다고 말합니다. 이 삼차의 첫 번째 도함수의 근은 그들 초점의 복소수 좌표입니다.
• 정규 칠각형(heptagon)의 넓이(area)는 삼차의 근의 관점에서 표현될 수 있습니다. 게다가, 긴 대각선과 변, 변과 짧은 대각선, 및 짧은 대각선의 음수와 긴 대각선의 비율은 모두 특정 삼차 방정식을 만족시킵니다. 또한, 칠각 삼각형(heptagonal triangle)의 내접-반지름(inradius)과 외접-반지름(circumradius)의 비율은 삼차 방정식의 해 중 하나입니다. $2\pi /7$와 관련된 각도의 삼각 함수의 값은 삼차 방정식을 만족시킵니다.
• 임의의 각도의 코사인 (또는 다른 삼각 함수)가 주어지면, 그 각도의 3분의 1(one-third of that angle)의 코사인은 삼차의 근 중에 하나입니다.
• 일반적인 사차 방정식(quartic equation)의 해는 그의 분해 삼차(resolvent cubic)의 해에 의존합니다.
• 3×3 행렬(matrix)의 고윳값(eigenvalue)은 행렬의 특성 다항식(characteristic polynomial)인 삼차 다항식의 근입니다.
• 삼-차 상수 계수 선형 미분 방정식(linear differential equation) 또는 차이 방정식(difference equation)의 특성 방정식(characteristic equation)은 삼차 방정식입니다.
• 삼차 베지에 곡선(Bézier curve)과 직선의 교점은 베지에 곡선을 나타내는 직접 삼차 방정식을 사용하여 계산될 수 있습니다.

In other sciences

• 해석적 화학(analytical chemistry)에서, 버퍼 용액(buffer solution)의 pH를 찾기 위해 사용될 수 있는 샬롯 방정식(Charlot equation)은 삼차 방정식을 사용하여 해결될 수 있습니다.
• 화학적 공학(chemical engineering) 및 열역학(thermodynamics)에서, (물질의 압력, 부피 및 온도와 관련된) 상태의 방정식(equations of state)은 부피에서 삼차입니다.
• 가속도의 비율(rates of acceleration)을 변화하는 것을 포함하여 운동 방정식(Kinematic equations)은 삼차입니다.
• 지진 레일리 파동의 속도는 레일리 파동(Rayleigh wave) 삼차 방정식의 해입니다.

References

• Guilbeau, Lucye (1930), "The History of the Solution of the Cubic Equation", Mathematics News Letter, 5 (4): 8–12, doi:10.2307/3027812, JSTOR 3027812

Further reading

• Anglin, W. S.; Lambek, Joachim (1995), "Mathematics in the Renaissance", The Heritage of Thales, Springers, pp. 125–131, ISBN 978-0-387-94544-6 Ch. 24.
• Dence, T. (November 1997), "Cubics, chaos and Newton's method", Mathematical Gazette, 81 (492), Mathematical Association: 403–408, doi:10.2307/3619617, ISSN 0025-5572, JSTOR 3619617
• Dunnett, R. (November 1994), "Newton–Raphson and the cubic", Mathematical Gazette, 78 (483), Mathematical Association: 347–348, doi:10.2307/3620218, ISSN 0025-5572, JSTOR 3620218
• Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
• Mitchell, D. W. (November 2007), "Solving cubics by solving triangles", Mathematical Gazette, 91, Mathematical Association: 514–516, doi:10.1017/S0025557200182178, ISSN 0025-5572
• Mitchell, D. W. (November 2009), "Powers of φ as roots of cubics", Mathematical Gazette, 93, Mathematical Association, ISSN 0025-5572
• Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007), "Section 5.6 Quadratic and Cubic Equations", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• Rechtschaffen, Edgar (July 2008), "Real roots of cubics: Explicit formula for quasi-solutions", Mathematical Gazette, 92, Mathematical Association: 268–276, doi:10.1017/S0025557200183147, ISSN 0025-5572
• Zucker, I. J. (July 2008), "The cubic equation – a new look at the irreducible case", Mathematical Gazette, 92, Mathematical Association: 264–268, doi:10.1017/S0025557200183135, ISSN 0025-5572

External links

• "Cardano formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• History of quadratic, cubic and quartic equations on MacTutor archive.
• 500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle? – YouTube video by Mathologer about the history of cubic equations and Cardano's solution, as well as Ferrari's solution to quartic equations