Field (mathematics)

수학(mathematics)에서, 필드(field)는 덧셈(addition), 뺄셈(subtraction), 곱셈(multiplication) 및 나눗셈(division)이 정의되고 유리수(rational)와 실수(real number) 위에 해당하는 연산이 행하는 것처럼 작동하는 집합(set)입니다. 필드는 따라서 대수학(algebra), 숫자 이론(number theory), 및 수학의 많은 다른 분야에서 널리 사용되는 기초적인 대수 구조(algebraic structure)입니다.

가장 잘 알려진 필드는 유리수(rational number) 필드, 실수(real number) 필드 및 복소수(complex number) 필드입니다. 유리 함수의 필드(fields of rational functions), 대수적 함수 필드(algebraic function field), 대수적 숫자 필드(algebraic number field), 및 p-진수 필드(p-adic fields)와 같은 많은 다른 필드가 수학, 특히 숫자 이론과 대수 기하학(algebraic geometry)에서 공통적으로 사용되고 연구됩니다. 대부분의 암호화 프로토콜(cryptographic protocol)은 유한 필드(finite field), 즉, 매우 많은 원소(elements)를 가진 필드에 의존합니다.

두 필드의 관계는 필드 확장(field extension)의 개념으로 표현됩니다. 1830년대 에바리스트 갈루아(Évariste Galois)에 의해 시작된 갈루아 이론(Galois theory)은 필드 확장의 대칭을 이해하는 것에 전념됩니다. 다른 결과 사이에, 이 이론은 각도 삼등분(angle trisection) 및 원을 정사격형화(squaring the circle)는 컴퍼스와 직선자(compass and straightedge)와 함께 절대 행해질 수 없음을 보여줍니다. 게다가, 그것은 오차 방정식(quintic equation)이 대수적으로 풀 수 없음을 보여줍니다.

필드는 여러 수학 도메인에서 기본 개념으로 사용됩니다. 이것은 덧셈의 구조를 가진 필드 위에 기초한 수학적 해석학(mathematical analysis)의 다른 가지를 포함합니다. 해석학에서 기본 정리는 실수 필드의 구조적 속성에 따라 정해집니다. 대수적 목적에 대해 가장 중요하게, 임의의 필드는 선형 대수(linear algebra)에 대해 표준 일반 문맥인, 벡터 공간(vector space)에 대해 스칼라(scalars)로 사용될 수 있을 것입니다. 유리수의 필드의 형제, 숫자 필드(Number field)는 숫자 이론(number theory)에서 깊게 연구됩니다. 함수 필드(Function fields)는 기하학적 대상의 속성을 설명하는 데 도움이 될 수 있습니다.

Definition

비공식적으로, 하나의 필드는 해당 집합 위에 정의된 두 연산(operation): $a + b$ 로 쓰인 덧셈 연산, 및 $a \cdot b$ 로 쓰인 곱셈 연산과 함께 하나의 집합이며, 그것의 둘 다는 유리수(rational)와 실수(real)에 대해 동작하는 것과 유사하게 동작하며, 모든 원소 a에 대한 덧셈의 역원(additive inverse) $-a$ 및 모든 각 비-영 원소 b에 대한 곱셈의 역원(multiplicative inverse) b⁻¹의 존재를 포함합니다. 이것은 우리에게, 다음을 정의함으로써, 뺄셈(subtraction) $a - b$ 과 나눗셈(division) $a / b$ 의 이른바 역 연산을 역시 고려하는 것을 허용합니다:

a - b = a + (- b)

,

a / b = a \cdot b -1

.

Classic definition

공식적으로, 필드는, 덧셈 및 곱셈으로 불리는 $F$ 위의 두 연산과 함께, 집합 $F$ 입니다.^[1] $F$ 위의 연산은 함수 $F \times F \to F$ — 다른 말로, $F$ 의 원소를 그의 원소의 모든 각 쌍에 결합하는 매핑입니다. $a$ 와 $b$ 의 덧셈의 결과는 $a$ 와 $b$ 의 합으로 불리고, $a + b$ 로 표시됩니다. 비슷하게, $a$ 와 $b$ 의 곱셈의 결과는 $a$ 와 $b$ 의 곱으로 불리고, $ab$ 또는 $a \cdot b$ 로 표시됩니다. 이들 연산은 필드 공리(field axioms)를 참조하는, 다음 속성을 만족시키는 것이 요구됩니다. 이들 공리에서, $a, b$ 및 $c$ 는 필드 $F$ 의 임의의 원소입니다.

덧셈과 곱셈의 결합-가능성(Associativity): $a + (b + c) = (a + b) + c$ 및 $a \cdot (b \cdot c) = (a \cdot b) \cdot c$ 입니다.
덧셈과 곱셈의 교환-가능성(Commutativity): $a + b = b + a$ 및 $a \cdot b = b \cdot a$ 입니다.
덧셈(Additive identity) 및 곱셈의 항등원(multiplicative identity): $a + 0 = a$ 및 $a \cdot 1 = a$ 를 만족하는 $F$ 안의 두 다른 원소 $0$ 과 $1$ 이 존재합니다.
덧셈의 역원(Additive inverse): $a + (- a) = 0$ 를 만족하는, a의 덧셈의 역원으로 불리고, $- a$ 으로 표시되는, $F$ 안의 원소가 존재합니다.
곱셈의 역원(Multiplicative inverse): $a \cdot a -1 = 1$ 를 만족하는, a의 곱셈의 역원으로 불리고, $a -1$ , $1/ a$ , 또는 $1 / a$ 으로 표시되는, $F$ 안의 원소가 존재합니다.
덧셈에 대한 곱셈의 분배-가능성(Distributivity): $a \cdot (b + c) = (a \cdot b) + (a \cdot c)$ 입니다.

이것은 다음으로 요약될 수 있습니다: 필드는 덧셈과 곱셈으로 불리는 두 연산을 가집니다; 그것은, 덧셈의 항등원(additive identity)으로 0을 갖는, 덧셈 아래의 아벨 그룹(abelian group)입니다; 비-영 원소는 곱셍의 항등원으로 1을 갖는 곱셈 아래에서 아벨 그룹을 형성합니다; 및 곱셈은 덧셈에 걸쳐 분배됩니다.

Alternative definitions

필드는 다른 방식으로 역시 정의될 수 있지만, 동등한 방법입니다. 우리는 네 이항 연산(덧셈, 뺄셈, 곱셈, 및 나눗셈) 및 그들의 요구된 속성에 의해 필드를 대안적으로 정의할 수 있습니다. 영에 의한 나눗셈(Division by zero)은, 정의에 따라, 제외됩니다.^[2] 존재적 한정어(existential quantifier)를 피하기 위해, 필드는 두 이항 연산(덧셈 및 곱셈), (각각, 덧셈 및 곱셈에 대한 역원 산출하는) 두 단항 연산, 및 두 영항(nullary) 연산 (상수 $0$ 및 $1$ )에 의해 정의될 수 있습니다. 이들 연산은 그런-다음 위의 조건을 준수합니다. 존재 한정어(existential quantifier)를 피하는 것은 구성적 수학(constructive mathematics) 및 컴퓨팅(computing)에서 중요합니다.^[3] 우리는 같은 두 이항 연산, 하나의 단항 연산 (곱셈의 역원), 및 $0 = 1 + (-1)$ 와 $- a = (-1) a$ 이므로, 두 상수 $1$ 과 $-1$ 에 의해 필드를 동등하게 정의할 수 있을 것입니다.^{[nb 1]}

Examples

Rational numbers

유리수는 필드의 개념을 고심하여 완성하기 전에 오랜 시간 동안 널리 사용되어 왔습니다. 그들은 $a$ 와 $b$ 가 정수이고, $b \neq 0$ 인 분수(fractions) $a / b$ 로 쓸 수 있는 숫자입니다. 그러한 분수의 덧셈의 역은 $- a / b$ 이고, ( $a \neq 0$ 인 것에 제공되는) 곱셈의 역은 $b / a$ 이고, 이것은 다음으로 알 수 있습니다:

{\frac {b}{a}}\cdot {\frac {a}{b}}={\frac {ba}{ab}}=1.

추상적으로 요구된 필드 공리는 유리수의 표준 속성으로 감소합니다. 예를 들어, 분배-가능성의 법칙은 다음으로 입증될 수 있습니다:^[4]

{\begin{aligned}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}+{\frac {e}{f}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}\cdot {\frac {f}{f}}+{\frac {e}{f}}\cdot {\frac {d}{d}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {cf}{df}}+{\frac {ed}{fd}}\right)={\frac {a}{b}}\cdot {\frac {cf+ed}{df}}\\[6pt]={}&{\frac {a(cf+ed)}{bdf}}={\frac {acf}{bdf}}+{\frac {aed}{bdf}}={\frac {ac}{bd}}+{\frac {ae}{bf}}\\[6pt]={}&{\frac {a}{b}}\cdot {\frac {c}{d}}+{\frac {a}{b}}\cdot {\frac {e}{f}}.\end{aligned}}

Real and complex numbers

덧셈과 곱셈의 보통 연산을 가진, 실수 $R$ 은 필드를 역시 형성합니다. 복소수(complex number) $C$ 는 다음 표현으로 구성됩니다:

a, b

실수를 가진,

a + bi,

여기서 $i$ 는 허수 단위(imaginary unit), 즉, $i 2 = -1$ 를 만족하는 (비-실수) 숫자입니다. 실수의 덧셈과 곱셈은, 이 유형의 표현이 모든 필드 공리를 만족시키고 따라서 $C$ 에 대해 유지되는 그러한 방법에서 정의됩니다. 예를 들어, 분배 법칙은 다음으로 강제로 수행합니다:

(a + bi)(c + di) = ac + bci + adi + bdi 2 = ac - bd + (bc + ad) i .

즉시 이것은 다시 위의 타입의 표현이 되고, 그래서 복소수는 필드를 형성합니다. 복소수는, 그들의 묘사하는 표현의 실수에 의해 제공된 데카르트 좌표과 함께, 또는 길이와 어떤 뚜렷한 방향에서 측정된 각에 의해 지정되는, 원점에서 이들 점까지 화살표로, 평면(plane)에서 점으로 기하학적으로 표현될 수 있습니다. 덧셈은, 그런-다음, (데카르트 좌표를 더하는) 직관적인 평행사변형에 화살표를 결합하는 것에 해당하고, 곱셈은 (각도는 더하고 길이는 곱하는) 화살표의 회전 및 스케일링을 –덜 직관적으로– 결합하는 것입니다. 실수와 복소수의 필드는 수학, 물리학, 공학, 통계학, 및 많은 다른 과학 분야를 관통하여 사용됩니다.

Constructible numbers

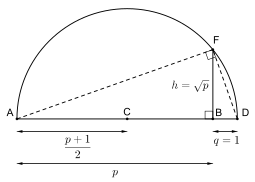
고대에서, 여러 기하학적 문제는 컴퍼스와 직선자(compass and straightedge)와 함께 어떤 숫자를 구성하는 실행-(불)가능성에 관계되었습니다. 예를 들어, 이런 방법으로 주어진 각을 삼등분하는 것이 일반적으로 불가능하다는 것이 그리스인에게 알려져 있지 않았습니다. 이들 문제는 구성-가능한 숫자(constructible numbers)의 필드를 사용하여 해결될 수 있습니다.^[5] 실수 구성-가능한 숫자는, 정의에 의해, 오직 컴퍼스(compass)와 직선자(straightedge)를 사용하여 유한하게 많은 단계에서 점 0과 1로부터 구성될 수 있는 선분의 길이입니다. 구성-가능한 숫자로 제한된, 실수의 필드 연산이 부여된, 이들 숫자는 필드를 형상허며, 이것은 유리수의 필드 $Q$ 를 적절하게 포함합니다. 그림은, $Q$ 안에 포함되는 것을 요구하지 않는, 구성-가능한 숫자의 제곱근(square root)의 구성을 보여줍니다. 그림에서 레이블링을 사용하여, 선분 $AB$ , $BD$ , 및 (중점(midpoint) $C$ 에 중심이 있는) $AD$ 에 걸친 반원(semicircle)을 작도하며, 이것은 점 $F$ 에서 B를 통과하는 수직(perpendicular) 직선과 교차하고, $BD$ 가 길이 1을 가질 때 $B$ 로부터 정확하게 $h={\sqrt {p}}$ 거리에 있습니다.

모든 실수가 구성-가능한 것은 아닙니다. ${\sqrt[{3}]{2}}$ 는 구성-가능한 숫자가 아님을 보일 수 있으며, 그것은 부피 2를 가진 정육면체의 변의 길이를 컴퍼스와 나침반으로 구성하는 것이 불가능한 것을 의미하고, 고대 그리스인에 의해 제기된 또 다른 문제입니다.

A field with four elements

Addition

Multiplication

+	$O$	$I$	$A$	$B$
$O$	$O$	$I$	$A$	$B$
$I$	$I$	$O$	$B$	$A$
$A$	$A$	$B$	$O$	$I$
$B$	$B$	$A$	$I$	$O$

·	$O$	$I$	$A$	$B$
$O$	$O$	$O$	$O$	$O$
$I$	$O$	$I$	$A$	$B$
$A$	$O$	$A$	$B$	$I$
$B$	$O$	$B$	$I$	$A$

유리수와 같은 익숙한 숫자 시스템 외에도, 필드의 다른 덜 즉각적인 예제가 있습니다. 다음 예제는 $O$ , $I$ , $A$ , 및 $B$ 로 불리는 네 원소로 구성되는 필드입니다. 표기법은 $O$ 가 (위의 공리에서 0으로 표시되는) 덧셈의 항등원의 역할을 하고, I는 (위의 공리에서 1로 표시되는) 곱셈의 항등원의 역할을 만족하는 것으로 선택됩니다. 필드 공리는 일부 더 많은 필드 이론을 사용, 또는 직접 계산에 의해 검증될 수 있습니다. 예를 들어,

A \cdot (B + A) = A \cdot I = A

, 이것은

A \cdot B + A \cdot A = I + B = A

과 같은데, 왜냐하면 분배-가능성에 의해 요구됩니다.

이 필드는 네 원소를 가진 유한 필드(finite field)로 불리고, $F 4$ 또는 $GF(4)$ 로 표시됩니다.^[6] (오른쪽에서 테이블 안의 빨간색으로 강조 표시된) $O$ 와 $I$ 로 구성된 부분-집합은, 이진 필드(binary field) $F 2$ 또는 $GF(2)$ 로 알려진, 역시 하나의 필드입니다. 컴퓨터 과학(computer science)과 부울 대수(Boolean algebra)의 문맥에서, $O$ 와 $I$ 는 종종 거짓과 참에 의해 각각 표기되며, 덧셈은 그런-다음 XOR (exclusive or)로 표시되고, 곱셈은 AND로 표시됩니다. 달리 말해서, 이진 필드의 구조는 비트(bit)와 함께 계산하는 것을 허용하는 기본 구조입니다.

Elementary notions

이 섹션에서, $F$ 는 임의의 필드를 나타내고 $a$ 와 $b$ 는 $F$ 의 임의의 원소(elements)입니다.

Consequences of the definition

우리는 $a \cdot 0 = 0$ 와 $- a = (-1) \cdot a$ 를 가집니다.^[7] 특히, 우리는, 우리가 $-1$ 을 알는 순간, 모든 각 원소의 덧셈의 역을 추론할 수 있을 것입니다.

만약 $ab = 0$ 이면, $a$ 또는 $b$ 는 반드시 0이어야 합니다. 사실, 만약 a ≠ 0이면, $0 = a -1 \cdot0 = a -1 (ab) = (a -1 a) b = b$ 입니다. 이것은, 모든 각 필드는 정수 도메인(integral domain)임을 의미합니다.

The additive and the multiplicative group of a field

필드 $F$ 의 공리는 그것이 덧셈 아래의 아벨 그룹(abelian group)임을 의미합니다. 이 그룹은 그 필드의 덧셈의 그룹(additive group)으로 불리고, 그것을 단순히 $F$ 로 표시함으로써 혼동을 줄 수 있을 때, 때때로 $(F, +)$ 로 표시됩니다.

비슷하게, $F$ 의 비-영 원소는 곱셈 아래의 아벨 그룹을 형성하고, 곱셈의 그룹(multiplicative group)으로 불리고, (F \ {0}, ·) 또는 단지 $F \ {0$ } 또는 $F *$ 로 표시됩니다.

필드는, 따라서, $F$ 는 덧셈 아래의 아벨 그룹, $F \ {0$ }는 곱셈 아래의 아벨 그룹 (여기서 0은 덧셈의 항등원입니다), 및 곱셈은 덧셈에 걸쳐 분배적(distributive)임을 만족하는 덧셈과 곱셈으로 나타내는 두 연산을 갖춘, 집합 $F$ 로 정의될 수 있을 것습니다.^{[nb 2]} 필드에 대한 일부 기초 명제는, 그러므로, 그룹(groups)의 일반적인 사실을 적용함으로써 얻어질 수 있습니다. 예를 들어, 덧셈과 곱셈의 역 $- a$ 와 $a -1$ 은 $a$ 에 의해 고유하게 결정됩니다.

요구-사항 $1 \neq 0$ 은 따르는데, 왜냐하면 1은 그룹의 항등원이고 0은 포함되지 않기 때문입니다.^[8] 따라서, 하나의 원소로 구성되는, 자명한 링(trivial ring)은 필드가 아닙니다.

필드의 곱셈의 그룹의 모든 각 유한 부분-그룹은 순환(cyclic)입니다 (Root of unity § Cyclic groups을 참조하십시오.)

Characteristic

F의 두 원소의 곱셈 외에도, 양의 정수 $n$ 에 대해 다음 $n$ -겹 합이 되는 $F$ 의 임의의 원소 $a$ 의 곱 $n \cdot a$ 을 정의하는 것이 가능합니다:

a + a + ... + a

(이것은

F

의 원소입니다.)

만약 다음을 만족하는 양의 정수가 없으면

n \cdot 1 = 0

,

$F$ 는 특성(characteristic) 0을 가진다고 말합니다.^[9] 예를 들어, 유리수 $Q$ 의 필드는 특성 0을 가지는데 왜냐하면 양의 정수 $n$ 은 영이 아니기 때문입니다. 그렇지 않으면, 만약 이 방정식을 만족시키는 양의 정수 $n$ 이 있으면, 가장-작은 그러한 양의 정수는 소수(prime number)로 보일 수 있습니다. 그것은 보통 $p$ 로 표시되고 그 필드는 특성 $p$ 를 가진다고 말합니다. 예를 들어, 필드 $F 4$ 는, 특성 2를 가지는데, 왜냐하면 (위의 덧셈 테이블의 표기법에서) $I + I = O$ 이기 때문입니다.

만약 $F$ 가 특성 $p$ 를 가지면, $F$ 안의 모든 $a$ 에 대해 $p \cdot a = 0$ 입니다. 이것은 다음을 의미합니다:

(a + b) p = a p + b p

,

왜냐하면 이항 공식(binomial formula)에서 보이는 모든 다른 이항 계수(binomial coefficient)는 $p$ 에 의해 나누어질 수 있기 때문입니다. 여기서, $a p := a \cdot a \cdot ... \cdot a$ ( $p$ 인수들)는 $p$ -번째 거듭제곱, 즉, 원소 $a$ 의 $p$ -겹 곱입니다. 그러므로, 프로베니우스 맵(Frobenius map)

Fr: F \to F, x ⟼ x p

은 $F$ 안의 덧셈과 호환되고 (역시 곱셈과 호환되고), 그러므로 필드 준동형입니다.^[10] 이 준동형의 존재는 특성 0의 필드와 꽤 다른 특성 $p$ 의 필드를 만듭니다.

Subfields and prime fields

필드 $F$ 의 부분-필드(subfield) $E$ 는 $F$ 의 필드 연산에 관한 필드인 $F$ 의 부분-집합입니다. 동등하게 $E$ 는 $1$ 을 포함하는 $F$ 의 부분-집합이고, 덧셈, 곱셈, 덧셈의 역 및 비-영 원소의 곱셈의 역 아래에서 닫혀 있습니다. 이것은 $1 ∊ E$ 인 것, 모든 $a, b ∊ E$ 에 대해 $a + b$ 와 $a \cdot b$ 둘 다가 $E$ 안에 있는 것, 및 $E$ 안의 모든 $a \neq 0$ 에 대해 $- a$ 와 $1/ a$ 둘 다가 $E$ 안에 있음을 의미합니다.

필드 준동형(field homomorphism)은 $f (e 1 + e 2) = f (e 1) + f (e 2)$ , $f (e 1 e 2) = f (e 1) f (e 2)$ , 및 $f (1 E) = 1 F$ 를 만족하는 두 필드 사이의 맵 $f : E \to F$ 이며, 여기서 $e 1$ 와 $e 2$ 는 $E$ 의 임의의 원소입니다. 모든 필드 준동형은 단사(injective)입니다.^[11] 만약 $f$ 가 역시 전사(surjective)이면, 그것은 동형-사상(isomorphism)으로 불립니다 (또는 필드 $E$ 와 $F$ 는 동형적이라고 불립니다).

필드는, 만약 그것이 적절한 (즉, 엄격하게 더 작은) 부분-필드를 가지지 않으면, 소수 필드(prime field)로 불립니다. 임의의 필드 $F$ 는 소수 필드를 포함합니다. 만약 $F$ 의 특성이 $p$ (소수)이면, 소수 필드는 아래에 도입된 유한 필드 $F p$ 에 동형적입니다. 그렇지 않으면, 소수 필드는 $Q$ 에 동형적입니다.^[12]

Finite fields

유한 필드(Finite fields) (갈루아 필드(Galois fields)라고 역시 불림)는 유한하게 많은 원소를 갖는 필드로, 그 숫자는 필드의 차수로 역시 참조됩니다. 위의 입문 예제 $F 4$ 는 네 원소를 갖는 필드입니다. 그의 부분-필드 $F 2$ 는 가장 작은 필드인데, 왜냐하면 정의에 따라 필드는 적어도 두 구별되는 원소 $1 \neq 0$ 를 가지기 때문입니다.

소수 차수를 갖는, 가장-간단한 유한 필드는 모듈러 산술(modular arithmetic)을 사용하여 가장 직접적으로 접근-가능합니다. 고정된 양의 정수 n에 대해, 산술 "모듈로 $n$ "은 다음 숫자와 함께 동작하는 것을 의미합니다:

Z / n Z = {0, 1, ..., n - 1}.

이 집합 위의 덧셈과 곱셈은 정수의 집합 $Z$ 에서 $n$ 으로 나누고 결과로 나머지를 취함으로써 문제에서 연산을 수행함으로써 행해집니다. 이 구성은, 만약 $n$ 이 소수(prime number)이면, 정확하게 필드를 산출합니다. 예를 들어, 소수 $n = 2$ 를 취하면 위에-언급된 필드 $F 2$ 가 결과로써 생깁니다. $n = 4$ 및 보다 일반적인 것에 대해, 임의의 합성수(composite number) (즉, 두 개의 엄격히 작은 자연수의 곱 $n = r \cdot s$ 으로 표현될 수 있는 임의의 숫자 $n$ )에 대해, $Z / n Z$ 는 필드가 아닙니다: 두 비-영 원소의 곱은 영인데 왜냐하면 $Z / n Z$ 에서 $r \cdot s = 0$ 이기 때문으로, 이것은, 위에서 표현한 것처럼, $Z / n Z$ 가 필드가 되는 것을 막습니다. 이런 방식으로 구성된 ( $p$ 가 소수인) $p$ 원소를 갖는 필드 $Z / p Z$ 는 보통 $F p$ 로 표시됩니다.

모든 각 유한 필드 $F$ 는 $q = p n$ 원소를 가지며, 여기서 $p$ 는 소수이고 $n \geq 1$ 입니다. 이 명제는 유지되는데 왜냐하면 $F$ 는 그의 소수 필드에 걸쳐 벡터 공간으로 보일 수 있을 것이기 때문입니다. 이 벡터 공간(vector space)의 차원(dimension)은 필연적으로 유한이며, 말하자면 $n$ , 이것은 단언한 명제를 의미합니다.^[13]

$q = p n$ 원소를 갖는 필드는 다음 다항식의 분해 필드(splitting field:분해체)로 구성될 수 있습니다:

f (x) = x q - x

.

그러한 분해 필드는 다항식 $f$ 가 $q$ 영들을 가지는 $F p$ 의 확장입니다. 이것은 $f$ 가 가능한 한 많은 영들을 가짐을 의미하는데 왜냐하면 $f$ 의 차수(degree)가 $q$ 이기 때문입니다. $q = 2 2 = 4$ 에 대해, 그것은 $F 4$ 의 모든 네 원소가 방정식 $x 4 = x$ 를 만족시키는, 그래서 그들은 $f$ 의 영인 것을 위의 곱셈 테이블을 사용하여 경우마다 검사할 수 있습니다. 대조적으로, $F 2$ 에서, $f$ 는 단지 두 개의 영들 (즉, 0과 1)을 가지므로, $f$ 는 이 더 작은 필드에서 선형 인수로 분리되지 않습니다. 기본적인 필드-이론적 개념 위에 더 나아가서 설명하면, 같은 차수를 갖는 두 개의 유한 필드가 동형임을 보여줄 수 있습니다.^[14] 그것은, 따라서, $F q$ 또는 $GF(q)$ 로 표시되는, $q$ 원소를 갖는 그 유한 필드에 대해 말하는 것이 관례적입니다.

History

역사적으로, 세 개의 대수적 분야는 필드의 개념을 이끌었습니다: 그것은 다항 방정식을 푸는 질문, 대수적 숫자 이론(algebraic number theory), 및 대수 기하학(algebraic geometry)입니다.^[15] 필드의 개념을 향한 첫 번째 단계는 1770년에 조제프-루이 라그랑주(Joseph-Louis Lagrange)에 의해 만들어졌으며, 그는 (단위의 세 번째 근(third root of unity) $ω$ 를 갖는) 다음 표현

(x 1 + ω x 2 + ω 2 x 3) 3

에서 삼차 다항식(cubic polynomial)의 영들 $x 1, x 2, x 3$ 을 순열화함으로써 두 값을 오직 산출한다는 것을 관찰했습니다. 미지수 $x$ 에 대해 삼차 방정식을 $x 3$ 에 대한 이차 방정식으로 줄임으로써 진행되는, 이 방법으로, 리그랑주는 시피오니 델 페로(Scipione del Ferro)와 프랑수아 비에트(François Viète)의 고전적 해결 방법을 개념적으로 설명했습니다.^[16] 사차 방정식(equation of degree 4)에 대해 비슷한 관찰과 함께, 라그랑주는 따라서 결국 필드의 개념과 그룹의 개념이 되는 무엇을 연결했습니다.^[17] 방데르몽드(Vandermonde)는, 역시 1770년에, 및 더 완전한 확장까지, 카를 프리드리히 가우스(Carl Friedrich Gauss)는 그의 책 Disquisitiones Arithmeticae (1801)에서, 소수 $p$ 에 대해, 방정식

x p = 1

을 연구했고, 다시 현대 언어를 사용하여, 결과로써 생기는 순환 갈루아 그룹(Galois group)을 연구했습니다. 가우스는 정규 $p$ -다각형(regular $p$ -gon:정 $p$ -각형)은, 만약 $p = 2 2 k + 1$ 이면, 구성될 수 있음을 추론했습니다. 라그랑주의 연구를 바탕으로, 파올로 루피니(Paolo Ruffini)는 (차수 5의 다항 방정식) 오차 방정식(quintic equation)은 대수적으로 풀 수는 없다는 것 (1799)을 주장했지만, 어쨌든 그의 논증은 결함이 있습니다. 이들 틈은 닐스 헨리크 아벨(Niels Henrik Abel)에 의해 1824년에 채워졌습니다.^[18] 에바리스트 갈루아(Évariste Galois)는, 1832년에, 대수적으로 풀 수 있는 다항식 방정식에 대해 필요 및 충분한 기준을 고안했으며, 따라서 오늘날 갈루아 이론(Galois theory)으로 알려진 것을 효과적으로 확립했습니다. 아벨과 갈루아 둘 다는 오늘날 대수적 숫자 필드(algebraic number field)라고 불리는 것으로 연구했지만, 필드 또는 그룹 모두의 명시적인 개념을 생각하지 않았습니다.

1871년 리하르트 데데킨트(Richard Dedekind)는, 네 가지 산술 연산 아래에서 닫힌 실수 또는 복소수 집합에 대해, (유기적으로 닫힌 실재를 제안하기 위해) "몸" 또는 "신체"를 의미하는, 독일(German) 단어 Körper를 도입했습니다. 영어 용어 "필드"는 Moore (1893)에 의해 도입되었습니다.^[19]

필드에 의해 우리는 실수 또는 복소수의 모든 각 무한 시스템은 그 자체로 및 완전하게 닫혀 있으므로 이들 숫자의 임의의 두 개의 덧셈, 뺄셈, 곱셈 및 나눗셈이 시스템의 숫자를 다시 생성함을 의미할 것입니다.
— Richard Dedekind, 1871^[20]

1881년 레오폴트 크로네커(Leopold Kronecker)는, 현대 용어에서 유리 분수(rational fraction)의 필드인, 유리성의 도메인(domain of rationality)으로 불리는 것을 정의했습니다. 크로네커의 개념은 (데데킨트의 의미에서의 필드인) 모든 대수적 숫자의 필드를 덮지는 못했지만, 다른 한편으로 데데킨트의 개념보다 더 추상적이었으며 그것에서 그것은 필드의 원소의 본질에 대한 특유한 가정을 만들지 않았습니다. 크로네커는 $Q (π)$ 와 같은 필드를 추상적으로 유리 함수 필드 $Q (X)$ 로 해석했습니다. 이것 이전에, 초월적 숫자의 예제는, 1844년에 조제프 리우빌(Joseph Liouville)의 연구 이후, 샤를 에르미트(Charles Hermite) (1873)와 페르디난트 폰 린데만(Ferdinand von Lindemann) (1882)이, 각각, $e$ 와 $π$ 의 초월성을 증명할 때까지, 알려졌습니다.^[21]

추상적 필드의 첫 번째 명확한 정의는 Weber (1893)에 의한 것입니다.^[22] 특히, 하인리히 마르틴 베버(Heinrich Martin Weber)의 개념은 필드 F_p를 포함했습니다. 주세페 베로네세(Giuseppe Veronese) (1891)는, Hensel (1904)에 의해 p-진수 숫자의 필드를 도입하기 위해 선도하는, 형식적 거듭제곱 급수의 필드를 연구했습니다. Steinitz (1910)는 여태까지 축적된 추상적 필드 이론의 지식을 종합했습니다. 그는 필드의 속성을 공리적으로 연구했고 많은 중요한 필드-이론적 개념을 정의했습니다. 섹션 갈로아 이론(Galois theory)에서 언급된 정리의 대부분은, 필드를 구성하는 것(Constructing fields) 및 초등 개념(Elementary notions)은 슈타이니츠의 연구에서 찾을 수 있습니다. Artin & Schreier (1927)은 필드에서 순서화(ordering in a field)의 개념, 따라서 해석학의 영역을 순수한 대수적 속성에 연결시켰습니다.^[23] 에밀 아르틴(Emil Artin)은 1928년에서 1942년까지 갈루아 이론을 재개발하여, 원시 원소 정리(primitive element theorem)에 대한 의존성을 제거했습니다.

Constructing fields

Constructing fields from rings

교환 링(commutative ring)은, 곱셈 역 $a -1$ 의 존재를 제외하고는, 필드의 모든 공리를 만족시키는, 덧셈 및 곱셈 연산을 갖춘, 집합입니다.^[24] 예를 들어, 정수 $Z$ 는 교환 링을 형성하지만, 필드는 아닙니다: 정수 $n$ 의 역수(reciprocal)는, 만약 $n = \pm1$ 이 아니면, 정수 자체가 아닙니다.

대수적 구조의 계층에서, 필드는 모든 각 비-영 원소가 단위(unit)인 교환 링 $R$ 로 특성화될 수 있습니다 (이것은 모든 각 원소가 역이 가능함을 의미합니다). 비슷하게, 필드는 정확하게 두 구별되는 아이디얼(ideal), $(0)$ 과 $R$ 을 갖는 교환 링입니다. 필드는 $(0)$ 이 유일한 소수 아이디얼(prime ideal)인 역시 정확하게 교환 링입니다.

교환 링 $R$ 이 주어지면, $R$ 과 관련된 필드를 구성하는 두 방법, 즉, 모든 비-영 원소가 역-가능이 되도록 $R$ 을 수정하는 두 가지 방법: 분수 필드를 형성하는 것, 및 나머지 필드를 형성하는 것의 두 방법이 있습니다. $Z$ 의 분수의 필드는 $Q$ , 유리수이며, 반면에 $Z$ 의 나머지 필드는 유한 필드 $F p$ 입니다.

Field of fractions

정수 도메인(integral domain) $R$ 이 주어지면, 그의 분수의 필드(field of fractions) $Q (R)$ 은 Q는 정수로부터 구성되는 정확하게 $R$ 의 두 원소의 분수로 세워집니다. 보다 정확하게, $Q (R)$ 의 원소는, $a$ 와 $b$ 가 $R$ 안에 있고, $b \neq 0$ 인, 분수 $a / b$ 입니다. 두 분수 $a / b$ 와 $c / d$ 가 같은 것과 $ad = bc$ 인 것은 필요충분 조건입니다. 분수 위의 연산은 유리수에 대한 것만큼 정확하게 작동합니다. 예를 들어,

{\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}.

만약 링이 정수 도메인이면, 분수의 집합이 필드를 형성함을 보이는 것은 복잡하지 않습니다.^[25]

필드 (또는 정수 도메인) $F$ 에 걸쳐 유리 분수(rational fraction)의 필드 $F (x)$ 는 다항식 링(polynomial ring) $F [x]$ 의 분수의 필드입니다. 필드 $F$ 에 걸쳐 로랑 급수(Laurent series)

\sum _{i=k}^{\infty }a_{i}x^{i}\ (k\in \mathbb {Z} ,a_{i}\in F)

의 필드 $F ((x))$ 는 ( $k \geq 0$ 에서) 형식적 거듭제곱 급수(formal power series)의 링 $F [[x]]$ 의 분수의 필드입니다. 로랑 급수는 (임의의 거듭제곱 급수와는 대조적으로) $x$ 의 거듭제곱으로 나눈 거듭제곱 급수의 분수이므로, 분수의 표현은, 그래도, 이 상황에서 덜 중요합니다.

Residue fields

$R$ 을 단사적으로(injectively) 필드로 삽입하는, 분수의 필드 외에도, 필드는 필드 $F$ 위로 전사적인 맵(surjective map)을 수단으로 교환 링 $R$ 로부터 얻어질 수 있습니다. 이런 방법으로 얻어진 필드는 몫(quotient) $R / m$ 이며, 여기서 $m$ 은 $R$ 의 최대 아이디얼(maximal ideal)입니다. 만약 $R$ 이 오직 하나의 최대 아이디얼 $m$ 을 가지면, 이 필드는 $R$ 의 잔여 필드(residue field)로 불립니다.^[26]

(필드 E에 걸쳐) 다항식 링 $R = E [X]$ 안의 하나의 다항식 $f$ 에 의해 생성된 아이디얼이 극대인 것과 $f$ 가 $E$ 안의 기약인 것, 즉, $f$ 가 더 작은 차수(degree)의 $E [X]$ 에서 두 다항식의 곱으로 절대 표현될 수 없는 것은 필요충분 조건입니다. 이것은 다음 필드를 산출합니다:

F = E [X] / (p (X)).

이 필드 $F$ 는 다음 방정식을 만족시키는 원소 $x$ (즉, $X$ 의 잔여 클래스(residue class))를 포함합니다:

f (x) = 0

.

예를 들어, $C$ 는, $f (X) = X 2 + 1$ 인, $f (i) = 0$ 을 만족시키는 허수 단위(imaginary unit) 기호 i에 인접(adjoining)함으로써 $R$ 로부터 얻습니다. 게다가, $f$ 는 $R$ 에 걸쳐 기약이며, 이것은 다항식 $f (X) ∊ R [X]$ 를 $f (i)$ 로 보내는 맵이 다음 동형-사상을 산출한다는 것을 의미합니다:

\mathbf {R} [X]/\left(X^{2}+1\right)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbf {C} .

Constructing fields within a bigger field

필드는 주어진 더 큰 컨테이너 필드 안에 구성될 수 있습니다. 필드 $E$ , 및 부분-필드로 $E$ 를 포함하는 필드 $F$ 가 주어졌다고 가정합니다. $F$ 의 임의의 원소 $x$ 에 대해, $x$ 에 의해 생성된 F의 부분-필드로 불리고 $E (x)$ 로 표시되는, $E$ 와 $x$ 를 포함하는 $F$ 의 가장 작은 부분-필드가 있습니다.^[27] $E$ 에서 $E (x)$ 로의 통로는 원소를 E에 인접(adjoining)함으로써 참조됩니다. 보다 일반적으로, 부분-집합 $S \subset F$ 에 대해, $E (S)$ 로 표시되는, $E$ 와 $S$ 를 포함하는 $F$ 의 최소의 부분-필드가 있습니다.

어떤 필드 $F$ 의 두 부분-필드 $E$ 와 $E'$ 의 합성-필드(compositum)는 $E$ 및 $E'$ 둘 다를 포함하는 $F$ 의 가장-작은 부분-필드입니다. 합성-필드는, 아래 소개된 언어에서, 예를 들어, $E$ 에 걸쳐 대수적인, $F$ 의 가장-큰 부분-필드와 같은, 어떤 속성을 만족시키는 $F$ 의 가장-큰 부분-필드를 구성하기 위해 사용될 수 있습니다.^{[nb 3]}

Field extensions

부분-필드 $E \subset F$ 의 개념은, 다음

F / E

으로 표시되고 " $E$ 에 걸쳐 $F$ "로 읽는, $F$ 가 $E$ 의 필드 확장(field extension) (또는 단지 확장)인 것을 참조함으로써, 반대 관점으로부터 역시 고려될 수 있습니다.

필드 확장의 기본 자료는 그의 차수(degree) $[F : E]$ , 즉, $E$ -벡터 공간으로 $F$ 의 차원입니다. 그것은 다음 공식을 만족시킵니다:^[28]

[G : E] = [G : F] [F : E]

.

그의 차수가 유한한 확장은 유한 확장으로 참조됩니다. 확장 $C / R$ 및 $F 4 / F 2$ 는 차수 2이고, 반면에 $R / Q$ 은 무한 확장입니다.

Algebraic extensions

필드 확장 $F / E$ 의 연구에서 중추적인 개념은 대수적 원소(algebraic element)입니다. 원소 $x\in F$ 는, 만약 그것이 $E$ 에서 계수를 갖는 다항식(polynomial)의 근(root)이면, 즉, 만약 그것이 $e n \neq 0$ 이고, $E$ 에서 $e n, ..., e 0$ 을 갖는 다항 방정식(polynomial equation)

e n x n + e n -1 x n -1 + \cdot\cdot\cdot + e 1 x + e 0 = 0

을 만족시키면, $E$ 에 걸쳐 대수적입니다. 예를 들어, $C$ 안의 허수 단위(imaginary unit) $i$ 는 $R$ , 심지어 $Q$ 에 걸쳐 대수적인데, 왜냐하면 그것은 다음 방정식을 만족시킵니다:

i 2 + 1 = 0

.

$F$ 의 모든 각 원소가 $E$ 에 걸쳐 대수적인 필드 확장은 대수적 확장(algebraic extension)으로 불립니다. 임의의 유한 확장은 반드시 대수적인데, 왜냐하면 위의 곱셈-가능성 공식으로부터 추론될 수 있기 때문입니다.^[29]

원소 $x$ 에 의해 생성된 부분-필드 $E (x)$ 는, 위에서 처럼, $E$ 의 대수적 확장인 것과 $x$ 가 대수적 원소인 것은 필요충분 조건입니다. 즉 말하자면, 만약 $x$ 가 대수적이면, $E (x)$ 의 모든 다른 원소는 마찬가지로 반드시 대수적이어야 합니다. 게다가, 확장 $E (x) / E$ 의 차수, 즉, $E$ -벡터 공간으로 $E (x)$ 의 차원은, 위에서 처럼, $x$ 를 포함하는 다항 방정식이 있는 것을 만족하는 최소 차수 $n$ 과 같습니다. 만약 이 차수가 $n$ 이면, $E (x)$ 의 원소는 다음 형식을 가집니다:

\sum _{k=0}^{n-1}a_{k}x^{k},\ \ a_{k}\in E.

예를 들어, 가우스 유리수(Gaussian rational)의 필드 $Q (i)$ 는 $a$ 와 $b$ 모두가 유리수인 형식 $a + bi$ 의 모든 숫자로 구성되는 $C$ 의 부분-필드입니다: 형식 $i 2$ (그리고 비슷하게 더 높은 지수에 대해)의 합해지는 숫자는 여기서 고려될 필요가 없는데, 왜냐하면 $a + bi + ci 2$ 는 $a - c + bi$ 로 단순화될 수 있기 때문입니다.

Transcendence bases

$X$ 가 불확정(indeterminate)인, 유리 분수(rational fraction) $E (X)$ 의 위에서-언급된 필드는 $E$ 의 대수적 확장이 아닌데 왜냐하면 그의 영이 $X$ 인 $E$ 안의 계수를 갖는 다항 방정식이 없기 때문입니다. $X$ 와 같은, 대수적이지 않은 원소는 초월적(transcendental)으로 불립니다. 비공식적으로 말하자면, 불확정 $X$ 와 그의 거듭제곱은 $E$ 의 원소와 상호-작용하지 않습니다. 비슷한 구성은, 단지 일(1) 대신에, 불확정성의 집합과 함께 수행될 수 있습니다.

다시 한번, 위에서 논의된 필드 확장 $E (x) / E$ 는 핵심 예제입니다: 만약 $x$ 가 대수적이지 않으면 (즉, $x$ 는 $E$ 안의 계수를 갖는 다항식의 근(root)이 아닙니다), $E (x)$ 는 $E (X)$ 와 동형입니다. 이 동형은 유리 분수에서 $x$ 를 $X$ 로 대체함으로써 얻어질 수 있습니다.

필드 $F$ 의 부분-집합 $S$ 는, 만약 그것이 $E$ 에 걸쳐 대수적으로 독립(algebraically independent)이면 (임의의 다항 관계를 만족시키지 못합니다) 및 만약 $F$ 가 $E (S)$ 의 대수적 확장이면, 초월 기저(transcendence basis)입니다. 임의의 필드 확장 $F / E$ 는 초월 기저를 가집니다.^[30] 따라서, 필드 확장은 형식 $E (S) / E$ (순수하게 초월적 확장)의 하나 및 대수적 확장으로 분리될 수 있습니다.

Closure operations

필드는, 만약 그것이 엄격하게 더 큰 대수적 확장을 가지지 않으면, 또는 동등하게, 만약 임의의 다항 방정식(polynomial equation)

f n x n + f n -1 x n -1 + \cdot\cdot\cdot + f 1 x + f 0 = 0

, 여기서 계수(coefficients)

f n, ..., f 0 \in F, n > 0

이 하나의 해 $x ∊ F$ 를 가지면, 대수적으로 닫혀 있습니다.^[31] 대수학의 기본 정리(fundamental theorem of algebra)에 의해, $C$ 는 대수적으로 닫혀 있습니다, 즉, 복소수 계수를 갖는 임의의 다항 방정식은 하나의 복소수 해를 가집니다. 유리수 및 실수는 대수적으로 닫혀 있지 않습니다. 왜냐하면 방정식

x 2 + 1 = 0

은 임의의 유리수 또는 실수 해를 가지지 않습니다. $F$ 를 포함하는 필드는, 만약 그것이 (대략 말해서, $F$ 에 비해서 너무 크지 않은) $F$ 에 걸쳐 대수적이면 및 (모든 다항식 방정식의 해를 포함하기에 충분하게 큰) 대수적으로 닫혀 있으면, 대수적 클러저(algebraic closure)로 불립니다.

위에 위해, $C$ 는 $R$ 의 대수적 클로저입니다. 대수적 클로저가 필드 $F$ 의 유한 확장인 상황은 꽤 특별합니다: 아르틴-슈라이어 정리(Artin-Schreier theorem)에 의해, 이 확장의 차수는 반드시 2이고, $F$ 는 $R$ 에 기초적으로 동치(elementarily equivalent)입니다. 그러한 필드는 실수 닫힌 필드(real closed field)로 역시 알려져 있습니다.

임의의 필드 $F$ 는 대수적 클로저를 가지며, 이것은 (비-고유한) 동형-사상까지(up to) 그 위에 고유합니다. 그것은 공통적으로 그 대수적 클로저로 참조되고 F로 표시됩니다. 예를 들어, $Q$ 의 대수적 클로저 $Q$ 는 대수적 숫자(algebraic number)의 필드로 불립니다. 필드 F는 보통 꽤 함축적인데, 왜냐하면 그것의 구성이 극단-필터 보조정리(ultrafilter lemma), 선택의 공리(axiom of choice)보다 더-약한 집합-이론적 공리를 요구하기 때문입니다.^[32] 이와 관련하여, $F q$ 의 대수적 클로저는 예외적으로 간단합니다. 그것은 $F q$ (차수 $q n$ 의 필드들)를 포함하는 유한 필드의 합집합입니다. 특성 0의 임의의 대수적으로 닫힌 필드 $F$ 에 대해, 로랑 급수(Laurent series)의 필드 $F ((t))$ 의 대수적 클로저는, $t$ 의 인접한 근에 의해 얻어진, 퓌죄 급수(Puiseux series)의 필드입니다.^[33]

Fields with additional structure

필드는 수학과 그 이상에서 보편적이므로, 개념의 여러 정제가 특정 수학 영역의 필요에 맞게 조정되어 왔습니다.

Ordered fields

필드 F가, 만약 $x \geq 0$ 와 $y \geq 0$ 일 때마다 $x + y \geq 0$ 와 $xy \geq 0$ 가 되도록 임의의 두 원소가 비교되면, 순서화 필드(ordered field)로 불립니다. 예를 들어, 실수는 보통 순서화 ≥와 함께, 순서화 필드를 형성합니다. 아르틴-슈라이어 정리(Artin-Schreier theorem)는 필드가 순서화될 수 있는 것과 그것이 형식적 실수 필드(formally real field:형식적 실체)이며, 이것은 임의의 이차 방정식

x_{1}^{2}+x_{2}^{2}+\dots +x_{n}^{2}=0

은 오직 해 $x 1 = x 2 = ... = x n = 0$ 를 가지는 것은 필요충분 조건이라는 것을 말합니다.^[34] 고정된 필드 F 위의 모든 가능한 순서의 집합은 F에 걸쳐 이차 형식(quadratic form)의 비트 링(Witt ring) W(F)에서, Z까지의 링 준동형(ring homomorphism)의 집합에 동형입니다.^[35]

아르키메데스 필드(Archimedean field)는, 각 원소에 대해, 그의 값이 해당 원소보다 더 큰, 즉, 무한한 원소가 없는, 유한 표현

1 + 1 + ··· + 1

이 존재하는 것을 만족하는 순서화 필드입니다. 동등하게, 그 필드는 (모든 유리수보다 더 작은 원소) 무한소(infinitesimals)를 포함하지 않습니다; 또는, 여전히 동등하게, 그 필드는 $R$ 의 부분-필드와 동형입니다.

순서화 필드는, 만약 모든 위쪽 경계(upper bound), 아래쪽 경계(lower bound) (데데킨트 자름(Dedekind cut)을 참조하십시오) 및, 극한, 반드시 존재해야 하는, 존재하면, 데데킨트-완비(Dedekind-complete)입니다. 보다 공식적으로, $F$ 의 각 경계진 부분-집합(bounded subset)은 적어도 위쪽 경계를 가져야 합니다. 임의의 완비 필드는 반드시 아르키메데스 필드인데,^[36] 왜냐하면 임의의 비-아르키메데스 필드에서 가장-큰 무한소도 아니고 최소 양의 유리수도 없으며, 수열 $1/2, 1/3, 1/4, \dots$ 로부터, 모든 각 무한소보다 더-큰 모든 각 원소가 극한을 가지지 않기 때문입니다.

실수의 모든 각 적절한 부분-필드는 역시 그러한 틈을 포함하므로, $R$ 은, 동형까지(up to), 고유한 완비 순서화 필드입니다.^[37] 미적분학(calculus)에서 여러 기초적인 결과는 실수의 이 특성으로부터 직접 따릅니다.

초실수(hyperreals) $R *$ 는 아르키메데스가 아닌 순서화 필드를 형성합니다. 그것은 무한한 및 무한소 숫자를 포함함으로써 얻어진 실수의 확장입니다. 이들은 더 크고, 임의의 실수보다 각각 더 작습니다. 초실수는 비-표준 해석학(non-standard analysis)의 기초적인 기저를 형성합니다.

Topological fields

필드의 개념의 또 다른 정제는, 필드의 모든 연산 (덧셈, 곱셈, 맵 $a \mapsto - a$ 및 $a \mapsto a -1$ )은 공간의 토폴로지에 관한 연속적인 맵(continuous map)을 만족하는, 집합 F가 토폴로지적 공간(topological space)인, 토폴로지적 필드(topological field)입니다.^[38] 아래에서 논의된 모든 필드의 토폴로지는 메트릭(metric), 즉, $F$ 의 임의의 두 원소 사이의 거리를 측정하는 함수

d : F \times F \to R

로부터 유도됩니다.

$F$ 의 완비(completion)는, 비공식적으로 말하면, 원래 필드 $F$ 안의 "틈"이 채워지는, 만약 임의의 것이 있으면, 또 다른 필드입니다. 예를 들어, $x = \sqrt 2$ 와 같은, 임의의 무리수(irrational number) $x$ 는, 절댓값(absolute value) $| x - p / q |$ 에 의해 주어진 $x$ 와 $p / q$ 의 거리가 원하는 만큼 작아지는 의미에서, 그것이 유리수 $p / q$ 에 의해 임의적으로 가깝게 근사화될 수 있는 실수라는 의미에서, 유리수 $Q$ 에서 "갈라진 틈"입니다. 다음 테이블은 이 구성의 일부 예제를 나열합니다. 네 번째 열은 영 수열(sequence), 즉, ( $n \to \infty$ 에 대해) 그의 극한이 영인 수열의 예제를 보여줍니다.

필드(Field)	메트릭(Metric)	완비(Completion)	영 수열(zero sequence)
$Q$	$\| x - y \|$ (보통 절댓값)	R	$1/ n$
$Q$	소수 $p$ 에 대해, p-진수 평가를 사용하여 획득된	$Q p$ $p$ -진수 숫자	$p n$
$F (t)$ ( $F$ any field)	$t$ -진수 평가를 사용하여 획득된	$F ((t))$	$t n$

필드 $Q p$ 는 숫자 이론 및 $p$ -진수 해석학( $p$ -adic analysis)에서 사용됩니다. 대수적 클로저 $Q p$ 는 $Q p$ 위의 하나를 확장하는 고유한 노름을 전달하지만, 완비는 아닙니다. 이 대수적 클로저의 완비는, 어쨌든, 대수적으로 닫힙니다. 복소수에 대한 그의 대략 유사때문에, 그것은 때때로 메트릭 완비 및 대수적 클로저 복소수 p-진수 숫자(complex p-adic number)의 필드로 불리고 $C p$ 에 의해 표시됩니다.^[39]

Local fields

다음 토폴로지적 필드는 지역 필드(local field)로 불립니다:^[40]^{[nb 4]}

$Q p$ 의 유한 확장 (특성 영의 지역 필드)
$F p ((t))$ 의 유한 확장, $F p$ 에 걸쳐 로랑 급수의 필드 (특성 $p$ 의 지역 필드).

지역 필드의 이들 두 유형은 일부 근본적인 유사점을 공유합니다. 이 관계에서, (균일화자(uniformizer)로 참조되는) 원소 $p \in Q p$ 및 $t \in F p ((t))$ 는 서로 일치합니다. 이것의 첫 번째 표명은 초등 수준에 있습니다: 두 필드의 원소는, $F p$ 안의 계수를 갖는, 균일화자에서 거듭제곱 급수로 표현될 수 있습니다. (어쨌든, $Q p$ 의 덧셈은, $F p ((t))$ 안의 경우가 아닌, 캐리(carry:받아올림)를 사용하여 이루어지기 때문에, 이들 필드는 동형이 아닙니다.) 다음의 사실은 이 피상적 닮음이 훨씬 더 깊어진다는 것을 보여줍니다:

거의 모든 $Q p$ 에 대해 참인 임의의 일-차(first order) 명제는 거의 모든 $F p ((t))$ 에서 역시 참입니다. 이것의 응용은 $Q p$ 에서 동차 다항식의 영을 묘사하는 액스-코흔 정리(Ax-Kochen theorem)입니다.
두 필드 모두의 무분별하게 분열된 확장이 서로에게 전단사입니다.
( $F p ((t))$ 안의) $t$ 의 각각의, ( $Q p$ 안의) $p$ 의 임의의 $p$ -거듭제곱 근을 인접시키면, 퍼펙토이드 필드(perfectoid field)로 알려진 이들 필드의 (무한한) 확장을 산출합니다. 눈에 띄게, 이들 두 필드의 갈루아 그룹은 동형이고, 이것은 이들 두 필드 사이에 현저한 평행을 처음으로 엿볼 수 있습니다:^[41]

\operatorname {Gal} \left(\mathbf {Q} _{p}\left(p^{1/p^{\infty }}\right)\right)\cong \operatorname {Gal} \left(\mathbf {F} _{p}((t))\left(t^{1/p^{\infty }}\right)\right).

Differential fields

미분 필드(differential field_는 도함수(derivation)를 갖춘 필드이며, 즉, 필드 안의 원소의 도함수를 취하는 것을 허용합니다.^[42] 예를 들어, 다항식의 표준 도함수와 함께 필드 R(X)는 미분 필드를 형성합니다. 이들 필드는 미분 갈루아 이론(differential Galois theory), 선형 미분 방정식(linear differential equation)을 다루는 갈루아 이론의 변형에서 핵심입니다.

Galois theory

갈루아 이론은 덧셈과 곱셈의 산술 연산에서 대칭(symmetry)을 연구함으로써 필드의 대수적 확장(algebraic extension)을 연구합니다. 이 영역에서 중요한 개념은 유한(finite) 갈루아 확장(Galois extension) $F / E$ 이며, 이것은, 정의에 의해, 분해-가능(separable)이고 정규(normal)인 것들입니다. 원시 원소 정리(primitive element theorem)는 유한 분해-가능한 확장이 반드시 단순(simple)이고, 즉, 형태

F = E [X] / f (X)

임을 보여주며, 여기서 $f$ 는 (위에서 처럼) 기약 다항식입니다.^[43] 그러한 확장에 대해, 정규 및 분해 가능인 것은 $f$ 의 모든 영들이 $F$ 에 포함되고 $f$ 가 오직 단순 영들을 가짐을 의미합니다. 후자의 조건은, 만약 $E$ 가 특성 0을 가지면, 항상 충족됩니다.

유한 갈루아 확장에 대해, 갈루아 그룹(Galois group) $Gal(F / E)$ 는 $E$ 위의 자명한 $F$ 의 필드 자기-동형(field automorphism) (즉, 덧셈과 곱셈을 보존하고 $E$ 의 원소를 그들 자신에게 보내는 전단사(bijection) $σ : F \to F$ )의 그룹입니다. 이 그룹의 중요성은 $Gal(F / E)$ 의 부분-그룹(subgroup)의 집합과 확장 $F / E$ 의 중간 확장의 집합 사이의 명시적 일-대-일 대응(one-to-one correspondence)을 구성하는, 갈루아 이론의 기본 정리(fundamental theorem of Galois theory)에서 유래합니다.^[44] 이 대응을 수단으로, 그룹-이론적 속성은 필드에 대한 사실로 변환합니다. 예를 들어, 만약 위와 같은 갈루아 확장의 갈루아 그룹은 풀 수 있는(solvable) 그룹이 아니면 (아벨 그룹(abelian group)에서 절대 구축될 수 없습니다), $f$ 의 영들은 덧셈, 곱셈, 및 제곱근, 즉, ${\sqrt[{n}]{\ }}$ 를 포함하는 표현의 관점에서 절대 표현될 수 없습니다. 예를 들어, 대칭 그룹(symmetric group) $S n$ 은 $n \geq5$ 에 대해 풀 수 없습니다. 결과적으로, 보일 수 있는 것처럼, 다음 다항식의 영들은 합, 곱, 및 제곱근에 의해 표현-가능하지 않습니다. 후자의 다항식에 대해, 이 사실은 아벨–루피니 정리(Abel–Ruffini theorem)로 알려져 있습니다:

f (X) = X 5 - 4 X + 2

(and

E = Q

),^[45]

f (X) = X n + a n -1 X n -1 + ... + a 0

(여기서

f

는, 어떤 불확정

a i

,

E

는 임의의 필드, 및

n \geq 5

에 대해,

E (a 0, ..., a n -1)

에서 방정식으로 여겨집니다).

필드의 텐서 곱(tensor product of fields)은 보통 필드가 아닙니다. 예를 들어, 차수 $n$ 의 유한 확장 $F / E$ 가 갈루아 확장인 것과 다음 F-대수의 동형이 있는 것은 필요충분 조건입니다:

F \otimes E F ≅ F n

.

이 사실은, 그로텐디크의 갈루아 이론(Grothendieck's Galois theory), 대수-기하적 대상에 적용할 수 있는 갈루아 이론의 광범위한 확장의 시작입니다.^[46]

Invariants of fields

필드 $F$ 의 기본 불변은 그의 소수 필드에 걸쳐 $F$ 의 특성과 초월 차수(transcendence degree)를 포함합니다. 후자는 소수 필드에 걸쳐 대수적으로 독립적인 $F$ 안의 원소의 최대 숫자로 정의됩니다. 두 대수적으로 닫힌 필드 $E$ 와 $F$ 는, 만약 이들 두 데이터가 일치하면, 정확하게 동형입니다.^[47] 이것은 같은 카디널리티(cardinality) 및 같은 특성의 임의의 두 셀-수-없는(uncountable) 대수적으로 닫힌 필드가 동형임을 의미합니다. 예를 들어, $Q p, C p$ 및 $C$ 는 동형입니다 (그러나 토폴로지적 필드로 동형은 아닙니다).

Model theory of fields

수학적 논리(mathematical logic)의 한 가지, 모델 이론(model theory)에서, 두 필드 $E$ 와 $F$ 는, 만약 $E$ 에 대해 참인 모든 각 수학적 명제가 $F$ 에 대해 역시 참이고 그 역도 참이면, 기본 동치(elementarily equivalent)로 불립니다. 문제에서 수학적 명제가 (0, 1, 덧셈 및 곱셈을 포함하는) 일-차(first-order) 문장이 되는 것이 요구됩니다. 전형적인 예제는 다음입니다:

φ(E)

= "임의의

n > 0

에 대해,

E

안의 차수

n

의 임의의 다항식은

E

안의 영을 가집니다" (이것은

E

가 대수적으로 닫힘을 전체적으로 말하는 것입니다).

렙셰츠 원리(Lefschetz principle)는 $C$ 가 특성 영의 임의의 대수적으로 닫힌 필드 $F$ 와 기본 등치인 것을 말합니다. 게다가, 임의의 고정된 명제 $φ$ 는 $C$ 에서 유지되는 것과 그것이 충분하게 큰 특성의 임의의 대수적으로 닫힌 필드에서 유지되는 것은 필요충분 조건입니다.^[48]

만약 $U$ 가 집합 $I$ 위의 극단-필터(ultrafilter)이고, $F i$ 가 $I$ 안의 모든 각 $i$ 에 대해 필드이면, $U$ 에 관한 $F i$ 의 극단-곱(ultraproduct)은 필드입니다.^[49] 그것은 다음에 의해 표시됩니다:

ulim i \to\infty F i

,

왜냐하면 그것은 필드 $F i$ 의 극한으로 여러 방법으로 행동하기 때문입니다: 워시의 정리(Łoś's theorem)는, 모두이지만 유한하게 많은 $φ$ 에 대해 유지되는 임의의 일차 명제는 초곱에 대해 역시 유지된다고 말합니다. 위의 문장 $φ$ 에 적용되면, 이것은 다음 동형-사상이 있음을 보입니다:^{[nb 5]}

\operatorname {ulim} _{p\to \infty }{\overline {\mathbf {F} }}_{p}\cong \mathbf {C} .

위에서 언급된 액스–코흔 정리는 이것 및 초곱의 동형-사상으로부터 따릅니다 (모든 소수 p에 걸쳐 둘 다 경우에서)

ulim p Q p ≅ ulim p F p ((t))

.

게다가, 모델 이론은, 실수 닫힌 필드(real closed field) 또는 (지수 함수 $exp : F \to F x$ 를 갖춘) 지수 필드(exponential field)와 같은, 필드의 다양한 다른 유형의 논리적 속성을 역시 연구합니다.^[50]

The absolute Galois group

대수적으로 닫혀 있지 않은 (또는 분해-가능한 닫혀 있지 않은) 필드에 대해, 절대 갈루아 그룹(absolute Galois group) $Gal(F)$ 은 근본적으로 중요합니다: 위에서 윤곽이 잡힌 유한 갈루아 확장의 경우를 확장하면, 이 그룹은 $F$ 의 모든 유한 분해-가능한 확장을 제어합니다. 초급 수단에 의해, 그룹 $Gal(F q)$ 은 프뤼퍼 그룹(Prüfer group), $Z$ 의 사유한 완비(profinite completion)인 것으로 보일 수 있습니다. 이 명제는 $Gal(F q)$ 의 오직 대수적 확장이 $n > 0$ 에 대해 필드 $Gal(F q n)$ 이고, 이들 유한 확장의 갈루아 그룹은 다음에 의해 주어진다는 사실을 포함합니다:

Gal(F q n / F q) = Z / n Z

.

생성기와 관계의 관점에서 설명은 $p$ -진수 숫자 필드 ( $Q p$ 의 유한 확장)의 갈루아 그룹에 대해 역시 알려져 있습니다.^[51]

갈루아 그룹의 표시(representations of Galois groups) 및 베유 그룹(Weil group)과 같은 관련 그룹의 표시는, 랭글랜즈 프로그램(Langlands program)과 같은 산술의 많은 가지에서 기본입니다. 그러한 표시의 코호몰로지 연구는 갈루아 코호몰로지(Galois cohomology)를 사용하여 행해집니다.^[52] 예를 들어, 중심 단순 $F$ -대수의 그룹으로 고전적으로 정의되는, 브라우어 그룹(Brauer 그룹)은 갈루아 코호몰로지(Galois cohomology) 그룹, 즉, 다음으로 재해석될 수 있습니다:

Br(F) = H 2 (F, G m)

.

K-theory

밀너 K-이론(Milnor K-theory)은 다음으로 정의됩니다:

K_{n}^{M}(F)=F^{\times }\otimes \cdots \otimes F^{\times }/\langle x\otimes (1-x)\mid x\in F\smallsetminus \{0,1\}\rangle .

블라디미르 보예보츠키(Vladimir Voevodsky)에 의해 2000년경에 입증된, 노름 잔여 동형-사상 정리(norm residue isomorphism theorem)는 다음 동형-사상을 수단으로 갈루아 코호몰로지에 이것을 관련 짓습니다:

K_{n}^{M}(F)/p=H^{n}(F,\mu _{l}^{\otimes n}).

대수적 K-이론(algebraic K-theory)은 주어진 필드의 계수를 갖는 역-가능한 행렬(invertible matrix)의 그룹과 관련됩니다. 예를 들어, 역-가능한 행렬의 행렬식(determinant)을 취하는 과정은 동형 K₁(F) = F^×로 이어집니다. 마츠모토의 정리(Matsumoto's theorem)는 K₂(F)는 K₂^M(F)와 일치한다는 것을 보입니다. 더-높은 차수에서, K-이론은 밀너 K-이론에서 분기하고 일반적으로 계산하기 어려운 것으로 남습니다.

Applications

Linear algebra and commutative algebra

Euler angles express the relation of different coordinate systems, i.e., bases of $R 3$ . They are used in computer graphics.

만약 $a \neq 0$ 이면, 방정식(equation)

ax = b

은 $F$ 안의 유일한 해 $x$ , 즉 $x = b / a$ 을 가집니다. 필드의 정의의 즉각적인 결과인, 이 관찰은, 임의의 벡터 공간(vector space)은 기저(basis)를 가지는 것을 보여주기 위해 사용된 필수적인 성분입니다.^[53] 대략 말하자면, 이것은 이론적인 관점, 및 역시 실용적인 응용에 대해 양쪽의 선형 대수(linear algebra)에서 핵심적 중요성인, 임의의 벡터 공간에서 좌표 시스템을 선택하는 것을 허용합니다.

정수의 링 Z를 포함하는, 대부분의 링(ring)에 걸쳐 (벡터 공간의 아날로그) 모듈(modules)은 보다 복잡한 구조를 가집니다. 특정 상황은, 링 $R$ 은 그 자체로 필드 $F$ 에 걸쳐 벡터 공간일 때, 발생합니다. 그러한 링은 $F$ -대수( $F$ -algebras)로 불리고 교환 대수(commutative algebra)의 영역에서 깊게 연구됩니다. 예를 들어, 뇌터 정규화(Noether normalization)는 임의의 유한하게 생성된 $F$ -대수가 다항식 링 $F [x 1, ..., x n]$ (보다 정확하게, 다항식 링에 걸쳐 모듈로 유한하게 생성된)와 밀접하게 관련된 것을 단언합니다.^[54]

Finite fields: cryptography and coding theory

The sum of three points P, Q, and R on an elliptic curve E (red) is zero if there is a line (blue) passing through these points.

광범위하게 적용되는 암호화 루틴은 이산 지수, 즉, (큰) 유한 필드 $F q$ 에서 계산

a n = a \cdot a \cdot ... \cdot a

(

n

factors, for an integer

n \geq 1

)

은, 역 연산, 즉, 방정식

a n = b

의 해 $n$ 을 결정하는, 이산 로그(discrete logarithm)보다 훨씬 더 효율적으로 수행될 수 있다는 사실을 사용합니다.

타원 곡선 암호화(elliptic curve cryptography)에서, 유한 필드에서 곱셈은 타원 곡선(elliptic curve) 위의 점을 더하는 연산, 즉, 형식

y 2 = x 3 + ax + b

의 방정식의 해에 의해 대체됩니다.

유한 필드는 코드 이론(coding theory) 및 조합론(combinatorics)에서 역시 사용됩니다.

Geometry: field of functions

필드 $k$ 로의 적절한 토폴로지적 공간(topological space) $X$ 위의 함수(Functions)는 점별로 더해지고 곱해질 수 있습니다. 예를 들어, 두 함수의 곱은 도메인 안의 그들 값의 곱에 의해 정의됩니다:

(f \cdot g)(x) = f (x) \cdot g (x)

.

이것은 이들 함수 $k$ -교환 대수(commutative algebra)를 만듭니다.

함수의 필드를 가지는 것에 대해, 우리는 정수 도메인(integral domains)인 함수의 대수를 반드시 고려해야 합니다. 이 경우에서 두 함수의 비율, 즉, 형식

{\frac {f(x)}{g(x)}}

의 표현은 필드를 형성하며, 함수의 필드로 불립니다.

이것은 두 주요 경우에서 발생합니다. $X$ 가 복소수 매니폴드(complex manifold) $X$ 일 때, 이 경우에서, 우리는 정칙 함수(holomorphic functions), 즉, 복소수 미분-가능한 함수의 대수를 고려합니다. 그들의 비율은 $X$ 위의 유리형 함수(meromorphic function)의 필드를 형성합니다.

(다항 방정식의 공통 영으로 정의된 기하학적 대상) 대수적 다양체(algebraic variety) $X$ 의 함수 필드(function field)는 정규 함수(regular function)의 비율, 즉, 다양체 위의 다항 함수의 비율로 구성됩니다. 필드 $k$ 에 걸쳐 $n$ -차원 공간(space)의 함수 필드는 $k (x 1, ..., x n)$ , 즉, $n$ 불확정에서 다항식의 비율로 구성되는 필드입니다. $X$ 의 함수 필드는 임의의 열린(open) 밀집한 부분-다양체 중 하나와 같습니다. 다른 말로, 함수 필드는 (약간) 더-작은 부분-다양체에 의해 $X$ 를 대체하는 것에 둔감합니다.

함수 필드는 동형-사상(isomorphism)과 다양체의 쌍유리 동치(birational equivalence) 아래에서 불변입니다. 그것은 추상 대수적 다양체(abstract algebraic variety)의 연구 및 대수적 다양체의 분류에 대해 그러므로 중요한 도구입니다. 예를 들어, $k (X)$ 의 초월 차수와 같은 차원(dimension)은 쌍유리 동치 아래에서 불변입니다.^[55] 곡선(curves) (즉, 차원이 일인 것)에 대해, 함수 필드 $k (X)$ 는 $X$ 에 매우 가깝습니다: 만약 $X$ 가 매끄러운(smooth) 및 적절한(proper) (컴팩트(compact)인 것의 아날로그) 것이면, $X$ 는, 함수의 그의 필드로부터, 동형-사상까지(up to), 재구성될 수 있습니다.^{[nb 6]} 더-높은 차원에서, 함수 필드는 $X$ 에 대한 덜이지만, 여전히 결정적인 정보를 기억합니다. 더 높은 차원에서 함수 필드 및 그들 기하학적 의미의 연구는 쌍유리 기하학(birational geometry)을 참조됩니다. 최소 모델 프로그램(minimal model program)은 규정된 함수 필드를 갖는 가장-간단한 (어떤 정확한 의미에서) 대수적 다양체를 식별하려고 시도합니다.

Number theory: global fields

전역 필드(global field)는 대수적 숫자 이론(algebraic number theory) 및 산술 기하학(arithmetic geometry)에서 각광 받습니다. 그들은, 정의에 의해, 숫자 필드(number field) ( $Q$ 의 유한 확장) 또는 $F q$ ( $F q (t)$ 의 유한 확장)에 걸쳐 함수 필드입니다. 지역 필드에 대한 것처럼, 필드의 이들 두 유형은 비록 그들이, 각각, 특성 0 및 양의 특성일지라도, 여러 비슷한 특색을 공유합니다. 이 함수 필드 아날로그(function field analogy)는, 종종 먼저 함수 필드에 대한 질문을 이해함으로써, 및 나중에 숫자 필드 경우를 처리함으로써, 수학적 기대를 구체화하는 것에 도움이 될 수 있습니다. 후자는 종종 보다 어렵습니다. 예를 들어, (2017년에 열린) 리만 제타 함수(Riemann zeta function)의 영에 관련한 리만 가설(Riemann hypothesis)은 베유 추측(Weil conjectures)과 평행인 것으로 여길 수 있습니다 (피에르 들리뉴(Pierre Deligne)에 의해 1974년에 입증되었습니다).

The fifth roots of unity form a regular pentagon.

사이클로토먹 필드(cyclotomic field:원형의 필드)는 가장 격렬히 연구된 숫자 필드 중 하나입니다. 그것들은 형식 $Q (ζ n)$ 의 것이며, 여기서 $ζ n$ 은 단위의 원시 $n$ -번째 근, 즉, 모든 $m < n$ 에 대해, $ζ n = 1$ 및 $ζ m \neq 1$ 을 만족시키는 복소수입니다.^[56] 정규 소수(regular prime)인 $n$ 에 대해, 쿠머(Kummer)는 페르마의 마지막 정리(Fermat's last theorem)를 입증하기 위해 원형의 필드를 사용했으며, 이것은 방정식

x n + y n = z n

에 대한 유리수 비-영 해의 비-존재성을 주장합니다.

지역 필드는 전역 필드의 완비입니다. 오스트롭스키의 정리(Ostrowski's theorem)는, $Q$ 의 오직 완비, 하나의 전역 필드는 지역 필드 $Q p$ 및 $R$ 임을 주장합니다. 전역 필드에서 산술 질문을 연구하면 때때로 지역적으로 해당하는 질문을 살펴봄으로써 행해질 수 있을 것입니다. 이 기법은 지역-전역 원리(local-global principle)로 불립니다. 예를 들어, 하세–민코프스키 정리(Hasse–Minkowski theorem)는 이차 방정식의 유리수 해를 찾는 문제를, 그의 해가 쉽게 묘사될 수 있는, $R$ 및 $Q p$ 에서 이들 방정식을 푸는 것으로 줄입니다.^[57]

지역 필드와 달리, 전역 필드의 갈루아 그룹은 알려져 있지 않습니다. 역 갈루아 이론(inverse Galois theory)은, 임의의 유한 그룹이 어떤 숫자 필드 $F$ 에 대해 갈루아 그룹 $Gal(F / Q)$ 인지 여부 (미해결) 문제를 연구합니다.^[58] 클래스 필드 이론(class field theory)은 아벨 확장(abelian extension), 즉, 아벨 갈루아 그룹을 갖는 것, 또는 동등하게 전역 필드의 아벨화된 갈루아 그룹을 설명합니다. 고전적인 명제, 크로네커–베버 정리(Kronecker–Weber theorem)는 $Q$ 의 극대 아벨 $Q ab$ 확장을 설명합니다: 그것은 단위의 모든 원시 $n$ -번째 근에 인접함으로써 얻어진 다음 필드입니다:

Q (ζ n, n \geq 2)

.

크로네커의 유겐트트라움(Kronecker's Jugendtraum:크로네터의 청춘의 꿈)은 일반적인 숫자 필드 $F$ 의 $F ab$ 의 비슷하게 명시적 설명에 대해 묻습니다. 허수 이차 필드(imaginary quadratic field), $F=\mathbf {Q} ({\sqrt {-d}})$ , $d > 0$ 에 대해, 복소수 곱셈(complex multiplication)의 이론은 타원 곡선(elliptic curves)을 사용하여 $F ab$ 를 설명합니다. 일반 숫자 필드에 대해, 그러한 명시적 설명이 알려져 있지 않습니다.

Related notions

필드가 즐길 수 있는 덧셈의 구조 외에도, 필드는 다양한 다른 관련 개념을 인정합니다. 임의의 필드에서 0 ≠ 1이므로, 임의의 필드는 적어도 두 원소를 가집니다. 그럼에도 불구하고, $p$ 가 1로 가는 경향이 있을 때, 유한 필드 $F p$ 의 극한이 되는 것으로 제안되는, 하나의 원소를 갖는 필드(field with one element)의 개념이 있습니다.^[59] 나눗셈 링 외에도, 준-필드(quasifield), 근거리-필드(near-field) 및 반-필드(semifield)와 같은 필드와 관련된 다양한 다른 더-약한 대수적 구조가 있습니다.

대문자 F를 갖는, Fields라고 때때로 불리는, 필드 구조를 갖는 역시 적절한 클래스(proper class)가 있습니다. 초현실수(surreal number)는 실수를 포함하는 Field를 형성하고, 그들이 집합이 아닌 적절한 클래스라는 사실을 제외하는 필드일 것습니다. 게임 이론(game theory)으로부터 개념, 님버(nimber)는 마찬가지로 그러한 Field를 형성합니다.^[60]

Division rings

필드의 정의 안에 하나 또는 여러 공리를 떨어뜨리면 다른 대수적 구조로 이어집니다. 위에서 언급한 것처럼, 교환 링은, 곱셈의 역을 제외하고, 필드의 모든 필드를 만족시킵니다. 곱셈이 교환-가능이라는 조건을 대신에 떨어뜨리면 나눗셈 링(division ring) 또는 스큐 필드(skew field)의 개념으로 이어집니다.^{[nb 7]} 유한 차원 $R$ -벡터 공간인 오직 나눗셈 링은 $R$ 자체, (필드인) $C$ , (곱셈이 비-교환인) 쿼터니언(quaternion) $H$ , 및 (곱셈이 비-교환이고 비-결합인) 옥토니언(octonion) $O$ 입니다. 이 사실은 미셸 케르베르(Michel Kervaire), 라울 보트(Raoul Bott), 및 존 밀너(John Milnor)에 의해 1958년에 대수적 토폴로지(algebraic topology)의 방법을 사용하여 입증되었습니다.^[61] 홀수-차원 나눗셈 대수의 비-존재성이 보다 고전적입니다. 그것은 오른쪽에서 그려진 털난 공 정리(hairy ball theorem)로부터 추론될 수 있습니다.

Notes

^ The a priori twofold use of the symbol "−" for denoting one part of a constant and for the additive inverses is justified by this latter condition.
^ Equivalently, a field is an algebraic structure $⟨ F, +, \cdot, -, -1, 0, 1⟩$ of type $⟨2, 2, 1, 1, 0, 0⟩$ , such that $0 -1$ is not defined, $⟨ F, +, -, 0⟩$ and $⟨ F ∖ {0}, \cdot, -1 ⟩$ are abelian groups, and · is distributive over +. Wallace (1998, Th. 2)
^ Further examples include the maximal unramified extension or the maximal abelian extension within $F$ .
^ Some authors also consider the fields $R$ and $C$ to be local fields. On the other hand, these two fields, also called Archimedean local fields, share little similarity with the local fields considered here, to a point that Cassels (1986, p. vi) calls them "completely anomalous".
^ Both $C$ and $ulim p F p$ are algebraically closed by Łoś's theorem. For the same reason, they both have characteristic zero. Finally, they are both uncountable, so that they are isomorphic.
^ More precisely, there is an equivalence of categories between smooth proper algebraic curves over an algebraically closed field $F$ and finite field extensions of $F (T)$ .
^ Historically, division rings were sometimes referred to as fields, while fields were called commutative fields.

^ Beachy & Blair (2006, Definition 4.1.1, p. 181)
^ Clark (1984, Chapter 3)
^ Mines, Richman & Ruitenburg (1988, §II.2). See also Heyting field.
^ Beachy & Blair (2006, p. 120, Ch. 3)
^ Artin (1991, Chapter 13.4)
^ Lidl & Niederreiter (2008, Example 1.62)
^ Beachy & Blair (2006, p. 120, Ch. 3)
^ Sharpe (1987, Theorem 1.3.2)
^ Adamson (2007, §I.2, p. 10)
^ Escofier (2012, 14.4.2)
^ Adamson (2007, section I.3)
^ Adamson (2007, p. 12)
^ Lidl & Niederreiter (2008, Lemma 2.1, Theorem 2.2)
^ Lidl & Niederreiter (2008, Theorem 1.2.5)
^ Kleiner (2007, p. 63)
^ Kiernan (1971, p. 50)
^ Bourbaki (1994, pp. 75–76)
^ Corry (2004, p.24)
^ Earliest Known Uses of Some of the Words of Mathematics (F)
^ Dirichlet (1871, p. 42), translation by Kleiner (2007, p. 66)
^ Bourbaki (1994, p. 81)
^ Corry (2004, p. 33). See also Fricke & Weber (1924).
^ Bourbaki (1994, p. 92)
^ Lang (2002, §II.1)
^ Artin (1991, Section 10.6)
^ Eisenbud (1995, p. 60)
^ Jacobson (2009, p. 213)
^ Artin (1991, Theorem 13.3.4)
^ Artin (1991, Corollary 13.3.6)
^ Bourbaki (1988, Chapter V, §14, No. 2, Theorem 1)
^ Artin (1991, Section 13.9)
^ Banaschewski (1992). Mathoverflow post
^ Ribenboim (1999, p. 186, §7.1)
^ Bourbaki (1988, Chapter VI, §2.3, Corollary 1)
^ Lorenz (2008, §22, Theorem 1)
^ Prestel (1984, Proposition 1.22)
^ Prestel (1984, Theorem 1.23)
^ Warner (1989, Chapter 14)
^ Gouvêa (1997, §5.7)
^ Serre (1979)
^ Scholze (2014)
^ van der Put & Singer (2003, §1)
^ Lang (2002, Theorem V.4.6)
^ Lang (2002, §VI.1)
^ Lang (2002, Example VI.2.6)
^ Borceux & Janelidze (2001). See also Étale fundamental group.
^ Gouvêa (2012, Theorem 6.4.8)
^ Marker, Messmer & Pillay (2006, Corollary 1.2)
^ Schoutens (2002, §2)
^ Kuhlmann (2000)
^ Jannsen & Wingberg (1982)
^ Serre (2002)
^ Artin (1991, §3.3)
^ Eisenbud (1995, Theorem 13.3)
^ Eisenbud (1995, §13, Theorem A)
^ Washington (1997)
^ Serre (1978, Chapter IV)
^ Serre (1992)
^ Tits (1957)
^ Conway (1976)
^ Baez (2002)

References

Adamson, I. T. (2007), Introduction to Field Theory, Dover Publications, ISBN 978-0-486-46266-0
Allenby, R. B. J. T. (1991), Rings, Fields and Groups, Butterworth-Heinemann, ISBN 978-0-340-54440-2
Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-13-004763-2, especially Chapter 13
Artin, Emil; Schreier, Otto (1927), "Eine Kennzeichnung der reell abgeschlossenen Körper", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg (in German), 5: 225–231, doi:10.1007/BF02952522, ISSN 0025-5858, JFM 53.0144.01
Ax, James (1968), "The elementary theory of finite fields", Ann. of Math., 2, 88: 239–271, doi:10.2307/1970573
Baez, John C. (2002), "The octonions", Bulletin of the American Mathematical Society, 39: 145–205, doi:10.1090/S0273-0979-01-00934-X
Banaschewski, Bernhard (1992), "Algebraic closure without choice.", Z. Math. Logik Grundlagen Math., 38 (4): 383–385, Zbl 0739.03027
Beachy, John. A; Blair, William D. (2006), Abstract Algebra (3 ed.), Waveland Press, ISBN 1-57766-443-4
Blyth, T. S.; Robertson, E. F. (1985), Groups, rings and fields: Algebra through practice, Cambridge University Press. See especially Book 3 (ISBN 0-521-27288-2) and Book 6 (ISBN 0-521-27291-2).
Borceux, Francis; Janelidze, George (2001), Galois theories, Cambridge University Press, ISBN 0-521-80309-8, Zbl 0978.12004
Bourbaki, Nicolas (1994), Elements of the history of mathematics, Springer, doi:10.1007/978-3-642-61693-8, ISBN 3-540-19376-6, MR 1290116
Bourbaki, Nicolas (1988), Algebra II. Chapters 4–7, Springer, ISBN 0-387-19375-8
Cassels, J. W. S. (1986), Local fields, London Mathematical Society Student Texts, vol. 3, Cambridge University Press, doi:10.1017/CBO9781139171885, ISBN 0-521-30484-9, MR 0861410
Clark, A. (1984), Elements of Abstract Algebra, Dover Books on Mathematics Series, Dover Publications, ISBN 978-0-486-64725-8
Conway, John Horton (1976), On Numbers and Games, Academic Press Inc. (London) Ltd.
Corry, Leo (2004), Modern algebra and the rise of mathematical structures (2nd ed.), Birkhäuser, ISBN 3-7643-7002-5, Zbl 1044.01008
Dirichlet, Peter Gustav Lejeune (1871), Dedekind, Richard (ed.), Vorlesungen über Zahlentheorie (Lectures on Number Theory) (in German), vol. 1 (2nd ed.), Braunschweig, Germany: Friedrich Vieweg und Sohn
Eisenbud, David (1995), Commutative algebra with a view toward algebraic geometry, Graduate Texts in Mathematics, vol. 150, New York: Springer-Verlag, ISBN 0-387-94268-8, MR 1322960
Escofier, J. P. (2012), Galois Theory, Springer, ISBN 978-1-4613-0191-2
Fricke, Robert; Weber, Heinrich Martin (1924), Lehrbuch der Algebra (in German), Vieweg, JFM 50.0042.03
Gouvêa, Fernando Q. (1997), p-adic numbers, Universitext (2nd ed.), Springer
Gouvêa, Fernando Q. (2012), A Guide to Groups, Rings, and Fields, Mathematical Association of America, ISBN 978-0-88385-355-9
"Field", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Hensel, Kurt (1904), "Über eine neue Begründung der Theorie der algebraischen Zahlen", Journal für die Reine und Angewandte Mathematik (in German), 128: 1–32, ISSN 0075-4102, JFM 35.0227.01
Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
Jannsen, Uwe; Wingberg, Kay (1982), "Die Struktur der absoluten Galoisgruppe 𝔭-adischer Zahlkörper. [The structure of the absolute Galois group of 𝔭-adic number fields]", Invent. Math., 70 (1): 71–98, doi:10.1007/bf01393199, MR 0679774
Kleiner, Israel (2007), A history of abstract algebra, Birkhäuser, doi:10.1007/978-0-8176-4685-1, ISBN 978-0-8176-4684-4, MR 2347309
Kiernan, B. Melvin (1971), "The development of Galois theory from Lagrange to Artin", Archive for History of Exact Sciences, 8 (1–2): 40–154, doi:10.1007/BF00327219, MR 1554154
Kuhlmann, Salma (2000), Ordered exponential fields, Fields Institute Monographs, vol. 12, American Mathematical Society, ISBN 0-8218-0943-1, MR 1760173
Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (3rd ed.), Springer, doi:10.1007/978-1-4613-0041-0, ISBN 0-387-95385-X
Lidl, Rudolf; Niederreiter, Harald (2008), Finite fields (2nd ed.), Cambridge University Press, ISBN 978-0-521-06567-2, Zbl 1139.11053
Lorenz, Falko (2008), Algebra, Volume II: Fields with Structures, Algebras and Advanced Topics, Springer, ISBN 978-0-387-72487-4
Marker, David; Messmer, Margit; Pillay, Anand (2006), Model theory of fields, Lecture Notes in Logic, vol. 5 (2nd ed.), Association for Symbolic Logic, CiteSeerX 10.1.1.36.8448, ISBN 978-1-56881-282-3, MR 2215060
Mines, Ray; Richman, Fred; Ruitenburg, Wim (1988), A course in constructive algebra, Universitext, Springer, ISBN 0-387-96640-4, MR 0919949
Moore, E. Hastings (1893), "A doubly-infinite system of simple groups", Bulletin of the American Mathematical Society, 3 (3): 73–78, doi:10.1090/S0002-9904-1893-00178-X, MR 1557275
Prestel, Alexander (1984), Lectures on formally real fields, Lecture Notes in Mathematics, vol. 1093, Springer, doi:10.1007/BFb0101548, ISBN 3-540-13885-4, MR 0769847{{citation}}: CS1 maint: extra punctuation (link)
Ribenboim, Paulo (1999), The theory of classical valuations, Springer Monographs in Mathematics, Springer, doi:10.1007/978-1-4612-0551-7, ISBN 0-387-98525-5, MR 1677964
Scholze, Peter (2014), "Perfectoid spaces and their Applications" (PDF), Proceedings of the International Congress of Mathematicians 2014, ISBN 978-89-6105-804-9
Schoutens, Hans (2002), The Use of Ultraproducts in Commutative Algebra, Lecture Notes in Mathematics, vol. 1999, Springer, ISBN 978-3-642-13367-1
Serre, Jean-Pierre (1978), A course in arithmetic. Translation of Cours d'arithmetique, Graduate Text in Mathematics, vol. 7 (2nd ed.), Springer, Zbl 0432.10001
Serre, Jean-Pierre (1979), Local fields, Graduate Texts in Mathematics, vol. 67, Springer, ISBN 0-387-90424-7, MR 0554237
Serre, Jean-Pierre (1992), Topics in Galois theory, Jones and Bartlett Publishers, ISBN 0-86720-210-6, Zbl 0746.12001
Serre, Jean-Pierre (2002), Galois cohomology, Springer Monographs in Mathematics, Translated from the French by Patrick Ion, Berlin, New York: Springer-Verlag, ISBN 978-3-540-42192-4, MR 1867431, Zbl 1004.12003
Sharpe, David (1987), Rings and factorization, Cambridge University Press, ISBN 0-521-33718-6, Zbl 0674.13008
Steinitz, Ernst (1910), "Algebraische Theorie der Körper" [Algebraic Theory of Fields], Journal für die reine und angewandte Mathematik, 137: 167–309, doi:10.1515/crll.1910.137.167, ISSN 0075-4102, JFM 41.0445.03
Tits, Jacques (1957), "Sur les analogues algébriques des groupes semi-simples complexes", Colloque d'algèbre supérieure, tenu à Bruxelles du 19 au 22 décembre 1956, Centre Belge de Recherches Mathématiques Établissements Ceuterick, Louvain, Paris: Librairie Gauthier-Villars, pp. 261–289
van der Put, M.; Singer, M. F. (2003), Galois Theory of Linear Differential Equations, Grundlehren der mathematischen Wissenschaften, vol. 328, Springer
von Staudt, Karl Georg Christian (1857), Beiträge zur Geometrie der Lage (Contributions to the Geometry of Position), vol. 2, Nürnberg (Germany): Bauer and Raspe
Wallace, D. A. R. (1998), Groups, Rings, and Fields, SUMS, vol. 151, Springer
Warner, Seth (1989), Topological fields, North-Holland, ISBN 0-444-87429-1, Zbl 0683.12014
Washington, Lawrence C. (1997), Introduction to Cyclotomic Fields, Graduate Texts in Mathematics, vol. 83 (2 ed.), New York: Springer-Verlag, ISBN 0-387-94762-0, MR 1421575
Weber, Heinrich (1893), "Die allgemeinen Grundlagen der Galois'schen Gleichungstheorie", Mathematische Annalen (in German), 43: 521–549, doi:10.1007/BF01446451, ISSN 0025-5831, JFM 25.0137.01

[4] The a priori twofold use of the symbol "−" for denoting one part of a constant and for the additive inverses is justified by this latter condition.

[9] Equivalently, a field is an algebraic structure $⟨ F, +, \cdot, -, -1, 0, 1⟩$ of type $⟨2, 2, 1, 1, 0, 0⟩$ , such that $0 -1$ is not defined, $⟨ F, +, -, 0⟩$ and $⟨ F ∖ {0}, \cdot, -1 ⟩$ are abelian groups, and · is distributive over +. Wallace (1998, Th. 2)

[30] Further examples include the maximal unramified extension or the maximal abelian extension within $F$ .

[44] Some authors also consider the fields $R$ and $C$ to be local fields. On the other hand, these two fields, also called Archimedean local fields, share little similarity with the local fields considered here, to a point that Cassels (1986, p. vi) calls them "completely anomalous".

[54] Both $C$ and $ulim p F p$ are algebraically closed by Łoś's theorem. For the same reason, they both have characteristic zero. Finally, they are both uncountable, so that they are isomorphic.

[61] More precisely, there is an equivalence of categories between smooth proper algebraic curves over an algebraically closed field $F$ and finite field extensions of $F (T)$ .

[67] Historically, division rings were sometimes referred to as fields, while fields were called commutative fields.

[1] Beachy & Blair (2006, Definition 4.1.1, p. 181)

[2] Clark (1984, Chapter 3)

[3] Mines, Richman & Ruitenburg (1988, §II.2). See also Heyting field.

[5] Beachy & Blair (2006, p. 120, Ch. 3)

[6] Artin (1991, Chapter 13.4)

[7] Lidl & Niederreiter (2008, Example 1.62)

[8] Beachy & Blair (2006, p. 120, Ch. 3)

[10] Sharpe (1987, Theorem 1.3.2)

[11] Adamson (2007, §I.2, p. 10)

[12] Escofier (2012, 14.4.2)

[13] Adamson (2007, section I.3)

[14] Adamson (2007, p. 12)

[15] Lidl & Niederreiter (2008, Lemma 2.1, Theorem 2.2)

[16] Lidl & Niederreiter (2008, Theorem 1.2.5)

[17] Kleiner (2007, p. 63)

[18] Kiernan (1971, p. 50)

[19] Bourbaki (1994, pp. 75–76)

[20] Corry (2004, p.24)

[21] Earliest Known Uses of Some of the Words of Mathematics (F)

[22] Dirichlet (1871, p. 42), translation by Kleiner (2007, p. 66)

[23] Bourbaki (1994, p. 81)

[24] Corry (2004, p. 33). See also Fricke & Weber (1924).

[25] Bourbaki (1994, p. 92)

[26] Lang (2002, §II.1)

[27] Artin (1991, Section 10.6)

[28] Eisenbud (1995, p. 60)

[29] Jacobson (2009, p. 213)

[31] Artin (1991, Theorem 13.3.4)

[32] Artin (1991, Corollary 13.3.6)

[33] Bourbaki (1988, Chapter V, §14, No. 2, Theorem 1)

[34] Artin (1991, Section 13.9)

[35] Banaschewski (1992). Mathoverflow post

[36] Ribenboim (1999, p. 186, §7.1)

[37] Bourbaki (1988, Chapter VI, §2.3, Corollary 1)

[38] Lorenz (2008, §22, Theorem 1)

[39] Prestel (1984, Proposition 1.22)

[40] Prestel (1984, Theorem 1.23)

[41] Warner (1989, Chapter 14)

[42] Gouvêa (1997, §5.7)

[43] Serre (1979)

[45] Scholze (2014)

[46] van der Put & Singer (2003, §1)

[47] Lang (2002, Theorem V.4.6)

[48] Lang (2002, §VI.1)

[49] Lang (2002, Example VI.2.6)

[50] Borceux & Janelidze (2001). See also Étale fundamental group.

[51] Gouvêa (2012, Theorem 6.4.8)

[52] Marker, Messmer & Pillay (2006, Corollary 1.2)

[53] Schoutens (2002, §2)

[55] Kuhlmann (2000)

[56] Jannsen & Wingberg (1982)

[57] Serre (2002)

[58] Artin (1991, §3.3)

[59] Eisenbud (1995, Theorem 13.3)

[60] Eisenbud (1995, §13, Theorem A)

[62] Washington (1997)

[63] Serre (1978, Chapter IV)

[64] Serre (1992)

[65] Tits (1957)

[66] Conway (1976)

[68] Baez (2002)

[1]

[2]

[3]

[nb 1]

[4]

[5]

[6]

[7]

[nb 2]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[nb 3]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[nb 4]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[nb 5]

[50]

[51]

[52]

[53]

[54]

[55]

[nb 6]

[56]

[57]

[58]

[59]

[60]

[nb 7]

[61]