Cubic function

수학(mathematics)에서, 삼차 함수는 다음 형식의 함수(function)입니다:
여기서 계수 a, b, c, 및 d는 실수이고, 변수 x는 실수 값을 취하고, a ≠ 0입니다. 달리 말해서, 그것은 차수 삼의 다항 함수(polynomial function)이고, 실수 함수(real function)입니다. 특히, 도메인(domain)과 코도메인(codomain)은 실수의 집합입니다.
f(x) = 0를 설정하면 다음 형식의 삼차 방정식(cubic equation)을 산출합니다:
그의 해는 함수의 근(roots)으로 불립니다.
삼차 함수는 하나 또는 셋의 실수 근을 가집니다 (적어도 하나의 실수 근의 존재는 모든 홀수-차수 다항식 함수에 대해 참입니다).
삼차 함수의 그래프(graph)는 단일 변곡점(inflection point)을 가집니다. 그것은 두 개의 임계점(critical points), 지역 최솟값과 지역 최댓값을 가질 수 있습니다. 그렇지 않으면, 삼차 함수는 단조적(monotonic)입니다. 삼차 함수의 그래프는 그것의 변곡점에 관해 대칭입니다; 즉, 그것은 이 지점을 중심으로 반 바퀴 회전 아래에서 불변입니다. 아핀 변환(affine transformation)까지(up to), 삼차 함수에 대해 오직 세 개의 가능한 그래프가 있습니다.
삼차 함수는 삼차 보간(cubic interpolation)에 대해 기본입니다.
History
Critical and inflection points

삼차 함수의 임계 점(critical points)은 그것의 정류 점(stationary point), 즉 함수의 기울기가 영인 점입니다. 따라서 삼차 함수 f의 임계 점은 삼차 함수의 도함수(derivative)가 영인 것을 만족하는
x의 값에서 발생하는 다음에 의해 정의됩니다:
- f(x) = ax3 + bx2 + cx + d.
이 방정식의 해는 임계 점의 x-값이고, 이차 공식(quadratic formula)을 사용하여, 다음에 의해 제공됩니다:
제곱근 내부의 표현의 부호는 임계 점의 숫자를 결정합니다. 만약 그것이 양수이면, 두 개의 임계점이 있으며, 하나는 지역 최댓값이고, 다른 하나는 지역 최솟값입니다. 만약 b2 – 3ac = 0이면, 오직 하나의 임계점이 있으며, 이것은 변곡점(inflection point)입니다. 만약 b2 – 3ac < 0이면, (실수) 임계점은 없습니다. 두 가지 후자의 경우에서, 즉, 만약 b2 – 3ac가 비-음이면, 삼차 함수는 엄격하게 단조적(monotonic)입니다. 경우 Δ0 > 0의 예제에 대해 그림을 참조하십시오.
함수의 임계점은 해당 함수가 오목성(concavity)을 변경하는 곳입니다. 변곡점은 이차 도함수(second derivative)가 영이고, 삼차 도함수가 비-영일 때 발생합니다. 따라서 삼차 함수는 항상 단일 변곡점이 있으며, 이것은 다음에서 발생합니다:
Classification
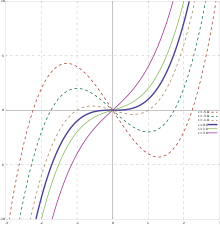
The graph of any cubic function is similar to such a curve.
삼차 함수의 그래프(graph)는 삼차 곡선(cubic curve)의 예제입니다. (많은 삼차 곡선은 함수의 그래프가 아닙니다.)
비록 삼차 함수가 네 개의 매개-변수에 의존하지만, 그들의 그래프가 단지 아주 적은 모양을 가집니다. 사실, 삼차 함수의 그래프는 항상 다음 형식의 함수의 그래프와 닮아(similar) 있습니다:
이 닮음은 좌표축에 평행한 평행이동(translation), 닮음-변환(homothecy) (균등 스케일링(uniform scaling)), 및, 아마도, y-축에 관한 반사(reflection) (거울 이미지(mirror image))의 합성으로 조립될 수 있습니다. 게다가 비-균등 스케일링(non-uniform scaling)은 그래프를 세 개의 삼차 함수 중 하나의 그래프로 변환할 수 있습니다:
이것은 아핀 변환(affine transformation)까지(up to) 삼차 함수의 오직 세 그래프가 있음을 의미합니다.
위의 기하 변환(geometric transformation)은, 일반적인 삼차 함수 에서 시작할 때, 다음 방법으로 조립될 수 있습니다.
먼저, 만약 a < 0이면, 변수의 변경(change of variable) x → –x은 a > 0을 가정하는 것을 허용합니다. 이 변수의 변화 후에, 새로운 그래프는 y-축에 관한 이전 것의 거울 이미지입니다.
그런-다음, 변수의 변경 x = x1 – b/3a은 다음 형식의 함수를 제공합니다:
이것은 x-축에 평행한 평행-이동에 해당합니다.
변수의 변경 y = y1 + q은 y-축에 관한 평행-이동에 해당하고, 다음 형식의 함수를 제공합니다:
변수의 변경 은 균등 스케일링에 해당하고, 으로 나눈 후에, 다음 형식의 함수를 제공합니다:
이것은 닮음에 의해 얻어질 수 있는 가장-간단한 형식입니다.
그런-다음, 만약 p ≠ 0이면, 비-균등 스케일링 은, 로 나눈 후에, 다음을 제공합니다:
여기서 는, p의 부호에 따라, 값 1 또는 –1을 가집니다. 만약 우리가 를 정의하면, 함수의 후자 형식은 모든 경우에 적용됩니다.
Symmetry
형식 의 삼차 함수에 대해, 변곡점이 따라서 원점입니다. 그러한 함수는 홀수 함수(odd function)이므로, 그것의 그래프는 변곡점에 관해 대칭이고, 변곡점을 중심으로 반 바퀴 회전 아래에서 불변입니다. 이들 속성은 닮음(similarity)에 의해 불변이므로, 모든 것은 모든 삼차 함수에 대해 참입니다.
삼차 함수의 그래프는 그것의 변곡점에 관해 대칭이고, 변곡점을 중심으로 반 바퀴 회전 아래에서 불변입니다.
Collinearities

세 개의 같은-직선-위의 점(collinear points)에서 삼차 함수의 그래프에 대한 접선은 같은-직선-위의 점에서 다시 삼차와 교차합니다.[1] 이것은 다음처럼 보일 수 있습니다.
이 속성은 강체 운동 아래에서 불변이므로, 우리는 함수가 다음 형식을 가지는 것으로 가정할 수 있습니다:
만약 α가 실수이면, 점 (α, f(α))에서 f의 그래프에 대한 접선은 다음 직선입니다:
- {(x, f(α) + (x − α)f ′(α)) : x ∈ R}.
따라서, 이 직선과 f의 그래프 사이의 교차 점은 방정식 f(x) = f(α) + (x − α)f ′(α)을 풀면, 즉, 다음을 풀어서 얻어질 수 있습니다:
이것은 다음으로 다시-쓸 수 있습니다:
그리고 다음으로 인수화될 수 있습니다:
따라서, 접선은 다음에서 삼차와 교차합니다:
따라서, 그래프의 점 (x, y)를 접선이 그래프를 교차하는 다른 점에 매핑하는 함수는 다음입니다:
이것은 같은-직선-위의 점을 같은-직선-위의 점으로 변환하는 아핀 변환(affine transformation)입니다. 이것은 주장된 결과를 입증합니다.
Cubic interpolation
두 점에서 함수와 그것의 도함수의 값이 주어지면, 같은 네 값을 가지는 정확히 하나의 삼차 함수가 있으며, 이것은 삼차 에르미트 스플라인(cubic Hermite spline)으로 불립니다.
이 사실을 사용하는 두 가지 표준 방법이 있습니다. 먼저, 만약 우리가, 예를 들어 물리적 측정, 함수의 값 및 일부 표본화 점에서 그것의 도함수의 값을 알면, 우리는 함수를 연속적으로 미분-가능 함수(continuously differentiable function)로 보간할 수 있으며, 이것은 조각별(piecewise) 삼차 함수입니다.
만약 함수의 값은 여러 점에서 알려져 있으면, 삼차 보간(cubic interpolation)은 연속적인 미분-가능 함수(continuously differentiable function)에 의해 함수를 근사화하는 것으로 구성되며, 이것은 조각별(piecewise) 삼차입니다. 고유하게 정의된 보간을 가지는 것에 대해, 끝점에서 도함수의 값, 또는 끝점에서 영 곡률(curvature)과 같은, 두 가지 더 구속-조건은 더해져야 합니다.
Reference
- ^ Whitworth, William Allen (1866), "Equations of the third degree", Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Cambridge: Deighton, Bell, and Co., p. 425, retrieved June 17, 2016
External links
- "Cardano formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- History of quadratic, cubic and quartic equations on MacTutor archive.

























