Limit of a sequence

n	n sin(1/n)
1	0.841471
2	0.958851
...
10	0.998334
...
100	0.999983

As the positive integer $n$ becomes larger and larger, the value $n\cdot \sin \left({\tfrac {1}{n}}\right)$ becomes arbitrarily close to $1$ . We say that "the limit of the sequence $n\cdot \sin \left({\tfrac {1}{n}}\right)$ equals $1$ ."

수학(mathematics)에서, 수열의 극한(limit of a sequence)은 수열(sequence)의 항이 "경향이 있는(tend to)" 값입니다.^[1] 만약 그러한 극한이 존재하면, 수열은 수렴한다라고 불립니다. 수렴하지 않는 수열은 발산한다라고 말합니다.^[2] 수열의 극한은 해석학(analysis)의 전체가 궁극적으로 걸려 있는 것 위에 기본적인 개념으로 말합니다.^[1]

극한은 임의의 메트릭(metric) 또는 토폴로지적 공간(topological space)에서 정의될 수 있지만, 실수(real number)에서 보통 처음으로 만납니다.

History

그리스 철학자 엘레아의 제논(Zeno of Elea)은 극한적인 프로세스를 포함하는 역설을 공식화하는 것으로 유명합니다.

루시퍼스(Leucippus), 데모크리토스(Democritus), 앤터펀(Antiphon), 에우독소스(Eudoxus) 및 아르키메데스(Archimedes)는 넓이 또는 부피를 결정하기 위해 근사의 무한 수열을 사용하는, 소진의 방법(method of exhaustion)을 개발했습니다. 아르키메데스는 지금 기하 급수(geometric series:등비급수)라고 불리는 것을 합하는 것에 성공했습니다.

뉴턴(Newton)은 그의 연구 (1669년에 쓰이고, 사본으로 회람되고, 1711년에 출판되는) Analysis with infinite series, (1671년에 쓰이고, 1736년에 영문 번역이 출판되는, 한참 후에 출판된 라틴어 원본) Method of fluxions and infinite series 및 (1693년에 쓰이고, 그의 Optiks에 부록으로 1704년에 출판되는) Tractatus de Quadratura Curvarum에서 급수를 다룹니다. 후자의 연구에서, 뉴턴은 (x + o)ⁿ의 이항 전개를 고려했으며 그는 그런-다음 (o → 0으로 놓고) 극한을 취함으로써 그것을 선형화합니다.

18세기에서, 오일러(Euler)와 같은 수학자들(mathematician)은 적절한 순간에 멈춤으로써 일부 발산하는 급수를 합하는 것에 성공했습니다; 그들은, 극한이 계산될 수 있는 것만큼 오래, 그것이 존재했는지 여부에는 많은 관심을 두지 않았습니다. 18세기 말에 라그랑주(Lagrange)는, 그의 책 Théorie des fonctions analytiques (1797)에서, 엄격함의 부족이 미적분학에서 그 이상의 발전을 배제한다고 주장했습니다. 가우스(Gauss)는 초기하 급수(hypergeometric series) (1813)의 그의 연구에서 처음으로 어떤 조건 아래에서 급수가 하나의 극한에 수렴하는지를 엄격하게 조사했습니다.

극한의 현대적인 정의 (임의의 ε에 대해 ...이 되도록 인덱스 N이 존재합니다)는 (Der binomische Lehrsatz, 프라하 1816년, 그 당시에는 거의 주목받지 못한) 베르나르 볼차노(Bernhard Bolzano)와 1870년대 카를 바이어슈트라스(Karl Weierstrass)에 의해 제공되었습니다.

Real numbers

실수(real numbers)에서, 숫자 $L$ 은, 만약 수열에서 숫자가 $L$ 에 점점 더 가까워지고 임의의 다른 숫자에는 그렇지 않으면, 수열(sequence) $(x_{n})$ 의 극한(limit)입니다.

Examples

만약 상수 c에 대해 $x_{n}=c$ 이면, $x_{n}\to c$ 입니다.^{[proof 1]}
만약 $x_{n}={\frac {1}{n}}$ 이면, $x_{n}\to 0$ 입니다.^{[proof 2]}
만약 $n$ 이 짝수일 때 $x_{n}=1/n$ 이고, $n$ 이 홀수일 때 $x_{n}={\frac {1}{n^{2}}}$ 이면, $x_{n}\to 0$ 입니다. ( $n$ 이 홀수일 때마다 $x_{n+1}>x_{n}$ 인 사실은 관련이 없습니다.)
임의의 실수가 주어지면, 우리는 십진 근사를 취함으로써 해당 숫자에 수렴하는 수열을 쉽게 구성할 수 있을 것입니다. 예를 들어, 수열 $0.3,0.33,0.333,0.3333,...$ 은 $1/3$ 에 수렴합니다. 십진 표현(decimal representation) $0.3333...$ 은 이전 수열의 극한이며, 다음에 의해 정의되는 것에 주목하십시오:

0.3333...\triangleq \lim _{n\to \infty }\sum _{i=1}^{n}{\frac {3}{10^{i}}}

.

수열의 극한을 찾는 것은 항상 명확하지는 않습니다. 두 예제는 $\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$ (이것의 극한은 숫자 e입니다) 및 산술–기하 평균(arithmetic–geometric mean)입니다. 조임 정리(squeeze theorem)는 그러한 경우에서 종종 유용합니다.

Formal definition

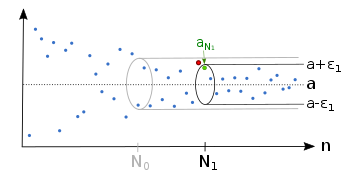
우리는, 만약 다음 조건을 유지하면, $x$ 를 수열(sequence) $(x_{n})$ 의 극한이라고 부릅니다:

각 실수 $\epsilon >0$ 에 대해, 모든 각 자연수 $n\geq N$ 에 대해, 우리가 $|x_{n}-x|<\epsilon$ 를 가지는 것을 만족하는 자연수 $N$ 이 존재합니다.

다시 말해서, 근점 $\epsilon$ 의 모든 각 측정에 대해, 수열의 항은 결국 극한에 가까워지는 것입니다. 수열 $(x_{n})$ 은, $x_{n}\to x$ 또는 $\lim _{n\to \infty }x_{n}=x$ 으로 쓰이는, 극한 $x$ 에 수렴한다 또는 경향이 있다라고 말합니다.

기호적으로, 이것은 다음입니다:

$\forall \varepsilon >0(\exists N\in \mathbb {N} (\forall n\in \mathbb {N} (n\geq N\implies |x_{n}-x|<\varepsilon ))).$

만약 수열이 어떤 극한에 수렴하면, 그것은 수렴입니다; 그렇지 않으면 그것은 발산입니다.

Illustration

극한 $a$ 에 수렴하는 수열의 예제.
$\varepsilon >0$ 에 관계없이, 수열은 나중에 엡실론 관 $(a-\varepsilon ,a+\varepsilon )$ 안에 완전하게 놓이도록, 인덱스 $N_{0}$ 가 있는 것을 우리는 가집니다.
더 작은 $\epsilon _{1}>0$ 에 대해 수열은 나중에 엡실론 관 $(a-\varepsilon _{1},a+\varepsilon _{1})$ 안에 있도록, 인덱스 $N_{1}$ 이 역시 있습니다.
각 $\varepsilon >0$ 에 대해 엡실론 관 밖에 오직 유한하게 많은 수열 구성원이 있습니다.

Properties

수열의 극한은 보통 산술 연산(arithmetic operations)과 관련하여 잘 작동합니다. 만약 $a_{n}\to a$ 와 $b_{n}\to b$ 이면, $a_{n}+b_{n}\to a+b$ , $a_{n}\cdot b_{n}\to ab$ 및, 만약 b도 임의의 $b_{n}$ 도 영이 아니면, ${\frac {a_{n}}{b_{n}}}\to {\frac {a}{b}}$ 입니다.

임의의 연속 함수(continuous function) f에 대해, 만약 $x_{n}\to x$ 이면 $f(x_{n})\to f(x)$ 입니다. 사실, 임의의 실수-값 함수(function) f가 연속인 것과 그것이 수열의 극한을 보존하는 것은 (비록 이것이 보다 연속성의 보다 일반적인 개념을 사용할 때 반드시 참일 필요는 없을지라도) 필요충분 조건입니다.

실수 수열의 극한의 일부 다른 중요한 속성은 다음을 포함합니다 (아래의 각 방정식에서, 오른쪽 변의 극한이 존재하는 것에서 제공됩니다).

수열의 극한은 고유합니다.
$\lim _{n\to \infty }(a_{n}\pm b_{n})=\lim _{n\to \infty }a_{n}\pm \lim _{n\to \infty }b_{n}$
$\lim _{n\to \infty }ca_{n}=c\cdot \lim _{n\to \infty }a_{n}$
$\lim _{n\to \infty }(a_{n}\cdot b_{n})=(\lim _{n\to \infty }a_{n})\cdot (\lim _{n\to \infty }b_{n})$
$\lim _{n\to \infty }\left({\frac {a_{n}}{b_{n}}}\right)={\frac {\lim \limits _{n\to \infty }a_{n}}{\lim \limits _{n\to \infty }b_{n}}}$ 여기서 $\lim _{n\to \infty }b_{n}\neq 0$
$\lim _{n\to \infty }a_{n}^{p}=\left[\lim _{n\to \infty }a_{n}\right]^{p}$
만약 어떤 $N$ 보다 더 큰 모든 $n$ 에 대해 $a_{n}\leq b_{n}$ 이면, $\lim _{n\to \infty }a_{n}\leq \lim _{n\to \infty }b_{n}$ 입니다.
(조임 정리) 만약 모든 $n>N$ 에 대해 $a_{n}\leq c_{n}\leq b_{n}$ 이고, $\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }b_{n}=L$ 이면, $\lim _{n\to \infty }c_{n}=L$ 입니다.
만약 수열이 경계지고(bounded) 단조적(monotonic)이면, 그것은 수렴합니다.
수열이 수렴하는 것과 모든 각 부분-수열이 수렴하는 것은 필요충분 조건입니다.
만약 수열의 모든 각 부분-수열이 같은 점에 수렴하는 그 자신의 부분-수열을 가지면, 원래 수열은 해당 점에 수렴합니다.

이들 속성은 성가신 공식 정의를 직접 사용할 필요없이 극한을 증명하기 위해 광범위하게 사용됩니다. 한번 ${\frac {1}{n}}\to 0$ 이 입증되면, 위의 속성을 사용하여, ${\frac {a}{b+{\frac {c}{n}}}}\to {\frac {a}{b}}$ , ( $b\neq 0$ )인 것을 보여주는 것이 쉽게 됩니다.

Infinite limits

만약, 모든 각 K에 대해, 모든 각 $n\geq N$ 에 대해, $x_{n}>K$ 를 만족하는 N이 있으면; 즉, 수열 항은 결국 임의의 고정된 K보다 더 커지면, 수열 $(x_{n})$ 은, $x_{n}\to \infty$ 또는 $\lim _{n\to \infty }x_{n}=\infty$ 으로 쓰이며, 무한대로 경향이 있다고 말합니다. 비슷하게, 만약 모든 각 K에 대해, 모든 각 $n\geq N$ 에 대해, $x_{n}<K$ 를 만족하는 N이 있으면, $x_{n}\to -\infty$ 입니다. 만약 수열이 무한대, 또는 음의 무한대로 경향이 있으면, 그것은 발산합니다 (어쨌든, 발산 수열이 반드시 양의 또는 음의 무한대로 경향이 있을 필요는 없습니다: 예를 들어, $x_{n}=(-1)^{n}$ 를 보십시오.)

Metric spaces

Definition

메트릭 공간(metric space) $(X,d)$ 의 점 $x$ 는, 만약 모든 $\epsilon >0$ 에 대해, 모든 각 $n\geq N$ 에 대해, $d(x_{n},x)<\epsilon$ 를 만족하는 $N$ 이 있으면, 수열(sequence) $(x_{n})$ 의 극한입니다. 이것은 $X=\mathbb {R}$ 및 $d(x,y)=|x-y|$ 일 때 실수에 대해 주어진 정의와 일치합니다.

Properties

임의의 연속 함수(continuous function) f에 대해, 만약 $x_{n}\to x$ 이면 $f(x_{n})\to f(x)$ 입니다. 사실, 함수(function) f가 연속인 것과 그것이 수열의 극한을 보존하는 것은 필요충분 조건입니다.

수열의 극한은 그들이 존재할 때 고유하며, 구별되는 점이 어떤 양의 거리에 의해 분리되기 때문에, 그래서 이 거리의 절반보다 작은 $\epsilon$ 에 대해, 수열 항은 양쪽 점의 거리 $\epsilon$ 안에 절대 있을 수 없습니다.

Topological spaces

Definition

토폴로지적 공간 (X, τ)의 점 x는, 만약 x의 모든 각 이웃(neighbourhood) U에 대해, 모든 각 $n\geq N$ 에 대해, $x_{n}\in U$ 을 만족하는 N이 있으면, 수열(sequence) (x_n)의 극한입니다. 이것은, 만약 (X,d)가 메트릭 공간이고 $\tau$ 가 d에 의해 생성된 토폴로지이면, 메트릭 공간에 대해 주어진 정의와 일치합니다.

토폴로지적 공간 T 안의 점들 $\left(x_{n}:n\in \mathbb {N} \right)\;$ 의 수열의 극한은 함수의 극한(limit of a function)의 특별한 경우입니다: 도메인은 아핀적으로 확장된 실수 시스템(affinely extended real number system)의 유도된 토폴로지(induced topology)를 갖는 공간 $\mathbb {N} \cup \lbrace +\infty \rbrace$ 안의 $\mathbb {N}$ 이며, 치역은 T이고, 함수 인수 n은 +∞로 경향이 있으며, 이것은 이 공간에서 $\mathbb {N}$ 의 극한 점(limit point)입니다.

Properties

만약 X가 하우스도르프 공간(Hausdorff space)이면 수열의 극한은, 그들이 존재하는 곳에서, 고유합니다. 이것은 일반적으로 경우가 될 필요는 없는 것에 주목하십시오; 특히, 만약 두 점 x와 y가 토폴로지적으로 구별-불가능(topologically indistinguishable)이면, x에 수렴하는 임의의 수열은 y에 반드시 수렴하고 그 반대도 마찬가지입니다.

Cauchy sequences

코시 수열은, 충분히 많은 초기 항이 버려진 후에, 그의 항이 함께 임의로 근접하게 궁극적으로 되는 수열입니다. 코시 수열의 개념은 메트릭 공간(metric spaces) 안의 수열의 연구, 및, 특히, 실수 해석학(real analysis)에서 중요합니다. 실수 해석학에서 특히 중요한 결과 중 하나는 수열의 수렴에 대해 코시 기준(Cauchy criterion for convergence of sequences)입니다: 실수의 수열이 수렴하는 것과 그것이 코시 수열인 것은 필요충분 조건입니다. 이것은 다른 완비 메트릭 공간(complete metric spaces)에서 역시 참으로 남습니다.

Definition in hyperreal numbers

초실수(hyperreal numbers)를 사용하여 극한의 정의는 인덱스의 "매우 큰" 값에 대해, 해당하는 항이 극한에 "매우 가깝다"는 직감을 공식화합니다. 보다 정확하게, 만약 모든 각 무한 초자연수(hypernatural) H에 대해, 항 x_H은 L에 무한하게 가까워지면, 즉, 차이 x_H − L가 무한소(infinitesimal)이면, 실수 수열 $(x_{n})$ 은 L에 경향이 있습니다. 동등하게, L은 x_H의 표준 부분(standard part)입니다:

L={\rm {st}}(x_{H}).\,

따라서, 극한은 다음 공식에 의해 정의될 수 있습니다:

\lim _{n\to \infty }x_{n}={\rm {st}}(x_{H}),

여기서 극한이 존재하는 것과 오른쪽 변이 무한 H의 선택에 독립적인 것은 필요충분 조건입니다.

Notes

^ ^a ^b Courant (1961), p. 29.
^ Courant (1961), p. 39.

Proofs

^ Proof: choose $N=1$ . For every $n\geq N$ , $|x_{n}-c|=0<\epsilon$
^ Proof: choose $N=\left\lfloor {\frac {1}{\epsilon }}\right\rfloor$ + 1 (the floor function). For every $n\geq N$ , $|x_{n}-0|\leq x_{N}={\frac {1}{\lfloor 1/\epsilon \rfloor +1}}<\epsilon$ .

References

Courant, Richard (1961). "Differential and Integral Calculus Volume I", Blackie & Son, Ltd., Glasgow.
Frank Morley and James Harkness A treatise on the theory of functions (New York: Macmillan, 1893)

External links

"Limit", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
A history of the calculus, including limits

[Courant_(1961),_p._29-1] Courant (1961), p. 29.

[2] Courant (1961), p. 39.

[3] Proof: choose $N=1$ . For every $n\geq N$ , $|x_{n}-c|=0<\epsilon$

[4] Proof: choose $N=\left\lfloor {\frac {1}{\epsilon }}\right\rfloor$ + 1 (the floor function). For every $n\geq N$ , $|x_{n}-0|\leq x_{N}={\frac {1}{\lfloor 1/\epsilon \rfloor +1}}<\epsilon$ .

[1]

[2]

[proof 1]

[proof 2]

History

Real numbers

Examples

Formal definition

Illustration

Properties

Infinite limits

Metric spaces

Definition

Properties

Topological spaces

Definition

Properties

Cauchy sequences

Definition in hyperreal numbers

See also

Notes

Proofs

References

External links