Limit of a function

Original article: w:Limit of a function

For the mathematical concept in general, see Limit (mathematics).

See also: Limit of a sequence and Limit point

$x$	${\frac {\sin x}{x}}$
1	0.841471...
0.1	0.998334...
0.01	0.999983...

Although the function (sin x)/x is not defined at zero, as x becomes closer and closer to zero, (sin x)/x becomes arbitrarily close to 1. In other words, the limit of (sin x)/x, as x approaches zero, equals 1.

수학(mathematics)에서, 함수의 극한(limit of a function)은 특정 입력(input) 근처에서 해당 함수(function)의 동작과 관련된 미적분학(calculus) 및 해석학(analysis)의 기본 개념입니다.

형식적인 정의는, 19세기 초반에 최초로 고안된 것으로, 아래에 제공됩니다. 비공식적으로, 함수 f는 모든 각 입력 x에 대한 출력(output) f(x)를 할당합니다. 우리는 f(x)가 x가 p에 점점 더 가까워지도록 움직일 때 L에 점점 더 가까워지면 함수가 입력 p에서 극한 L을 가짐을 말합니다. 보다 구체적으로, f가 p에 충분하게(sufficiently) 가까운 임의의 입력에 적용될 때, 출력 값은 임의적으로(arbitrarily) L에 근접하도록 강제됩니다. 다른 한편으로, 만약 p에 매우 가까운 일부 입력이 고정된 거리를 떨어져서 머무르는 출력에서 취해진다면, 우리는 극한이 존재하지 않는다라고 말합니다.

극한의 개념은 현대 미적분학(modern calculus)에서 많은 응용을 가집니다. 특히, 연속성(continuity)의 많은 정의는 극한의 개념을 사용합니다: 대략적으로 말하면, 함수는 만약 그의 극한의 모두가 함수의 값과 일치하면 연속입니다. 극한의 개념은 역시 도함수(derivative)의 정의에서 나타납니다: 하나의 변수의 미적분에서, 이것은 함수의 그래프에 대한 가름선(secant line)의 기울기(slope)의 극한하는 값입니다.

History

비록 17세기와 18세기의 미적분학의 개발에서 암시적이었을지라도, 함수의 극한의 현대적인 아이디어는 볼차노(Bolzano)로 거슬러 올라가며, 그는 1817년에 연속 함수를 정의하기 위해 엡실론-델타(epsilon-delta) 기법의 기초를 도입했습니다. 어쨌든, 그의 연구는 그의 삶 동안에는 알려지지 않았습니다.

코시(Cauchy)는 1821년에 발표된 그의 책 Cours d'analyse에서 x에서 무한소의 변화가 반드시 y에서 무한소의 변화를 일으킨다고 말함으로써 변수 양, 무한소(infinitesimal)와 극한을 논의하고, $y=f(x)$의 연속성을 정의했고, 반면에 (Grabiner 1983)은 증명에서 엡실론-델타 정의를 사용했다고 주장했습니다. 1861년에, 바이어슈트라스(Weierstrass)는 오늘날 보통 쓰이는 형식에서 극한의 엡실론-델타 정의를 처음으로 도입했습니다. 그는 역시 표기법 lim 및 lim_x→x0을 도입했습니다.

극한 기호 아래에 화살표를 놓는 현대 표기법은 1908년 그의 책 A Course of Pure Mathematics에서 하디(Hardy)에 기인합니다.

Motivation

$y=f(x)$의 그래프로 표현되는 풍경 위를 걷는 사람을 상상해 보십시오. 그들의 수평 위치는 x 값으로 측정되며, 이는 육지 지도 또는 전역적 위치 시스템(global positioning system)에 의해 제공되는 위치와 매우 유사합니다. 그들의 고도는 좌표 y에 의해 주어집니다. 그들은 x = p에 의해 주어진 수평 위치를 향해 걸어갑니다. 그들이 그것에 점점 더 가까워짐에 따라, 그들은 그들의 고도가 L에 가까워진다는 것을 알게 됩니다. 만약 x = p의 고도에 대해 물으면 그들은 그때에 L이라고 대답할 것입니다.

그렇다면 그들의 고도가 L에 접근한다고 말하는 것은 무엇을 의미할까요? 그것은 그들의 고도가 정확도에서 가능한 작은 오차를 제외하고는 L에 점점 더 가까워진다는 것을 의미합니다. 예를 들어, 우리는 여행자를 위해 특정 정확도 목표를 설정했다고 가정해 보겠습니다: 그들은 L의 십 미터 안에 반드시 있어야 합니다. 그들은 실제로 그들이 L의 십 수직 미터 안에 도달할 수 있다고 다시 보고하는데, 왜냐하면 그들은 그들이 p의 오십 수평 미터 이내에 있을 때, 그들의 고도는 항상 L으로부터 십 미터 이하라는 점에 주목하기 때문입니다.

정확도 목표는 그런-다음 변경됩니다: 그들은 일 수직 미터 안에 있을 수 있습니까? 네. 만약 그들이 p의 칠 수평 미터 안의 어디라고 있으면, 그들의 고도는 항상 목표 L으로부터 일 미터 안에 유지될 것입니다. 요약하면, 여행자의 고도가 그들의 수평 위치가 p에 가까워질 때 L에 가까워진다는 것은 모든 각 목표 정확도 결승점에 대해, 어쨌든 그것이 작을 수도 있지만, 그들의 고도가 해당 정확도 목표를 달성하는 p의 일부 이웃이 있음을 의미한다고 말하는 것입니다.

초기 비공식 명제는 이제 다음으로 설명될 수 있습니다:

함수 f(x)의 극한은 x가 p에 접근할 때 다음 속성을 갖는 숫자 L입니다: L로부터 임의의 목표 거리가 주어지면, f(x)의 값이 목표 거리 안에 유지되는 p로부터 거리가 있습니다.

사실, 이 명시적 명제는 토폴로지적 공간(topological space)에서 값을 갖는 함수의 극한의 형식적 정의에 상당히 가깝습니다.

보다 구체적으로, 다음임을 말하는 것은

$\lim _{x\to p}f(x)=L$,

ƒ(x)는 x에 충분히 가깝지만 p와 같지 않게 만듦으로써 L에 원하는 만큼 가깝게 만들 수 있다고 말하는 것입니다.

다음 정의는, (ε, δ)-정의로 알려져 있으며, 다양한 맥락에서 함수의 극한에 대해 일반적으로 허용되는 정의입니다.

Functions of a single variable

(ε, δ)-definition of limit

$f:\mathbb {R} \rightarrow \mathbb {R}$이 실수 직선(real line) 위에 정의된 함수이고, 두 개의 실수 p와 L이 있다고 가정합니다. 우리가 f의 극한은, x가 p에 접근함에 따라, L이다라고 말하고 다음과 같이 씁니다:

$\lim _{x\to p}f(x)=L$,

또는 대안적으로, f(x)가 x가 p가 되는 경향일 때 L이 되는 경향이다라고 말하고 다음과 같이 씁니다:

$f(x)\to L\;\;{\text{as}}\;\;x\to p$,

이때 다음 속성이 유지되어야 하는 조건에서 그렇습니다:

모든 각 실수 ε > 0에 대해, 모든 각 실수 x에 대해, 0 < |x − p| < δ가 |f(x) − L| < ε를 의미함을 만족하는 실수 δ > 0가 있습니다.

또는, 기호적으로:

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in \mathbb {R} )\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon )$.

예를 들어, 우리가 다음을 말할 수 있습니다:

$\lim _{x\to 2}4x+1=9$

왜냐하면 모든 각 실수 ε > 0에 대해, 우리는 모든 실수 x에 대해, 0 < |x − p| < δ이면, |f(x) − L| < ε가 되도록 δ = ε/4를 취할 수 있기 때문입니다.

보다 일반적인 정의는 실수 직선의 부분-집합(subsets) 위에 정의된 함수에 적용됩니다. (a, b)를 $\mathbb {R}$에서 열린 구간(open interval)이라고 놓고, 숫자 p를 (a, b)에 있다고 놓습니다. $f:S\to \mathbb {R}$을 p 자체를 제외하고 (a, b)의 모두를 포함하는 집합 S 위에 정의된 실수-값 함수(real-valued function)라고 놓습니다. 그런-다음 만약 다음이면 x가 p에 접근할 때 f의 극한이 L이라고 합니다:

모든 각 실수 ε > 0에 대해, 모든 x ∈ (a, b)에 대해, 0 < |x − p| < δ가 |f(x) − L| < ε임을 의미함을 만족하는 실수 δ > 0가 존재합니다.

보다, 기호적으로:

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon )$.

예를 들어, 우리는 다음을 말할 수 있습니다

$\lim _{x\to 1}{\sqrt {x+3}}=2$

왜냐하면 모든 각 실수 ε > 0에 대해, 우리는 모든 실수 x ≥ −3에 대해, 만약 0 < |x − 1| < δ이면, |f(x) − 2| < ε가 되도록 δ = ε를 취할 수 있기 때문입니다. 이 예제에서, S = [−3, ∞)는 점 1 주변의 열린 구간 (예를 들어, 구간 interval (0, 2))을 포함합니다.

여기서, 극한의 값은 p에서 정의되는 f에 의존하지 않고—만약 그것이 정의되면—값 f(p)에 의존하지 않는다는 점에 유의하십시오. 예를 들어,

$\lim _{x\to 1}{\frac {2x^{2}-x-1}{x-1}}=3$

왜냐하면 모든 각 ε > 0에 대해, 우리는 모든 실수 x ≠ 1에 대해, 0 < |x − 1| < δ이면, |f(x) − 3| < ε이 되도록 δ = ε/2를 취할 수 있기 때문입니다. 여기서 f(1)은 정의되지 않음에 주목하십시오.

문자 ε 및 δ는 "오차" 및 "거리"로 이해할 수 있습니다. 사실, 코시는 비록 연속성에 대한 그의 정의에서, 그가 ε 또는 δ가 아닌 무한소 $\alpha$를 사용했지만 일부 그의 연구에서 "오차"에 대한 약어로 ε를 사용했습니다 (Cours d'Analyse를 참조하십시오). 이들 용어에서, 극한에서 값의 측정에서 오류 (ε)는 극한 점까지의 거리 (δ)를 줄임으로써 원하는 만큼 작게 만들 수 있습니다. 아래에서 설명하는 것처럼, 이 정의는 역시 보다 일반적인 문맥에서 함수에 대해 동작합니다. δ와 ε가 거리를 나타낸다는 아이디어는 이들 일반화를 제안하는 데 도움이 됩니다.

Existence and one-sided limits

Main article: One-sided limit

The limit as: x → x₀⁺ ≠ x → x₀⁻. Therefore, the limit as x → x₀ does not exist.

대안적으로, x는 위 (오른쪽) 또는 아래 (왼쪽)에서 p에 접근할 수 있으며, 그 경우에서, 극한은 각각 다음으로 쓸 수 있습니다:

$\lim _{x\to p^{+}}f(x)=L$

또는

$\lim _{x\to p^{-}}f(x)=L$

만약 이들 극한이 p에서 존재하고 그곳에서 같으면, 이것은 p에서 f(x)의 극한으로 참조될 수 있습니다. 만약 한쪽 극한이 p에서 존재하지만, 같지 않으면, p에는 극한은 없습니다 (즉, p에서 극한은 존재하지 않습니다). 만약 한쪽 극한 중에 하나라도 p에서 존재하지 않으면, p에서 극한은 역시 존재하지 않습니다.

형식적인 정의는 다음과 같습니다. 만약, 다음이면 f의 극한은 x가 위로부터 p에 접근할 때 L입니다:

모든 각 ε > 0에 대해, 0 < x − p < δ일 때마다, 우리가 |f(x) − L| < ε를 가짐을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<x-p<\delta \implies |f(x)-L|<\varepsilon )$.

만약 다음이면 f의 극한은 x가 아래로부터 p에 접근할 때 L입니다:

모든 각 ε > 0에 대해, 0 < p − x < δ일 때마다, 우리가 |f(x) − L| < ε를 가짐을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<p-x<\delta \implies |f(x)-L|<\varepsilon )$.

만약 극한이 존재하지 않으면, p에서 f의 진동(oscillation)은 비-영입니다.

More general subsets

열린 구간과는 별개로, 극한은 다음처럼 R의 임의적인 부분-집합 위에 함수에 대해 정의될 수 있습니다 (Bartle & Sherbert 2000): $f:S\to \mathbb {R}$를 임의적인 $S\subseteq \mathbb {R}$ 위에 정의된 실수-값 함수라고 놓습니다. p를 S의 극한 점(limit point)으로 놓습니다—즉, p는 p와 구별되는 S의 원소의 일부 수열의 극한입니다. 그런-다음 우리는 f의 극한은, x가 S에서 값으로부터 p에 접근할 때 L이다라고 말하고 다음과 같이 씁니다:

$\lim _{\begin{smallmatrix}x\to p\\x\in S\end{smallmatrix}}f(x)=L$

이때, 다음이 유지되어야 한다는 조건으로 그렇습니다:

모든 각 ε > 0에 대해, 모든 각 x ∈ S에 대해, 0 < |x − p| < δ가 |f(x) − L| < ε임을 의미함을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon )$.

f가 S 위에 정의된다는 조건은 S가 f의 도메인의 부분-집합이라는 것입니다. 이 일반화는 구간 위에 특별한 경우 극한을 포함하며, 마찬가지로 실수-값 함수의 왼-쪽 극한 (예를 들어, S를 형식 $(-\infty ,a)$의 열린 구간이도록 취함으로써), 및 오른-쪽 극한 (예를 들어, S를 형식 $(a,\infty )$의 열린 구간이도록 취함으로써)을 포함합니다. 그것은 역시 한쪽 극한의 개념을 (반-)닫힌 구간의 포함된 끝점으로 확장하므로, 제곱근 함수(Square root function) f(x)=√x는 x가 위로부터 0에 접근할 때 극한 0을 가질 수 있습니다:

$\lim _{\begin{smallmatrix}x\to 0\\x\in [0,\infty )\end{smallmatrix}}{\sqrt {x}}=0$

왜냐하면 모든 각 ε > 0에 대해, 우리는 모든 x ≥ 0에 대해, 0 < |x − 0| < δ이면, |f(x) − 0| < ε임을 만족하는 δ = ε를 취할 수 있기 때문입니다.

Deleted versus non-deleted limits

여기에 주어진 극한의 정의는 f가 p에서 정의되는 방법 (또는 여부)에 의존하지 않습니다. Bartle (1967)은 이것을 삭제된 극한(deleted limit)으로 참조하는데, 왜냐하면 그것은 p에서 f의 값을 제외하기 때문입니다. 대응하는 비-삭제된 극한(non-deleted limit)은 p가 f의 도메인에 있으면 p에서 f의 값에 따라 달라집니다. $f:S\to \mathbb {R}$을 실수-값 함수라고 놓습니다. 만약 다음이면 f의 비-삭제된 극한은, x가 p에 접근할 때 L입니다:

모든 각 ε > 0에 대해, 모든 x ∈ S에 대해, |x − p| < δ가 |f(x) − L| < ε임을 의미함을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(|x-p|<\delta \implies |f(x)-L|<\varepsilon )$.

그 정의는, 이웃 | x − p | < δ은 이제 점 p를 포함하는 것을 제외하고, 대조적으로 삭제된 이웃(deleted neighborhood) 0 < | x − p | < δ과 같습니다. 이것은 비-삭제된 극한의 정의를 덜 일반적으로 만듭니다. 비-삭제된 극한과 작동하는 이점 중 하나는 (그들 비-삭제된 극한의 존재 이외의) 함수에 대한 임의의 제약 없이 합성의 극한에 대한 정리를 말하는 것을 허용한다는 것입니다 (Hubbard (2015)).

Bartle (1967)는 비록 "극한"에 의해 일부 저자가 이것을 비-삭제된 극한으로 의미할지라도, 삭제된 극한이 가장 인기있는 것에 주목합니다. 예를 들어, Apostol (1974), Courant (1924), Hardy (1921), Rudin (1964), Whittaker & Watson (1902) 모두는 삭제된 극한을 의미하기 위해 "극한"을 취합니다.

Examples

Non-existence of one-sided limit(s)

The function without a limit, at an essential discontinuity

다음 함수는

$f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\text{ for }}x<1\\0&{\text{ for }}x=1\\{\frac {0.1}{x-1}}&{\text{ for }}x>1\end{cases}}$

$x_{0}=1$에서 극한을 가지지 않지만 (왼-쪽 극한은 사인 함수의 진동 본성에 기인하여 존재하지 않고, 오른-쪽 극한은 역수 함수의 점근적 행위에 기인하여 존재하지 않습니다), 모든 각 다른 x-좌표에서 극한을 가집니다.

다음 함수는

$f(x)={\begin{cases}1&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}$

(일명, 디리클레 함수(Dirichlet function))는 임의의 x-좌표에서 극한을 가지지 않습니다.

Non-equality of one-sided limits

다음 함수는

$f(x)={\begin{cases}1&{\text{ for }}x<0\\2&{\text{ for }}x\geq 0\end{cases}}$

모든 각 비-영 x-좌표에서 극한을 가집니다 (극한은 음의 x에 대해 1과 같고 양의 x에 대해 2와 같습니다). x = 0에서 극한은 존재하지 않습니다 (왼-쪽 극한은 1과 같고, 반면에 오른-쪽 극한은 2와 같습니다).

Limits at only one point

다음 함수와

$f(x)={\begin{cases}x&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}$

다음 함수는

$f(x)={\begin{cases}|x|&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}$

둘 다 x = 0에서 극한을 가지고 그것은 0과 같습니다.

Limits at countably many points

다음 함수는

$f(x)={\begin{cases}\sin x&x{\text{ irrational }}\\1&x{\text{ rational }}\end{cases}}$

형식 ${\frac {\pi }{2}}+2n\pi$의 임의의 x-좌표에서 극한을 가지며, 여기서 n음 임의의 정수입니다.

Limits involving infinity

Limits at infinity

The limit of this function at infinity exists.

$f:S\to \mathbb {R}$를 $S\subseteq \mathbb {R}$ 위에 정의된 함수라고 놓습니다. f의 극한은 x가 무한대에 접근할 때 L이다는, 다음으로 표시되며

$\lim _{x\to \infty }f(x)=L$,

다음임을 의미합니다:

모든 각 ε > 0에 대해, x > c일 때마다, 우리가 |f(x) − L| < ε를 가짐을 만족하는 c > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(x>c\implies |f(x)-L|<\varepsilon )$.

유사하게, f의 극한은 x가 음의 무한대로 접근할 때 L이다는, 다음으로 표시되며

$\lim _{x\to -\infty }f(x)=L$,

다음임을 의미합니다:

모든 각 ε > 0에 대해, x < −c일 때마다, 우리가 |f(x) − L| < ε를 가짐을 만족하는 c > 0가 존재합니다.$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(x<-c\implies |f(x)-L|<\varepsilon )$.

예를 들어,

$\lim _{x\to \infty }\left(-{\frac {3\sin x}{x}}+4\right)=4$

왜냐하면 모든 각 ε > 0에 대해, 우리는 모든 실수 x에 대해, x > c이면, |f(x) − 4| < ε임을 만족하는 c = 3/ε를 취할 수 있기 때문입니다.

또 다른 예제는 다음입니다:

$\lim _{x\to -\infty }e^{x}=0$

왜냐하면 모든 각 ε > 0에 대해, 우리는 모든 실수 x에 대해, x < −c이면, |f(x) − 0| < ε임을 만족하는 c = max{1, −ln(ε)}를 취할 수 있기 때문입니다.

Infinite limits

경계 없이 값이 증가하는 함수에 대해, 그 함수는 발산하고 보통의 극한은 존재하지 않습니다. 어쨌든, 이 경우에서, 무한 값으로 극한을 도입할 수 있습니다.

$f:S\to \mathbb {R}$를 $S\subseteq \mathbb {R}$ 위에 정의된 함수라고 놓습니다. 명제 f의 극한은 x가 p로 접근할 때 무한대이다는, 다음과 같이 표시되며

$\lim _{x\to p}f(x)=\infty ,$

다음임을 의미합니다:

모든 각 N > 0에 대해, 0 < |x − p| < δ일 때마다, 우리가 f(x) > N을 가짐을 만족하는 δ > 0가 존재합니다.

$(\forall N>0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies f(x)>N)$.

명제 f의 극한은 x가 p로 접근할 때 음의 무한대이다는, 다음으로 표시되며

$\lim _{x\to p}f(x)=-\infty ,$

다음임을 의미합니다:

모든 각 N > 0에 대해, 0 < |x − p| < δ일 때마다, 우리가 f(x) < −N을 가짐을 만족하는 δ > 0가 존재합니다.

$(\forall N>0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies f(x)<-N)$.

예를 들어,

$\lim _{x\to 1}{\frac {1}{(x-1)^{2}}}=\infty$

왜냐하면 모든 각 N > 0에 대해, 우리가 모든 실수 x > 0에 대해, 0 < x − 1 < δ이면, f(x) > N임을 만족하는 δ = 1/√N를 취할 수 있기 때문입니다.

이들 아이디어는 자연스러운 방법으로 결합되어 다음과 같은 다양한 조합에 대한 정의를 생성할 수 있습니다:

$\lim _{x\to \infty }f(x)=\infty$, or $\lim _{x\to p^{+}}f(x)=-\infty$.

예를 들어,

$\lim _{x\to 0^{+}}\ln x=-\infty$

왜냐하면 모든 각 N > 0에 대해, 우리가 모든 실수 x > 0에 대해, 0 < x − 0 < δ이면, f(x) < −N임을 만족하는 δ = e^−N를 취할 수 있기 때문입니다.

무한대를 포함하는 극한은 점근선(asymptotes)의 개념과 연결됩니다.

극한의 이들 개념은 무한대에서 극한에 메트릭 공간 해석을 제공하려고 시도합니다. 사실, 그것들은 다음이면 극한의 토폴로지적 공간 정의와 일치합니다:

• $-\infty$의 이웃은 일부 c ∈ R에 대해 구간(interval) [−∞, c)을 포함하기 위해 정의되고,
• $\infty$의 이웃은 일부 c ∈ R에 대해 구간 (c, ∞]을 포함하기 위해 정의되고,
• a ∈ R의 이웃은 정규 방법 메트릭 공간 R에서 정의됩니다.

이 경우에서, R은 토폴로지적 공간이고 X, Y⊆ R을 갖는 형식 f: X → Y의 모든 함수는 극한의 토폴로지적 정의를 따릅니다. 이 토폴로지적 정의와 함께, 위에 메트릭 의미에서 정의되지 않은 유한 점에서 무한 극한을 쉽게 정의할 수 있습니다.

Alternative notation

많은 저자들은 투영적으로 확장된 실수 직선(projectively extended real line)을 확장된 실수 직선(extended real line)뿐만 아니라 무한 값을 포함하는 방법으로 사용되는 것을 허용합니다. 이 표기법과 함께, 확장된 실수 직선은 R ∪ {−∞, +∞}로 주어지고 투영적으로 확장된 실수 직선은, ∞의 이웃이 형식 {x: |x| > c}의 집합인, R ∪ {∞}입니다. 이점은 우리가 모든 경우를 덮기 위해 극한 (왼쪽, 오른쪽, 및 중앙)에 대해 오직 세 정의가 필요하다는 것입니다. 위의 제시된 것처럼, 완전하게 엄격한 계정에 대해, 우리는 무한대의 각 조합 (다섯 방향: −∞, 왼쪽, 중앙, 오른쪽, 및 +∞; 세 경계: −∞, 유한, 또는 +∞)에 대해 15개의 개별적인 경우를 고려하는 것이 필요할 것입니다. 주목할만한 함정이 역시 있습니다. 예를 들어, 확장된 실수 직선과 함께 작동할 때, $x^{-1}$는 중앙 극한을 보유할 수 없습니다 (이것이 정규입니다):

$\lim _{x\to 0^{+}}{1 \over x}=+\infty ,\lim _{x\to 0^{-}}{1 \over x}=-\infty$.

대조적으로, 투영적 실수 직선과 함께 작동할 때, 무한대 (0과 매우 비슷하게)는 부호가 없으므로, 중앙 극한은 해당 문맥에서 존재합니다:

$\lim _{x\to 0^{+}}{1 \over x}=\lim _{x\to 0^{-}}{1 \over x}=\lim _{x\to 0}{1 \over x}=\infty$.

사실 사용에서 형식적인 시스템과 많은 충돌이 있습니다. 수치적 미분화와 적분화의 특정 응용에서, 예를 들어, 부호화된 영(signed zeroes)을 가지는 것이 편리합니다. 간단한 이유는 $\lim _{x\to 0^{-}}{x^{-1}}=-\infty$의 전환과 함께 수행해야 하며, 즉, $\lim _{x\to -\infty }{x^{-1}}=-0$에 대해 참을 고려하는 것이 편리합니다. 그러한 영은 무한소(infinitesimal)에 대한 근사로 이해될 수 있습니다.

Limits at infinity for rational functions

Horizontal asymptote about y = 4

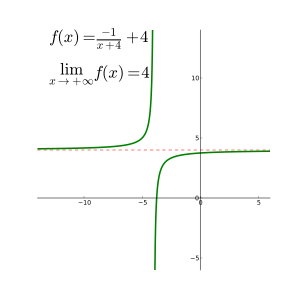
유리 함수(rational function) f(x) = p(x)/q(x)에 대해 무한대에서 극한을 평가하는 데 다음과 같은 세 기본 규칙이 있습니다: (여기서 p와 q는 다항식입니다):

• 만약 p의 차수(degree)가 q의 차수보다 크면, 극한은 선행 계수의 부호를 따르는 양 또는 음의 무한대입니다;
• 만약 p와 q의 차수가 같으면, 극한은 p의 선행 계수를 q의 선행 계수로 나눈 것입니다;
• 만약 p의 차수가 q의 차수보다 작으면, 극한은 0입니다.

만약 무한대에서 극한이 존재하면, 그것은 y = L에서 수평 점근선을 나타냅니다. 다항식은 수평 점근선을 가지지 않습니다; 그런 점근선은 어쨌든 유리 함수와 함께 나타날 수 있습니다.

Functions of more than one variable

Ordinary limits

|x − p|가 거리(distance)를 나타냄을 주목함으로써, 극한의 정의는 둘 이상의 변수의 함수로 확장될 수 있습니다. $S\times T\subseteq \mathbb {R} ^{2}$ 위에 정의된 함수 $f:S\times T\to \mathbb {R}$의 경우에서, 우리는 극한을 다음과 같이 정의했습니다: f의 극한은 (x, y)가 (p, q)에 접근할 때 L이다는 다음과 같이 씁니다

$\lim _{(x,y)\to (p,q)}f(x,y)=L$

이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

모든 각 ε > 0에 대해, S에서 모든 x와 T에서 모든 y에 대해, 0 < √(x−p)² + (y−q)² < δ일 때마다, 우리가 |f(x, y) − L| < ε를 가짐을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,(0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta \implies |f(x,y)-L|<\varepsilon )$.

여기서 √(x−p)² + (y−q)²는 (x, y)와 (p, q) 사이의 유클리드 거리(Euclidean distance)입니다. (이것은 사실 임의의 노름(norm) ||(x, y) − (p, q)||에 의해 대체될 수 있고, 임의의 개수의 변수로 확장될 수 있습니다.)

예를 들어, 우리는 다음을 말할 수 있습니다:

$\lim _{(x,y)\to (0,0)}{\frac {x^{4}}{x^{2}+y^{2}}}=0$

왜냐하면 모든 각 ε > 0에 대해, 우리는 모든 실수 x ≠ 0와 모든 실수 y ≠ 0에 대해, 0 < √(x−0)² + (y−0)² < δ이면, |f(x, y) − 0| < ε임을 만족하는 δ = √ε를 취할 수 있기 때문입니다.

단일 변수의 경우와 유사하게, (p, q)에서 f의 값은 이 극한의 정의에서 중요하지 않습니다.

그러한 다변수 극한이 존재하기 위해, 이 정의는 (p, q)에 접근하는 모든 각 가능한 경로를 따라 f의 값이 L에 접근해야 함을 요구합니다. 위의 예제에서, 다음 함수는 조건을 만족시킵니다:

$f(x,y)={\frac {x^{4}}{x^{2}+y^{2}}}$

이것은 극 좌표(polar coordinates) (x, y) = (r cos(θ), r sin(θ)) → (0, 0)을 고려함으로써 알 수 있으며, 이는 다음을 제공합니다:

$\lim _{r\to 0}f(r\cos \theta ,r\sin \theta )=\lim _{r\to 0}{\frac {r^{4}\cos ^{4}\theta }{r^{2}}}=\lim _{r\to 0}r^{2}\cos ^{4}\theta$.

여기서 θ = θ(r)는 f가 (p, q)에 접근하는 경로를 따라 경로의 모양을 제어하는 r의 함수입니다. cos(θ)는 샌드위치 정리(sandwich theorem)에 의해 [−1, 1] 사이에 경계지기 때문에, 이 극한은 0이 되는 경향이 있습니다.

대조적으로, 다음 함수는

$f(x,y)={\frac {xy}{x^{2}+y^{2}}}$

(0, 0)에서 극한을 가지지 않습니다. 경로 (x, y) = (t, 0) → (0, 0)를 취하면, 우리는 다음을 얻습니다:

$\lim _{t\to 0}f(t,0)=\lim _{t\to 0}{\frac {0}{t^{2}}}=0$,

반면에 경로 (x, y) = (t, t) → (0, 0)를 취하면, 우리는 다음을 얻습니다:

$\lim _{t\to 0}f(t,t)=\lim _{t\to 0}{\frac {t^{2}}{t^{2}+t^{2}}}={\frac {1}{2}}$.

두 값이 일치하지 않기 때문에, f는 (x, y)가 (0, 0)에 접근할 때 딘일 값으로 경향을 갖지 않습니다.

Multiple limits

비록 덜 일반적으로 사용되지만, 다변수 함수에 대한 또 다른 유형의 극한이 있으며, 다중 극한(multiple limit)으로 알려져 있습니다. 두-변수 함수에 대해, 이것은 이중 극한(double limit)입니다. $f:S\times T\to \mathbb {R}$를 $S\times T\subseteq \mathbb {R} ^{2}$ 위에 정의되는 것으로 놓고, 우리가 f의 이중 극한은 x가 p에 접근하고 y가 q에 접근할 때 L이다라고 말하며, 다음과 같이 씁니다:

$\lim _{\begin{smallmatrix}x\to p\\y\to q\end{smallmatrix}}f(x,y)=L$

이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

모든 각 ε > 0에 대해, S에서 모든 x와 T에서 모든 y에 대해, 0 < |x − p| < δ와 0 < |y−q| < δ일 때마다, 우리가 |f(x, y) − L| < ε를 가짐을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,((0<|x-p|<\delta )\land (0<|y-q|<\delta )\implies |f(x,y)-L|<\varepsilon )$.

그러한 이중 적분이 존재하기 위해, 이 정의는 두 직선 x = p와 y = q를 제외하고 (p, q)에 접근하는 모든 각 가능한 경로를 따라 L에 접근하는 f의 값을 요구합니다. 결과로써, 다중 극한은 보통 극한보다 약한 개념입니다: 만약 보통 극한이 존재하고 L과 같으면, 다중 극한이 존재하고 역시 L과 같습니다. 그 전환은 참이 아님을 주목하십시오: 다중 극한의 존재가 보통 극한의 존재를 의미하지 않습니다. 다음 예제를 생각해 보십시오:

$f(x,y)={\begin{cases}1\quad {\text{for}}\quad xy\neq 0\\0\quad {\text{for}}\quad xy=0\end{cases}}$

여기서 다음이지만,

$\lim _{\begin{smallmatrix}x\to 0\\y\to 0\end{smallmatrix}}f(x,y)=1$

다음입니다:

$\lim _{(x,y)\to (0,0)}f(x,y)$ does not exists.

만약 f의 도메인이 $(S\setminus \{p\})\times (T\setminus \{q\})$로 제한되면, 극한의 두 정의는 일치합니다.

Multiple limits at infinity

다중 극한의 개념은 단일 변수 함수의 개념과 유사한 방법에서 무한대에서 극한으로 확장될 수 있습니다. $f:S\times T\to \mathbb {R}$에 대해, 우리가 f의 이중 극한은 x와 y가 무한대에 접근할 때 L이다라고 말하며, 다음과 같이 씁니다:

$\lim _{\begin{smallmatrix}x\to \infty \\y\to \infty \end{smallmatrix}}f(x,y)=L$

이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

모든 각 ε > 0에 대해, S에서 모든 x와 y에 대해, x > c와 y > c일 때마다, 우리가 |f(x, y) − L| < ε를 가짐을 만족하는 c > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(\forall y\in T)\,((x>c)\land (y>c)\implies |f(x,y)-L|<\varepsilon )$.

우리가 f의 이중 적분은 as x와 y가 음의 무한대에 접근할 때 L이다라고 말하며, 다음과 같이 씁니다:

$\lim _{\begin{smallmatrix}x\to -\infty \\y\to -\infty \end{smallmatrix}}f(x,y)=L$

이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

모든 각 ε > 0에 대해, S에서 모든 x와 T에서 모든 y에 대해,, x < −c와 y < −c일 때마다, 우리가 |f(x, y) − L| < ε를 가짐을 만족하는 c > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(\forall y\in T)\,((x<-c)\land (y<-c)\implies |f(x,y)-L|<\varepsilon )$.

Pointwise limits and uniform limits

Main articles: Pointwise convergence and Uniform convergence

$f:S\times T\to \mathbb {R}$라고 놓습니다. (x, y) → (p, q)일 때 극한을 취하는 대신, 우리는 y의 단일-변수 함수, 즉 $g:T\to \mathbb {R}$를 얻기 위해 단 하나의 변수, 말하자면, x → p의 극한을 취하는 것을 고려할 수 있습니다. 실제로, 이 극한하는 과정은 두 가지 구별되는 방법으로 수행될 수 있습니다. 첫 번째 하나는 점별 극한(pointwise limit)이라고 불립니다. 우리는 f의 점별 극한이 x가 p에 접근할 때 g이다라고 말하며, 다음과 같이 나타냅니다:

$\lim _{x\to p}f(x,y)=g(y)$, 또는

$\lim _{x\to p}f(x,y)=g(y)\;\;{\text{pointwise}}$.

대안적으로, 우리는 f는 x가 p에 접근할 때 점별로 g로 가는 경향이 있다라고 말하며, 다음과 같이 표시합니다:

$f(x,y)\to g(y)\;\;{\text{as}}\;\;x\to p$, 또는

$f(x,y)\to g(y)\;\;{\text{pointwise}}\;\;{\text{as}}\;\;x\to p$.

이 극한은 다음이 유지되면 존재합니다:

모든 각 ε > 0와 T에서 모든 각 고정된 y에 대해, S에서 모든 x에 대해, 0 < |x − p| < δ일 때마다, 우리가 |f(x, y) − g(y)| < ε를 가짐을 만족하는 δ(ε, y) > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\forall y\in T)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies |f(x,y)-g(y)|<\varepsilon )$.

여기서, δ = δ(ε, y)는 ε와 y 둘 다의 함수입니다. 각 δ는 y의 특정 점(specific point)에 대해 선택됩니다. 그러므로 우리는 극한이 y에서 점별이라고 말합니다. 예를 들어, 다음은

$f(x,y)={\frac {x}{\cos y}}$

다음 상수 영 함수의 점별 극한을 가집니다:

$\lim _{x\to 0}f(x,y)=0(y)\;\;{\text{pointwise}}$

왜냐하면 모든 각 고정된 y에 대해, 그 극한은 분명히 0입니다. 만약 y가 고정되지 않으면 이 논증은 실패함을 주목하십시오: 만약 y가 π/2에 매우 가까우면, 분수 값이 0에서 벗어날 수 있습니다.

이것은 극한의 또 다른 정의, 즉 균등 극한(uniform limit)으로 이어집니다. 우리는 T 위에 f의 균등 극한이 x가 p에 접근할 때 g이다라고 말하며, 다음과 같이 나타냅니다:

${\underset {\begin{smallmatrix}x\to p\\y\in T\end{smallmatrix}}{\mathrm {unif} \lim \;}}f(x,y)=g(y)$, 또는

$\lim _{x\to p}f(x,y)=g(y)\;\;{\text{uniformly on}}\;T$.

대안적으로, 우리는 f는 x가 p에 접근할 때 T 위에 균등하게 g로 가는 경향이 있다라고 말할 수 있으며, 다음과 같이 나타냅니다:

$f(x,y)\rightrightarrows g(y)\;{\text{on}}\;T\;\;{\text{as}}\;\;x\to p$, 또는

$f(x,y)\to g(y)\;\;{\text{uniformly on}}\;T\;\;{\text{as}}\;\;x\to p$.

이 극한은 만약 다음이 유지되면 존재합니다:

모든 각 ε > 0에 대해, S에서 모든 x와 T에서 모든 y에 대해, 0 < |x − p| < δ일 때마다, 우리가 |f(x, y) − g(y)| < ε를 가짐을 만족하는 δ(ε) > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,(0<|x-p|<\delta \implies |f(x,y)-g(y)|<\varepsilon )$.

여기서, δ = δ(ε)는 오직 ε의 함수이지만 y의 함수는 아닙니다. 다른 말로, δ는 T에서 모든 y로 균등하게 적용-가능(uniformly applicable)입니다. 그러므로 우리는 그 극한이 y에서 균등이라고 말할 수 있습니다. 예를 들어, 다음은

$f(x,y)=x\cos y$

다음 상수 영 함수의 균등 극한을 가집니다:

$\lim _{x\to 0}f(x,y)=0(y)\;\;{\text{ uniformly on}}\;\mathbb {R}$

왜냐하면 모든 실수 y에 대해, cos(y)는 [−1, 1] 사이에 경계지기 때문입니다. 그러므로 y가 어떻게 동작하든, 우리는 샌드위치 정리(sandwich theorem)를 사용하여 극한이 0임을 보여줄 수 있습니다.

Iterated limits

Main article: Iterated limits

$f:S\times T\to \mathbb {R}$라고 놓습니다. 우리는 y의 단일-변수 함수, 즉 $g:T\to \mathbb {R}$을 얻기 위해 단 하나의 변수, 말하자면, x → p의 극한을 취하는 것을 고려할 수 있고, 그런-다음 나머지 변수, 즉 y → q에서 극한을 취하여 숫자 L을 얻을 수 있습니다. 기호적으로,

$\lim _{y\to q}\lim _{x\to p}f(x,y)=\lim _{y\to q}g(y)=L$.

이 극한은 다변수 함수의 반복된 극한(iterated limit)으로 알려져 있습니다. 극한을 취하는 순서는 결과에 영향을 줄 수 있음을 주목하십시오, 즉,

$\lim _{y\to q}\lim _{x\to p}f(x,y)\neq \lim _{x\to p}\lim _{y\to q}f(x,y)$ in general.

무어-오스굿 정리(Moore-Osgood theorem)에 의해 상등의 충분 조건이 제공되며, 이는 극한 $\lim _{x\to p}f(x,y)=g(y)$가 T 위에 균등할 것을 요구합니다.

Functions on metric spaces

M과 N이, 각각, 메트릭 공간(metric spaces) A와 B의 부분-집합이고, x ∈ M, p는 M의 극한 점(limit point)이고 L ∈ N을 갖는, f : M → N은 M과 N 사이에서 정의된다고 가정합니다. f의 극한은 x가 p에 접근할 때 L이다라고 말하고, 다음과 같이 씁니다:

$\lim _{x\to p}f(x)=L$

이때 만약 다음 속성을 보유해야 합니다:

모든 각 ε > 0에 대해, 모든 점 x ∈ M에 대해, 0 < d_A(x, p) < δ가 d_B(f(x), L) < ε를 의미함을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in M)\,(0<d_{A}(x,p)<\delta \implies d_{B}(f(x),L)<\varepsilon )$.

다시-한번, p는 f의 도메인 안에 있을 필요가 없고, L은 f의 치역 안에 있어야 할 필요도 없고, 심지어 f(p)가 정의되더라도 그것이 L과 같을 필요는 없다는 점에 주목하십시오.

Euclidean metric

유클리드 공간(Euclidean space)에서 극한은 벡터-값 함수(vector-valued functions)로의 극한의 직접적인 일반화입니다. 예를 들어, 다음을 만족하는 함수 $f:S\times T\to \mathbb {R} ^{3}$를 고려할 수 있습니다:

$f(x,y)=(f_{1}(x,y),f_{2}(x,y),f_{3}(x,y))$.

그런-다음, 보통의 유클리드 메트릭(Euclidean metric) 아래에서,

$\lim _{(x,y)\to (p,q)}f(x,y)=(L_{1},L_{2},L_{3})$

이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

모든 각 ε > 0에 대해, S에서 모든 x와 T에서 모든 y에 대해, 0 < √(x−p)² + (y−q)² < δ가 √(f₁−L₁)² + (f₂−L₂)² + (f₃−L₃)² < ε를 의미함을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,(0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta \implies {\sqrt {(f_{1}-L_{1})^{2}+(f_{2}-L_{2})^{2}+(f_{3}-L_{3})^{2}}}<\varepsilon )$.

이 예제에서, 관련된 함수는 유한-차원(dimension) 벡터-값 함수입니다. 이 경우에서, 벡터-값 함수에 대한 극한 정리는 각 구성 요소의 극한이 존재하면, 벡터-값 함수의 극한은 각 구성 요소가 극한을 취한 벡터와 같다고 말합니다:

$\lim _{(x,y)\to (p,q)}\left(f_{1}(x,y),f_{2}(x,y),f_{3}(x,y)\right)=\left(\lim _{(x,y)\to (p,q)}f_{1}(x,y),\lim _{(x,y)\to (p,q)}f_{2}(x,y),\lim _{(x,y)\to (p,q)}f_{3}(x,y)\right)$.

Manhattan metric

우리는 역시 유클리드 공간 이외의 공간을 고려하고 싶을 수도 있습니다. 예를 들어 맨해튼 공간이 있습니다. 다음을 만족하는 $f:S\to \mathbb {R} ^{2}$를 생각해 보십시오:

$f(x)=(f_{1}(x),f_{2}(x))$.

그런-다음, 맨해튼 메트릭(Manhattan metric) 아래에서,

$\lim _{x\to p}f(x)=(L_{1},L_{2})$

이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

모든 각 ε > 0에 대해, S에서 모든 x에 대해, 0 < |x − p| < δ가 |f₁−L₁| + |f₂−L₂| < ε를 의미함을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies |f_{1}-L_{1}|+|f_{2}-L_{2}|<\varepsilon )$.

이것은 역시 유한-차원 벡터-값 함수이기 때문에, 위에서 설명한 극한 정리도 적용됩니다.

Uniform metric

마지막으로, 무한 차원을 가지는 함수 공간(function space)에서 극한에 대해 논의할 것입니다. 함수 공간 $S\times T\to \mathbb {R}$에서 함수 f(x, y)를 생각해 보십시오. 우리는 x가 p에 접근할 때, f(x, y)가 함수 공간 $T\to \mathbb {R}$에 있는 또 다른 함수 g(y)로 향하는 방법을 알고 싶을 것입니다. 이 기능 공간에서 "근접성"은 균등 메트릭(uniform metric) 아래에서 측정될 수 있습니다. 그런-다음, 우리는 T 위에 f의 균등 극한이 x가 p에 접근할 때 g이다라고 말하고 다음과 같이 쓸 것입니다:

${\underset {\begin{smallmatrix}x\to p\\y\in T\end{smallmatrix}}{\mathrm {unif} \lim \;}}f(x,y)=g(y)$, 또는

$\lim _{x\to p}f(x,y)=g(y)\;\;{\text{uniformly on}}\;T$, 이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

모든 각 ε > 0에 대해, S에서 모든 x에 대해, 0 < |x − p| < δ가 sup_y∈T |f(x,y) − g(y)| < ε를 의미함을 만족하는 δ > 0가 존재합니다.

$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies \sup _{y\in T}|f(x,y)-g(y)|<\varepsilon )$.

사실, 이 정의는 이전 절에서 소개한 다변수 함수의 균등 극한과 동등하다는 것을 알 수 있습니다.

Functions on topological spaces

See also: Filters in topology § Limits of functions

X, Y가 하우스도르프 공간(Hausdorff space) Y를 갖는 토폴로지적 공간(topological space)으로 가정합니다. p를 Ω ⊆ X, 및 L ∈Y의 극한 점(limit point)으로 놓습니다. 함수 f : Ω → Y에 대해, 그것은 f의 극한은 x가 p에 접근할 때 L이다라고 말하고, 다음과 같이 씁니다:

$\lim _{x\to p}f(x)=L$,

이때 다음 조건이 유지된다는 조건 아래에서 그렇습니다:

L의 모든 각 열린 이웃(neighborhood) V에 대해, f(U ∩ Ω − {p}) ⊆ V를 만족하는 p의 열린 이웃 U가 존재합니다.

그 정의의 마지막 부분은 역시 "f(U∩Ω) ⊆ V를 만족하는 p의 열린 구멍난 이웃(punctured neighbourhood) U가 존재합니다"라고 어구화될 수 있습니다.

f의 도메인은 p를 포함할 필요가 없음에 주목하십시오. 만약 그렇다면, p에서 f의 값은 극한의 정의와 무관합니다. 특히, 만약 f의 도메인이 X − {p} (또는 X의 모두)이면, 만약, 극한 점 p를 갖는 X의 모든 부분-집합 Ω에 대해, Ω에서 f의 제한의 극한이 존재하고 L과 같다면, f의 극한은 x → p일 때 존재하고 L과 같습니다. 때때로 이 기준은 한쪽 극한(one-sided limit)이 존재함에 실패 또는 일치하지 않음을 보여줌으로써 R에 대한 함수의 양-방향 극한의 비-존재를 확립하기 위해 사용됩니다. 그러한 관점은 일반 토폴로지(general topology)의 분야에서 기본이며, 여기서 한 점에서 극한과 연속성은 필터(filters)라고 불리는 부분-집합의 특별한 가족, 또는 넷(nets)으로 알려진 일반화된 수열의 관점에서 정의됩니다.

대안적으로, Y가 하우스도르프 공간이라는 요구-조건은 Y가 일반 토폴로지적 공간이라고 가정하는 것으로 완화될 수 있지만, 그때에 함수의 극한은 고유하지 않을 수 있을 것입니다. 특히, 우리는 한 점에서 함수의 그 극한에 대해 더 이상 이야기할 수 없지만, 오히려 한 점에서 하나의 극한 또는 극한의 집합으로 이야기할 수 있습니다.

함수는 그것의 도메인 안의 및 도메인의 극한 점 p에서 연속인 것과 f(p)가 x가 p로 경향일 때 f(x)의 그 (또는, 일반적인 경우에, 하나의) 극한인 것은 필요충분 조건입니다.

함수의 또 다른 유형의 극한, 즉 수열적 극한(sequential limit)이 있습니다. f : X → Y를 토폴로지적 공간 X에서 하우스도르프 공간 Y로의 매핑이고, p ∈ X를 X의 극한 점이고 L ∈ Y라고 놓습니다. f의 수열적 극한은 x가 p로 가는 경향일 때 다음이면 L입니다:

p에 수렴(converges)하는 X − {p}에서 모든 각 수열(sequence) (x_n)에 대해, 수열 f(x_n)은 L에 수렴(converges)합니다.

만약 L이 x가 p에 접근할 때 f의 위의 의미에서) 극한이면, 그것은 마찬가지로 순열적 극한이고, 어쨌든 그 전환은 일반적으로 유지될 필요가 없습니다. 만약 추가적으로 X가 메트릭-가능(metrizable)이면, L은 x가 p에 접근할 때 f의 순열적 극한인 것과 그것이 x가 p에 접근할 때 f의 (위의 의미에서) 극한인 것은 필요충분 조건입니다.

Other characterizations

In terms of sequences

실수 직선 위에 함수에 대해, 함수의 극한을 정의하는 한 가지 방법은 수열의 극한의 관점입니다. (이 정의는 보통 에두아르트 하이네(Eduard Heine)에 기인합니다.) 이 설정에서:

$\lim _{x\to a}f(x)=L$

인 것과 $a$에 수렴하는 모든 수열 $x_{n}$에 대해 (모든 n에 대해 $x_{n}$이 a와 같지 않은 $x_{n}$과 함께) 수열 $f(x_{n})$이 $L$에 수렴하는 것은 필요충분 조건입니다. 1916년에 이 정의와 위의 정의가 동등하다는 것을 증명되는 것이, 선택의 공리(axiom of choice)의 약한 형식과 동등하고 요구되는 것을 시에르핀스키(Sierpiński)에 의해 보였습니다. 수열 $x_{n}$이 $a$에서 수렴하는 것의 의미를 정의하는 것은 엡실론, 델타 방법(epsilon, delta method)을 필요로 함을 주목하십시오.

비슷하게 그것은 바이어슈트라스의 정의의 경우와 마찬가지로, 보다 일반적인 하이네 정의가 실수 직선의 부분-집합(subsets) 위에 정의된 함수에 적용됩니다. f를 도메인 Dm(f)를 갖는 실수-값 함수로 놓습니다. a를 Dm(f) \ {a}의 원소의 수열의 극한으로 놓습니다. 그런-다음 만약 a로 수렴하는 (모든 n에 대해 $x_{n}$이 a와 같지 않도록) 모든 각 수열 $x_{n}$ ∈ Dm(f) \ {a}에 대해, 수열 $f(x_{n})$이 $L$에 수렴하면, x가 p에 접근할 때 f의 (이 의미에서) 극한은 L입니다. 이것은 유도된 메트릭을 갖는 메트릭 공간일 때 R의 부분-집합 Dm(f)를 고려함으로써 얻어지는 이전 섹션에서 수열적 극한의 정의와 같습니다.

In non-standard calculus

비-표준 미적분학에서, 함수의 극한은 다음에 의해 정의됩니다:

$\lim _{x\to a}f(x)=L$

인 것과 모든 $x\in \mathbb {R} ^{*}$에 대해, $x-a$가 무한소일 때마다 $f^{*}(x)-L$가 무한소인 것은 필요충분 조건입니다. 여기서 $\mathbb {R} ^{*}$는 초실수(hyperreal number)이고 $f^{*}$는 비-표준 실수의 f의 자연스러운 확장입니다. 키슬러(Keisler)는 극한의 그러한 초실수 정의가 두 한정어에 의해 한정어 복잡도를 감소시킨다는 것을 입증했습니다. 다른 한편으로, 흐바섹(Hrbacek)은 모든 초실수에 유효하게 되는 정의에 대해 그들은 암시적으로 ε-δ 방법에 근거되어야 한다라고 쓰고, 교육학적인 관점으로부터, 비-표준 미적분학이 ε-δ 방법 없이 행해질 수 있다는 희망은 절대 완전히 실현될 수 없다고 주장합니다.

Bŀaszczyk et al.은 균등한 연속성의 투명한 정의를 개발하는 것에서 마이크로-연속성(microcontinuity)의 유용성을 상세하게 설명하고, 흐바섹의 비평을 "모호한 애도"로 특징-지었습니다.

In terms of nearness

1908년 국제 수학회에서, 리스 프리제시(Frigyes Riesz)는 "가까움(nearness)"으로 불리는 개념에서 극한과 연속성을 정의하는 대안적인 방법을 소개했습니다. 만약 모든 각 $r>0$에 대해 $|x-a|<r$가 되도록 점 $a\in A$가 있으면, 점 $x$는 집합 $A\subseteq \mathbb {R}$에 가깝게 되는 것이 정의됩니다. 이 설정에서

$\lim _{x\to a}f(x)=L$

인 것과 모든 $A\subseteq \mathbb {R}$에 대해, $a$가 $A$에 가까울 때마다 $L$이 $f(A)$에 가까운 것은 필요충분 조건입니다. 여기서 $f(A)$는 집합 $\{f(x)|x\in A\}$입니다. 이 정의는 역시 메트릭 공간과 토폴로지적 공간으로 확장될 수 있습니다.

Relationship to continuity

Main article: Continuous function

함수의 극한의 개념은 연속성의 개념과 매우 밀접하게 관련됩니다. 만약 c에서 함숫값과 극한 둘 다 정의되고 c에서 그것의 값이 x가 c에 접근할 때 f의 극한과 같으면, 함수 f는 c에서 연속(continuous)이라고 말합니다:

$\lim _{x\to c}f(x)=f(c).$

(우리는 여기서 c는 f의 도메인의 극한 점(limit point)으로 가정해 왔습니다.)

Properties

만약 함수 f가 실수-값이면, p에서 f의 극한이 L인 것과 p에서 f의 오른쪽 극한과 왼쪽 극한이 모두 존재하고 L과 같은 것은 필요충분 조건입니다.

함수 f가 p에서 연속(continuous)인 것과 f(x)의 극한이 x가 p에 접근할 때 존재하고 f(p)와 같은 것은 필요충분 조건입니다. 만약 f : M → N이 메트릭 공간 M과 N 사이의 함수이면, f가 p를 향해 수렴하는 M에서 모든 각 수열을 f(p)를 향해 수렴하는 N에서 수열로 변환하는 것과 동등합니다.

만약 N이 노름 벡터 공간(normed vector space)이면, 극한 연산은 다음 의미에서 선형입니다: 만약 f(x)의 극한이 x가 p에 접근할 때 L이고 g(x)의 극한이 x가 p에 접근할 때 P이면, f(x) + g(x)의 극한은 x가 p에 접근할 때 L + P입니다. 만약 a가 기저 필드(field)의 스칼라이면, af(x)의 극한은 x가 p에 접근할 때 aL입니다.

만약 f와 g가 실수-값 (또는 복소수-값) 함수이면, 특정 조건 아래에서 f(x)와 g(x) 위에 연산 (예를 들어, $f+g$, $f-g$, $f\times g$, $f/g$, $f^{g}$)의 극한을 취하는 것은 f(x)와 g(x)의 극한의 연산과 호환됩니다. 이 사실은 종종 대수적 극한 정리(algebraic limit theorem)라고 불립니다. 다음 규칙을 적용하기 위해 필요한 주요 조건은 방정식의 오른쪽 변에 극한이 존재한다는 것입니다 (다시 말해, 이들 극한은 0을 포함하는 유한한 값입니다). 추가적으로, 나눗셈에 대한 항등식은 오른쪽 변의 분모가 비-영이어야 하고 (0에 의한 나눗셈은 정의되지 않음), 지수에 대한 항등식은 밑이 양수이거나, 지수가 (유한) 양수이면 영임을 요구합니다.

${\begin{matrix}\lim \limits _{x\to p}&(f(x)+g(x))&=&\lim \limits _{x\to p}f(x)+\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)-g(x))&=&\lim \limits _{x\to p}f(x)-\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)\cdot g(x))&=&\lim \limits _{x\to p}f(x)\cdot \lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)/g(x))&=&{\lim \limits _{x\to p}f(x)/\lim \limits _{x\to p}g(x)}\\\lim \limits _{x\to p}&f(x)^{g(x)}&=&{\lim \limits _{x\to p}f(x)^{\lim \limits _{x\to p}g(x)}}\end{matrix}}$

이들 규칙은 p가 ∞ 또는 −∞일 때를 포함하여 한-쪽 극한에도 유효합니다. 위의 각 규칙에서, 오른쪽 극한 중 하나가 ∞ 또는 −∞일 때, 왼쪽 극한은 여전히 다음 규칙에 의해 결정될 수 있습니다.

• q + ∞ = ∞ if q ≠ −∞
• q × ∞ = ∞ if q > 0
• q × ∞ = −∞ if q < 0
• q / ∞ = 0 if q ≠ ∞ and q ≠ −∞
• ∞^q = 0 if q < 0
• ∞^q = ∞ if q > 0
• q^∞ = 0 if 0 < q < 1
• q^∞ = ∞ if q > 1
• q^−∞ = ∞ if 0 < q < 1
• q^−∞ = 0 if q > 1

(확장된 실수 직선(extended real number line)을 참조하십시오).

다른 경우에서, 비록 불확정 형식(indeterminate form)이라고 불리는 오른쪽 변이 결과를 결정할 수 없지만 왼쪽의 극한이 여전히 존재할 수 있습니다. 이것은 함수 f와 g에 따라 다릅니다. 이들 불확정 형식은 다음과 같습니다:

• 0 / 0
• ±∞ / ±∞
• 0 × ±∞
• ∞ + −∞
• 0⁰
• ∞⁰
• 1^±∞

아래 로피탈의 규칙(L'Hôpital's rule)과 불확정 형식(indeterminate form)을 참조하십시오.

Limits of compositions of functions

일반적으로, 다음임을 아는 것에서

$\lim _{y\to b}f(y)=c$ and $\lim _{x\to a}g(x)=b$,

$\lim _{x\to a}f(g(x))=c$를 따르지 않습니다. 어쨌든, 이러한 "체인 규칙"은 다음 추가적인 조건 중 하나가 유지되면 유지됩니다.

• f(b) = c (즉, f는 b에서 연속입니다), 또는
• g는 a 근처에서 값 b를 취하지 않습니다 (즉, 만약 $0<|x-a|<\delta$이면 $|g(x)-b|>0$임을 만족하는 $\delta >0$가 존재합니다).

이 현상의 예제로, 두 추가 제한 사항을 모두 위반하는 다음 함수를 생각해 보십시오:

$f(x)=g(x)={\begin{cases}0&{\text{if }}x\neq 0\\1&{\text{if }}x=0\end{cases}}.$

f(0)에서 값이 제거-가능 불연속(removable discontinuity)이기 때문에,

$\lim _{x\to a}f(x)=0$ for all $a$.

따라서, 소박한 체인 규칙은 f(f(x))의 극한이 0임을 제안할 것입니다. 어쨌든, 다음의 경우에서

$f(f(x))={\begin{cases}1&{\text{if }}x\neq 0\\0&{\text{if }}x=0\end{cases}}$

따라서

$\lim _{x\to a}f(f(x))=1$ for all $a$.

Limits of special interest

Main article: List of limits

Rational functions

$n$ 개의 비-음의 정수와 상수 $a_{1},a_{2},a_{3},\ldots ,a_{n}$와 $b_{1},b_{2},b_{3},\ldots ,b_{n}$에 대해,

• $\lim _{x\to \infty }{\frac {a_{1}{x}^{n}+a_{2}{x}^{n-1}+a_{3}{x}^{n-2}+...+a_{n}}{b_{1}{x}^{n}+b_{2}{x}^{n-1}+b_{3}{x}^{n-2}+...+b_{n}}}={\frac {a_{1}}{b_{1}}}$

이것은 분자와 분모를 모두 $x^{n}$으로 나눔으로써 입증될 수 있습니다. 만약 분자가 더 높은 차수의 다항식이면, 극한이 존재하지 않습니다. 만약 분모가 더 높은 차수이면, 극한은 0입니다.

Trigonometric functions

• $\lim _{x\to 0}{\frac {\sin x}{x}}=1$
• $\lim _{x\to 0}{\frac {1-\cos x}{x}}=0$

Exponential functions

• $\lim _{x\to 0}(1+x)^{\frac {1}{x}}=\lim _{r\to \infty }\left(1+{\frac {1}{r}}\right)^{r}=e$
• $\lim _{x\to 0}{\frac {e^{x}-1}{x}}=1$
• $\lim _{x\to 0}{\frac {e^{ax}-1}{bx}}={\frac {a}{b}}$
• $\lim _{x\to 0}{\frac {c^{ax}-1}{bx}}={\frac {a}{b}}\ln c$
• $\lim _{x\to 0^{+}}x^{x}=1$

Logarithmic functions

• $\lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1$
• $\lim _{x\to 0}{\frac {\ln(1+ax)}{bx}}={\frac {a}{b}}$
• $\lim _{x\to 0}{\frac {\log _{c}(1+ax)}{bx}}={\frac {a}{b\ln c}}$

L'Hôpital's rule

Main article: l'Hôpital's rule

이 규칙은 불확정 형식(indeterminate forms) 0/0 또는 ±∞/∞의 극한을 찾기 위해 도함수(derivatives)를 사용하고, 그러한 경우에만 적용됩니다. 다른 불확정 형식은 이 형식으로 조작될 수 있습니다. 원하는 극한 점 c를 포함하는 열린 구간(open interval) I에 걸쳐 정의된 두 함수 f(x)와 g(x)가 주어질 때, 만약 다음이면:

1. $\lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0,$ or $\lim _{x\to c}f(x)=\pm \lim _{x\to c}g(x)=\pm \infty$, 그리고
2. $f$와 $g$가 $I\setminus \{c\}$에 걸쳐 미분-가능입니다, 그리고
3. 모든 $x\in I\setminus \{c\}$에 대해 $g'(x)\neq 0$, 그리고
4. $\lim _{x\to c}{\frac {f'(x)}{g'(x)}}$가 존재합니다,

다음입니다:

$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}$.

통상적으로, 첫 번째 조건은 가장 중요한 것입니다.

예를 들어: $\lim _{x\to 0}{\frac {\sin(2x)}{\sin(3x)}}=\lim _{x\to 0}{\frac {2\cos(2x)}{3\cos(3x)}}={\frac {2\cdot 1}{3\cdot 1}}={\frac {2}{3}}.$

Summations and integrals

합계 또는 적분에 무한 경계를 지정하는 것은 극한을 지정하기 위한 공통적인 속기입니다.

극한 $\lim _{n\to \infty }\sum _{i=s}^{n}f(i)$을 쓰기 위한 짧은 방법은 $\sum _{i=s}^{\infty }f(i)$입니다. 이것들과 같은 합의 극한의 중요한 예시는 급수(series)입니다.

극한 $\lim _{x\to \infty }\int _{a}^{x}f(t)\;dt$을 쓰기 위한 짧은 방법은 $\int _{a}^{\infty }f(t)\;dt$입니다.

극한 $\lim _{x\to -\infty }\int _{x}^{b}f(t)\;dt$을 쓰기 위한 짧은 방법은 $\int _{-\infty }^{b}f(t)\;dt$입니다.

See also

• Big O notation
• L'Hôpital's rule
• List of limits
• Limit of a sequence
• Limit superior and limit inferior
• Net (mathematics)
• Non-standard calculus
• Squeeze theorem
• Subsequential limit

References

• Apostol, Tom M. (1974), Mathematical Analysis (2 ed.), Addison–Wesley, ISBN 0-201-00288-4
• Bartle, Robert (1967), The elements of real analysis, Wiley
• Courant, Richard (1924), Vorlesungen über Differential- und Integralrechnung, Springer Verlag
• Hardy, G.H. (1921), A course in pure mathematics, Cambridge University Press
• Hubbard, John H. (2015), Vector calculus, linear algebra, and differential forms: A unified approach (Fifth ed.), Matrix Editions
• Page, Warren; Hersh, Reuben; Selden, Annie; et al., eds. (2002), "Media Highlights", The College Mathematics, 33 (2): 147–154, JSTOR 2687124.
• Rudin, Walter (1964), Principles of mathematical analysis, McGraw-Hill
• Sutherland, W. A. (1975), Introduction to Metric and Topological Spaces, Oxford: Oxford University Press, ISBN 0-19-853161-3
• Sherbert, Robert (2000), Introduction to real analysis, Wiley
• Whittaker; Watson (1904), A Course of Modern Analysis, Cambridge University Press

External links

• MacTutor History of Weierstrass.
• MacTutor History of Bolzano
• Visual Calculus by Lawrence S. Husch, University of Tennessee (2001)