Factorial

Original article: w:Factorial

This article is about products of consecutive integers. For statistical experiments over all combinations of values, see factorial experiment. For data representation by independent components, see factorial code.

Selected factorials; values in scientific notation are rounded

$n$	$n!$
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	1.551121004×1025
50	3.041409320×1064
70	1.197857167×10100
100	9.332621544×10157
450	1.733368733×101000
1000	4.023872601×102567
3249	6.412337688×1010000
10000	2.846259681×1035659
25206	1.205703438×10100000
100000	2.824229408×10456573
205023	2.503898932×101000004
1000000	8.263931688×105565708
10100	1010101.9981097754820

수학(mathematics)에서, 비-음의 정수(integer) $n$의 팩토리얼(factorial)은, $n!$에 의해 표시되며, $n$보다 작거나 같은 모든 양의 정수의 곱(product)입니다. $n$의 팩토리얼은 역시 다음 더 작은 팩토리얼과 $n$의 곱과 같습니다: $${\begin{aligned}n!&=n\times (n-1)\times (n-2)\times (n-3)\times \cdots \times 3\times 2\times 1\\&=n\times (n-1)!\\\end{aligned}}$$ 예를 들어, $$5!=5\times 4\times 3\times 2\times 1=5\times 24=120.$$

0!의 값은 빈 곱(empty product)에 대해 관례에 따라 1입니다.

팩토리얼은 여러 고대 문화, 특히 자이나교 문학(Jain literature)의 정식의 작품에서 인도 수학(Indian mathematics)에서, 및 탈무드 책 Sefer Yetzirah에서 유대 신비주의자에 의해 발견되어 왔습니다. 팩토리얼 연산은 수학의 많은 영역, 특히 조합론(combinatorics)에서 만나게 되며, 여기서 가장 기본적인 사용은 $n$ 구별되는 대상의 가능한 구별되는 수열(sequence) – 순열(permutation) – 을 세는 것입니다: $n!$이 있습니다. 수학적 해석학(mathematical analysis)에서, 팩토리얼은 지수 함수(exponential function)와 다른 함수에 대해 거듭제곱 급수(power series)에 사용되고, 그것들은 역시 대수학(algebra), 숫자 이론(number theory), 확률 이론(probability theory), 및 컴퓨터 과학(computer science)에 응용을 가집니다.

팩토리얼 함수의 수학의 대부분은 18세기 후반과 19세기 초반에 개발되었습니다. 스털링의 근사(Stirling's approximation)는 큰 숫자의 팩토리얼에 대한 정확한 근사를 제공하여, 그것이 지수 성장(exponential growth)보다 더 빠르게 성장함을 보여줍니다. 르장드르의 공식(Legendre's formula)은 팩토리얼의 소수 인수분해(prime factorization)에서 소수의 지수를 설명하고, 팩토리얼의 후행하는 영들을 세기 위해 사용될 수 있습니다. 다니엘 베르누이(Daniel Bernoulli)와 레온하르트 오일러(Leonhard Euler)는 음의 정수에서, (오프셋) 감마 함수(gamma function)를 제외하고 팩토리얼 함수를 복소수(complex number)의 연속 함수로 보간(interpolate)했습니다.

다른 많은 주목할만한 함수와 숫자 수열은 이항 계수(binomial coefficient), 두-배 팩토리얼(double factorial), 떨어지는 팩토리얼(falling factorial), 프리모리얼(primorial), 및 부분팩토리얼(subfactorial)을 포함하여 팩토리얼과 밀접하게 관련되어 있습니다. 팩토리얼 함수의 구현은 공통적으로 다양한 컴퓨터 프로그래밍(computer programming) 스타일의 예제로 사용되고, 과학 계산기(scientific calculator)와 과학 컴퓨팅 소프트웨어 라이브러리에 포함됩니다. 비록 곱 공식이나 재귀를 사용하여 큰 팩토리얼을 직접 계산하는 것은 효율적이지 않지만, 더 빠른 알고리듬은 같은 자릿수의 숫자를 갖는 숫자에 대해 빠른 곱셈 알고리듬(multiplication algorithm)에 대해 상수 인수 내에서 시간을 일치시키는 것이 알려져 있습니다.

History

팩토리얼의 개념은 많은 문화권에서 독립적으로 발생해 왔습니다:

• 인도 수학(Indian mathematics)에서, 팩토리얼의 가장 오래된 알려진 설명 중 하나는 Anuyogadvāra-sūtra, 자이나교 문학(Jain literature)의 정식의 작품 중 하나에서 오며, 이것은 기원전 300년에서 기원후 400년까지 변하는 날짜를 할당해 왔습니다. 그것은 항목의 집합의 정렬과 역순을 다른 ("혼합된") 순서와 분리하여, 팩토리얼에 대해 보통의 곱 공식에서 2를 뺌으로써 혼합된 순서의 숫자를 평가합니다. 순열에 대해 곱 규칙은 6세기 CE 자이나교 수도사 Jinabhadra에 의해 설명되었습니다. 힌두 학자들은 적어도 1150년부터 팩토리얼 공식을 사용해 왔으며, 바스카라 2세(Bhāskara II)는 그의 저서 릴라바티(Līlāvatī)에서, 비슈누(Vishnu)가 그의 4가지 특징적인 대상 (소라 껍질, 원반, 철퇴, 및 연꽃)을 그의 네 손에 얼마나 많이 잡을 수 있었는지 문제와 열-손 신에 대해 문제 유사한 문제와 관련하여 팩토리얼을 언급했습니다.
• 중동의 수학에서, 탈무드 시대(Talmudic period) (기원후 200–500년)에서 히브리 신비주의 창조서 Sefer Yetzirah는 계승을 7!까지 히브리어 알파벳(Hebrew alphabet)에서 형성될 수 있는 단어의 숫자에 대한 조사의 일환으로 나열합니다. 팩토리얼은 8세기 아랍 문법학자 Al-Khalil ibn Ahmad al-Farahidi도 비슷한 이유로 연구했습니다. 아랍 수학자 이븐 알-하이삼(Ibn al-Haytham) (역시 알하젠(Alhazen)으로 알려져 있음, c. 965 – c. 1040)은 팩토리얼과 소수(prime number)를 연결하는 윌슨의 정리(Wilson's theorem)를 최초로 공식화했습니다.
• 유럽에서, 비록 그리스 수학(Greek mathematics)은 일부 조합론을 포함하고 있고, 플라톤(Plato)은 부분적으로 그것의 나눔가능성 속성 때문에 이상적인 공동체의 모집단으로 5040 (팩토리얼)을 유명하게 사용했지만, 고대 그리스에서 팩토리얼의 연구의 직접적인 증거는 없습니다. 대신, 유럽에서 팩토리얼에 대한 첫 번째 연구는 샤베타이 돈놀로(Shabbethai Donnolo)와 같은 유대인 학자에 의한 것이며, Sefer Yetzirah 구절을 설명했습니다. 1677년에, 영국 작가 파비안 스테드먼(Fabian Stedman)은 여러 개의 조율된 종이 울리는 것을 포함하는 음악 예술, 링잉을 변경하기 위한 팩토리얼의 응용을 설명했습니다.

15세기 후반부터, 팩토리얼은 서양 수학자들의 연구 주제가 되었습니다. 1494년 논문에서, 이탈리아 수학자 루카 파치올리(Luca Pacioli)는 식탁 배열 문제와 관련하여 최대 11!까지 팩토리얼을 계산했습니다. 크리스토퍼 클라비우스(Christopher Clavius)는 사크로보스코의 요한네스(Johannes de Sacrobosco)의 연구에 대한 1603년 논평에서 팩토리얼을 논의했고, 1640년대에, 프랑스의 폴리매쓰 마랭 메르센(Marin Mersenne)은 클라비우스의 연구를 기반으로 64!까지 팩토리얼의 큰 테이블을 출판했습니다 (그러나 완전히 정확하지는 않습니다). 지수 함수(exponential function)에 대해 거듭제곱 급수(power series)는, 그것의 계수에 대해 팩토리얼의 역수와 함께, 1676년 아이작 뉴턴(Isaac Newton)에 의한 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)에게 보낸 편지에서 처음 공식화되었습니다. 팩토리얼에 대한 초기 유럽 수학의 다른 중요한 연구는 1685년 존 월리스(John Wallis)에 의한 논문, 1721년 아브라암 드 무아브르(Abraham de Moivre)에 의한 $n$의 큰 값에 대해 근삿값 연구, 제임스 스털링(James Stirling)에서 스털링의 근사(Stirling's approximation)로 알려지게 되는 것을 말하는 드 무아브르에게 보내는 1729년 편지, 및 같은 시기에 감마 함수(gamma function)에 대한 팩토리얼 함수의 연속 확장을 공식화한 다니엘 베르누이(Daniel Bernoulli)와 레온하르트 오일러(Leonhard Euler)에 의한 연구에서 광범위하게 다루어졌습니다. 아드리앵-마리 르장드르(Adrien-Marie Legendre)는 1808년 숫자 이론(number theory)에 관한 텍스트에서 팩토리얼을 소수 거듭제곱(prime power)으로 인수분해(factorization)에서 지수를 설명하는 르장드르의 공식(Legendre's formula)을 포함했습니다.

팩토리얼에 대해 표기법 $n!$은 1808년 프랑스 수학자 크리스티앙 크랑(Christian Kramp)에 의해 도입되었습니다. 많은 다른 표기법이 역시 사용되어 왔습니다. 팩토리얼의 인수가 상자의 왼쪽과 아래쪽 변으로 반쯤 둘러싸이는 또 다른 후기 표기법은 영국과 미국에서 한동안 인기가 있었지만 조판하기가 어렵기 때문에 사용되지 않게 되었습니다. 단어 "factorial" (원래 프랑스어: factorielle)는 1800년에 루이 프랑수아 앙투안 아르보가(Louis François Antoine Arbogast)에 의해 파 디 브루노의 공식(Faà di Bruno's formula)에 대한 첫 번째 연구에서 처음 사용되었지만, 산술 진행(arithmetic progression)의 곱의 보다 일반적인 개념을 참조합니다. 이 이름이 참조하는 "인수"는 팩토리얼에 대해 곱 공식의 용어입니다.

Definition

양의 정수 $n$의 팩토리얼 함수는 다음 곱에 의해 정의됩니다: $$n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n.$$

이것은 다음처럼 곱 표기법(product notation)에서 보다 간결하게 쓸 수 있습니다: $$n!=\prod _{i=1}^{n}i.$$

만약 이 곱 공식이 마지막 항을 제외한 모든 항을 유지하도록 변경되면, 그것은 더 작은 팩토리얼에 대해 같은 형식의 곱을 정의할 것입니다. 이것은 재귀 관계(recurrence relation)로 이어지며, 이에 따라 팩토리얼 함수의 각 값은 이전 값에 $n$을 곱함으로써 얻어질 수 있습니다: $$n!=n\cdot (n-1)!.$$

예를 들어, $5!=5\cdot 4!=5\cdot 24=120$.

Factorial of zero

$0$의 팩토리얼은 $1$이며, 기호에서, $0!=1$입니다. 이 표기법에 대해 여러 동기가 있습니다:

• $n=0$에 대해, 곱으로 $n!$의 정의는 전혀 숫자없는 곱과 관련되고, 인수가 없는 곱, 빈 곱(empty product)이 곱셈 항등원과 같다는 더 넓은 관례의 예제이기도 합니다.
• 영 대상의 정확하게 하나의 순열이 있습니다: 순열하려는 것이 없으면, 유일한 재배열은 아무것도 하지 않는 것입니다.
• 이 관례는 조합론(combinatorics)에서 많은 항등식을 그것들의 매개변수의 모든 유효한 선택에 대해 유효하게 만듭니다. 예를 들어, $n$ 집합에서 모든 $n$ 원소를 선택하는 방법의 숫자는 ${\textstyle {\tbinom {n}{n}}={\tfrac {n!}{n!0!}}=1}$이며, $0!=1$일 때만 유효한 이항 계수(binomial coefficient) 항등식입니다.
• $0!=1$과 함께, 팩토리얼에 대해 재귀 관계는 $n=1$에서 유효하게 남습니다. 그러므로, 이 관례와 함께, 팩토리얼의 재귀(recursive) 계산은 기본 경우(base case)로 영에 대해 값만 가질 필요가 있으며, 계산을 단순화하고 추가적인 특수 경우에 대한 필요성을 피합니다.
• $0!=1$를 설정하는 것은 지수 함수(exponential function)를 거듭제곱 급수(power series)와 같은 많은 공식의 간결한 표현을 허용합니다: ${\textstyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.}$
• 이 선택은 감마 함수(gamma function) $0!=\Gamma (0+1)=1$를 조화롭게 하고, 감마 함수는 이 값을 연속 함수(continuous function)로 가져야 합니다.

Applications

팩토리얼 함수의 가장 최초의 사용은 순열(permutations)을 세는 것을 포함합니다: $n$ 구별되는 대상을 수열로 배열하는 $n!$ 다른 방법이 있습니다. 팩토리얼은 대상의 다른 순서화를 설명하기 위해 조합론(combinatorics)에서 많은 공식에 더 광범위하게 나타납니다. 예를 들어, 이항 계수(binomial coefficient) ${\tbinom {n}{k}}$는 $n$ 원소를 갖는 집합에서 $k$-원소 조합(combination) ($k$-원소의 부분집합)을 세고, 다음 공식을 사용하여 팩토리얼에서 계산될 수 있습니다: $${\binom {n}{k}}={\frac {n!}{k!(n-k)!}}.$$ 첫 번째 종류의 스털링 숫자(Stirling numbers of the first kind)는 팩토리얼을 합하고, $n$의 순열을 같은 주기의 숫자를 갖는 부분집합으로 그룹화하여 셉니다. 또 다른 조합론적 응용은 그것의 원래 위치에 임의의 원소를 남겨두지 않는 순열, 교란(derangement)을 세는 것입니다; $n$ 항목의 교란의 숫자는 $n!/e$에 가장 가까운 정수(nearest integer)입니다.

대수학(algebra)에서, 팩토리얼은 이항 계수를 합의 거듭제곱을 확장하기 위해 사용하는 이항 정리(binomial theorem)를 통해 발생합니다. 그것들은 역시 예를 들어 대칭 다항식(symmetric polynomial)에 대해 뉴턴의 항등식(Newton's identities)에서 특정 다항식의 가족을 서로 관련시키기 위해 사용되는 계수에서 발생합니다. 순열을 세는 것에서 그것들의 사용은 역시 대수학적으로 다시 설명할 수 있습니다: 팩토리얼은 유한 대칭 그룹(symmetric group)의 차수(orders)입니다. 미적분학(calculus)에서, 팩토리얼은 더 높은 도함수를 연결하기 위해 파 디 브루노의 공식(Faà di Bruno's formula)에서 발생합니다. 수학적 해석학(mathematical analysis)에서, 팩토리얼은 거듭제곱 급수(power series), 특히 지수 함수(exponential function)에 대해 급수에서 분모에 자주 나타납니다: $$e^{x}=1+{\frac {x}{1}}+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots =\sum _{i=0}^{\infty }{\frac {x^{i}}{i!}},$$ 그리고 다른 테일러 급수(Taylor series) (특히 삼각(trigonometric)과 쌍곡 함수의 그것)의 계수에서 나타나며, 여기서 그것들은 $x^{n}$의 $n$-번째 도함수에서 오는 $n!$의 인수를 취소합니다. 거듭제곱 급수에서 팩토리얼의 이 사용법은 크기 $i$의 $n_{i}$ 원소를 갖는 조합론적 클래스(combinatorial class)에 대해 다음 거듭제곱 급수로 정의되는 지수 생성하는 함수(exponential generating function)를 통해 해석적 조합론(analytic combinatorics)을 다시 연결합니다: $$\sum _{i=0}^{\infty }{\frac {x^{i}n_{i}}{i!}}.$$

숫자 이론(number theory)에서, 팩토리얼의 가장 두드러진 속성은 르장드르의 공식(Legendre's formula)에 의한 소수 인수에 대해 더 정확하게 설명되는 $n!$을 $n$까지 모든 양의 정수에 의한 나눔가능성(divisibility)입니다. 그것은 임의적으로 큰 소수(prime number)가 숫자 $n!\pm 1$의 소수 인수로 구할 수 있음을 따르며, 소수의 숫자가 무한하다는 유클리드의 정리(Euclid's theorem)의 증명으로 이어집니다. $n!\pm 1$가 자체로 소수일 때, 그것은 팩토리얼 소수(factorial prime)라고 불립니다; 관련하여, 브로카르의 문제(Brocard's problem)는, 역시 스리미바자 라마누젠(Srinivasa Ramanujan)에 의해 제기되었으며, 형식 $n!+1$의 제곱 숫자(square number)의 존재와 관계합니다. 대조적으로, 숫자 $n!+2,n!+3,\dots n!+n$는 모두 합성수여야 하며, 임의적으로 큰 소수 틈(prime gap)의 존재를 제공합니다. 형식 $[n,2n]$의 임의의 구간에서 소수의 존재에 대한 기본 베르트랑 추측의 증명(proof of Bertrand's postulate)은, 폴 에르되시(Paul Erdős)의 첫 번째 결과 중 하나이며, 팩토리얼의 나눔가능성 속성을 기반으로 했습니다. 팩토리얼 숫자 시스템(factorial number system)은 숫자에 대해 혼합된 기수(mixed radix) 표기법이며, 이것에서 각 자릿수의 위치 값은 팩토리얼입니다.

팩토리얼은 확률 이론(probability theory), 예를 들어 푸아송 분포(Poisson distribution)와 무작위 순열(random permutation)의 확률에서 광범위하게 사용됩니다. 컴퓨터 과학(computer science)에서, 순열에 걸쳐 무차별-강제 검색(brute-force search)의 분석에 나타나는 것 외에도, 팩토리얼은 $n$ 항목의 집합을 비교 정렬(comparison sort)에 필요된 비교의 숫자에 대한 $\log _{2}n!=n\log _{2}n-O(n)$의 아래쪽 경계(lower bound)에서 발생하고, 셀당 키의 분포가 푸아송 분포에 의해 정확하게 근사화되는 연쇄된 해시 테이블(hash table)의 분석에서 나타납니다. 게다가, 팩토리얼은 종종 입자의 집합의 모든 가능한 순열을 고려하는 양자(quantum)와 통계적 물리학(statistical physics)에서 공식에 자연스럽게 나타납니다. 통계적 역학(statistical mechanics)에서, 볼츠만의 엔트로피 공식(Boltzmann's entropy formula) 또는 자쿠어–테트로더 방정식(Sackur–Tetrode equation)과 같은 엔트로피(entropy)의 계산은 깁스 역설(Gibbs paradox)을 피하기 위해 각 유형의 구별할-수-없는 입자(indistinguishable particle)의 숫자의 팩토리얼로 나눔으로써 미시상태(microstates)의 카운트를 수정해야 합니다. 양자 물리학은 이들 수정이 필요한 근본적인 이유를 제공합니다.

Properties

Growth and approximation

Comparison of the factorial, Stirling's approximation, and the simpler approximation $(n/e)^{n}$, on a doubly logarithmic scale

Relative error in a truncated Stirling series vs. number of terms

Main article: Stirling's approximation

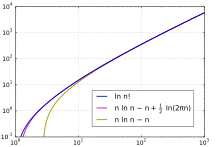
$n$의 함수로서, 팩토리얼은 지수 성장(exponential growth)보다 더 빠르지만, 이중 지수 함수(double exponential function)보다 느리게 성장합니다. 그것의 성장률은 $n^{n}$과 유사하지만, 지수 인수만큼 더 느립니다. 이 결과에 접근하는 한 가지 방법은 팩토리얼의 자연 로그(natural logarithm)를 취하여, 그것의 곱 공식을 합으로 바꾸고, 그런-다음 적분으로 합을 추정하는 것입니다: $$\ln n!=\sum _{x=1}^{n}\ln x\approx \int _{1}^{n}\ln x\,dx=n\ln n-n+1.$$

결과를 지수화 (및 무시할 수 있는 $+1$을 무시)하면 $n!$을 $(n/e)^{n}$으로 근사화합니다. 사다리꼴 규칙(trapezoid rule)을 사용하여 적분으로 위와 아래의 합을 더 신중하게 경계하면, 이 추정값이 ${\sqrt {n}}$에 비례하는 수정 항이 필요하다는 것을 보여줍니다. 이 수정에 대해 비례성의 상수는 $\pi$를 팩토리얼과 이의 거듭제곱의 극한하는 비율로 나타내는 월러스 곱(Wallis product)에서 구할 수 있습니다. 이들 수정의 결과는 스털링의 근사(Stirling's approximation)입니다: $$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\,.$$

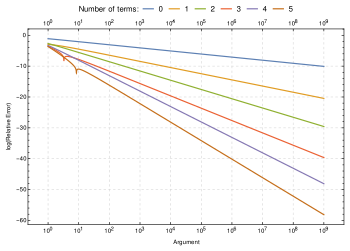
여기서, $\sim$ 기호는, $n$이 무한대로 접근할 때, 왼쪽과 오른쪽 변 사이의 비율이 극한(limit)에서 일로 접근한다는 것을 의미합니다. 스털링의 공식은 더 많은 숫자의 항을 취했을 때 훨씬 더 정확하게 되는 점근적 급수(asymptotic series)에서 첫 번째 항을 제공합니다: $$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots \right).$$

대안적인 버전은 수정 항에서 오직 홀수 지수를 사용합니다: $$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \left({\frac {1}{12n}}-{\frac {1}{360n^{3}}}+{\frac {1}{1260n^{5}}}-{\frac {1}{1680n^{7}}}+\cdots \right).$$

이들 공식의 많은 다른 변형은 역시 스리미바자 라마누젠(Srinivasa Ramanujan), 빌 가스퍼(Bill Gosper), 및 다른 사람들에 의해 개발되어 왔습니다.

비교 정렬(comparison sort)을 분석하기 위해 사용되는 팩토리얼의 이진 로그(binary logarithm)는 스털링의 근사를 사용하여 매우 정확하게 추정될 수 있습니다. 아래 공식에서, $O(1)$ 항은 큰 O 표기법(big O notation)을 호출합니다: $$\log _{2}n!=n\log _{2}n-(\log _{2}e)n+{\frac {1}{2}}\log _{2}n+O(1).$$

Divisibility and digits

Main article: Legendre's formula

팩토리얼에 대해 곱 공식은 $n!$이 많아야 $n$인 모든 소수(prime number)로 나뉠(divisible) 수 있고, 더 큰 소수로는 나뉠 수 없음을 의미합니다. 그것의 나눔가능성에 대한 보다 정확한 정보는 르장드르의 공식(Legendre's formula)에 의해 제공되며, 이것은 $n!$의 소수 인수분해에서 각 소수 $p$의 지수를 제공합니다: $$\sum _{i=1}^{\infty }\left\lfloor {\frac {n}{p^{i}}}\right\rfloor ={\frac {n-s_{p}(n)}{p-1}}.$$

여기서 $s_{p}(n)$는 $n$의 밑수(base)-$p$ 자릿수의 합을 나타내고, 이 공식에 의해 주어진 지수는 역시 고급 수학에서 팩토리얼의 p진수 평가(p-adic valuation)로 해석될 수 있습니다. 르장드르의 공식을 이항 계수(binomial coefficient)에 대해 곱 공식에 적용하면 쿠머의 공식(Kummer's theorem), 이항 계수의 인수분해에서 각 소수의 지수에 대한 유사한 결과를 생성합니다.

$p=5$에 대해 르장드르 공식의 특별한 경우는 팩토리얼의 십진 표시에서 후행하는 영들(trailing zeros)의 숫자를 제공합니다. 이 공식에 따르면, 영들의 숫자는 $n$에서 $n$의 밑수-5 자리를 빼고, 그 결과를 사로 나눔으로써 얻어질 수 있습니다. 르장드르 공식은 소수 $p=2$의 지수가 항상 $p=5$에 대해 지수보다 크므로, 오의 각 인수는 이들 후행하는 영 중 하나를 생성하기 위해 이의 인수와 쌍을 이룰 수 있습니다. 팩토리얼의 선행하는 자릿수는 벤포드의 법칙(Benford's law)에 따라 분포됩니다. 임의의 밑수에서, 모든 각 자릿수의 수열은 해당 밑수에서 일부 팩토리얼 숫자의 초기 자릿수의 수열입니다.

팩토리얼의 나눔가능성에 대한 또 다른 결과, 윌슨의 정리(Wilson's theorem)는 $(n-1)!+1$은 $n$으로 나뉠 수 있는 것과 $n$이 소수(prime number)인 것은 필요충분 조건이라고 말합니다. 임의의 주어진 정수 $x$에 대해, $x$의 캠프너 함수는 $x$가 $n!$을 나누는 가장 작은 $n$에 의해 제공됩니다. 거의 모든 숫자 (점근적 밀도(asymptotic density) 영을 갖는 예외의 부분집합을 제외하고 모두)에 대해, 그것은 $x$의 가장 큰 소수 인수와 일치합니다.

두 팩토리얼의 곱, $m!\cdot n!$은 항상 $(m+n)!$를 균등하게 나눕니다. 다른 팩토리얼의 곱과 같은 무한하게 많은 팩토리얼이 있습니다: 만약 $n$이 자체로 임의의 팩토리얼의 곱이면, $n!$은 같은 곱에 하나 더 팩토리얼, $(n-1)!$을 곱한 것과 같습니다. 다른 팩토리얼의 곱이지만 이 "자명한" 형식이 아닌 팩토리얼의 유일한 알려진 예제는 $9!=7!\cdot 3!\cdot 3!\cdot 2!$, $10!=7!\cdot 6!=7!\cdot 5!\cdot 3!$, 및 $16!=14!\cdot 5!\cdot 2!$입니다. 그것은 단지 유한하게 많은 비-자명한 예제가 있다는 abc 추측(abc conjecture)에서 따를 것입니다.

정수에 걸쳐 차수 $d$의 원시 다항식(primitive polynomial)의 값의 최대 공통 약수(greatest common divisor)는 $d!$를 균등하게 나눕니다.

Continuous interpolation and non-integer generalization

The gamma function (shifted one unit left to match the factorials) continuously interpolates the factorial to non-integer values

Absolute values of the complex gamma function, showing poles at non-positive integers

Main article: Gamma function

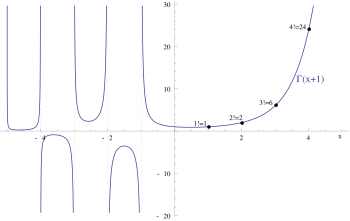
팩토리얼을 연속 함수(continuous function)로 확장하는 무한하게 많은 방법이 있습니다. 이들 중 가장 널리 사용된 것은 양의 실수에 대해 다음 적분(integral)으로 정의될 수 있는 감마 함수(gamma function)를 사용합니다: $$\Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx.$$

결과 함수는 다음 방정식에 의해 비-음의 정수 $n$의 팩토리얼과 관련됩니다: $$n!=\Gamma (n+1),$$

이것은 비-정수 인수에 대해 팩토리얼의 정의로 사용될 수 있습니다. $\Gamma (x)$와 $\Gamma (x-1)$ 둘 다가 정의되는 모든 값 $x$에서, 감마 함수는 다음 함수형 방정식(functional equation)을 따릅니다: $$\Gamma (n)=(n-1)\Gamma (n-1),$$

이것은 팩토리얼에 대해 재귀 관계(recurrence relation)를 일반화합니다.

같은 적분은 그것의 실수 부분이 양수인 임의의 복소수(complex number) $z$에 대해 더 일반적으로 수렴합니다. 그것은 다음 오일러의 반사 공식(reflection formula)에 대해 풂으로써 복소 평면(complex plane)의 나머지 부분에서 비-정수 점으로 확장될 수 있습니다. $$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}.$$

어쨌든, 이 공식은 정수에서 사용될 수 없는데, 왜냐하면, 그것들에 대해, $\sin \pi z$ 항은 영에 의한 나눗셈(division by zero)을 생성할 것이기 때문입니다. 이 확장 과정의 결과는 해석적 함수(analytic function), 감마 함수에 대해 적분 공식의 해석적 연속화(analytic continuation)입니다. 그것은 단순 극(simple poles)을 가지는 비-양의 정수를 제외하고 모든 복소수에서 비-영 값을 가집니다. 이에 따라, 이것은 음의 정수 이외의 모든 복소수에서 팩토리얼에 대해 하나의 정의를 제공합니다. 팩토리얼의 다른 연속 보간과 구별하는 감마 함수의 한 속성은 보어–몰러럽 정리(Bohr–Mollerup theorem)에 의해 제공되며, 그 정리는 감마 함수 (1만큼 오프셋됨)가 팩토리얼을 보간하고 같은 함수형 방정식을 따르는 양의 실수에 대한 유일한 로그-볼록(log-convex) 함수임을 말합니다. 헬무트 빌런트(Helmut Wielandt)의 관련된 고유성 정리는 복소수 감마 함수와 그것의 스칼라 배수는 양의 복소수 반-평면에서 함수형 방정식을 따르고 1과 2 사이의 실수 부분을 갖는 복소수에 대해 경계지게 남는 유일한 정칙 함수(holomorphic function)임을 말합니다.

팩토리얼 값을 보간하는 다른 복소수 함수는 비-양의 정수를 포함하는 모든 복소수에 걸쳐 전체 함수(entire function)인 아다마르의 감마 함수(Hadamard's gamma function)를 포함합니다. p-진수 숫자(p-adic number)에서, 큰 정수의 팩토리얼 (p-진수의 조밀한 부분집합)이 르장드르의 공식에 따라 영으로 수렴하고, 그것들에 가까운 임의의 연속 함수를 모든 곳에서 영이 되도록 강제하기 때문에 팩토리얼 함수를 직접 연속적으로 보간하는 것은 불가능합니다. 대신, p-진수 감마 함수(p-adic gamma function)는 팩토리얼의 수정된 형식을 연속 보간을 제공하여, p로 나뉠 수 있는 팩토리얼의 인수를 생략합니다.

디감마 함수(digamma function)는 감마 함수의 로그 도함수(logarithmic derivative)입니다. 감마 함수가 일만큼 오프셋된 팩토리얼의 연속적인 보간을 제공하는 것처럼, 디감마 함수는 오일러–마스케로니 상수(Euler–Mascheroni constant)에 의해 오프셋된 조화 숫자(harmonic number)의 연속적인 보간을 제공합니다.

Computation

TI SR-50A, a 1975 calculator with a factorial key (third row, center right)

팩토리얼 함수는 과학적 계산기(scientific calculator)의 공통적인 특색입니다. 그것은 역시 파이선 수학적 함수 모듈과 부스트 C++ 라이브러리와 같은 과학적 프로그래밍 라이브러리에 포함되어 있습니다. 만약 효율성이 중요하지 않다면, 팩토리얼을 계산하는 것은 자명합니다: 단지 $1$로 초기화된 변수에 $n$까지의 정수를 연속적으로 곱하면 됩니다. 이 계산의 단순성은 다양한 컴퓨터 프로그래밍 스타일과 방법의 사용에서 그것을 공통적인 예제로 만듭니다. $n!$의 계산은 반복(iteration)을 사용하여 유사코드(pseudocode)에서 다음과 같이 표현될 수 있습니다:

define factorial(n):

f := 1

for i := 1, 2, 3, ... n:

f := f × i

return f

또는 다음과 같은 재귀 관계를 기반으로 재귀(recursion)를 사용하여:

define factorial(n):

if n = 0 return 1

return n × factorial(n − 1)

계산에 적합한 다른 방법은 메모이제이션(memoization), 동적 프로그래밍(dynamic programming), 및 함수형 프로그래밍(functional programming)을 포함합니다. 이들 알고리듬의 계산 복잡성(computational complexity)은 각 산술 연산이 일정한 시간을 취하고 각 숫자가 일정한 총양의 저장 공간을 사용하는 계산의 단위-비용 무작위-접근 기계(random-access machine) 모델을 사용하여 분석될 수 있습니다. 이 모델에서, 이들 방법은 $n!$을 시간 $O(n)$에서 계산될 수 있고, 반복 버전은 공간 $O(1)$을 사용합니다. 꼬리 재귀(tail recursion)에 최적화되지 않은 한, 재귀 버전은 그것의 호출 스택(call stack)을 저장하기 위해 선형 공간을 차지합니다. 어쨌든, 이 계산의 모델은 $n$이 $n!$을 기계어(machine word)에 맞추기 위해 허용할 만큼 충분히 작을 때 오직 적합합니다. 값 12!와 20!은 각각 32-비트와 64-비트 정수에 저장될 수 있는 가장 큰 팩토리얼입니다. 부동 점은 더 큰 팩토리얼을 나타낼 수 있지만, 정확하기 보다는 근사적이고, $170!$보다 큰 팩토리얼에 대해 여전히 오버플로될 것입니다.

더 큰 팩토리얼의 정확한 계산은 임의적인-정밀도 산술(arbitrary-precision arithmetic)을 포함하고, 그것의 시간은 결과에서 자릿수 또는 비트의 숫자의 함수로 분석될 수 있습니다. 스털링의 공식에 의해, $n!$은 $b=O(n\log n)$ 비트를 가집니다. 쇤하게–슈트라센 알고리듬(Schönhage–Strassen algorithm)은 $b$-비트 곱을 시간 $O(b\log b\log \log b)$에서 생성할 수 있고, 시간 $O(b\log b)$을 취하는 더 빠른 곱셈 알고리듬(multiplication algorithm)이 알려져 있습니다. 어쨌든, 팩토리얼을 계산하는 것은 단일 곱셈이 아니라 반복된 곱을 포함하므로, 이들 시간 경계가 직접 적용되지 않습니다. 이 설정에서, $n!$을 1에서 $n$까지의 숫자를 순서대로 곱함으로써 계산하는 것은 비효율적인데, 왜냐하면 그것이 $n$ 곱셈을 포함하고, 그 중 상수 분수는 각각 시간 $O(n\log ^{2}n)$를 취하여, 총 시간 $O(n^{2}\log ^{2}n)$를 제공하기 때문입니다. 더 나은 접근 방식은 $i$ 숫자의 수열을 $i/2$ 숫자의 두 부분수열로 분할하고, 각 부분수열을 곱하고, 그 결과를 하나의 마지막 곱셈으로 결합하는 분할-과-정복 알고리듬(divide-and-conquer algorithm)으로 곱셈을 수행하는 것입니다. 팩토리얼에 대한 이 접근 방식은 총 시간 $O(n\log ^{3}n)$을 취합니다: 하나의 로그는 팩토리얼에서 비트의 숫자에서 오고, 두 번째는 곱셈 알고리듬에서 오고, 세 번째는 분할과 정복에서 옵니다.

더 나은 효율성은 제곱에 의한 지수화(exponentiation by squaring)가 지수를 곱으로 확장하는 것보다 빠르다는 원칙에 기초한 그것의 소수 인수분해에서 n!을 계산함으로써 얻습니다. 이를 위한 아놀드 쇤하게(Arnold Schönhage)에 의한 알고리듬은 예를 들어 에라토스테네스의 체(sieve of Eratosthenes)를 사용하여 $n$까지의 소수의 목록을 찾는 것으로 시작하고, 르장드르의 공식을 각 소수에 대해 지수를 계산하기 위해 사용합니다. 그런-다음 그것은 다음과 같이 재귀 알고리듬을 사용하여 이들 지수를 갖는 소수 거듭제곱의 곱을 계산합니다:

• 분할과 정복을 그것의 지수가 홀수인 소수의 곱을 계산하기 위해 사용합니다.
• 모든 지수를 2로 나누고 (정수로 반내림), 이들 더 작은 지수를 갖는 소수 거듭제곱의 곱을 재귀적으로 계산하고, 그 결과를 제곱합니다.
• 이전 두 단계의 결과를 함께 곱합니다.

$n$까지의 모든 소수의 곱은 소수 정리(prime number theorem)에 의해 $O(n)$-비트 숫자이므로, 첫 번째 단계에 대해 시간은 $O(n\log ^{2}n)$이며, 하나의 로그는 분할과 정복에서 오고 또 다른 로그는 곱셈 알고리듬에서 옵니다. 알고리듬에 대한 재귀 호출에서, 소수 정리는 해당하는 곱에서 비트의 숫자가 각 재귀의 수준에서 상수 인수만큼 감소하므로, 모든 재귀의 수준에서 이들 단계에 대해 총 시간은 $O(n\log ^{2}n)$에 기하 급수(geometric series)를 더해짐을 입증하기 위해 다시 호출될 수 있습니다. 두 번째 단계에서 제곱과 세 번째 단계에서 곱셈에 대해 시간은 다시 $O(n\log ^{2}n)$인데, 왜냐하면 각각은 $O(n\log n)$ 비트를 갖는 숫자의 단일 곱셈이기 때문입니다. 다시 말하지만, 각 재귀 수준에서 관련된 숫자는 많은 비트만큼 상수 분수를 가지므로 (왜냐하면 그렇지 않으면 그것들을 반복적으로 제곱하는 것이 너무 큰 최종 결과를 생성할 것이기 때문입니다) 다시 재귀 호출에서 이들 단계에 대해 시간의 총양은 $O(n\log ^{2}n)$에 기하 급수를 더합니다. 결과적으로, 전체 알고리듬은 그것의 결과에서 같은 비트의 숫자를 갖는 단일 곱셈에 비례하는 시간 $O(n\log ^{2}n)$를 취합니다.

Related sequences and functions

Main article: List of factorial and binomial topics

여러 다른 정수 수열은 팩토리얼과 유사하거나 관련이 있습니다:

교대하는 팩토리얼

교대하는 팩토리얼(alternating factorial)은 처음 $n$ 팩토리얼의 교대하는 합: ${\textstyle \sum _{i=1}^{n}(-1)^{n-i}i!}$의 절댓값입니다. 이것들은 주로 그것들의 원시성과 연결에서 연구되어 왔습니다; 오직 그것들의 유한하게 많은 것이 소수일 수 있지만, 이 형식의 소수의 전체 목록은 알려져 있지 않습니다.

바르가바 팩토리얼

바르가바 팩토리얼(Bhargava factorial)은 특별한 경우로 팩토리얼 자체를 포함하여 팩토리얼과 유사한 숫자-이론적 속성을 갖는 만줄 바르가바(Manjul Bhargava)에 의해 정의된 정수 수열의 가족입니다.

두-배 팩토리얼

어떤 홀수 양의 정수 $n$까지의 모든 홀수 정수의 곱은 $n$의 두-배 팩토리얼(double factorial)이라고 불리며, $n!!$에 의해 표시됩니다. 즉, $$(2k-1)!!=\prod _{i=1}^{k}(2i-1)={\frac {(2k)!}{2^{k}k!}}.$$ 예를 들어, 9!! = 1 × 3 × 5 × 7 × 9 = 945. 두-배 팩토리얼은 삼각 적분(trigonometric integrals), 반-정수(half-integer)에서 감마 함수(gamma function)와 초구의 부피(volumes of hyperspheres)에 대해 표현, 이진 트리(binary trees)와 완벽 일치(perfect matching)를 세는 데 사용됩니다.

지수 팩토리얼

삼각형 숫자(triangular number)가 $1$에서 $n$까지의 숫자를 더하고, 팩토리얼이 그것들의 곱을 취하는 것처럼, 지수 팩토리얼은 지수화합니다. $n\$$으로 표시되는 $n$의 지수 팩토리얼은 기본 단계 $0\$=1$와 함께 $n^{(n-1)\$}$로 재귀적으로 정의됩니다. 예를 들어, $$4\$=4^{3^{2^{1}}}=262144.$$ 이들 숫자는 정규 팩토리얼보다 훨씬 더 빠르게 성장합니다.

떨어지는 팩토리얼

표기법 $(x)_{n}$ 또는 $x^{\underline {n}}$는 때때로 $x$를 포함하고 그것까지 세는 $n$ 정수의 곱을 나타내기 위해 사용되며, $x!/(x-n)!$와 같습니다. 이것은 역시 떨어지는 팩토리얼(falling factorial) 또는 역방향 팩토리얼(backward factorial)로 알려져 하고, $(x)_{n}$ 표기법은 포흐하머 기호입니다. 떨어지는 팩토리얼은 $x$ 항목의 우주에서 끌어낼 수 있는 $n$ 구별되는 항목의 서로 다른 수열의 숫자를 셉니다. 그것들은 다항식의 고차 도함수(higher derivative)에서 계수로 발생하고, 확률 변수(random variable)의 팩토리얼 모멘트(factorial moment)에서 발생합니다.

초팩토리얼

$n$의 초팩토리얼(hyperfactorial)은 곱 $1^{1}\cdot 2^{2}\cdots n^{n}$입니다. 이들 숫자는 에르미트 방정식(Hermite polynomials)의 판별식(discriminant)을 형성합니다. 그것들은 K-함수(K-function)에 의해 연속적으로 보간될 수 있고, 스털링의 공식과 윌슨의 정리와 유사합니다.

조르당–폴리야 숫자

조르당–폴리야 숫자(Jordan–Pólya number)는 팩토리얼의 곱이며, 반복을 허용합니다. 모든 각 트리(tree)는 그것의 대칭의 숫자가 조르당–폴리야 숫자인 대칭 그룹(symmetry group)을 가지고, 모든 각 조르당–폴리야 숫자는 일부 트리의 대칭을 셉니니.

프리모리얼

프리모리얼(Primorial) $n\#$은 $n$보다 작거나 같은 소수(prime number)의 곱입니다; 이 구성은 팩토리얼과 일부 유사한 나눔가능성 속성을 제공하지만, 팩토리얼과는 달리 그것들은 제곱-없는(squarefree) 것입니다. 팩토리얼 소수(factorial prime) $n!\pm 1$과 마찬가지로, 연구자들은 프리모리얼 소수(primorial prime) $n\#\pm 1$을 연구해 왔습니다.}}

부분팩토리얼

부분팩토리얼(subfactorial)은 $n$ 대상의 집합의 교란(derangement)의 숫자를 산출합니다. 그것은 때때로 $!n$로 표시되고, $n!/e$에 가장 가까운 정수와 같습니다.}}

초월팩토리얼

$n$의 초월팩토리얼(superfactorial)은 처음 $n$ 팩토리얼의 곱입니다. 초월팩토리얼은 반스 G-함수(Barnes G-function)에 의해 연속적으로 보간됩니다.

External links

• OEIS sequence A000142 (Factorial numbers)
• "Factorial". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
• Weisstein, Eric W. "Factorial". MathWorld.