Interior (topology)

수학(mathematics), 특히 토폴로지(topology)에서, 토폴로지적 공간(topological space) $X$ 의 부분집합(subset) $S$ 의 내부(interior)는 $X$ 에서 열려 있는 $S$ 의 모든 부분집합의 합집합입니다. $S$ 의 내부에 있는 점은 $S$ 의 내부 점(interior point)입니다.

$S$ 의 내부는 $S$ 의 여집합(complement)의 클로저(closure)의 여집합입니다. 이런 의미에서, 내부와 클로저는 이중(dual) 개념입니다.

집합 $S$ 의 외부(exterior)는 $S$ 의 클로저의 여집합입니다; 그것은 집합에 있지도 않고 그것의 경계(boundary)에도 있지 않는 점으로 구성됩니다. 부분집합의 내부, 경계, 및 외부는 함께 전체 공간을 세 개의 블록으로 분할(partition)합니다 (하나 이상이 비어 있을 때 더 작아집니다).

Definitions

Interior point

만약 $S$ 가 유클리드 공간(Euclidean space)의 부분집합이면, $x$ 는 만약 $S$ 에 완전하게 포함되는 $x$ 에 중심을 둔 열린 공(open ball)이 존재하면 $S$ 의 내부 점입니다. (이것은 이 기사의 소개 섹션에 설명되어 있습니다.)

이 정의는 메트릭 $d$ 를 갖는 메트릭 공간(metric space) $X$ 의 임의의 부분집합 $S$ 로 일반화됩니다; $x$ 는 만약 $y$ 가 거리 $d(x,y)<r$ 일 때마다 $S$ 에 있음을 만족하는 $r>0$ 이 존재하면 $S$ 의 내부 점입니다.

이 정의는 "열린 공"을 "열린 집합"으로 대체함으로써 토폴로지적 공간(topological spaces)으로 일반화됩니다. $S$ 를 토폴로지적 공간 $X$ 의 부분집합이라고 놓습니다. 그런-다음 $x$ 는 만약 $x$ 가 $S$ 에 완전하게 포함된 $X$ 의 열린 부분집합에 포함되면 $S$ 의 내부 점입니다. (동등하게, $x$ 는 만약 $S$ 가 $x$ 의 이웃(neighbourhood)이면 $S$ 의 내부 점입니다.)

Interior of a set

토폴로지적 공간 $X$ 의 부분집합 $S$ 의 내부는, $\operatorname {Int} S$ 또는 $\operatorname {int} S$ 또는 $S^{\circ }$ 로 표시되며, 다음 동등한 방법 중 임의의 하나로 정의될 수 있습니다:

$Int S$ 는 $S$ 에 (부분집합으로) 포함된 가장 큰 $X$ 의 열린 부분집합입니다.
$Int S$ 는 $S$ 에 포함된 $X$ 의 모든 열린 집합의 합집합입니다.
$Int S$ 는 $S$ 의 모든 내부 점의 집합입니다.

Examples

a

is an interior point of

M

, because there is an ε-neighbourhood of a which is a subset of

M

.

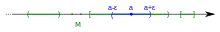
임의의 공간에서, 빈 집합의 내부는 빈 집합입니다.
임의의 공간 $X$ 에서, 만약 $S\subseteq X$ 이면, $\operatorname {int} S\subseteq S$ 입니다.
만약 $X$ (표준 토폴로지를 갖는) 실수 직선(real line) $\mathbb {R}$ 이면, $int([0, 1]) = (0, 1)$ 입니다.
만약 $X$ 가 실수 직선 $\mathbb {R}$ 이면, 유리수(rational numbers)의 집합 $\mathbb {Q}$ 의 내부는 빈 것입니다.
만약 $X$ 가 복소 평면(complex plane) $\mathbb {C}$ 이면, $\operatorname {int} (\{z\in \mathbb {C} :|z|\leq 1\})=\{z\in \mathbb {C} :|z|<1\}$ 입니다.
임의의 유클리드 공간에서, 임의의 유한 집합(finite set)의 내부는 빈 집합입니다.

실수(real numbers)의 집합 위에, 우리는 표준 토폴로지가 아닌 다른 토폴로지를 넣을 수 있습니다:

만약 $X$ 가 아래쪽 극한 토폴로지(lower limit topology)를 갖는 실수 $\mathbb {R}$ 이면, $int([0, 1]) = [0, 1)$ 입니다.
만약 우리가 $\mathbb {R}$ 위에 모든 각 집합이 열린 것인 토폴로지를 고려하면, $int([0, 1]) = [0, 1]$ 입니다.
만약 우리가 $\mathbb {R}$ 위에 열린 집합이 빈 집합과 $\mathbb {R}$ 자체인 토폴로지를 고려하면, $int([0, 1])$ 은 빈 집합입니다.

이들 예제는 집합의 내부가 놓여있는 공간의 토폴로지에 따라 다르다는 것을 보여줍니다. 마지막 두 예제는 다음의 특수한 경우입니다.

임의의 이산 공간(discrete space)에서, 모든 각 집합이 열린 것이기 때문에, 모든 각 집합은 그것의 내부와 같습니다.
임의의 비-이산 공간(indiscrete space) $X$ 에서, 유일한 열린 집합은 빈 집합과 $X$ 자체이기 때문에, $\operatorname {int} X=X$ 이고 $X$ 의 모든 각 적절한 부분집합(proper subset) $S$ 에 대해 $\operatorname {int} S$ 는 빈 집합입니다.

Properties

$X$ 를 토폴로지적 공간으로 놓고 $S$ 와 $T$ 를 $X$ 의 부분집합으로 놓습니다.

$\operatorname {int} S$ 는 $X$ 에서 열린(open) 것입니다.
만약 $T$ 가 $X$ 에서 열린 것이면 $T\subseteq S$ 인 것과 $T\subseteq \operatorname {int} S$ 는 필요충분 조건입니다.
$\operatorname {int} S$ 는 $S$ 가 부분공간 토폴로지(subspace topology)로 주어질 때 $S$ 의 열린 부분집합입니다.
$S$ 가 $X$ 의 열린 부분집합인 것과 $\operatorname {int} S=S$ 인 것은 필요충분(if and only if) 조건입니다.
집중(Intensive): $\operatorname {int} S\subseteq S.$
거듭상등(Idempotence): $\operatorname {int} (\operatorname {int} S)=\operatorname {int} S.$
이항 교집합에 걸쳐 보존/분배(Preserves/distributes over binary intersection): $\operatorname {int} (S\cap T)=(\operatorname {int} S)\cap (\operatorname {int} T).$ $\operatorname {int} (S\cap T)=(\operatorname {int} S)\cap (\operatorname {int} T).$
- 어쨌든, 내부 연산자는 합집합에 걸쳐 분배하지 않는데 왜냐하면 유일한 $\operatorname {int} (S\cup T)~\supseteq ~(\operatorname {int} S)\cup (\operatorname {int} T)$ 가 일반적으로 보장되고 상등이 유지되지 않을 수 있습니다.^{[note 1]} 예를 들어, 만약 $X=\mathbb {R} ,S=(-\infty ,0],$ 및 $T=(0,\infty )$ 이면, $(\operatorname {int} S)\cup (\operatorname {int} T)=(-\infty ,0)\cup (0,\infty )=\mathbb {R} \setminus \{0\}$ 는 $\operatorname {int} (S\cup T)=\operatorname {int} \mathbb {R} =\mathbb {R}$ 의 적절한 부분집합입니다.
$\subseteq$ 에 관해 단조적/비-감소(Monotone/nondecreasing with respect to $\subseteq$ ): 만약 $S\subseteq T$ 이면 $\operatorname {int} S\subseteq \operatorname {int} T$ 입니다.

다른 속성은 다음을 포함합니다:

만약 $S$ 가 $X$ 에서 닫혀 있고 $\operatorname {int} T=\varnothing$ 이면 $\operatorname {int} (S\cup T)=\operatorname {int} S$ 입니다.

Relationship with closure

위의 명제는 만약 다음 기호/단어의 모든 사례가

"interior", "int", "open", "subset", and "largest"

각각 다음으로 대체되면 참으로 남을 것입니다:

"closure", "cl", "closed", "superset", and "smallest"

그리고 다음 기호가 바뀝니다:

" $\subseteq$ "는 " $\supseteq$ "으로 바뀝니다.
" $\cup$ "는 " $\cap$ "으로 바뀝니다.

이 문제에 대한 자세한 내용에 대해, 아래 내부 연산자(interior operator) 또는 쿠라토프스키 클로저 공리(Kuratowski closure axioms) 문서를 참조하십시오.

Interior operator

내부 연산자(interior operator) $\operatorname {int} _{X}$ 는 클로저(closure) 연산자와 이중적이며, 이는 다음이라는 의미에서 $\operatorname {cl} _{X}$ 또는 윗줄 ^—에 의해 표시됩니다: $\operatorname {int} _{X}S=X\setminus {\overline {(X\setminus S)}}$ 그리고 역시 다음에 의해 표시됩니다: ${\overline {S}}=X\setminus \operatorname {int} _{X}(X\setminus S),$ 여기서 $X$ 는 $S$ 를 포함하는 토폴로지적 공간(topological space)이고 백슬래시 $\,\setminus \,$ 는 집합-이론적 차이(set-theoretic difference)를 나타냅니다. 그러므로, 클로저 연산자의 추상 이론과 쿠라토프스키 클로저 공리(Kuratowski closure axioms)는 $X$ 에서 집합을 그것들의 여집합으로 대체함으로써 내부 연산자의 언어로 쉽게 번역될 수 있습니다.

일반적으로, 내부 연산자는 합집합과 교환하지 않습니다. 어쨌든, 완비 메트릭 공간(complete metric space)에서, 다음 결과가 유지됩니다:

Theorem^[1] (C. Ursescu) — $S_{1},S_{2},\ldots$ 를 완비 메트릭 공간 $X$ 의 부분집합의 수열이라고 놓습니다.

만약 각 $S_{i}$ 가 $X$ 에서 닫힌 것이면, $\operatorname {cl} _{X}\left(\bigcup _{i\in \mathbb {N} }\operatorname {int} _{X}S_{i}\right)=\operatorname {cl} _{X}\operatorname {int} _{X}\left(\bigcup _{i\in \mathbb {N} }S_{i}\right).$
만약 각 $S_{i}$ 가 $X$ 에서 열린 것이면, $\operatorname {int} _{X}\left(\bigcap _{i\in \mathbb {N} }\operatorname {cl} _{X}S_{i}\right)=\operatorname {int} _{X}\operatorname {cl} _{X}\left(\bigcap _{i\in \mathbb {N} }S_{i}\right).$

위의 결과는 모든 각 완비 메트릭 공간이 베르 공간(Baire space)임을 의미합니다.

Exterior of a set

토폴로지적 공간 $X$ 의 부분집합 $S$ 의 외부(exterior)는, $\operatorname {ext} _{X}S$ 또는 간단히 $\operatorname {ext} S$ 에 의해 표시되며, $S$ 와 서로소(disjoint)인 가장 큰 열린 집합입니다. 즉, 그것은 $S$ 와 서로소인 $X$ 에서 모든 열린 집합의 합집합입니다. 외부는 여집합의 내부이며, 이는 클로저의 여집합과 같습니다; 다음 공식에서, $\operatorname {ext} S=\operatorname {int} (X\setminus S)=X\setminus {\overline {S}}.$

유사하게, 내부는 여집합의 외부입니다: $\operatorname {int} S=\operatorname {ext} (X\setminus S).$

집합 $S$ 의 내부, 경계(boundary), 및 외부는 함께 전체 공간을 세 개의 블록으로 분할(partition)합니다 (또는 이들 중 하나 이상이 빈 것일 때 더 작습니다): $X=\operatorname {int} S\cup \partial S\cup \operatorname {ext} S,$ 여기서 $\partial S$ 는 $S$ 의 경계를 나타냅니다. 내부와 외부는 항상 열린(open) 것이고, 반면에 경계는 닫힌(closed) 것입니다.

외부 연산자의 속성 중 일부는 내부 연산자의 속성과 다릅니다:

외부 연산자는 포함을 뒤집습니다; 만약 $S\subseteq T$ 이면, $\operatorname {ext} T\subseteq \operatorname {ext} S$ 입니다.
외부 연산자는 거듭-상등(idempotent)이 아닙니다. 그것은 $\operatorname {int} S\subseteq \operatorname {ext} \left(\operatorname {ext} S\right)$ 이라는 속성을 가집니다.

Interior-disjoint shapes

The red shapes are not interior-disjoint with the blue Triangle. The green and the yellow shapes are interior-disjoint with the blue Triangle, but only the yellow shape is entirely disjoint from the blue Triangle.

두 모양 $a$ 와 $b$ 는 만약 그것들 내부의 교집합이 빈 것이면 내부-서로소(interior-disjoint)입니다. 내부-서로소 모양은 그것들의 경계에서 교차하거나 교차하지 않을 수 있습니다.

References

^ Zalinescu, C (2002). Convex analysis in general vector spaces. River Edge, N.J. London: World Scientific. p. 33. ISBN 981-238-067-1. OCLC 285163112.

^ The analogous identity for the closure operator is $\operatorname {cl} (S\cup T)=(\operatorname {cl} S)\cup (\operatorname {cl} T).$ These identities may be remembered with the following mnemonic. Just as the intersection $\cap$ of two open sets is open, so too does the interior operator distribute over intersections $\cap ;$ explicitly: $\operatorname {int} (S\cap T)=(\operatorname {int} S)\cap (\operatorname {int} T).$ And similarly, just as the union $\cup$ of two closed sets is closed, so too does the closure operator distribute over unions $\cup ;$ explicitly: $\operatorname {cl} (S\cup T)=(\operatorname {cl} S)\cup (\operatorname {cl} T).$

Bibliography

Bourbaki, Nicolas (1989) [1966]. General Topology: Chapters 1–4 [Topologie Générale]. Éléments de mathématique. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC 18588129.
Dixmier, Jacques (1984). General Topology. Undergraduate Texts in Mathematics. Translated by Berberian, S. K. New York: Springer-Verlag. ISBN 978-0-387-90972-1. OCLC 10277303.
Császár, Ákos (1978). General topology. Translated by Császár, Klára. Bristol England: Adam Hilger Ltd. ISBN 0-85274-275-4. OCLC 4146011.
Dugundji, James (1966). Topology. Boston: Allyn and Bacon. ISBN 978-0-697-06889-7. OCLC 395340485.
Joshi, K. D. (1983). Introduction to General Topology. New York: John Wiley and Sons Ltd. ISBN 978-0-85226-444-7. OCLC 9218750.
Kelley, John L. (1975). General Topology. Graduate Texts in Mathematics. Vol. 27. New York: Springer Science & Business Media. ISBN 978-0-387-90125-1. OCLC 338047.
Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
Schubert, Horst (1968). Topology. London: Macdonald & Co. ISBN 978-0-356-02077-8. OCLC 463753.
Wilansky, Albert (17 October 2008) [1970]. Topology for Analysis. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-46903-4. OCLC 227923899.
Willard, Stephen (2004) [1970]. General Topology (First ed.). Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.

External links

Interior at PlanetMath.org.

[Zalinescu_2002_p._33-2] Zalinescu, C (2002). Convex analysis in general vector spaces. River Edge, N.J. London: World Scientific. p. 33. ISBN 981-238-067-1. OCLC 285163112.

[mnemonicInteriorAndIntersection-1] The analogous identity for the closure operator is $\operatorname {cl} (S\cup T)=(\operatorname {cl} S)\cup (\operatorname {cl} T).$ These identities may be remembered with the following mnemonic. Just as the intersection $\cap$ of two open sets is open, so too does the interior operator distribute over intersections $\cap ;$ explicitly: $\operatorname {int} (S\cap T)=(\operatorname {int} S)\cap (\operatorname {int} T).$ And similarly, just as the union $\cup$ of two closed sets is closed, so too does the closure operator distribute over unions $\cup ;$ explicitly: $\operatorname {cl} (S\cup T)=(\operatorname {cl} S)\cup (\operatorname {cl} T).$

[note 1]

[1]