Number theory

Original article: w:Number theory

For the book by André Weil, see Number theory: an approach through history; from Hammurapi to Legendre.

Not to be confused with Numerology.

The distribution of prime numbers is a central point of study in number theory. This Ulam spiral serves to illustrate it, hinting, in particular, at the conditional independence between being prime and being a value of certain quadratic polynomials.

숫자 이론(Number theory 또는 이전 사용법에서 산술(arithmetic) 또는 고차 산술(higher arithmetic))은 주로 정수(integer)와 정수-값 함수(integer-valued functions)의 연구에 전념하는 순수 수학(pure mathematics)의 한 가지입니다. 독일 수학자 카를 프리드리히 가우스(Carl Friedrich Gauss) (1777–1855)는 "수학은 과학의 여왕이고 숫자 이론은 수학의 여왕이다"라고 말했습니다. 숫자 이론가들은 정수로 만들어진 수학적 대상 (예를 들어, 유리수(rational number)) 또는 정수의 일반화로 정의된 대상 (예를 들어, 대수적 정수(algebraic integer))의 속성뿐만 아니라 소수(prime number)를 연구합니다.

정수는 그 자체로 또는 방정식 (디오판토스 기하학(Diophantine geometry))에 대한 해로 고려될 수 있습니다. 숫자 이론에서 문제는 일부 방식 (해석적 숫자 이론(analytic number theory))에서 정수, 소수, 또는 다른 숫자-이론적 대상의 속성을 인코딩하는 해석적(analytical) 대상 (예를 들어, 리만 제타 함수(Riemann zeta function))의 연구를 통해 종종 가장 잘 이해됩니다. 우리는 역시, 예를 들어, 후자 (디오판토스 근사(Diophantine approximation))에 의해 근사화될 때, 유리수와 관련하여 실수(real number)를 연구할 수 있습니다.

숫자 이론에 대해 더 오래된 용어는 산술(arithmetic)입니다. 20세기 초까지, 그것은 "숫자 이론"으로 대체되어 왔습니다. (단어 "산술(arithmetic)"은 일반 대중에 의해 "기본 계산(elementary calculations)"을 의미하기 위해 사용됩니다; 그것은 역시 페아노 산술(Peano arithmetic)과 같이 수학적 논리와 부동-점 산술(floating-point arithmetic)과 같이 컴퓨터 과학(computer science)에서 다른 의미를 획득해 왔습니다.) 숫자 이론에 대해 산술이라는 용어의 사용은 20세기 후반에 어느 정도 근거를 되찾았는데, 이는 틀림없이 부분적으로 프랑스의 영향으로 인한 것입니다. 특히, 산술적(arithmetical )은 공통적으로 숫자-이론적(number-theoretic)에 대한 형용사로 선호됩니다.

History

Origins

Dawn of arithmetic

The Plimpton 322 tablet

산술적 본성의 가장 초기의 역사적 발견은 테이블의 한 조각입니다: 부서진 점토 태블릿 Plimpton 322 (Larsa, Mesopotamia, ca. 1800 BC)에는 "피타고라스 세-쌍", 즉, $a^{2}+b^{2}=c^{2}$임을 만족하는 정수 $(a,b,c)$의 목록을 포함하고 있습니다. 세-쌍은 무차별 대입(brute force)에 의해 얻기에는 너무 많고 너무 큽니다. 처음 열의 머리글은 다음과 같습니다: "The takiltum of the diagonal which has been subtracted such that the width..."

테이블의 레이아웃은 그것이 현대 언어에서 다음 항등식(identity)에 어느 정도의 수단에 의해 구성되었음을 시사합니다:

$\left({\frac {1}{2}}\left(x-{\frac {1}{x}}\right)\right)^{2}+1=\left({\frac {1}{2}}\left(x+{\frac {1}{x}}\right)\right)^{2},$

이는 일상적인 고대 바빌로니아 연습 문제에 내포되어 있습니다. 만약 어떤 다른 방법이 사용되었으면, 세-쌍이 먼저 구성되고 그런-다음 $c/a$에 의해 재정렬되었으며, 예를 들어, 응용에 대한 보기와 같이 "테이블"로 실제 사용하기 위한 것 같습니다.

이들 응용이 무엇인지 또는 어떤 것이라도 있을 수 있었는지 여부는 알려져 있지 않습니다; 예를 들어, 바빌로니아의 천문학은 나중에야 진정으로 그 진가를 발휘하게 되었습니다. 그것은 대신 그 테이블이 학교 문제에 대한 수치적 예제의 출처라고 제안되어 왔습니다.

바빌로니아 숫자 이론—또는 이렇게 불릴 수 있는 바빌로니아 수학에서 살아남은 것—이 이 단일, 놀라운 부서진 조각으로 구성되어 있고, 반면 ("대수학"의 중등 학교 의미에서) 바빌로니아 대수학은 예외적으로 잘 발달되었습니다. 후기 네오플라톤 출처는 피타고라스(Pythagoras)가 바빌로니아인들로부터 수학을 배웠다고 말합니다. 훨씬 더 이른 출처에 따르면 탈레스(Thales)와 피타고라스는 이집트에서 여행하고 공부했습니다.

유클리드(Euclid) IX 21–34는 아마도 피타고라스-학파일 것입니다; 그것은 매우 단순한 자료이지만 ("홀수 곱하기 짝수는 짝수", "만약 홀수가 짝수를 측정하면[=나누면], 그것은 역시 그것의 절반을 측정합니다[=나눕니다]"), 그것은 ${\sqrt {2}}$가 무리수(irrational)임을 증명하는 데 필요한 전부입니다. 피타고라스-학파 신비주의자들(Pythagorean mystics)은 홀수와 짝수에 큰 중요성을 부여했습니다. ${\sqrt {2}}$가 무리수라는 발견은 초기 피타고라스-학파 (테오도루스-이전)에 의해 인정되었습니다. (현대적 용어로) 숫자가 무리수일 수 있다는 것을 드러냄으로써, 이 발견은 수학 역사에서 최초의 토대적인 위기를 불러일으킨 것 같습니다; 그것의 증명이나 누설은 때때로 피타고라스 종파에서 추방되거나 분리되었던 히파주스(Hippasus)로 공인됩니다. 이것은 숫자 (정수와 유리수—산술의 주제)와, 다른 한편으로, 길이와 비율 (유리수인지 아닌지에 관계없이 실수로 식별할 수 있음) 사이의 구분을 강제했습니다.

피타고라스-학파 전통은 역시 소위 다각형적(polygonal) 또는 도형적 숫자(figurate numbers)에 대해 말했습니다. 제곱 숫자(square numbers), 세제곱 숫자(cubic numbers), 등은 지금 삼각 숫자(triangular numbers), 오각 숫자(pentagonal numbers), 등에 비해 더 자연스러워 보이지만, 삼각 숫자와 오각 숫자의 합에 대한 연구는 근대 초기 (17세기에서 19세기 초)에 유익한 것으로 판명되었습니다.

우리는 고대 이집트나 베다(Vedic)의 출처에 명확한 산술적 자료는, 비록 각각에 약간의 대수가 있을지라도, 없다는 것을 알고 있습니다. 중국의 나머지 정리(Chinese remainder theorem)는 Sunzi Suanjing (CE 3, 4 또는 5세기)에서 연습으로 나타납니다. (손자의 해에서 한 가지 중요한 단계가 있습니다: 그것은 나중에 아리아바타(Āryabhaṭa)의 Kuṭṭaka에 의해 해결된 문제입니다 – 아래 참조).

중국 수학에도 약간의 수치적 신비주의가 있지만, 피타고라스-학파의 것과는 달리 아무 데도 이끌지 못한 것 같습니다. 피타고라스의 완전 숫자(perfect numbers)처럼, 마방진(magic squares)도 미신에서 오락으로 넘어왔습니다.

Classical Greece and the early Hellenistic period

Further information: Ancient Greek mathematics

몇 가지 단편을 제외하고, 고전 그리스의 수학은 현대 비-수학자의 보고서를 통해 또는 초기 헬레니즘 시대(Hellenistic period)에서 수학적 연구를 통해 우리에게 알려져 있습니다. 숫자 이론의 경우에서, 이것은 대체로 각각 플라톤(Plato)과 유클리드(Euclid)를 의미합니다.

아시아의 수학이 그리스와 헬레니즘 학습에 영향을 미쳤지만, 그리스 수학도 토착 전통인 경우인 것 같습니다.

Eusebius, PE X, chapter 4 mentions of Pythagoras:

"실제로 말한 피타고라스는, 각 민족의 지혜를 부지런히 연구하던 중에, 동방 박사와 승려들의 가르침을 받아 바빌론과 이집트와 온 페르시아를 두루 다녔고, 이 외에도 바라문 밑에서 공부한 것으로 전해집니다 (이들은 인도의 철학자들입니다); 그리고 어떤 사람에게서는 점성술을, 어떤 사람에게서는 기하학을, 다른 사람에게서는 산술과 음악을, 다른 나라에서는 여러 가지를 얻었고, 지혜의 결핍과 부족함에 단단히 결부된 그리스의 현인들에게서만 얻은 것이 없었습니다: 그와 반대로 그는 해외에서 습득한 학식을 그리스인들에게 가르치는 저자가 되었습니다."

아리스토텔레스는 플라톤의 철학이 피타고라스-학파의 가르침을 밀접하게 따랐다고 주장했고, 키케로는 이 주장을 되풀이합니다: Platonem ferunt didicisse Pythagorea omnia ("그들은 플라톤이 피타고라스의 모든 것을 배웠다고 말합니다").

플라톤은 수학에 관심이 많았고 산술과 계산 사이를 명확하게 구분했습니다. (산술에 의해, 그는 부분적으로 산술이나 숫자 이론이 의미하는 바가 아니라 숫자에 대한 이론화를 의미했습니다.) 플라톤의 대화—즉, 테아이테토스(Theaetetus)—중 하나를 통해 우리는 테오도루스(Theodorus)가 ${\sqrt {3}},{\sqrt {5}},\dots ,{\sqrt {17}}$가 무리수임을 입증했음을 압니다. 테아이테토스는 플라톤처럼 테오도루스의 제자였습니다; 그는 서로 다른 종류의 비-정수-비율-가능(incommensurables)을 구별하는 것을 연구했고, 따라서 틀림없이 숫자 시스템(number systems)의 연구의 선구자였습니다. (유클리드의 원론(Euclid's Elements)의 책 X는 파푸스(Pappus)에 의해 주로 테아이테토스의 연구에 기반한 것으로 설명됩니다.)

유클리드는 그의 원론의 일부를 소수와 나눔가능성, 명백히 숫자 이론에 속하고 숫자 이론에 기본이 되는 주제에 할애했습니다 (유클리드의 원론의 책 VII에서 IX). 특히, 그는 두 숫자의 최대 공통 약수를 계산하는 데 알고리듬 (유클리드 알고리듬(Euclidean algorithm); 원론, 제안. VII.2)과 소수의 무한성(infinitude of primes)에 대한 최초의 알려진 증명 (원론, 제안. IX.20)을 제공했습니다.

1773년, 레싱(Lessing)은 사서로 일하면서 원고에서 발견한 경구(epigram)를 출판했습니다; 그것은 아르키메데스(Archimedes)가 에라토스테네스(Eratosthenes)에게 보낸 편지라고 주장했습니다. 에피그램은 아르키메데스의 가축 문제(Archimedes's cattle problem)로 알려지게 된 것을 제안했습니다; 그 해 (원고에 없음)는 불확정 이차 방정식 (나중에 이름이 잘못 지정된 펠의 방정식(Pell's equation)으로 축소됨)을 해결해야 합니다. 우리가 아는 한, 그러한 방정식은 인도 학파(Indian school)에서 처음으로 성공적으로 다루어졌습니다. 아르키메데스 자신이 해결 방법을 가지고 있었는지 여부는 알려져 있지 않습니다.

Diophantus

Title page of the 1621 edition of Diophantus's Arithmetica, translated into Latin by Claude Gaspard Bachet de Méziriac.

알렉산드리아의 디오판토스에 대해서는 알려진 바가 거의 없습니다; 그는 아마도 기원후 3세기, 즉 유클리드 이후 약 500년 후에 살았을 것입니다. 디오판토스의 Arithmetica의 13권 중 6권은 원래 그리스어로 남아 있고 그 외 4권은 아랍어 번역본으로 남아 있습니다. Arithmetica는 보통 $f(x,y)=z^{2}$ 또는 $f(x,y,z)=w^{2}$ 형식의 다항 방정식의 시스템에 대한 유리 해를 찾는 것이 임무인 해결된 문제의 모음입니다. 따라서, 오늘날, 우리는 유리수 또는 정수 해를 찾아야 하는 다항 방정식을 말할 때 Diophantine equations이라고 말합니다.

디오판토스는 곡선과 대수적 다양체(algebraic varieties)에서 좌표가 유리수인 점을 연구하고 있었다고 말할 수 있습니다; 어쨌든, 지금 우리가 기하학 용어로 기본 대수학이라고 부르는 것을 수행했던 고전 시대의 그리스인과 달리, 디오판토스는 오늘날 우리가 순수 대수적 용어로 기본 대수적 기하학이라고 부르는 것을 수행했습니다. 현대 언어에서 디오판토스가 한 일은 다양체의 유리 매개변수화를 찾는 것이었습니다; 즉, (말하자면) $f(x_{1},x_{2},x_{3})=0$ 형식의 방정식이 주어지면, 그의 목표는 (본질적으로) $r$과 $s$의 모든 값에 대해, $i=1,2,3$에 대해 $x_{i}=g_{i}(r,s)$를 설정하는 것이 $f(x_{1},x_{2},x_{3})=0$에 대한 해를 제공함을 만족하는 세 개의 유리 함수(rational functions) $g_{1},g_{2},g_{3}$를 찾는 것이었습니다.

디오판토스는 유리 매개변수화가 불가능한 일부 비-유리 곡선의 방정식도 연구했습니다. 그는 접선 구성에 해당하는 것을 수단으로 이들 곡선 (타원 곡선(elliptic curves), 처음으로 알려진 발생으로 보이는 것)에서 몇 가지 유리 점을 찾을 수 있었습니다: 좌표 기하학으로 변환된 (이는 디오판토스 시대에는 존재하지 않았습니다), 그의 방법은 알려진 유리 점에서 곡선에 대한 접선을 그리고, 그런-다음 접선과 곡선의 다른 교차점을 찾는 것으로 시각화됩니다; 그 다른 점은 새로운 유리 점입니다. (디오판토스는 역시 가름선 구성의 특수한 경우라고 불릴 수 있는 것에 의지했습니다.)

디오판토스는 주로 유리 해에 관심을 두었지만, 그는 정수에 대한 일부 결과, 특히 모든 각 정수는 네 개의 제곱의 합이라고 가정했습니다 (비록 그가 그렇게 많이 명시적으로 언급하지는 않았지만).

Āryabhaṭa, Brahmagupta, Bhāskara

그리스 천문학은 아마도 삼각법(trigonometry)을 도입할 정도로, 인도 학습에 영향을 미쳤을지 모르지만, 그렇지 않으면 인도 수학은 토착 전통인 것 같습니다. 특히, 유클리드의 원론은 18세기 이전에 인도에 전파되었다는 증거는 없습니다.

아리아바타 (기원후 476–550년)는 $n\equiv a_{1}{\bmod {m}}_{1}$, $n\equiv a_{2}{\bmod {m}}_{2}$의 동시 합동 쌍이 그가 kuṭṭaka, 또는 pulveriser라고 부르는 방법에 의해 해결될 수 있음을 보여주었습니다; 이것은 아마도 인도에서 독립적으로 발견된 유클리드 알고리듬(의 일반화)에 가까운 절차입니다. 아리아바타는 천문학적 계산에 대한 응용을 염두에 두고 있었던 것 같습니다.

브라마굽타 (기원후 628년)는 부정 이차 방정식—특히, 아르키메데스가 처음으로 관심을 가졌을 수 있고. 페르마와 오일러의 시대까지 서양에서 풀기 시작하지 않았던 잘못된 이름-지은 펠 방정식(Pell equation)에 대한 시스템적인 연구를 시작했습니다. 나중에, 산스크리트어 저자들은 브라마굽타의 기술 용어를 사용하여 그 뒤를 따랐을 것입니다. 펠의 방정식을 풀기 위한 일반적인 절차 (차크라발라(chakravala) 또는 "순환 방법")는 마침내 자이야데바(Jayadeva)에 의해 발견되었습니다(11세기에 인용됨; 그렇지 않으면 그의 연구는 손실됩니다); 가장 오래 살아남은 설명은 바스카라 2세(Bhāskara II)의 Bīja-gaṇita (12세기)에 나타납니다.

인도 수학은 18세기 후반까지 유럽에서 거의 알려지지 않았습니다; 브라마굽타와 바스카라의 연구는 1817년 헨리 콜브룩(Henry Colebrooke)에 의해 영어로 번역되었습니다.

Arithmetic in the Islamic golden age

Further information: Mathematics in medieval Islam and Islamic Golden Age

Al-Haytham as seen by the West: on the frontispiece of Selenographia Alhasen [sic] represents knowledge through reason and Galileo knowledge through the senses.

9세기 초, 칼리프 알 마문(Al-Ma'mun)은 많은 그리스 수학 연구와 적어도 하나의 산스크리트 연구 (브라마굽타의 Brāhmasphuṭasiddhānta일 수도 있고 아닐 수도 있는 Sindhind)의 번역을 명령했습니다. 디오판토스의 주요 연구, Arithmetica는 쿠스타 이븐 루카(Qusta ibn Luqa, 820–912)에 의해 아랍어로 번역되었습니다. 논문 al-Fakhri (알-칼라지(al-Karajī)가 지음, 953 – 약 1029)의 일부는 어느 정도 그것을 기반으로 합니다. 라시드 루쉬디(Rashed Roshdi)에 따르면, 알-카라지와 동시대인 이븐 알-하이삼(Ibn al-Haytham)은 나중에 윌슨의 정리(Wilson's theorem)라고 불리게 되는 것을 알고 있었습니다.

Western Europe in the Middle Ages

북 아프리카와 콘스탄티노플을 여행하고 공부한 피보나치(Fibonacci)에 의한 산술 진행에서 제곱에 관한 논문을 제외하고, 중세 서유럽에서는 숫자 이론에 대해 언급할 만한 것이 없었습니다. 그리스 고대 연구에 대한 새로운 연구 덕분에 르네상스(Renaissance) 후기에 유럽에서 상황이 바뀌기 시작했습니다. 촉매는 디오판토스의 Arithmetica의 텍스트 교정과 라틴어로의 번역이었습니다.

Early modern number theory

Fermat

Pierre de Fermat

피에르 드 페르마(Pierre de Fermat, 607–1665년)는 자신의 글을 출판한 적이 없습니다; 특히, 숫자 이론에 대한 그의 연구는 수학자에게 보낸 편지와 개인적인 여백 메모에 거의 전적으로 포함되어 있습니다. 그의 메모와 편지에서, 그는 임의의 증명을 거의 쓰지 않았습니다 - 그는 그 영역에 수학적 설명을 하지 않았습니다.

평생 동안 페르마는 이 분야에 다음과 같은 공헌을 했습니다:

• 페르마의 첫 번째 관심사 중 하나는 완전 숫자(perfect numbers, 유클리드의 원론 IX에 나타남)와 친화 숫자(amicable numbers)였습니다; 이들 주제로 인해 그는 정수 약수(divisors)에 대해 연구하게 되었으며, 이는 처음부터 당시의 수학적 공동체와 접촉할 수 있었던 서신 (1636년 이후)의 주제 중 하나였습니다.
• 1638년 페르마는 모든 자연수는 네 개의 제곱 또는 더 작은 것의 합으로 나타낼 수 있다고, 증명 없이, 주장했습니다.
• 페르마의 작은 정리(Fermat's little theorem, 1640): 만약 a가 소수 p로 나누어지지 않으면, $a^{p-1}\equiv 1{\bmod {p}}$입니다.
• 만약 a와 b가 서로소(coprime)이면, $a^{2}+b^{2}$는 −1 모듈로 4와 합동인 임의의 소수로 나누어지지 않습니다; 그리고 1 모듈로 4에 합동인 모든 각 소수는 $a^{2}+b^{2}$ 형식으로 쓸 수 있습니다. 이들 두 명제 역시 1640년으로 거슬러 올라갑니다; 1659년에, 페르마는 하위헌스에게 무한 하강의 방법(method of infinite descent)으로 후자의 명제를 증명했다고 말했습니다.
• 1657년, 페르마는 $x^{2}-Ny^{2}=1$을 푸는 문제를 영국 수학자에게 도전 과제로 제시했습니다. 그 문제는 월리스(Wallis)와 브롱커(Brouncker)에 의해 몇 달 만에 해결되었습니다. 페르마는 그들의 해가 유효하다고 생각했지만, 그들이 증명 없이 알고리듬을 제공했다고 지적했습니다 (페르마는 이를 인식하지 못했지만 Jayadeva와 Bhaskara가 그랬던 것처럼). 그는 무한 하강으로 증명을 찾을 수 있다고 말했습니다.
• 페르마는 Observations on Diophantus (Obs. XLV)의 부록에서 $x^{4}+y^{4}=z^{4}$가 정수에서 비-자명한 해를 가지지 않는다는 것을 말하고 (무한 하강에 의해) 입증했습니다. 페르마는 역시 그의 서신에서 $x^{3}+y^{3}=z^{3}$은 비-자명한 해를 가지지 않고, 이것은 역시 무한 하강에 의해 입증될 수 있다고 언급했습니다. 최초의 알려진 증명은 오일러(Euler, 1753; 실제로 무한 하강에 의해)에 기인한 것입니다.
• 페르마는 모든 $n\geq 3$에 대해 $x^{n}+y^{n}=z^{n}$에 대한 해가 없음 (페르마의 마지막 정리)을 보여주었다고 주장했습니다. 이 주장은 그의 디오판토스의 복사본 여백에 있는 그의 주석에 나타납니다.

Euler

Leonhard Euler

숫자 이론에서 레온하르트 오일러(Leonhard Euler, 1707–1783)의 관심은, 1729년 그의 친구인 아마추어 골드바흐(Goldbach)가 그 주제에 대한 페르마의 연구 일부를 그에게 지적하면서 처음 박차를 가했습니다. 이것은 그 주제에 대해 동시대인들의 관심을 끌지 못한 페르마의 상대적인 성공 이후, 현대 숫자 이론의 "재탄생"이라고 불렸습니다. 숫자 이론에 대한 오일러의 연구는 다음을 포함합니다:

• 페르마의 명제에 대한 증명. 여기에는 페르마의 작은 정리(Fermat's little theorem)를 포함합니다 (오일러에 의해 비-소수 모듈러스로 일반화됩니다); $p=x^{2}+y^{2}$인 것과 $p\equiv 1{\bmod {4}}$인 것은 필요충분 조건이라는 사실; 모든 각 정수가 네 개의 제곱의 합이라는 증명을 위한 초기 연구 (최초의 완전한 증명은 조제프-루이 라그랑주(Joseph-Louis Lagrange, 1770)에 의해 이루어졌으며, 곧 오일러 자신이 개선했습니다); $x^{4}+y^{4}=z^{2}$에 대한 비-영 정수 해의 결핍 (페르마의 마지막 정리의 경우 n=4, 오일러도 관련된 방법으로 입증했던 경우 n=3을 암시합니다).
• 펠의 방정식(Pell's equation), 오일러에 의해 처음으로 잘못된 이름이 지정되었습니다. 그는 연속 분수와 펠의 방정식 사이의 연결에 대해 썼습니다.
• 해석적 숫자 이론을 향한 첫 걸음. 네 개의 제곱의 합, 분할(partitions), 오각 숫자(pentagonal numbers), 및 소수의 분포(distribution)에 대한 그의 연구에서, 오일러는 숫자 이론에서 해석학으로 볼 수 있는 것 (특히 무한 급수)의 사용을 개척했습니다. 그는 복소 해석학(complex analysis)의 발달 이전에 살았기 때문에 그의 연구 대부분은 거듭제곱 급수(power series)의 형식적 조작에 국한되어 있습니다. 그는, 어쨌든, 나중에 리만 제타 함수(Riemann zeta function)라고 불리는 것에 대해 매우 주목할 만한 (완전히 엄격하지는 않지만) 초기 연구를 수행했습니다.
• 이차 형식. 페르마의 주도에 따라, 오일러는 어떤 소수가 $x^{2}+Ny^{2}$의 형식으로 표현될 수 있는지에 대한 추가 연구를 수행했으며, 그 중 일부는 이차 상호관계(quadratic reciprocity)를 예시했습니다.
• 디오판토스 방정식. 오일러는 지너스 0과 1의 일부 디오판토스 방정식에 대해 연구했습니다. 특히, 그는 디오판토스의 연구를 연구했습니다; 그는 그것을 시스템화하려고 노력했지만, 아직 그러한 노력을 기울일 때가 아니었습니다—대수적 기하학은 아직 초기 단계였습니다. 그는 디오판토스 문제와 그가 직접 연구를 시작한 타원 적분(elliptic integrals) 사이에 연관성이 있음을 알아차렸습니다.

"Here was a problem, that I, a 10 year old, could understand, and I knew from that moment that I would never let it go. I had to solve it." – Sir Andrew Wiles about his proof of Fermat's Last Theorem.

Lagrange, Legendre, and Gauss

Carl Friedrich Gauss's Disquisitiones Arithmeticae, first edition

조제프-루이 라그랑주(Joseph-Louis Lagrange, 1736–1813)는 페르마와 오일러의 연구와 관찰 중 일부에 대한 완전한 증명을 처음으로 제공했습니다—예를 들어, 네-제곱 정리(four-square theorem)와 잘못-이름-지은 "펠 방정식"의 기본 이론 (알고리듬 해결책은 페르마와 그의 동시대 사람들과 역시 그들 이전의 자이야데바와 바스카라 2세에 의해 발견되었습니다.) 그는 역시 완전한 일반성 ($mX^{2}+nY^{2}$와 반대)으로 이차 형식(quadratic forms)을 연구했습니다—그것들의 동치 관계를 정의하고, 축소된 형식으로 표시하는 방법, 등을 보여주었습니다.

아드리앵-마리 르장드르(Adrien-Marie Legendre, 1752–1833)는 이차 상호관계의 법칙을 처음으로 언급했습니다. 그는 역시 소수 정리(prime number theorem)와 산술 진행에 대한 디리클레의 정리(Dirichlet's theorem on arithmetic progressions)에 해당하는 것이 무엇인지 추측했습니다. 그는 방정식 $ax^{2}+by^{2}+cz^{2}=0$을 완전히 다루었고 나중에 가우스에 의해 완전히 개발된 선을 따라 이차 형식을 연구했습니다. 노년기에, 그는 $n=5$에 대한 페르마의 마지막 정리를 처음으로 입증했습니다 (페터 구스타프 르죈 디리클레(Peter Gustav Lejeune Dirichlet)에 의해 연구가 완료되고, 그와 소피 제르맹(Sophie Germain) 모두에게 공을 돌렸습니다).

Carl Friedrich Gauss

그의 Disquisitiones Arithmeticae (1798)에서 카를 프리드리히 가우스 (1777–1855)는 이차 상호관계(quadratic reciprocity)의 법칙을 입증했고 이차 형식의 이론을 개발했습니다 (특히, 그 구성을 정의했습니다). 그는 역시 몇 가지 기본 표기법 (합동)을 소개하고 소수성 테스트를 포함한 계산적 문제에 대한 섹션을 할애했습니다. Disquisitiones의 마지막 섹션은 단위의 근(roots of unity)와 숫자 이론 사이의 연결 고리를 설립했습니다:

원의 분할의 이론은...섹션 7에서 다루는 것은 그 자체로 산술에 속하지 않지만 그 원리는 고급 산술에서만 이끌어낼 수 있습니다.

이러한 방법에서, 가우스는 틀림없이 에바리스트 갈루아(Évariste Galois)의 연구와 대수적 숫자 이론 모두에 첫 진출을 했습니다.

Maturity and division into subfields

Ernst Kummer

Peter Gustav Lejeune Dirichlet

19세기 초부터, 다음과 같은 발전이 점차 일어났습니다:

• 연구 분야로서 숫자 이론 (또는 고급 산술(higher arithmetic))의 자체-자각 상승.
• 기본 현대 숫자 이론에 필요한 현대 수학의 많은 발전: 복소 해석학(complex analysis), 그룹 이론(group theory), 갈루아 이론(Galois theory)—대수학의 해석과 추상화에서 더 엄격함을 동반합니다.
• 숫자 이론을 현대 하위-분야—특히, 해석적 및 대수적 숫자 이론으로 대략적으로 세분합니다.

대수적 숫자 이론은 상호관계와 순환론(cyclotomy)에 대한 연구로 시작되었다고 말할 수 있지만, 추상 대수학(abstract algebra) 및 초기 아이디얼 이론과 평가(valuation) 이론의 발전과 함께 진정으로 진가를 발휘했습니다. 아래를 참조하십시오. 해석적 숫자 이론의 전통적인 출발점은 산술 진행에 대한 디리클레의 정리(Dirichlet's theorem on arithmetic progressions 1837)이며, 그의 증명은 L-함수(L-functions)를 도입했고 일부 점근적 해석과 실수 변수에 대한 극한하는 과정을 포함합니다. 숫자 이론에서 해석적 아이디어의 첫 번째 사용은 형식적 거듭제곱 급수와 비-엄격한 (또는 암시적) 극한하는 논증을 사용했던 오일러 (1730년대)로 거슬러 올라갑니다. 숫자 이론에서 복소 해석학의 사용은 나중에 나옵니다: 제타 함수에 대한 베른하르트 리만(Bernhard Riemann, 1859)의 연구가 정식의 시작 점입니다; 야코비의 네-제곱 정리(Jacobi's four-square theorem, 1839)는 그것보다 앞선 것으로, 지금까지 해석적 숫자 이론 (모듈러 형식)에서 주도적인 역할을 한 처음에는 다른 가닥에 속합니다.

각 하위-필드의 역사는 아래 해당 섹션에서 간략하게 설명합니다; 보다 완전한 처리를 위해 각 하위-필드의 주요 기사를 참조하십시오. 각 영역에서 가장 흥미로운 질문 중 많은 부분이 열려 있고 적극적으로 연구 중입니다.

Main subdivisions

Elementary number theory

용어 기본(elementary)은 일반적으로 복소 해석학(complex analysis)을 사용하지 않는 방법을 나타냅니다. 예를 들어, 소수 정리(prime number theorem)는 1896년에 복소 해석학을 사용하여 처음으로 증명되었지만, 기본 증명은 1949년에야 에르되시(Erdős)와 셀베르그(Selberg)에 의해 발견되었습니다. 그 용어는 다소 모호합니다: 예를 들어 복소 타우버 정리(Tauberian theorems)에 기반한 증명 (예를 들어, 위너–이케하라)은 종종 상당히 계몽적인 것으로 고려되지만 이를테면 복소 해석 자체보다는 푸리에 해석(Fourier analysis)을 사용함에도 불구하고 기본적이지 않습니다. 다른 곳과 마찬가지로, 기본 증명은 비-기본적인 것보다 대부분의 독자에게 더 길고 어려울 수 있습니다.

Number theorists Paul Erdős and Terence Tao in 1985, when Erdős was 72 and Tao was 10.

숫자 이론은 그 결과 중 많은 부분이 비전문가에게 설명될 수 있는 분야라는 명성을 가지고 있습니다. 동시에, 이들 결과의 증명은 특별히 접근하기 어려운데, 부분적으로 왜냐하면 그들이 사용하는 도구의 범위가 수학 내에서 비정상적으로 광범위하기 때문입니다.

Analytic number theory

Main article: Analytic number theory

Riemann zeta function ζ(s) in the complex plane. The color of a point s gives the value of ζ(s): dark colors denote values close to zero and hue gives the value's argument.

The action of the modular group on the upper half plane. The region in grey is the standard fundamental domain.

해석적 숫자 이론은 다음과 같이 정의될 수 있습니다:

• 도구 측면에서, 실수(real)와 복소(complex) 해석학의 도구를 수단으로 정수를 연구합니다; 또는
• 그것의 관심의 관점에서, 항등식과 반대되는 크기와 밀도에 대한 추정의 숫자 이론 내 연구.

일반적으로 해석적 숫자 이론의 일부로 고려되는 일부 주제, 예를 들어, 체 이론(sieve theory)은 첫 번째 정의보다 두 번째 정의에서 더 잘 다룹니다: 예를 들어 일부 체 이론은 해석학을 거의 사용하지 않지만, 해석적 숫자 이론에 속합니다.

다음은 해석적 숫자 이론의 문제 예시입니다: 소수 정리(prime number theorem), 골드바흐 추측 (또는 쌍둥이 소수 추측, 또는 하디-리틀우드 추측(Hardy-Littlewood conjectures)), 워링의 문제(Waring problem) 및 리만 가설(Riemann hypothesis). 해석적 숫자 이론의 가장 중요한 도구 중 일부는 원 방법(circle method), 체 방법(sieve methods) 및 L-함수 (또는 그 속성에 대한 연구)입니다. 모듈러 형식(mododular form) (및, 더 일반적으로, 자기동형 형식(automorphic forms)) 이론은 역시 해석적 숫자 이론의 도구 상자에서 점점 더 중심적인 위치를 차지합니다.

우리는 대수적 숫자(algebraic numbers)에 대한 해석적 질문을 할 수 있고, 그러한 질문에 답하기 위해 해석적 수단을 사용할 수 있습니다; 따라서 대수적 숫자 이론과 해석적 숫자 이론이 교차합니다. 예를 들어, 우리는 소수 아이디얼 (대수적 숫자의 분야에서 소수의 일반화)을 정의하고 특정 크기까지 몇 개의 소수 아이디얼이 있는지 물어볼 수 있습니다. 이 질문은 주제의 뿌리에 있는 핵심 해석적 대상, 리만 제타 함수(Riemann zeta function)의 일반화인 데데킨트 제타 함수(Dedekind zeta functions)의 조사를 수단으로 답을 얻을 수 있습니다. 이것은 적절하게 구성된 복소-값 함수의 해석적 동작에서 수열(sequence, 여기서, 소수 아이디얼 또는 소수)의 분포에 대한 정보를 도출하는 해석적 숫자 이론의 일반적인 절차의 예시입니다.

Algebraic number theory

Main article: Algebraic number theory

대수적 숫자(algebraic number)는 유리수 계수를 갖는 일부 다항 방정식 $f(x)=0$에 대한 해인 복소수입니다; 예를 들어, (말하자면) $x^{5}+(11/2)x^{3}-7x^{2}+9=0$의 모든 각 해 $x$는 대수적 숫자입니다. 대수적 숫자의 필드는 대수적 숫자 필드(algebraic number fields), 또는 간단히 숫자 필드(number fields)라고도 불립니다. 대수적 숫자 이론은 대수적 필드를 연구합니다. 따라서, 해석적 숫자 이론과 대수적 숫자 이론은 중첩될 수 있고 중첩됩니다: 전자는 그 방법에 의해 정의되고 후자는 연구의 대상에 의해 정의됩니다.

Disquisitiones arithmeticae에서 이차 형식에 대한 논의가 이차 필드에서 아이디얼(ideals)과 노름(norms)의 관점에서 다시 언급될 수 있기 때문에, 가장 단순한 종류의 숫자 필드 (즉, 이차 필드)는 가우스에 의해 이미 연구되었다고 주장할 수 있습니다. (이차 필드는 $a+b{\sqrt {d}}$ 형식의 모든 숫자로 구성되며, 여기서 $a$와 $b$는 유리수이고 $d$는 제곱근이 유리수가 아닌 고정된 유리수입니다.) 그 점에 대해, 11-세기 차크라발라 방법(chakravala method)은—현대 용어에서—실수 이차 숫자 필드의 단위를 찾기 위한 알고리듬에 해당합니다. 어쨌든, 바스카라도 가우스도 이를테면 숫자 필드에 대해 알지 못했습니다.

우리가 알고 있는 주제의 근거는 아이디얼 숫자(ideal numbers), 아이디얼의 이론(theory of ideals), 평가 이론(valuation theory)이 개발되었던 때 19세기 후반에 설정되었습니다; 이것들은 대수적 숫자 필드에서 고유한 인수분해의 부족을 처리하는 세 가지 보완적인 방법입니다. (예를 들어, 유리수와 ${\sqrt {-5}}$에 의해 생성된 필드에서, 숫자 $6$은 $6=2\cdot 3$과 $6=(1+{\sqrt {-5}})(1-{\sqrt {-5}})$로 인수화될 수 있습니다; $2$, $3$, $1+{\sqrt {-5}}$와 $1-{\sqrt {-5}}$의 모두는 기약이고, 따라서, 소박한 의미에서, 정수 중 소수와 유사합니다.) (Kummer에 의한) 아이디얼 숫자의 개발에 대한 초기 추진력은 더 높은 상호관계 법칙, 즉, 이차 상호관계(quadratic reciprocity)의 일반화에 대한 연구에서 비롯된 것 같습니다.

숫자 필드는 종종 더 작은 숫자 필드의 확장으로 연구됩니다; 필드 L은 만약 L이 K를 포함하면 필드 K의 확장이라고 말합니다. (예를 들어, 복소수 C는 실수 R의 확장이고, 실수 R은 는 유리수 Q의 확장입니다.) 주어진 숫자 필드의 가능한 확장을 분류하는 것은 어렵고 부분적으로 열려 있는 문제입니다. 아벨 확장—즉, K에 걸쳐 L의 갈루아 그룹(Galois group) Gal(L/K)가 아벨 그룹(abelian group)임을 만족하는 K의 확장 L—은 상대적으로 잘 알려져 있습니다. 그것들의 분류는 19세기 후반에 (부분적으로 Kronecker와 Eisenstein에 의해) 시작되었고 1900–1950년에 주로 수행된 클래스 필드 이론(class field theory)의 프로그램의 목적이었습니다.

대수적 숫자 이론에서 활발한 연구 분야의 예제는 이와사와 이론(Iwasawa theory)입니다. 현재 주요 수학 연구 계획 중 하나, 랭글랜즈 프로그램(Langlands program)은 때때로 클래스 필드 이론을 숫자 필드의 비-아벨 확장으로 일반화하려는 시도로 설명됩니다.

Diophantine geometry

Main article: Diophantine geometry

디오판토스 기하학(Diophantine geometry)의 중심 문제는 디오판토스 방정식이 해를 가질 때, 그리고 해가 있다면 얼마나 많은지를 결정하는 것입니다. 취한 접근 방식은 방정식의 해를 기하학적 대상으로 생각하는 것입니다.

예를 들어, 두 변수에서 방정식은 평면에서 곡선을 정의합니다. 보다 일반적으로, 둘 이상의 변수에서 방정식 또는 방정식의 시스템은 곡선(curve), 표면(surface) 또는 n-차원 공간에서 다른 그러한 대상을 정의합니다. 디오판토스 기하학에서, 곡선이나 표면에 유리 점(rational points, 그것의 모든 좌표가 유리수인 점) 또는 정수 점(integral points, 그것의 모든 좌표가 정수인 점)이 있는지 묻습니다. 만약 임의의 그러한 점이 있으면, 다음 단계는 그것이 몇 개인지, 어떻게 분배되는지 묻는 것입니다. 이러한 방향에서 기본적인 질문은 주어진 곡선 (또는 표면)에 유리 점이 유한하게 또는 무한히 많이 있는지 여부입니다.

피타고라스 방정식(Pythagorean equation) $x^{2}+y^{2}=1$에서, 우리는 그것의 유리 해, 즉, $x$와 $y$가 둘 다 유리수임을 만족하는 해 $(x,y)$에 대해 연구하고 싶습니다. 이것은 $a^{2}+b^{2}=c^{2}$에 대한 모든 정수 해를 묻는 것과 같습니다; 후자의 방정식에 대한 임의의 해는 전자에 대한 해 $x=a/c$, $y=b/c$를 제공합니다. 그것은 역시 $x^{2}+y^{2}=1$에 의해 기술된 곡선에서 유리 좌표를 갖는 모든 점에 대해 묻는 것과 같습니다. (이 곡선은 원점을 중심으로 반지름 1의 원으로 발생합니다.)

Two examples of an elliptic curve, that is, a curve of genus 1 having at least one rational point. (Either graph can be seen as a slice of a torus in four-dimensional space.)

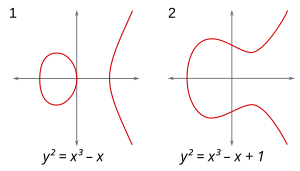
그는 방정식에 대한 질문을 곡선 위의 점으로 바꾸어 표현한 것이 좋은 것으로 판명되었습니다. 대수적 곡선 위의 유리수 또는 정수 점의 숫자의 유한한지 아닌지—즉, $f$가 두 변수에서 다항식인 방정식 $f(x,y)=0$에 대한 유리수 또는 정수 해—는 결정적으로 곡선의 지너스에 의존하는 것으로 밝혀졌습니다. 지너스는 다음과 같이 정의될 수 있습니다: $f(x,y)=0$에서 변수를 복소수로 허용합니다; 그런-다음 $f(x,y)=0$은 (투영) 4-차원 공간에서 2-차원 표면을 정의합니다 (왜냐하면 두 개의 복소수 변수가 4개의 실수 변수, 즉, 4차원으로 분해될 수 있기 때문입니다). 만약 우리가 표면에 있는 (도넛) 구멍의 수를 세면; 우리는 이 숫자를 $f(x,y)=0$의 지너스라고 부릅니다. 다른 기하학적 개념도 똑같이 중요한 것으로 밝혀졌습니다.

역시 디오판토스 근사(Diophantine approximations)의 밀접하게 연결된 영역이 있습니다: 숫자 $x$가 주어지면, 그런-다음 유리수로 얼마나 잘 근사할 수 있는지 찾는 것입니다. (우리는 유리수를 작성하는 데 걸리는 공간의 양에 비해 적절한 근사를 찾고 있습니다. $|x-a/q|<{\frac {1}{q^{c}}}$이면 $x$에 대한 좋은 근사 ($\gcd(a,q)=1$를 갖는) $a/q$라고 부르며, 여기서 $c$는 큽니다.) 이 질문은 $x$가 대수적 숫자이면 특히 중요합니다. 만약 $x$가 잘 근사화될 수 없으면, 일부 방정식은 정수 또는 유리수 해를 가지지 않습니다. 더욱이, 몇 가지 개념 (특히 높이의 개념)은 디오판토스 기하학과 디오판토스 근사 연구 모두에서 매우 중요한 것으로 밝혀졌습니다. 이 질문은 역시 초월적 숫자 이론(transcendental number theory)의 특별한 관심 대상입니다: 만약 어떤 숫자가 임의의 대수적 숫자보다 더 잘 근사화될 수 있으면, 그것은 초월적 숫자(transcendental number)입니다. 이 논증에 의해 π와 e가 초월적인 것으로 나타났습니다.

디오판토스 기하학은 대수적 숫자 이론의 특정 질문에 답하는 데 그래픽 방법 모음인 숫자의 기하학(geometry of numbers)과 혼동되어서는 안 됩니다. 어쨌든 산술적 기하학(Arithmetic geometry)은 디오판토스 기하학(Diophantine geometry)이라는 용어가 다루는 것과 거의 같은 영역에 대한 현대 용어입니다. 산술적 기하학(arithmetic geometry)이라는 용어는 디오판토스 근사의 기법보다는 현대 (예를 들어 팔팅스의 정리(Faltings's theorem)에서와 같이) 대수적 기하학과의 연결을 강조하고자 할 때 가장 자주 사용됩니다.

Other subfields

아래의 영역은 더 오래된 자료를 기반으로 하더라도 20세기 중반부터 시작됩니다. 예를 들어, 아래에서 설명하는 것처럼, 숫자 이론에서 알고리듬의 문제는 매우 오래되었으며, 어떤 의미에서는 증명의 개념보다 오래되었습니다; 동시에 계산-가능성(computability)에 대한 현대 연구는 1930년대와 1940년대에, 계산적 복잡성 이론(computational complexity theory)은 1970년대부터 시작되었습니다.

Probabilistic number theory

Main article: Probabilistic number theory

확률론적 숫자 이론의 대부분은 서로 독립(independent)은 아니지만 거의 독립적인 변수의 연구의 중요한 특수 사례로 볼 수 있습니다. 예를 들어, 1에서 100만 사이의 임의의 정수가 2로 나누어지는 사건과 3으로 나누어지는 사건은 거의 독립적이지만 완전하지는 않습니다.

확률론적 조합론(probabilistic combinatorics)은 $0$보다 큰 확률로 발생하는 모든 일이 때때로 발생해야 한다는 사실을 사용한다고 때때로 말합니다; 확률론적 숫자 이론의 많은 응용이 특이한 것은 무엇이든 드물어야 한다는 사실에 달려 있다고 동등한 정의로 말할 수 있습니다. 만약 특정 대수적 대상 (말하자면, 특정 방정식에 대한 유리수 또는 정수 해)가 현명하게 정의된 특정 분포의 꼬리에 있는 것으로 표시될 수 있으면, 그들 중 몇 개만 있어야 함을 따릅니다; 이것은 확률적 명제에 뒤따르는 매우 구체적인 비-확률론적 명제입니다.

때때로, 비-엄격한 확률론적 접근 방식은 많은 휴리스틱(heuristic) 알고리듬과 열린 문제, 특히 크라메르의 추측(Cramér's conjecture)으로 이어집니다.

Arithmetic combinatorics

Main articles: Arithmetic combinatorics and Additive number theory

만약 우리가 상당히 "두꺼운" 무한 집합(infinite set) $A$에서 시작하면, 산술 진행: 말하자면 $a$, $a+b,a+2b,a+3b,\ldots ,a+10b$에서 많은 원소가 포함되어 있습니까? 큰 정수를 $A$의 원소의 합으로 쓸 수 있어야 합니까?

이들 질문은 산술 조합론(arithmetic combinatorics)의 특징입니다. 이것은 현재 합체되고 있는 분야입니다; 그것은 덧셈 숫자 이론(additive number theory, 이는 소수나 제곱수와 같은 산술적 의미의 특정 매우 특정한 집합 $A$와 자체를 관련시킴)과, 틀림없이, 일부 급속히 발전하는 새로운 자료와 함께 일부 숫자의 기하학(geometry of numbers)을 포함합니다. 성장과 분포의 문제에 초점을 맞추는 것은 부분적으로 에르고딕 이론(ergodic theory), 유한 그룹 이론(finite group theory), 모델 이론(model theory) 및 기타 분야와의 발전적인 연결을 설명합니다. 덧셈 조합론(additive combinatorics)이라는 용어도 사용됩니다; 어쨌든, 연구 중인 집합 $A$는 정수의 집합일 필요는 없지만, 전통적으로 덧셈 기호가 아닌 곱셈 기호가 사용되는 비-교환 그룹(groups)의 부분집합일 필요가 있습니다; 그것들은 역시 $A+A$와 $A$·$A$의 성장이 비교될 수 있는 경우에서 링(rings)의 부분집합일 수 있습니다.

Computational number theory

Main article: Computational number theory

A Lehmer sieve, a primitive digital computer used to find primes and solve simple Diophantine equations.

알고리듬(algorithm)이라는 단어는 알-콰리즈미(al-Khwārizmī)의 특정 독자에게만 거슬러 올라가지만, 해의 주의 깊은 설명은 증명보다 오래되었습니다: 그러한 방법 (즉, 알고리듬)은 인식할 수 있는 임의의 수학—고대 이집트, 바빌로니아, 베다, 중국—만큼이나 오래되었고, 반면에 증명은 고전 시대의 그리스인들에게만 나타났습니다.

초기 사례는 우리가 현재 유클리드 알고리듬이라고 부르는 것입니다. 그것의 기본 형식 (즉, 최대 공통 약수를 계산하기 위한 알고리듬)에서, 그것은 정확성의 증명과 함께 원론에서 책 VII의 제안 2로 나타납니다. 어쨌든, 숫자 이론에서 자주 사용되는 형식 (즉, 방정식 $ax+by=c$에 대한 정수 해를 찾기 위한 알고리듬, 또는, 중국 나머지 정리에 의해 존재가 보장되는 양을 찾기 위한 알고리듬)에서, 그것은 아리아바타(Āryabhaṭaa, 기원후 5-6세기)의 연구에 kuṭṭaka ("pulveriser")라는 알고리듬으로 처음 등장하지만, 정확성에 대한 증명은 없습니다. 두 가지 주요 질문이 있습니다: "우리가 이것을 계산할 수 있습니까?" "우리가 그것을 빠르게 계산할 수 있습니까?" 누구나 숫자가 소수인지 여부를 테스트할 수 있고, 그렇지 않으면, 그것을 소수로 나눌 수 있습니다; 빠르게 그렇게 하는 것은 또 다른 문제입니다. 우리는 이제 소수성을 테스트(testing primality)하기 위한 빠른 알고리듬을 알고 있지만, 많은 연구 (이론적 및 실제적 둘 다)에도 불구하고 인수화를 위해 진정으로 빠른 알고리듬은 없습니다.

계산의 어려움은 유용할 수 있습니다: 메시지 암호화 (예를 들어, RSA)를 위한 최신 프로토콜은 모두에게 알려진 기능에 의존하지만 그 역은 선택된 소수에게만 알려져 있고 자체로 계산하는 데 너무 오랜 시간이 걸립니다. 예를 들어, 이들 함수는 만약 특정 큰 정수가 인수화되면 오직 역을 계산할 수 있다는 것일 수 있습니다. 숫자 이론 이외의 많은 어려운 계산 문제가 알려져 있지만 오늘날 작동하는 대부분의 암호화 프로토콜은 몇 가지 숫자 이론 문제의 어려움을 기반으로 합니다.

어떤 것들은 전혀 계산할 수 없을 수도 있습니다; 사실, 이것은 어떤 경우에 입증될 수 있습니다. 예를 들어, 1970년에 힐베르트의 10번째 문제( Hilbert's 10th problem)에 대한 해결책으로 모든 디오판토스 방정식을 풀 수 있는 튜링 기계(Turing machine)는 없다는 것이 입증되었습니다. 특히 이것은 계산-가능하게 열거-가능(computably enumerable) 공리의 집합이 주어지면, 공리에서 시작하여 방정식의 집합이 정수 해를 갖는지 여부에 대한 증명이 없는 디오판토스 방정식이 있음을 의미합니다. (우리는 필연적으로 정수 해가 없는 디오판토스 방정식에 대해 말하고 있을 것인데, 왜냐하면, 적어도 하나의 해를 갖는 디오판토스 방정식이 주어지면, 해 자체가 해가 존재한다는 사실의 증명을 제공하기 때문입니다. 우리는 특정한 디오판토스 방정식이 이런 종류라는 것을 증명할 수 없는데, 왜냐하면 이것은 해가 없다는 것을 의미하기 때문입니다.)

Applications

숫자-이론가 레너드 딕슨(Leonard Dickson, 1874–1954)은 "숫자 이론이 임의의 응용으로도 더럽혀지지 않은 것을 신에게 감사합니다"라고 말했습니다. 그러한 견해는 숫자 이론에 더 이상 적용할 수 없습니다. 1974년에, 도널드 커누스(Donald Knuth)는 "...기본 숫자 이론에서 거의 모든 각 정리는 컴퓨터가 고속 수치적 계산을 수행하도록 하는 문제와 관련하여 자연스럽고 동기 부여된 방식으로 발생합니다"라고 말했습니다. 기본 숫자 이론은 컴퓨터 과학자를 위한 이산 수학(discrete mathematics) 과정에서 가르칩니다; 다른 한편으로, 숫자 이론은 역시 수치 해석(numerical analysis)에서 연속에 적용됩니다. 암호화(cryptography)에 대한 잘 알려진 응용뿐만 아니라 수학의 다른 많은 영역에 대한 응용도 있습니다.

Prizes

미국 수학 학회는 숫자 이론에서 콜 상(Cole Prize in Number Theory)을 수여합니다. 게다가, 숫자 이론은 페르마 상(Fermat Prize)이 수여하는 세 가지 수학적 하위-분야 중 하나입니다.

See also

• Algebraic function field
• Finite field
• p-adic number

Sources

• This article incorporates material from the Citizendium article "Number theory", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.

Further reading

Two of the most popular introductions to the subject are:

• G.H. Hardy; E.M. Wright (2008) [1938]. An introduction to the theory of numbers (rev. by D.R. Heath-Brown and J.H. Silverman, 6th ed.). Oxford University Press. ISBN 978-0-19-921986-5. Retrieved 2016-03-02.
• Vinogradov, I.M. (2003) [1954]. Elements of Number Theory (reprint of the 1954 ed.). Mineola, NY: Dover Publications.

Hardy and Wright's book is a comprehensive classic, though its clarity sometimes suffers due to the authors' insistence on elementary methods (Apostol n.d.). Vinogradov's main attraction consists in its set of problems, which quickly lead to Vinogradov's own research interests; the text itself is very basic and close to minimal. Other popular first introductions are:

• Ivan M. Niven; Herbert S. Zuckerman; Hugh L. Montgomery (2008) [1960]. An introduction to the theory of numbers (reprint of the 5th edition 1991 ed.). John Wiley & Sons. ISBN 978-81-265-1811-1. Retrieved 2016-02-28.
• Kenneth H. Rosen (2010). Elementary Number Theory (6th ed.). Pearson Education. ISBN 978-0-321-71775-7. Retrieved 2016-02-28.

Popular choices for a second textbook include:

• Borevich, A. I.; Shafarevich, Igor R. (1966). Number theory. Pure and Applied Mathematics. Vol. 20. Boston, MA: Academic Press. ISBN 978-0-12-117850-5. MR 0195803.
• Serre, Jean-Pierre (1996) [1973]. A course in arithmetic. Graduate Texts in Mathematics. Vol. 7. Springer. ISBN 978-0-387-90040-7.

External links

• Media related to Number theory at Wikimedia Commons
• Number Theory entry in the Encyclopedia of Mathematics
• Number Theory Web