Overdetermined system

수학(mathematics)에서, 방정식 시스템(system of equations)은, 만약 미지수보다 많은 방정식이 있으면, 초과-결정된(overdetermined) 것으로 여겨집니다.^[1]^[2]^{[citation needed]} 초과-결정된 시스템은, 임의의 계수로 구성될 때, 거의 항상 불일치된(inconsistent) 것입니다 (그것은 해를 가지지 않습니다). 어쨌든, 초과-결정된 시스템은 일부 경우, 예를 들어 만약 일부 방정식이 시스템에서 여러 번 발생하면, 또는 만약 일부 방정식이 다른 것의 선형 조합(linear combination)이면, 해를 가질 것입니다.

용어는 제약을 세는 것(constraint counting)의 개념의 관점에서 설명될 수 있습니다. 각각의 미지수(unknown)는 이용-가능한 자유도(degree of freedom)로 볼 수 있습니다. 시스템에 도입된 각 방정식은 1 자유도를 제한하는 제약(constraint)으로 보일 수 있습니다. 그러므로 결정적 경우는 방정식의 숫자와 자유 변수의 숫자가 같을 때 발생합니다. 자유도를 제공하는 모든 각 변수에 대해, 해당하는 제약이 존재합니다. 초과-결정된(overdetermined) 경우는 시스템이 초과-제약되면 – 즉, 방정식이 미지수의 숫자보다 많을 때 발생합니다. 대조적으로, 미달-결정된(underdetermined) 경우는 시스템이 미달-제약될 때 – 즉, 방정식의 숫자가 미지수의 숫자보다 적을 때 발생합니다. 그러한 시스템은 보통 해의 무한한 숫자를 가집니다.

Systems of equations

An example in two dimensions

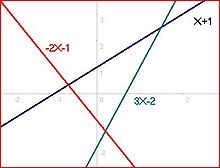
3 방정식과 2 미지수 ( $X$ 와 $Y$ )의 시스템을 생각해 보십시오. 이것은 3>2이기 때문에 초과-결정된 것이고, 다이어그램 #1에 해당합니다:

{\begin{aligned}Y&=-2X-1\\Y&=3X-2\\Y&=X+1.\end{aligned}}

선형 방정식의 각 쌍에 대해 하나의 해가 있습니다: 첫 번째와 두 번째 방정식에 대해 (0.2, −1.4), 첫 번째와 세 번째에 대해 (−2/3, 1/3), 및 두 번째와 세 번째에 대해 (1.5, 2.5)의 해를 가집니다. 어쨌든, 세 개 모두를 동시에 만족시키는 해는 없습니다. 다이어그램 #2와 3은 불일치된 것인 다른 구성을 보여주는데 왜냐하면 직선의 모두 위에 놓인 점이 없기 때문입니다. 이 종류의 시스템은 불일치된(inconsistent) 것으로 생각합니다.

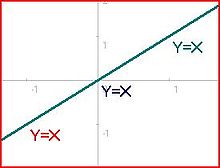
초과-결정된 시스템이 해를 실제로 가지는 유일한 경우는 다이어그램 #4, 5, 및 6에 표시되어 있습니다. 이들 예외는 초과-결정된 시스템이 독립적인 방정식의 숫자가 미지수의 숫자를 초과하지 않는 충분히 선형적 종속(linearly dependent) 방정식을 포함할 때 발생할 수 있습니다. 선형 종속성은 일부 방정식은 다른 방정식을 선형적으로 결합함으로써 얻어질 수 있음을 의미합니다. 예를 들어, Y = X + 1 및 2Y = 2X + 2는 선형적 종속 방정식인데, 왜냐하면 두 번째 것은 두 배의 첫 번째 것을 취함으로써 얻어질 수 있기 때문입니다.

Matrix form

선형 방정식의 임의의 시스템은 행렬(matrix) 방정식으로 쓸 수 있습니다. 방정식의 이전 시스템 (다이어그램 #1)은 다음으로 쓸 수 있습니다:

{\begin{bmatrix}2&1\\-3&1\\-1&1\\\end{bmatrix}}{\begin{bmatrix}X\\Y\\\end{bmatrix}}={\begin{bmatrix}-1\\-2\\1\\\end{bmatrix}}

(방정식에 해당하는) 계수 행렬(coefficient matrix)의 행이 (미지수에 해당하는) 열의 숫자를 초과하는 것에 주목하십시오. 이것은 그 시스템이 초과-결정된 것임을 의미합니다. 이 행렬의 랭크(rank)는 2이며, 이것은 시스템에서 종속 변수(dependent variables)의 숫자에 해당합니다.^[3] 선형 시스템이 일치된 것과 계수 행렬이 증가된 행렬(augmented matrix) (더해진 여분의 열을 가진 계수 행렬(coefficient matrix), 해당 열은 상수의 열 벡터(column vector)입니다)과 같은 랭크를 갖는 것은 필요충분 조건(if and only if)입니다. 증가된 행렬은 랭크 3을 가지므로, 시스템은 불일치된 것입니다. 널러티(nullity)는 0이며, 이것은 널 공간(null space)이 오직 영 벡터를 포함하고 따라서 기저(basis)를 가지지 않음을 의미합니다.

선형 대수(linear algebra)에서, 행 공간(row space), 열 공간(column space) 및 널 공간(null space)의 개념은 행렬의 속성을 결정하는 것에 대해 중요합니다. 위의 제약과 자유도(degrees of freedom)의 비공식 토론은 이들의 보다 공식적인 개념과 직접 관련됩니다.

Homogeneous case

동차 경우 (모든 상수 항이 영인 경우)는 항상 일치된 것입니다 (왜냐하면 자명한 해, 모든-영 해를 가지기 때문입니다). 선형적 종속 방정식의 숫자에 따라 두 가지 경우가 있습니다: 단지 자명한(trivial) 해를 가지는 것, 또는 자명한 해와 다른 해의 무한한 집합이 있는 것입니다.

선형 방정식의 시스템을 생각해 보십시오: 1 ≤ i ≤ M에 대해 L_i = 0, 및 변수 X₁, X₂, ..., X_N, 여기서 각 L_i는 X_i의 가중된 합입니다. 그런 다음 X₁ = X₂ = ... = X_N = 0은 항상 하나의 해입니다. M < N일 때, 시스템이 미달-결정된 것이고 항상 추가 해의 무한대가 있습니다. 사실, 해 공간의 차원은 항상 적어도 N − M입니다.

M ≥ N에 대해, 모든 값이 0이 되는 것 이외의 해는 없을 수 있습니다. 오직 방정식의 시스템이 독립 방정식의 숫자가 최대 N − 1인 충분히 종속성 (선형적 종속 방정식)을 가질 때 다른 해의 무한대가 있을 것입니다. 그러나 M ≥ N와 함께 독립 방정식의 숫자는 N만큼 높을 수 있으며, 이 경우에서 자명한 해는 오직 하나입니다.

Non-homogeneous case

선형 방정식의 시스템에서, 1 ≤ i ≤ M에 대해 L_i=c_i, 변수 X₁, X₂, ..., X_N에서, 방정식은 때때로 선형적 종속입니다; 사실 선형적 독립 방정식의 숫자는 N+1을 절대 초과할 수 없습니다. 우리는 N 미지수와 M 방정식 (M>N)을 가진 초과-결정된 시스템에 대해 다음의 가능한 경우를 가집니다.

M = N+1이고 모든 M 방정식이 선형적 독립(linearly independent)입니다. 이 경우는 해를 산출하지 않습니다. 예를 들어: x = 1, x = 2.
M > N이지만 오직 K 방정식 (K < M 및 K ≤ N+1)이 선형적 독립입니다. 이것의 세 개의 가능한 하위-경우가 존재합니다:
- K = N+1. 이 경우는 해를 산출하지 않습니다. 예제: 2x = 2, x = 1, x = 2.
- K = N. 이 경우는 하나의 해 또는 해 없음 중 하나를 산출하는데, 후자는 하나의 방정식의 계수 벡터가 다른 방정식의 계수 벡터의 가중된 합으로 복제될 수 있지만, 다른 방정식의 상수 항에 적용된 가중된 합이 하나의 방정식의 상수 항을 복제하지 않습니다. 하나의 해를 갖는 예제: 2x = 2, x = 1. 해 없음을 갖는 예제: 2x + 2y = 2, x + y = 1, x + y = 3.
- K < N. 이 경우는 무한하게 많은 해 또는 해 없음 중 하나를 산출하는데, 후자는 이전의 하위-경우에서 처럼 발생합니다. 무한하게 많은 해를 갖는 예제: 3x + 3y = 3, 2x + 2y = 2, x + y = 1. 해 없음을 갖는 예제: 3x + 3y + 3z = 3, 2x + 2y + 2z = 2, x + y + z = 1, x + y + z = 4.

이들 결과는 가우스 소거법(Gaussian elimination)을 사용함으로써 시스템 계수의 증가된 행렬(augmented matrix)을 행 사다리꼴(row echelon)로 배치함으로써 이해하기 더 쉬울 수 있습니다. 이 행 사다리꼴은 주어진 시스템과 동등한 것인 방정식 시스템의 증가된 행렬입니다 (그것은 정확히 같은 해를 가집니다). 시스템이 불일치된 것 (해 없음)과 사다리꼴에서 마지막 비-영 행이 (c가 비-영 상수인 방정식 0 = c를 제공하는) 마지막 열에서 있는 오직 하나의 비-영 엔트리를 가지는 것은 필요충분 조건입니다. 그렇지 않으면, 사다리꼴에서 비-영 행의 개수가 미지수의 숫자와 같을 때 정확히 하나의 해가 있고, 비-영 행의 개수가 변수의 숫자보다 작을 때 무한히 많은 해가 있습니다.

루셰–카펠리 정리(Rouché–Capelli theorem)에 따르면, 그것을 또 다른 식으로 표현하면, 만약 증가된 행렬의 랭크(rank)가 계수 행렬(coefficient matrix)의 랭크보다 더 크면 임의의 방정식 시스템 (초과-결정된 것 또는 다른 것)이 불일치된 것입니다. 만약, 다른 한편으로, 이들 두 행렬의 랭크가 같으면, 시스템은 적어도 하나의 해를 반드시 가집니다. 해가 유일한 것과 랭크가 변수의 숫자와 같은 것은 필요충분 조건입니다. 그렇지 않으면 일반적인 해는 k 자유 매개변수를 가지며 여기서 k는 변수의 개수와 랭크 사이의 차이입니다; 따라서 그러한 경우에서 해의 무한대가 있습니다.

Exact solutions

행렬 대수(matrix algebra)를 사용하여, 모든 정확한 해는 구할 수 있거나, 또는 그것이 존재하지 않음을 보일 수 있습니다. System of linear equations#Matrix solution을 참조하십시오.

Approximate solutions

보통 최소 제곱(ordinary least squares)의 방법은 초과-결정된 시스템에 대한 근사적 해를 찾기 위해 사용될 수 있습니다. 시스템 $Ax=b$ 에 대해, 최소 제곱 공식은 다음 문제로부터 얻습니다:

\min _{x}\Vert Ax-b\Vert ,

정규 방정식(normal equations)과 함께 쓸 수 있는 해는,^[4]

x=(A^{\mathrm {T} }A)^{-1}A^{\mathrm {T} }b,

여기서 ${\mathrm {T} }$ 는 행렬 전치(matrix transpose)를 나타내고, 제공된 $(A^{\mathrm {T} }A)^{-1}$ 는 존재합니다 (즉, 제공된 A는 완전한 열 랭크(column rank)를 가집니다). 이 공식과 함께 근사적 해는 정확한 해가 존재하지 않을 때 찾아지고, 그것은 해가 존재할 때 정확한 해를 제공합니다. 어쨌든, 좋은 수치적 정확도를 성취하기 위해, 최소 제곱 문제를 해결하기 위한 A의 QR 인수분해(QR factorization)를 사용하는 것이 바람직합니다.^[5]

In general use

이 개념은, 다항 방정식의 시스템(systems of polynomial equations) 또는 부분 미분 방정식(partial differential equations)과 같은, 방정식의 보다 일반적인 시스템에 역시 적용될 수 있습니다. 다항 방정식 시스템의 경우에서, 초과-결정된 시스템이 하나의 해를 가지지만, 어떤 방정식도 다른 방정식의 결과가 아니고, 임의의 방정식을 제거할 때 새로운 시스템은 더 많은 해를 가지는 것에서 우연히 발생할 것입니다. 예를 들어, $(x-1)(x-2)=0,(x-1)(x-3)=0$ 은 하나의 해 $x=1$ 를 가지지만, 그 자체로 각 방정식은 두 개의 해를 가집니다.

References

^ "Planet Math, Overdetermined".
^ Gentle. Numerical Linear Algebra for Applications in Statistics.
^ Stevens, Scott A. "System Analysis - Rank and Nullity" (PDF). Math 220 - Matrices Handouts. Pennsylvania State University. Retrieved 3 April 2017.
^ Anton, Howard; Rorres,, Chris (2005). Elementary Linear Algebra (9th ed.). John Wiley and Sons, Inc. ISBN 978-0-471-66959-3.{{cite book}}: CS1 maint: extra punctuation (link)
^ Trefethen, Lloyd; Bau, III, David (1997). Numerical Linear Algebra. ISBN 978-0898713619.

[1] "Planet Math, Overdetermined".

[2] Gentle. Numerical Linear Algebra for Applications in Statistics.

[3] Stevens, Scott A. "System Analysis - Rank and Nullity" (PDF). Math 220 - Matrices Handouts. Pennsylvania State University. Retrieved 3 April 2017.

[4] Anton, Howard; Rorres,, Chris (2005). Elementary Linear Algebra (9th ed.). John Wiley and Sons, Inc. ISBN 978-0-471-66959-3.{{cite book}}: CS1 maint: extra punctuation (link)

[5] Trefethen, Lloyd; Bau, III, David (1997). Numerical Linear Algebra. ISBN 978-0898713619.

[1]

[2]

[3]

[4]

[5]